ある日、数学が苦手なかなちゃんは、
星がかけなくて困っていました。

だああー!
星かけねえええええ
おっ、苦戦してるね!
定規で一筆書きするといいよ。
へー!
やってみよっかなあー
わ!かけた!
でしょでしょ??
じつはね、
数学の問題には、
星形の角度を求める問題
があるんだ。
たとえば、こんな感じ↓↓
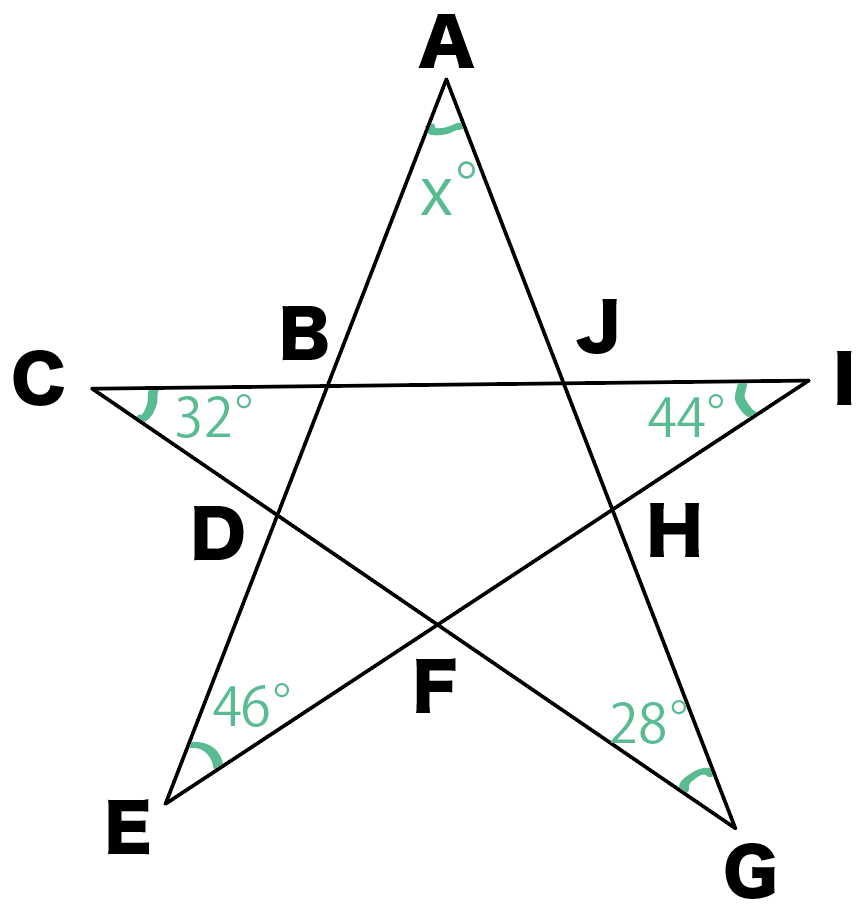
つぎの星形の角度のxを求めなさい。
ひょえー!
雰囲気むずそーー
いや!
基本おさえちゃえば大丈夫。
いっしょにといていこう!
はい!!
星形の角度の求め方はつぎの3ステップだよ。
へー!
3ステップならできそう!
いけるいける!
それじゃあ、
さっきの星形の問題をといていこう。
つぎの星形の角度のxを求めなさい。

星形を、
「3つの三角形」
にわけて考えてみよう。
えっと・・・・
3つ??
そうそう。
星形の中に、
色んな図形が見えてこない??

三角形と….
あっ、
五角形もある!!
そう!
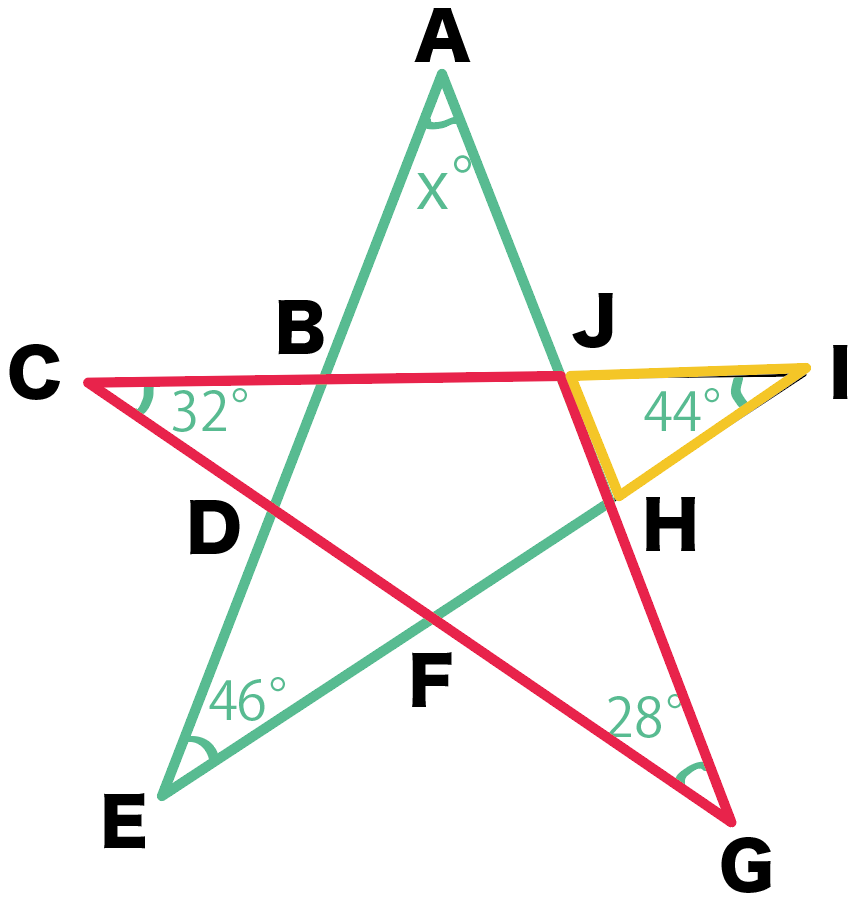
今回は、その中の3つの三角形に注目しよう。
練習問題でいうと、
の3つだね。
ひー
なんでその3つなんだろう?
それはね……
ひ、み、つ
えっ!
外角の定理ってなんだっけ??
っていう人もいると思って、
ちゃんと用意しといたよ!
さ、さすがすぎる!!
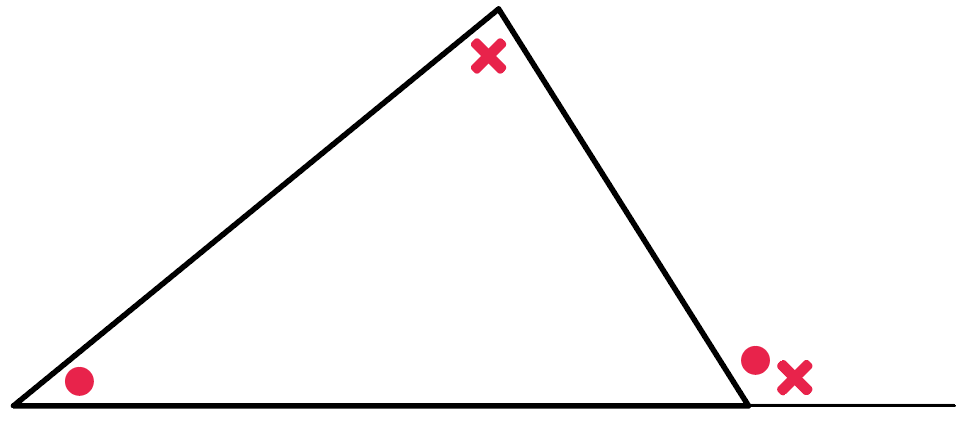
簡単にいうと、
三角形の内角を2つ足すと、
接してない外角になる
ってやつ。
下の図でいうと、
○と×をたしたら、
外角は「○+×」になるってわけ。
ああああああー
思い出してきたようなきがする!
これを星形の中の、
3つの三角形で考えてみよう!
外角になりそうなところ……
あっ、あった!
△AEHの外角は∠JHIだ!
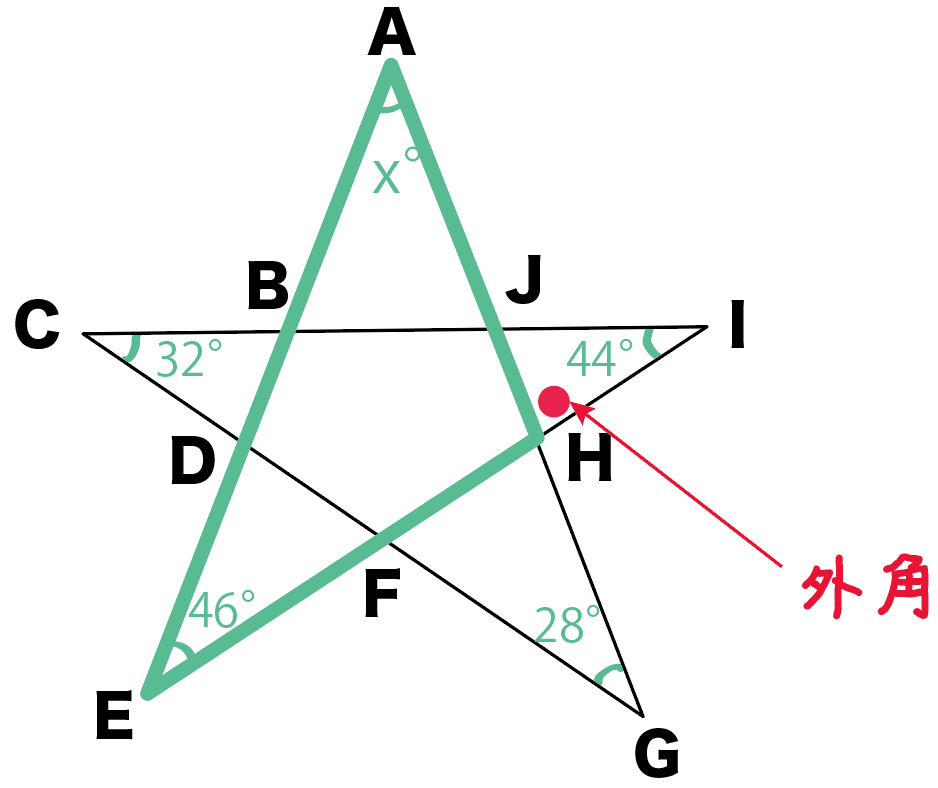
いいね。
△CGJでも同じように考えると……
あっ!
△CGJでいうと、∠HJIが外角になってる!
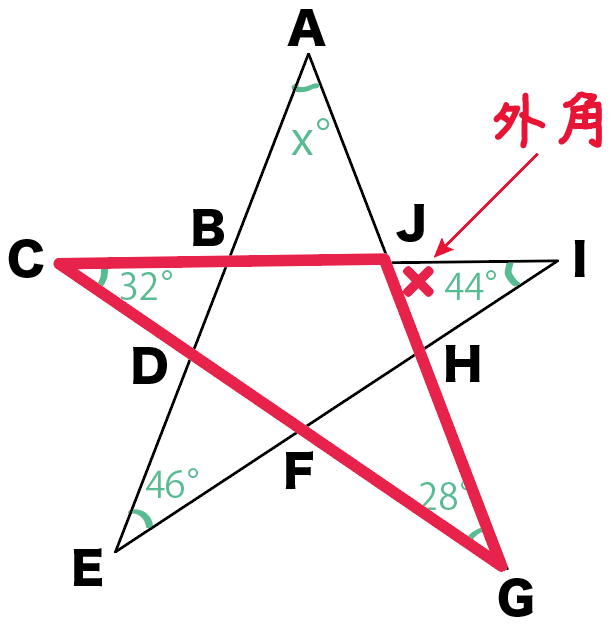
三角形の外角の定理で、
角を移動させるとどうなる??
えっと・・・・、
あっ。
小さい三角形に集まってない!??
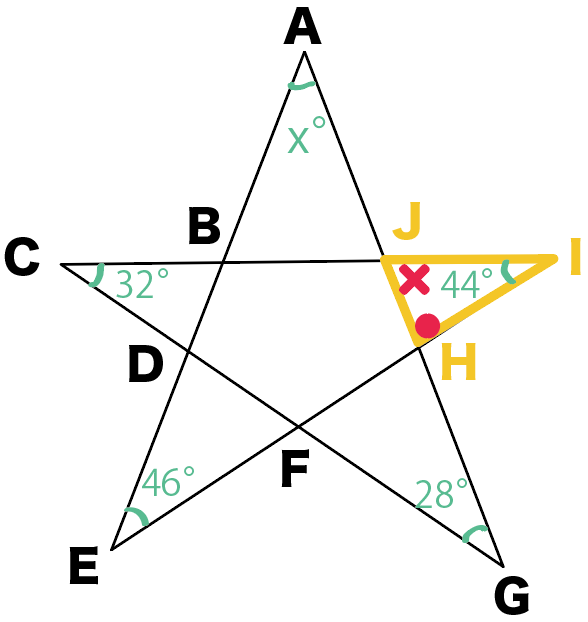
そう!
ぜんぶあわせて三角形の内角になってるね。
ということは??
三角形の内角の和は180度だから、
星の角度の和が180度になるってことだ!!
いいね!
じゃあ、角xはいくつ??
えっと・・・、
三角形の外角の定理をつかうと、
になる。
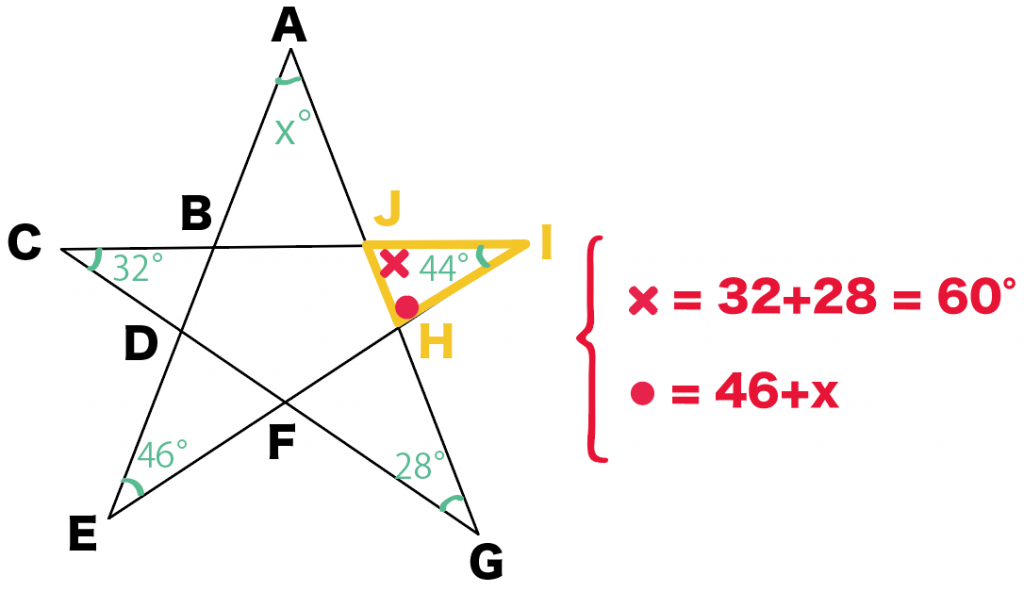
うんうん
だから、△HIJの内角は全部で180度だから、
(46+x) + 60 + 44 = 180
x = 30°
だ!
xは30°!
星形の角度の求め方はどうだったかな?
の3ステップだったね。
これなら、
他の問題も解けそうかも!!
いいね、このことを利用した問題は、
まだまだたくさんあるんだ。
最初はよく分かんなかったけど、
特徴さえわかっちゃえば、分かりやすいね!!
そう!
どんな問題でも、
初めては分かりづらい。
けど、一度理解すれば大丈夫。
色んな問題が解けるようになるよ!
はい!
ありがとうございました!
こんにちは!この記事をかいているKenだよ。本屋がよんでるね。
多角形の対角線の本数の求め方には公式があるよ。
n角形の対角線の本数は、
n(n-3)÷2
で計算できちゃうんだ。
つまり、
(頂点の数)×(頂点の数 – 3)÷ 2
ってことだね。
それじゃあ、
五角形の対角線の本数を求めてみよう。
公式のnに「5」を代入すればいいから、
n(n-3)÷2
= 5×(5-3)÷2
= 5
になるね。
た、たしかに対角線は5本ひけそう。。
す、すごいな。
この公式。
公式はめちゃ便利。
それはわかった。
だけれども、
なぜ多角形の対角線の本数を求められるんだろう??
話がうますぎるよね。
つぎの3ステップで考えると、
公式をつかえる理由がわかるよ。
1つの頂点から何本の対角線がひけるか
を考えてみよう。
まず、
隣りの2つの頂点
には対角線をむすべないよね。
むすぶと「辺」になっちゃう。
あと、自分には対角線ひけないよね??
対角線をひくためには、
2つの頂点が必要だからね。
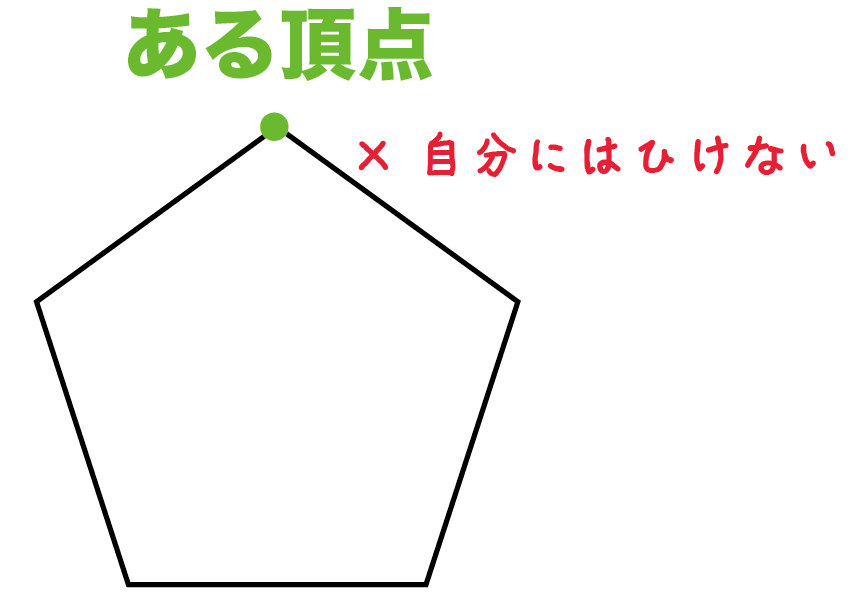
だから、
1つの頂点あたりn-3本の対角線
がひけることになるんだ。
だって、n個ある頂点のうち、
の3つにはひけないからね。
これが公式の「n-3」の意味だよ。
1つの頂点あたり、
「n-3」本の対角線がひける
ってわかったね??
それじゃあn角形ならどうなるかな??
n個の頂点があるから、
n(n-3)の対角線がひけそうだ。
だから、公式で(n-3)にnをかけているんだ。
最後はかぶりをはぶこう。
n角形のとき、
n(n-3)
の本数の対角線がひけそうってわかったね。
だけれども、
この本数にはかぶりがあるんだ。
なぜなら、
1つの対角線を2つの頂点でカウントしてるからね。
たとえば、五角形の対角線を考えてみよう。
下の緑の対角線をイメージしてほしい。
この対角線って、左の頂点1のときも数えているし、
右の頂点2のときもカウントしちゃっているんだ。
1本の対角線を2回ずつ数えていることになる。
だから最後に、
n(n-3)を2でわらなきゃいけないんだ。
どう??
納得いったかな??
多角形の対角線の本数??
そんなの簡単。
n(n-3)÷2
で計算してやろう。
公式をおぼえるのも大事だけど、
なぜ使えるのか??
までおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。七味は必須だね。
中2数学では、
平行線と面積
という単元を勉強していくよ。
はじめて「平行線と面積」ってきいても、
えっ、平行線と?
めんせき?
ってなる。
正直よくわからないはずだ。
そこで今日は、
「平行線と面積」で覚えておきたい2つのこと
をかいてみたよ。
予習や復習につかってみてね。
平行線と面積とはなんだろう??
じつは、これはただの略語なんだ。
なんの略語なのかというと、
「平行線」と「底辺が共通な三角形たちの面積」の性質
だね。
つまり、
「平行線と四角形の面積」のことでもないし、
平行線とただの三角形の面積でもない。
平行線と、底辺が共通な三角形の面積
について勉強していくんだ。
平行線と、底辺が共通な三角形の面積
で覚えたい2つのことを紹介していくよ。
底辺が共通な三角形では、つぎのことがいえるよ。
平行線にはさまれた三角形同士の面積が等しい
ってね。
たとえば、底辺が共通の△ABCと△DACがあったとしよう。
こいつらが、もし、もしも。
平行線ADとBCにはさまれていたら・・・
△ABC と△ABDの面積は等しくなるんだ。
記号であらわすと、
△ABC =△ABD
になるよ。
たとえば、△ABCの面積が16 [cm^2]で、AB//BCだとしよう。
このとき、2つの△ABC と△ABDは底辺がBCで共通だから、
△ABC = △ABD = 16 [cm^2]
になるってわけ!
すごいよね!
つぎはさっきの逆だ。
もし、面積が等しい三角形があって、
しかも、
底辺が共通だったとしよう。
このとき、
底辺じゃない頂点をむすんだ直線と、
底辺は平行になっているんだ。
たとえば、
△ABCと△BCDの面積が等しいとしよう。
このとき、
底辺以外の頂点をむすんだ線分ADは、
底辺BCと平行になっているんだ。
つまり、
AD // BC
ってことさ。
なんとなく便利そうだねw
でもさ、
なんで平行線と面積の性質がつかえちゃうんだろう??
不思議すぎるよね。
じつは、
平行線にはさまれた三角形同士は高さが同じだから
なんだ。
平行な直線って、どーんなに伸ばしまくっても、ぶつからない直線のことだったよね?
ってことは、
平行な直線同士の距離は変わらないってわけさ。
だから、底辺以外の頂点が平行線上にあるとき、
底辺が共通な三角形同士の面積は等しくなるんだ。
だって、
底辺×高さ÷2
のうちの、「底辺」と「高さ」が等しいんだからね。
「平行線と面積」は、
「平行線」と「底辺が共通な三角形たちの面積」の性質
のこと。
これさえおぼえておけば大丈夫。
図形だけじゃなくて、関数の問題でもたまにでてくるから、
しっかり復習しておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。もみじまんじゅうは生にかぎるね。
「平行線と面積」の作図問題ってむずいよね。
たとえばつぎのようなヤツ↓↓
このタイプの問題はテストにもよくでてくる。
だから今日は、
平行線と面積の作図問題の解き方を4ステップでおさらいしていこう。
みためはむずそうだけど、
基本おさえればこっちのものさ。
「平行線と面積」の作図は4ステップでとけちゃうぜ。
用意するものは、
三角定規だけでいいよーー
例題をときながら、作図をマスターしていこう!
まず四角形の底辺を延長してあげよう。
例題でいうと、辺BCだね。
三角定規をつかって右側に延長してやろう。
これが第1ステップ!
四角形の対角線をむすぼう!
四角形ABCDでいうと、
をむすんでやるんだ。
対角線に平行な直線をかいてみよう。
対角線に平行で、
かつ、
四角形の頂点を通る直線だよ。
四角形ABCDでいうと、
対角線ACに平行で、頂点Dを通る直線だ。
三角定規で平行な直線をかいてみてね。
底辺の延長線との交点をEとおこう。
いよいよ最後のステップ。
四角形の底辺と、平行線との交点があるよね。
四角形ABCDでいうとEだね。
こいつと、向かい側にある頂点Aをむすんでやればいいんだ。
すると、
△ABEの面積 = 四角形ABCD
になるよ。
なぜなら、
△ACDと、
△ACEの面積が等しいからね。
この2つの三角形みたいに、
底辺が共通で、高さが等しい三角形の面積は等しいんだ。
いつでも作図できるように練習しておこう!
平行線と面積の作図はどうだった!?
三角定規で平行線をかくだけだから、
なんだかいけそうなきがするね。
あとは問題になれてみて!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ガムはかむほどうまいね。
「正方形」と「扇形」の面積をつかった問題。
たまーにでてくるよね。
たとえば、つぎのような問題だ。
例題
つぎの図形における緑の斜線部の面積を求めなさい。ただし、四角形ABCDは正方形で1辺の長さを8cmとする。
えっ。なんか虫みたい!?
えっ、キモ・・・・
って避けたくなる気持ちもわかる。難しそうだし。。
だけど、解き方をしっていれば、つぎの3ステップで計算できちゃうんだ。
例題をといてみよう。
例題
つぎの図形における緑の斜線部の面積を求めなさい。ただし、四角形ABCDは正方形で1辺の長さを8cmとする。
まず、扇形の面積を計算していくよ。
えっ。
扇形なんてどこにもないって!??
たしかにね。
だけど、よーくみてみて。
じつはこの図形のなかには、
の2つの扇形がかくれているんだ。
それぞれ同じ面積になっているね。
計算してやると、
扇形ABD = 扇形BCD
=半径×半径×中心角÷360
= 8 × 8 × 90°÷360
= 16 [cm²]
になる!
つぎは、正方形の面積を計算していくよ。
例題でいうと、正方形ABCDだね。
(正方形の辺の長さ)×(正方形の辺の長さ)
だったね?
ってことは、正方形ABCDの面積は、
8× 8
= 64[cm²]
になるんだ!
いよいよ最後の仕上げ。
「扇形の面積」をたして「正方形の面積」をひいてみよう。
例題でいうと、
をたして、正方形ABCDの面積をひけばいいんだ。
だから、
(扇形ABD)+(扇形BCD)-(正方形の面積)
= 16π + 16π – 64
= 32π – 64 [cm²]
になるね。
どう??計算できたかな??
「扇形の面積」をたして、
「正方形の面積」をひけばいいんだ。
いろいろな問題にチャレンジしてみてね。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。牛乳ははやめに飲もう。
正方形の面積の求め方には2つあるよ。
それは、
だ。
正方形の辺の長さをつかうか?
それとも、
対角線の長さをつかうか?
で公式がわかれているんだ。
今日はどっちにも対応できるようにするため、
正方形の面積の2つの公式をわかりやすく解説していくよ。
よかったら参考にしてみて。
~もくじ~
まずは、
正方形の「1辺の長さ」をつかった公式だ。
正方形の1辺をaとすると、
つぎの公式で面積が計算できちゃうよ。
aの二乗
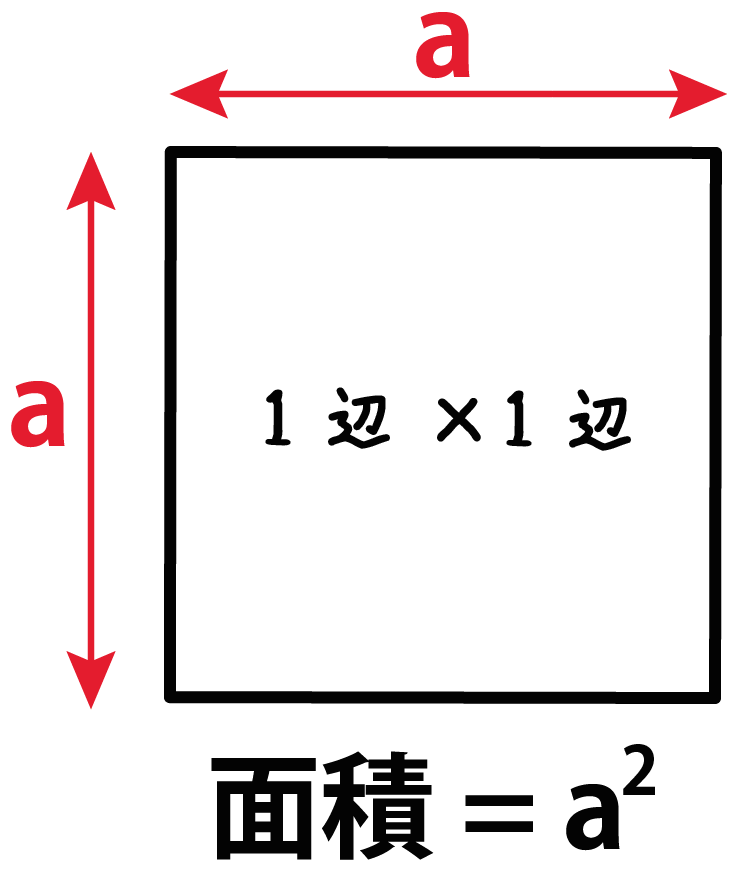
つまり、
(正方形の面積)= (正方形の1辺)×(正方形の1辺)
なんだ。
正方形の1辺がわかってる問題でよく使う公式だよ。
たとえば、つぎのような問題だね。
例題1. 1辺の長さが4cm の正方形の面積はいくつ?
この正方形の1辺は「4 cm」。
よって、この正方形の面積は、
(正方形の1辺)×(正方形の1辺)
= 4 × 4
= 16 [cm^2]
になるね!
正方形の辺を2回かけるだけだから、
簡単でしょ!?
つぎは「対角線の長さ」をつかった公式だよ。
正方形の対角線の長さをaとすると、面積は、
a^2/2
になるね!
つまり、
(正方形の対角線)×(正方形の対角線)÷2
ってことだ。
この正方形の公式は、
対角線の長さしかわからない問題でつかえるよ。
たとえば、つぎのような問題だね。
例題2. 対角線の長さが 10cmの正方形ABCDの面積を求めてください。
この面積の求め方はとっても簡単。
対角線を2回かけて、最後に2でわってやればいいんだ。
すると、
(正方形ABCD) = (対角線AC)×(対角線BD)÷2
= 10×10÷2
= 50 [cm^2]
になるよ。
計算ミスしないように、ゆっくり解いてみてね!
正方形の面積の求め方は2つ。
正方形の、
のどっちかわかれば、面積が計算できるってわけ。
公式で面積をじゃんじゃん計算してやろう。
そんじゃねー!
Ken
こんにちは!この記事をかいているKenだよ。みそ汁はやっぱうまいね。
正方形の面積の公式って、
1辺×1辺
だったよね?
だけど、対角線の長さをつかった公式もあるんだ。
対角線の長さをaとすると、
正方形の面積は、
a^2/2
で計算できちゃうよ。
つまり、
(対角線の二乗)÷2
ってわけだね。
たとえば、
対角線BDが10cmの正方形ABCDがあるとしよう。
この正方形の面積の求め方は、
(対角線)×(対角線)÷2
= 10×10÷2
= 50[cm^2]
になるんだ。
どう??
公式便利でしょ!??
でもさ、
なんで「対角線だけ」で計算できちゃうんだろう??
ちょっと怪しいよね??
じつは、つぎの2つの理由でがあるんだ。
まず、
正方形の対角線の長さが等しいからだね。
正方形の対角線の1本が10 cmだとすると、
もう1本の対角線も10 cmってわけだ。
これは、正方形が長方形の仲間だからいえる。
長方形の性質の、
対角線の長さが等しい
を使えちゃうんだ。
正方形は長方形でもあると同時に、
ひし形でもあるんだ。
だから、
ひし形の面積の求め方である、
対角線×対角線÷2
が使えちゃうんだ。
ひし形は対角線の長さが等しくないよね??
だから、
(ひし形の面積)=(対角線1)×(対角線2)÷2
っていう計算式になるよ。
でも、正方形は対角線の長さが2本とも等しい。
だから、
(正方形の面積)=(対角線の二乗)÷2
という公式になるんだ。
正方形の面積は対角線で計算できる。
あとは、
公式がなぜ使えるのか??
ってとこまでおさえておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。卵は便利だね。
正方形の対角線の求め方には公式があるよ。
正方形の1辺をaとすると、対角線は、
√2 a
で計算できちゃうんだ。
つまり、
(正方形の対角線)= √2 × (正方形の1辺)
ってわけだ。
たとえば、1辺が4cmの正方形ABCDがあったとしよう。
こいつの対角線BDの長さは、
√2 × (正方形の1辺)
= 4√2 [cm]
になるんだ。
正方形の1辺に「√2 」をかけるだけ!簡単だね。
でもさ、
なんで公式がつかえるんだろう??
便利すぎてこわいね。
そこで今日は、
正方形の対角線の長さの求め方を3ステップで解説していくよ。
よかったら参考にしてみてね。
例として、
正方形ABCDの対角線を求めていこう!
正方形に対角線をひいてみよう。
正方形ABCDでいうと、
対角線BDをすーーーーーっとひいてみて。
これが第1ステップだ。
つぎは、正方形の中から直角三角形をみつけよう。
虫眼鏡もルーペもいらない。
裸眼でも大丈夫。
正方形に対角線をひいたら、
直角三角形が2つできあがっているはずだ。
正方形ABCDでいうと、
の2つだね。
直角三角形がみつかれば第2ステップ終了さ。
あとは、三平方の定理をつかうだけ!
直角三角形の斜辺を計算するんだ。
正方形ABCDでいうと、
直角三角形ABDをえらんでみたよ。
この直角三角形で三平方の定理をつかって、
斜辺BDを計算しよう。
BD = √(AD^2 + AB ^2 )
= √(4^2 + 4^2)
= 4√2 [cm]
になるね!
おめでとう!
これで正方形の対角線の求め方をマスターしたね!
正方形の対角線の公式は、
「正方形の1辺」に「√2」をかけるだけ。
むちゃシンプルだね。
だからこそ、なぜ公式がつかえるのか??
を知っておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。髪は軽いほうがいいね。
正方形の定義っておぼえてる??
教科書によると正方形の定義とは、
4つの辺がすべて等しく、4つの角がすべて等しい四角形
ってかいてあるね。
つまり、
ぜーんぶの「辺」と「角」が等しい四角形
ってことなんだ。
だから、
正方形の1つの角度は90°になる。
だって、四角形の内角の和は360°だからね。
んで、1つの辺が4cmだとすると、
ぜーんぶの辺の長さも4cmってことになる。
わかりやすい四角形だね!
ただ、
4つの「辺だけ」がすべて等しくても正方形じゃない。
そいつは「ひし形」だよ。
また、4つの「角だけ」すべて等しくたってダメだ。
そいつは長方形になっちゃう。
4つの「角」と「辺」がすべて等しくなっている四角形が
正方形だってことをおぼえておこう。
最後にひとつだけおぼえておこう。
それは、
正方形が「平行四辺形」でもあり「ひし形」でもあり、「長方形」である
ということだ。
えっ。ぜんぜんよくわからないだって??!
そうだね、順番に説明していこう。
じつは、
正方形は平行四辺形の1種なんだ。
なぜなら、
正方形の定義が平行四辺形になる条件をみたしているからね。
4つの辺・角がすべて等しい四角形
が正方形だったよね??
ってことは、
向かい合う2の辺が等しい、
向かい合う角が等しい
ともいえるね?
だから、
正方形は平行四辺形でもあるんだ。
正方形はひし形でもあるよ。
その理由は、
ひし形の定義をみたしているからなんだ。
ひし形の定義は、
4つの辺がすべて等しい四角形
だったよね??
正方形の辺もすべて等しいから、
ひし形の定義をみたしていることになる。
よって、
正方形はひし形であるわけさ。
長方形の定義をみたしているから
正方形が長方形である
といえるんだ。
長方形の定義は、
4つの角がすべて等しい四角形
だったよね??
ってことは、正方形の定義はそれをみたしているんだ。
だから、正方形は長方形といえるわけさ。
正方形は平行四辺形でもあり、
長方形でもあり、
ひし形でもある、
といってきたね。
長方形・ひし形も平行四辺形だから、
この状態を図にあらわすとこうなる↓↓
つまり、
正方形は平行四辺形でありつつ、
「長方形」と「ひし形」の特徴も同時にあわせもつ、
ハイブリッドな四角形ってことさ。
ぶっちゃけ、
正方形は「CCレモン」と立ち位置がにているね。
清涼飲料水というグループの中に、
のいずれも入ってるはずだ。
CCレモンは、
サイダー(炭酸)とレモン水(レモンっぽさ)の特徴をもっているよね??
清涼飲料水でありつつ、
2種類の飲み物のいいところどりしてるってわけさ。
この立ち位置は正方形とにている。
だって、
正方形は平行四辺形でありつつ、
ひし形と長方形の性質もあわせもっているんだからね。
正方形はCCレモンと似ている
ってことをおぼえておこう!
正方形の定義は、
4つの辺がすべて等しく、4つの角がすべて四角形
だったね。
この定義は「ひし形」と「長方形」の定義もふくんでいる
ってことをおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。替え玉は必須だね。
長方形の性質の中に、
対角線の長さが等しい
ってやつがあるよ。
たとえば、長方形ABCDがあったとしよう。
このとき、
対角線AC = 対角線BD
になるってわけ。
対角線ACが12cmだとすると、
対角線BDも12cmになるんだ。
どう??
むちゃくちゃ便利だよね??
でもさ、
なんで長方形の対角線の長さが等しいんだろう??
不思議すぎるよね。
むしろ、怪しい。
そこで今日は、
なぜ長方形の対角線の長さが等しくなるのか??
を4ステップで解説していくよ。
さっきの長方形ABCDをつかって証明していこう!
証明の方向性としては、
△ABCと△DCBの合同
を証明していくよ。
長方形の定義は、
4つの角がすべて等しい四角形
だったよね??
ってことは、
角ABC = 角DCB = 90°・・・(1)
だ。
長方形は平行四辺形の1種だったね??
ってことは、
平行四辺形の性質がつかえるってわけ。
よって、
2組のむかいあう辺がそれぞれ等しい
より、
AB = DC ・・・(2)
になるね。
BCは共通だから、
BC = CB ・・・(3)
(1), (2), (3)より、
2辺とその間の角がそれぞれ等しいから、
△ABC ≡ △DCB
になるね!
合同な図形の性質をつかってあげよう。
対応する辺の長さはそれぞれ等しいから、
AC = DB
になるね。
ACとDBは長方形ABCDの対角線だね??
だから、
長方形の対角線同士が等しいっていえるんだ!
長方形の性質の、
対角線の長さはそれぞれ等しい
はおさえておこう!
三角形の合同で簡単に証明できるから安心だね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ドタキャンはきついぜ。
ひし形(菱形)の面積の求め方の公式は、
大きく分けて、
2つ
あるんだ。
対角線×対角線÷2
ってやつ。
それと、
底辺×高さ
って公式だ。
どっちも便利だけど、
どっちの公式を使えば良いのか??
迷っちゃうよね。
そこで今日は、
ひし形の面積の求め方を2つわかりやすく解説してみたよ。
よかったら参考にしてみてー
〜もくじ〜
対角線で「ひし形の面積」を計算できちゃう公式だ。
さっきも紹介したけど、
対角線×対角線÷2
で計算できちゃうんだ。
つぎの「ひし形ABCD」の面積を求めてみよう。
対角線AC・BDの長さがわかっているね??
だから、
対角線の公式をつかうと、
(対角線)×(対角線)÷2
= 10×12÷2
= 60 [cm^2]
になるね。
でもさ、
なんで菱形の面積を公式で計算できるんだろう・・・
って思うよね。
じつは、
ひし形の4つの頂点を通る、
長方形の半分の面積になっているからなんだ。
ひし形ABCDの周りに長方形EFGHをかいたとしよう。
はそれぞれ合同になっているね。
ってことは、
△ADMを△ABMの位置に、
△DMCを△CFBの位置に移動させてもいいわけだ。
つまり、
菱形ABCDは長方形AEFCと等しくなるってわけ。
「長方形AEFCの面積」は長方形EFGHの半分になっているね??
よって、
(ひし形ABCDの面積 )=(長方形EFCA)
= (長方形EFGH)÷2
= (対角線)×(対角線)÷2
になるんだ。
つぎは、「底辺」と「高さ」をつかった公式だよ。
菱形の面積は、
(底辺)×(高さ)
で計算できちゃうんだ。
たとえば、つぎのような菱形ABCDだね。
のひし形だとすると、こいつの面積は、
10×12
= 120[cm^2]
と計算できちゃうんだ。
なぜ、
底辺×高さ
っていう公式がつかえるんだろう??
じつはこれは、
ひし形が平行四辺形であるからなんだ。
※詳しくはひし形の定義をみてね。
平行四辺形の面積は「底辺×高さ」で求められたよね??
菱形は平行四辺形ともいえるから、
この面積の公式も使えちゃうってわけさ。
じゃんじゃん計算していこう!!
ひし形の面積の求め方は、
の2通りがあるよ。
問題によって使いわけていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。明太子が恋しいぜ。
ひし形の対角線にはつぎの性質がある。
それは、
対角線は垂直に交わる
ってやつだ。
たとえば、ひし形ABCDがあったとしよう。
対角線の交点をMとすると、
AC⊥BD
になるんだ。
つまり、
角AMD = 90°になるってわけ。
むちゃ便利そうな性質だね。
だけど、
なぜ、ひし形の対角線は垂直に交わるんだろう??
ちょっと不思議すぎるよね。
そこで今日は、この謎を証明していくよ。
よかったら参考にしてみて。
さっそく証明していこう。
つぎの4ステップで証明できちゃうんだ。
例の「ひし形ABCD」をつかって証明していこう。
証明の方向性としては、
△ABMと△ADMの合同を証明していくよ。
△ABMと△ADMにおいて、
ひし形の定義(4つの辺がすべて等しい)より、
AB = AD・・・(1)
ひし形は平行四辺形だから、
平行四辺形の性質がつかえるね。
対角線は中点でそれぞれ交わる
という性質より、
BM = DM・・・(2)
AMは共通だから、
AM = AM・・・(3)
(1)・(2)・(3)より、
3つの辺がそれぞれ等しいから、
△ABM ≡ △ADM
がいえるね。
合同な図形同士の対応する角はそれぞれ等しいから、
角AMB = 角AMD・・・(4)
になるね。
角AMBと角AMDをたしたら直線になっているから、
角AMB + 角AMD = 180°・・・(5)
になるはず。
(4)、(5)より、
角AMD + 角AMD = 180°
角AMD = 90°
になるね。
よって、
ひし形ABCDの対角線は垂直に交わることになるよ。
ひし形の性質でおさえておきたいのは、
対角線が垂直に交わる
ということ。
性質をただ暗記するだけじゃなくて、
なぜ対角線が垂直に交わるのか??
ということもおさえておこう。
そんじゃねー
Ken