こんにちは!この記事をかいているKenだよ。塩は大事だね。
ってことは習ったね。
だけどさ、
実際、素因数分解ってどうやるんだろう??
やり方なんてぜんぜんイメージできないよね。
だって、素因数分解したことないんだもん。
そこで今日は、
素因数分解のやり方を5ステップで解説してみたよ。
よかったら参考にしてみて。
素因数分解のやり方はずばり、
素数でわりまくって、割れた素数を集めて因数にする
方法だ。
だから、素因数分解で大切なのは、
素数で割りまくる根性
と、
素数かどうか見分ける力
なんだ。
この2つさえあれば素因数分解なんて楽勝さ。
素因数分解は5ステップでできちゃうよ。
例として、自然数の360を素因数分解してみよう!
まず、素因数分解したい自然数をかいてみよう。
鉛筆でもシャープペンでもいいからかいてみて。
例題でいうと、
360
だね。
うまくかけたらつぎにいこう。
つぎは素因数分解するための準備。
自然数の周りに線をかいてみて。
これは素数で割りまくるための道具なんだ。
この線の横に、自然数を割る素数、
自然数の下にその割り算の答えをかいていくんだ。
もし、「割り算の答え」が素数でわれるようだったら、
こんな感じで下に続けていって、素数でわりまくるんだ。
例題でもおんなじさ。
360の下にこのきんとんうんのような線をちょこっとかいてあげよう。
これが第2ステップ!!
いよいよ素因数分解の山場。
素数でわりまくる
っていうステップだ。
ここでのコツは、
小さい素数から割りまくる
ってこと。
つまり、素数でいちばん小さい「2」から割りまくるのさ。
2で割り切れなくなったら3、
3で割り切れなくなったら5、
・・・・
というように徐々に素数を大きくしていこう。
割り算の答えが1になるまで続けてみてね。
例題の「360」もまずは素数2でわりまくってみよう。
すると、
っていう感じで3回われたね!
45は残念ながら2で割り切れないから3にバトンタッチだ。
おなじように、3で割りまくってみると、
っていう感じで2回われたね。
お次は素数の5の出番。
おなじように割り算の答えをわってみると、
・・・
おや!
1がでてきたね!
割り算の答えが1になったからストップ。
割ってきた素数を集めるフェーズだ。
左の素数をかきあつめて「×」でむすんでみよう。
たとえば、自然数が素数1から素数nまでわれちゃったとしよう。
このとき、割れちゃった素数を「×」でむすんでやると、
素数1×素数2×素数3×・・・×素数n
になるね。
これを360の素因数分解でもやってみよう。
割った素数はぜんぶで、
の6つだね??
こいつらを「×」でむすんでやると、
360 = 2×2×2×3×3×5
になるね。
最後は指数でシンプルにしよう。
同じ素数を指数でまとめればいいのさ。
360の素因数分解でいうと、
が指数でまとめられそうだね。
指数でコンパクトにしてやると、
360 = 2^3 × 3^2 × 5
になるはずだ。
おめでとう!
これで素因数分解のやり方もマスターだね。
素因数分解は基本的に、
素数で自然数をわりまくって、
あつめて、
かけ算にしてやるだけ。
あとは指数でととのえればよし。
素因数分解はいろいろな計算に使えて便利。
やり方・解き方はおぼえておこうね。
えっ、もっと高速に素因数分解したい??
そんな君のために、素因数分解電卓アプリ「Soin」をつくったよ。
よかったら試してみて。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。強風にあおられたね。
世界にはたくさん因数分解がある。
地球は広い。ほんとに。
その因数分解の1つに、
素因数分解(そいんすうぶんかい)
ってものがある。

名前からしてちょっと怪しい。
ぶっちゃけ遠ざけたい。
だけど、テストにでてくるくせ者なんだ。
そこで今日はこの「素因数分解」と仲良くするためにも、
素因数分解とはなにか??
を解説してみたよ。
よかったら参考にしてみて。
ずばりいってしまおう。
素因数分解とは、
「自然数」を「素数」の「かけ算」になおすこと
だよ。
もっと因数分解的にいってやると、
自然数を素数の因数に分解すること
なんだ。
素数の因数のことを略して「素因数」ってよんでるよ。

えっ。
ごちゃごちゃしてるって!??
うーん、そうだね。
たとえば、35という自然数をイメージしてみて。
こいつを素因数分解、つまり、
素数のかけ算になおしてやると、
35 = 5 × 7
になる。
だって、「しちごさんじゅうご」だもん。
「5」も「7」も素数だから素因数分解になるんだ。
このとき、
「5」と「7」を「35」の「素因数」ってよんでるよ。
なぜなら、素数の因数だからね。
せっかくだから、
素因数分解じゃない例を紹介していくよ。
どれか1つにあてはまるようなら、
そいつはもう、素因数分解でもなんでもない。
ただの因数分解ってことさ。
因数分解する数字が「自然数」じゃない
っていうケースだ。
スタート地点から間違っているね。
たとえば、
-35
を「- 5 × 7」に因数分解したとしよう。
いっけん素因数分解っぽいけど、こいつは素因数分解じゃない。
なぜなら、
因数分解したもとの「-35」が自然数じゃないからね。
素因数分解かたしかめるときは、かならず、
もとの数が自然数かどうか
をチェックしてみよう。
つぎは、因数が素数じゃないケースだ。
これはヒューマンエラーというか、ただのミスだね。
たとえば、もし、35を「1×35」って因数分解しちゃっとしよう。
この因数分解は素因数分解なんかじゃない。
なぜなら、
は素数じゃないからね。
因数分解はできてるんだけど、素数のかけ算に分解できてないんだ。
だから、ただの因数分解になっちゃってる。
素因数分解したあとにはかならず、
因数が「素数」になっているかどうか
を確認してみよう!
素因数分解とは因数分解の一種。
自然数を素数の因数に分解することを「素因数分解」っていうんだ。
テストによくでてくるから、
素因数分解のやり方もおさえておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鮭は焼くとうまいね。
数学の先生から、
1から100までの素数を覚えなさい
って言われた??
えっ。
ふつうにむちゃむちゃ。
だって、1から100までの素数は「25」個もあんだぜ??
いくらなんでも無理な注文だよ。
しかも数字なんて覚えにくい。
電話番号でギリギリ。
1から100までの素数なんて覚えられねえ。。。
まじ助けて欲しい・・・・・
・・・・・・・・・・・・・
そんなときに役に立つのが「語呂合わせ」というアイテム。
25個の素数をたのしみながら覚えられるんだ。
今日はマイ勉オリジナルの、
1から100までの素数の覚え方がわかる語呂合わせ
を紹介するよ。
よかったら参考にしてみて。
語呂がストーリーになってるよ。
読みながら「1から100までの素数」がおぼえらるはず。
さっそくよんでみよう!
兄さんと午後にセブンイレブンにいってみた。。
2, 3 5, 7, 11
意味もなく、ブラブラしてみたけど、誰もいないじゃん。
13, 17
暇すぎるから、塾で勉強しようかと思ったぐらいだよ。
19
そしたらさ!
兄さんがおれの肉まん食べちゃったんだよ。
23, 29
もうケンカだよ、ケンカ。
しかも、
肉まんだけじゃない。
サーティーワンアイスまでみな食べちゃったんだよ。
31, 37

もう、信じられる???
よい子のふりして立ち読みしてる場合じゃなかった!
41, 43
しかも兄さん、
しなっとしたゴミ袋おれにわたしてさ、
47, 53
「ご苦労さん」
59
っていったんだ。
ふざけんな!
おれに肉まんとアイス買ってよ!!泣
無意味にむなしいだけじゃん!
61, 67

財布もってないんだよ。
71
これじゃあ、
牛丼の並み盛りも食えねえよ。
73
もう、
泣くしかないぜ。
79
もうわかった。
いいよ、兄さん。
くれぐれも、
ヤーさん・ヤクザの急な絡みに気をつけてね。
83, 89, 97
・・・・・・・・・・・
と以上が語呂合わせだ。
最後はミステリアスな展開になったね。
ストーリーをおさらいして、
1から100までの素数をおぼえてみよう!
1から100までの素数??
そんなの語呂で一発さ。
25個もあるけど大丈夫。
どうしようもない兄弟ケンカの物語を思い浮かべればいいんだ。
がんばって暗記してみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。腸の調子がいいね。
中3数学では、
素数(そすう)
を勉強していくよ。
いままで、
整数とか、自然数とか、約数とか、公倍数とか、最小公倍数とか・・・・
いろいろな数をならってきたね。
だけど・・・・
素数なんて一度も聞いたことがない!
って驚いてると思うんだ。
だから今日は、
「素数とは何か」をわかりやすく解説してみたよ。
よかったら参考にしてみて。
〜もくじ〜
素数をWikipediaでしらべてみると、
正の約数が 1 と自分自身のみである自然数で、1 でない数のこと
ってかいてあるね。
ちょっとよくわからない!? うん、ちょっとむずい。
もっと簡単にいってやると、
「1」と「自分」でしか割り切れない自然数のこと
だよ。
えっ。
まだピンときてないだって!??
そうだね。
素数の具体例をみていこう!
いきなりだけど、数字の「5」をイメージしてほしい。
そうそう。
よくある数字の5だよ。
じつは「5」は素数なんだ。
なぜなら、
1
と
5(自分)
でしか割り切れないからね。
あっ、自然数の割り算に限定したときね。;
2で割っても余り1になっちゃう。
3で割っても余りが2になっちゃう。
4でも無理ゲーだね。
「5」を割り切れる自然数は、
「1」と「5(自分)」しかない。
うん、ないない。
だから、
「5」は「素数」といえるんだ!
つぎはそのお隣の、
6
をみてみよう。
「6」という自然数は、
素数じゃない
んだ。
なぜなら、
1と自分(6)以外の自然数でも割り切れちゃうからね。
2でも割り切れちゃうし、
3でも割り切れる。

よゆーで、
「1と自分以外の自然数」でわりきれちゃうじゃん。
だから、「6」は素数ではないんだ。
どう??納得したかな??
雰囲気的に、
1は素数なのかも・・・・
って思っちゃうかもしれない。
だって、「1」と「自分(1)」で割り切れちゃってるし。
だけど、覚えておいてほしいのは、
「1」は素数でもなんでもない
ってこと。

これだけはおさえておこう。
なんだろうな、そういうものだと思っちゃおう。
星は夜空に輝くものだとか、
熊はほ乳類だとか、
週刊少年ジャンプは面白いだとか・・・
みたいな感じでそういうものだと思おう。
えっ。
納得しないだって?!
どっからどう見ても1が素数にみれるって??
うーん、そうだな。
こう覚えてみたら??
素数とは、
「1」と「自分」でしか割り切れない自然数で、
「1」と「自分」はいっしょになっちゃいけない
ってね。
こう覚えておけば、1が素数じゃない気がしてくる。
なぜなら、
1にとっての「自分」は「1」だからね。
とにかく。
「1」は素数じゃない
っておぼえておこう!!
素数とは何かをここまで解説してきたね。
どう??納得したかな??
数学を勉強していて、
あれ・・・素数ってなんだろう・・・??
って思ったらちょっとストップ。
基本を復習してみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。チーズとバターは紙一重だね。
中3数学を勉強してると、
因数(いんすう)
ってでてくるね??
小学校の算数じゃきいたことない。
友だちと因数について話すチャンスもない。
うん、むずかしそうだし、よくわからない。。
そこで今日は、中3数学でスタートダッシュをきるためにも、
因数とはなにか??
を解説してみたよ。
よかったら参考にしてみて。
因数とはずばり、
ある数・文字式を、あえてかけ算であらわしたときに、
かけられている数・文字式のこと
だよ。
えっ。ぜんぜん意味がわからないだって?!?
そうだね。
因数の具体例をみていこう!
文字と数にわけて考えてみたよ。
まずは「数」の因数の例だね。
そうだなあ、たとえば、
21
っていう自然数をイメージしてみて。
あえて。
あえて、かけ算の形になおしてみると、
7×3
にできるよね???
だって、「さんしちにじゅういち」だからさ。
ある数をかけ算になおしたとき、
かけられているものを「因数」というんだったね??
ってことは、21の因数は、
だ。
どう??
ちょっと因数に近づけたかな???
つぎは「文字式」の因数の例だね。
例として、
a² – a
をイメージしてみて。
この文字式もあえて、
あえて、かけ算になおしてみるんだ。
aで()でくくってやると、
a × (a – 1)
っていうかけ算になるよね。
かけ算になおしたときに、かけられているやつが「因数」。
よって、a² – aの因数は、
の2つになるんだ。
どう??
文字式の場合もしっくりきた??
因数とはなんだろう??
そう感じたらまず、
数や文字式を「かけ算」になおしてみよう!
そうすれば因数がでてくるはずだ。
がんばって探してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。シロップに要注意だね。
中学数学でならう公式は3つある。
ぶっちゃけ公式覚えてれば大丈夫。
もうね、楽勝。
公式通りに計算すればいいからね。
だけどさ、
乗法公式はなんでつかえるんだろう??
ぶっちゃけ怪しいんだよね。
知らないおじさんについていくみたいでさ。
そんな疑問を解消するために今日は、
乗法公式(式の展開の公式)はなぜつかえるのか??
を解説していくよ。
よかったら参考にしてみてね。
式の展開の公式を証明するために使うのはただ1つ。
それは、
さ。
えっ。分配法則なんて忘れただって??
そうだね。
分配法則とはずばり、
()の外側の数字や文字を()内の項に順番にかけて展開すること
だよ。
たとえば、
(a+b)(c+d)
っていう計算式があったとしよう。
分配法則つかえば一瞬で展開できるんだ。
まず、「a」をうしろにある()内の項にそれぞれかける。
そして、たす。
(a+b)(c+d)
= ac + ad
つぎは「b」をうしろの()内の項にかけて、たしてやるんだ。
つまり、
「b」を「c」と「d」にかけてたせばいいのさ。
よって、
(a+b)(c+d)
= ac + ad +bc + bd
になるね。
この分配法則が使えればOK。
乗法公式も証明できちゃうよ。
さっそく一つ目の、
(x+a)(x+b)
を証明してみよう。
分配法則で展開してやればいい。
まず、「x」をうしろの()の2つの中にかける。
(x+a)(x+b)
= x^2 + bx
つぎは、「a」をうしろの2つの項にかけてたしてやる。
すると、
(x+a)(x+b)
=x^2 + bx +ax +ab
になるね。
あとは同類項「bx」、「ax」をまとめるだけさ。
(x+a)(x+b)
= x^2 + bx +ax +ab
= x^2 +(a+b)x + ab
すると、乗法公式のできあがり!
いっちょ上がりさ。
つぎは平方の公式の証明だね。
こいつも分配法則で証明できちゃう。
まず、(a+b)^2をかけ算になおしてみよう。
すると、
(a+b)^2
= (a+b)(a+b)
になるね。
これをさっきみたいに分配法則で展開してみよう。
まず、いちばん左の「a」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab
つぎは、「b」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
あとは同類項をまとめるだけ。
すると、
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
= a^2 + 2ab + b^2
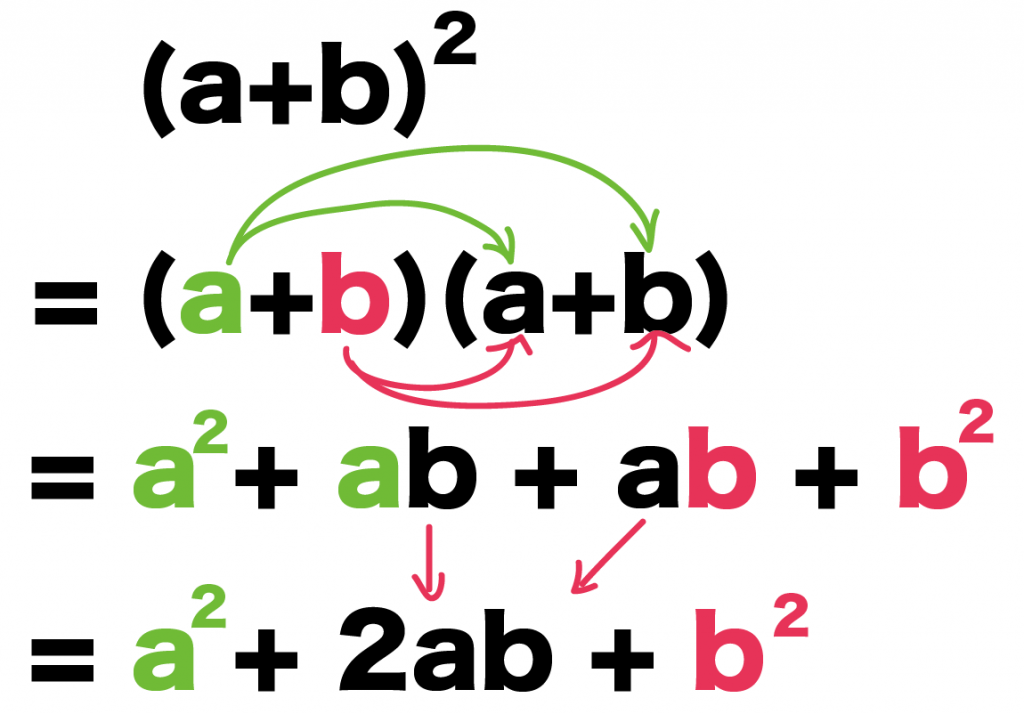
あら。
平方の公式のできあがり!
いよいよ「和と差の積」の公式の証明だ。
こいつも分配法則で一発。
まず、いちばん左のaを右の()内の項にかける。
そして、たす。
(a +b) (a-b)
= a^2 – ab
2つめの「b」を後ろの()にかけてやると、
(a +b) (a-b)
= a^2 – ab +ab -b^2
になるね。
あとは同類項をまとめてやろう。
の2つだね。
こいつらをたして消してやると、
ほら!
乗法の公式の「和と差の積」のできがあがり。
乗法公式を覚えることは大切。
だけど、
テストで忘れたら危機。危機におちいる。
だからこそ、
なぜ乗法公式がつかえるのか??
ってとこまでおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。おしぼりはアツいほうがいいね。
中学3年生で最初にならうのは、
式の展開のやり方
だ。
一度マスターすればもう大丈夫。
どんな展開の問題もとけちゃう。
テスト前に身につけておきたいワザだね。
そこで今日は、
式の展開の問題の解き方
を3ステップで解説していくよ。
よかったら参考にしてみて。
さっそく解き方を紹介していこう。
つぎの3ステップでとけちゃうよ。
いっしょに例題をといていこう。
例題
次の式を展開しなさい。
(x+1)(x+3) -3 (2x +6)
はじめに、
乗法公式がつかえるかどうか
を確認しよう!
公式がつかえる??
じゃあガンガン使おうぜ。
例題をみてみると、
(x+1)(x+3)
で公式がつかえそうだね。
公式で展開してやると、
(x+1)(x+3)
= x^2 + 4x + 3
になるはず。
まず公式つかえるか確認。
いけそうなら公式をつかう。
これが第1ステップさ!
つぎは分配法則で展開してやろう。
()をはずす
ってこと。
ゆっくり計算してみよう。
例題でいうと、後ろの、
-3(2x + 6)
で分配法則がつかえそうだね。
()をはずしてやると、
-3(2x + 6)
= -3×(2x) -3 × 6
= -6x -18
になるね!
これが第2ステップ!!
最後に同類項をまとめてみよう。
同類項って、
文字と次数がおなじ項のこと
だったね。
たとえば、
とか。
文字はおなじで、
かけられている数が同じなら「同類項」というんだ。
例題では、
が同類項だ。
なぜなら、文字と次数が一致しているからね。
数字は数字同士が同類項になるよ。
同類項はまとめることができる。
係数同士をたしてやると、
になるはず。
おめでとう!!これで式の展開が完了したよ。
式の展開の解き方はカンタン。
の3ステップでいいんだ。
乗法公式おぼえるのが大変だけど、
問題をときまくっておぼえていこう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。風呂リフォームしたいね。
中3数学ではじめにならうのは、
式の展開
という単元だね。
うきうき気分で新学期をむかえた。
だけど、
式の展開っていったいなんだろう??
って思わない??
日常生活ではゼッタイに使わない単語だし。
おまえ昨日、式の展開みたー?
なんて言わないよね。
今日は新学期からつまずかないために、
式の展開とはなにか??
を解説していくよ。
よかったら参考にしてみて。
式の展開とはなんだろう??
教科書をみてみると、
積の形で書かれた式を計算して、和の形で表すこと
ってかいてあるね。
もっと簡単にいうと、
「かけ算の式」を計算して「足し算の式」にする
ってことさ。
たとえば、
A×B
っていうかけ算の式があったとしよう。
こいつを計算して、
足し算の形にしてやるんだ。
このことを、
「A×B」を展開する
っていうよ。
えっ。
イマイチわからないだって??
たしかに。
これじゃあピンとこないよね。。
式の展開の具体例をみてみようか。
たとえば、
(2a+5b)(3a-b)
っていう「かけ算の式」を展開してみよう。
これを分配法則で計算してやると、
(2a+5b)(3a-b)
= {2a×3a +2a × (-b) +5b × 3a + 5b×(-b)}
= 6a^2 -2ab +15ab -5b^2
= 6a^2 +13ab -5b^2
になるね。
この計算のことを、
(2a+5b)(3a-b)を展開する
っていうんだ。
どう??ピンときたかな??
式の展開はシンプル。
「かけ算の式」を計算して「たし算の式」にすること
を展開というんだ。
式の展開のやり方をいっしょに勉強していこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。カフェはやっぱいいね。
中学2年生になると、
二元一次方程式
を勉強するよね??
正直、聞いただけでもむずかしそうだし、数学が嫌いになっちゃいそうだ。

いや。
いやいや。
大丈夫。
そんなときはこの記事を読んでみて。
二元一次方程式の意味がしっくりするはずさ。
〜もくじ〜
二元一次方程式って、
2種類の文字が使われている一次方程式のこと
なんだ。
もっと簡単にいうと、
2種類の文字が入っていて、1つの項あたり最大1回文字がかけられている方程式
のことなんだ。
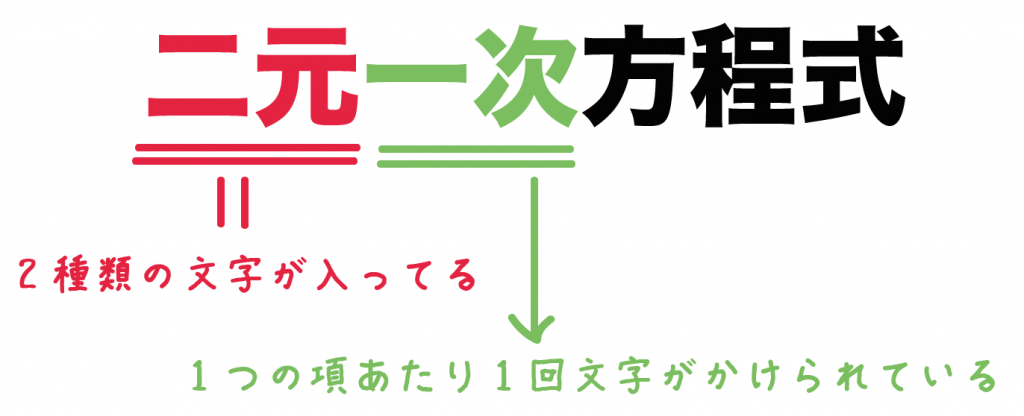
たとえば、
2x – 5y = 26
とかね。

この方程式は、
xとyの「2種類」の文字が使われていて、
なおかつ、
1つの項に1回ずつ以下ずつ文字がかけられているからね。
じつは、
ってことを表しているんだ。
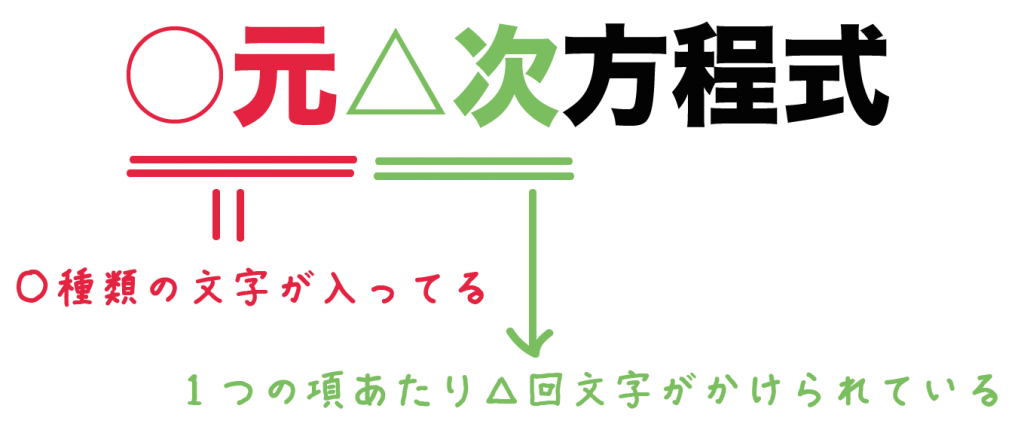
だから、
x + y + z = 90
っていう方程式は「三元一次方程式」だし、

2x + xy + z^4 – w = 90
っていう方程式は「四元四次方程式」になるのさ。

数学の先生に、
この方程式は何元何次方程式ですか??
ってきかれたら、
ということを見極めよう。
即答できればクラスの人気者さ!
二元一次方程式にも「解」があるよ。
方程式の「解」って、
文字に入れても等式が成り立つ「数字」のこと
だったよね。
たとえば、さっきの「2x-5y = 26」という二元一次方程式の解は、
・・・・・・・・・
などなど・・・2つ以上あるよね。
どうしよう・・!
解が1つじゃねえよ・・・・
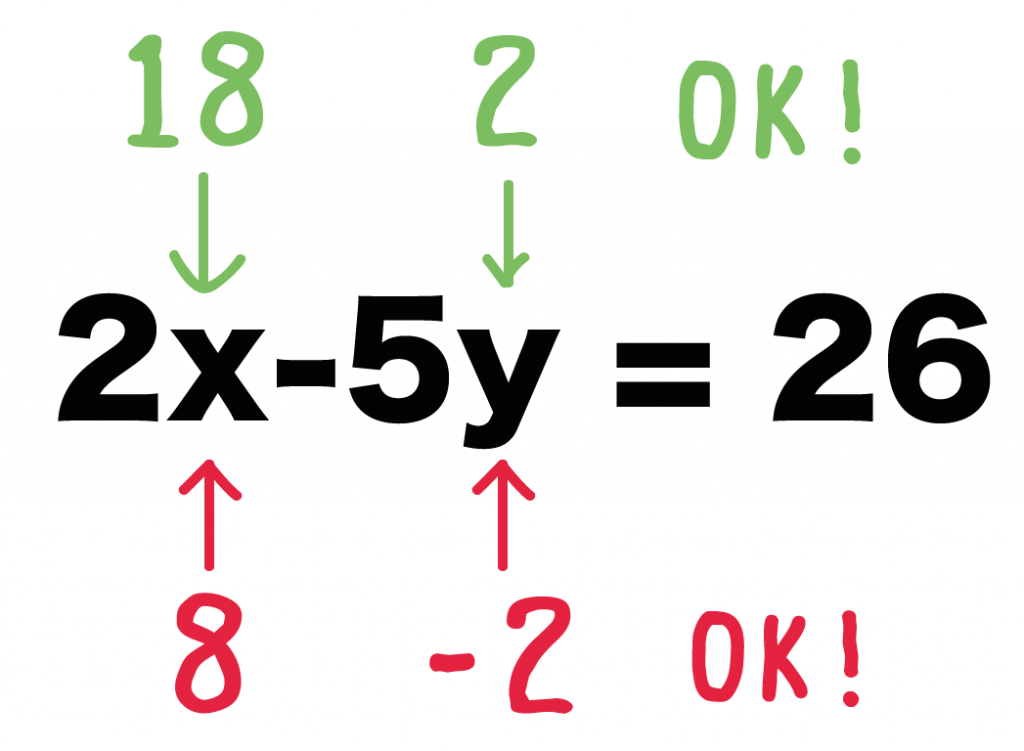
じつは、二元一次方程式1つだけでは解が1つに定まらないんだ。
二元一次方程式の解を求めるには、
2つ以上の二元一次方程式が必要だよ。
たとえば、
っていう2つの方程式があったら、
さっきの2つの解のうち、
しか成り立たなくなるよ。
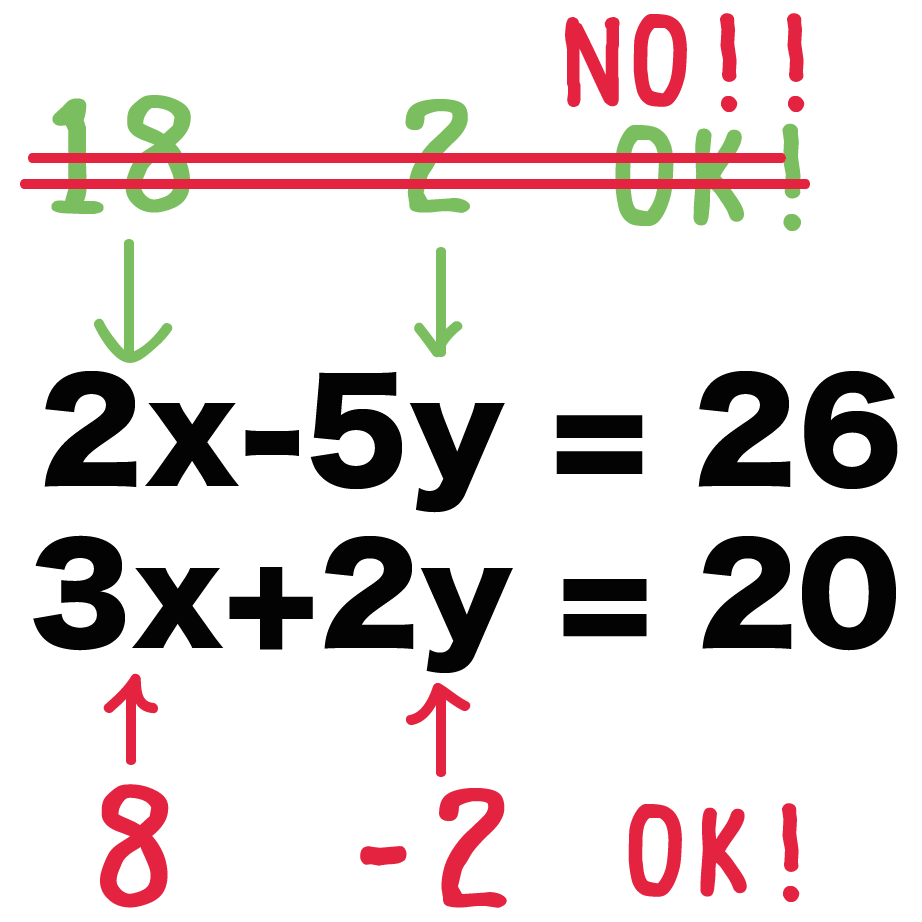
ってことで、
二元一次方程式の解を1つに決めたかったら、
2つの二元一次方程式を用意する
ってことをおぼえておこう。
このように、2つの方程式を組にしたものを「連立方程式」っていうんだ。
これから連立方程式をみっちり勉強していくよー!。
二元一次方程式って呪文みたいに聞こえるけど、
じつはシンプル。
2種類の文字が入った一次方程式のことなんだ。
もっと簡単にいってしまえば、
2種類の文字が入っていて、1つの項あたり最大1回文字がかけらている方程式
のことなんだ。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。家具の匂いが好きだね。
文字式の計算でいちばんむずかしいことって、
分数の通分
だよね。
分数だけでヤッカイなのに、それが文字になる?!?
たまったもんじゃない。

そこで今日は、
分数の文字式の通分方法
を3分で解説するよ。
通分がどうしてもできねえ!ってときに参考にしてみて。
〜もくじ〜
文字式の分数の通分方法を勉強する前に、
分数の通分ってなに??
ということを確認しよう。
これがわかってないと文字式の通分どころじゃないからね。
通分って、
2つ以上の「分母の違う分数」を1つにすること
なんだ。

これが分数の通分っていうものさ。
たとえば、
1/2 + 1/3
っていう分数式を通分して1つにしてやると、
5/6
になるんだ。
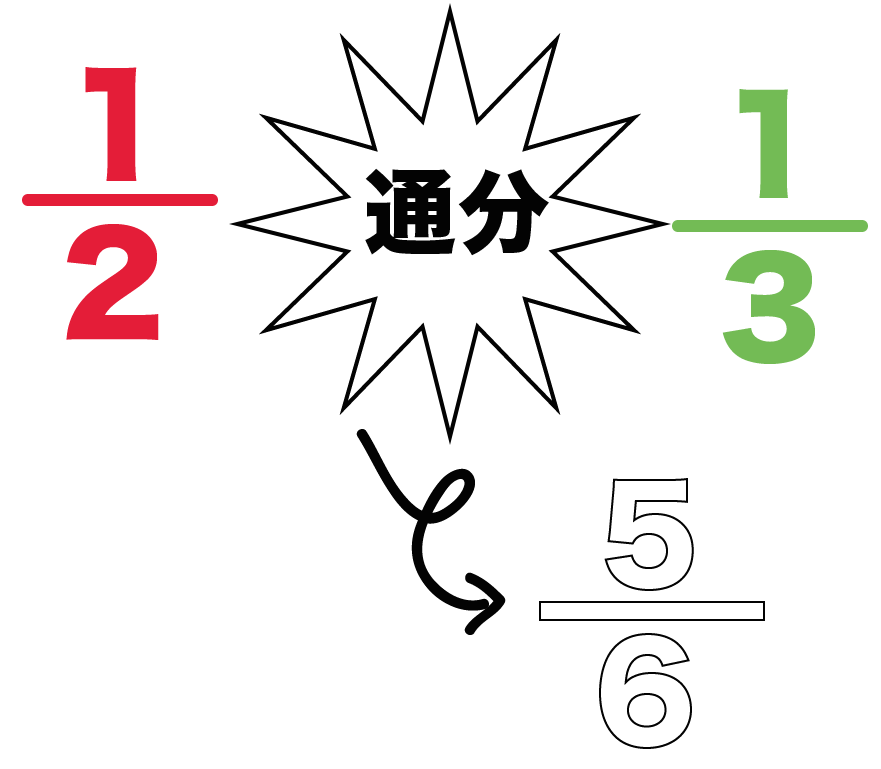
これを文字式の分数でもやっていくってわけさ。
分数の文字式を通分する方法は、
っていう2ステップだ。
分子と分母を順番に計算すればいいってことだね。
つぎの例題をときながら通分をマスターしていこう!
つぎの分数の文字式を通分して1つにしなさい。
2b/a – 5d/c

まずは通分後の分母をきめちゃおう。
通分後の分母は、
分母をかけあわせたもの
なんだ。
例題の計算式の2つの分母は、
だったよね??
こいつらをかけあわせてやればいいんだ。
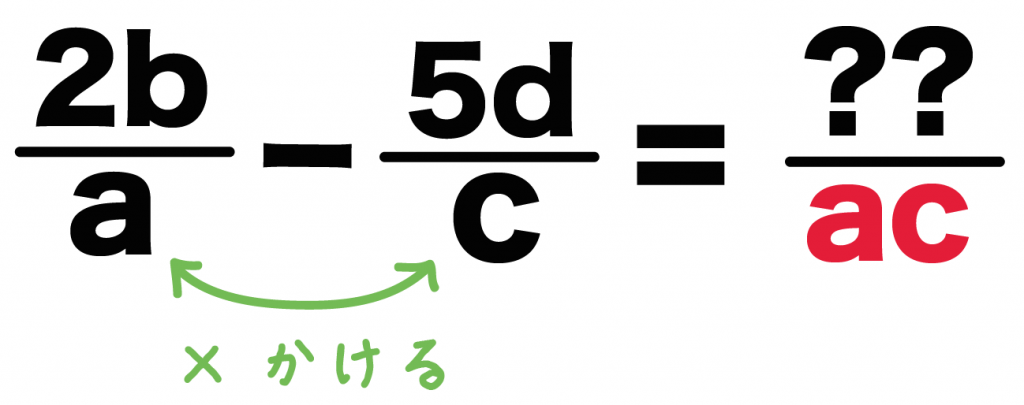
その答えが通分した分母になるってわけ!
あとは分子だ!
通分後の分子の計算方法は、
たすきがけ
というものさ。
「自分の分母」と「相手の分子」をかけたものを足し合わせればいいんだ。
ななめに掛け合わせるようすが「駅伝のたすき」に似てるから、
「たすきがけ」って呼ばれているんだ。
例題でいうと、
っていう計算をして、そいつらを足してやればいいんだ。
足したものが通分後の「分子」になるのさ。
それぞれ計算してやると、
になる。そんで、そいつらをたしあわせてやると、
2cd-5ad
になるよね。こいつが通分後の分子になるわけさ。
ってことで、
最終的に例題の分数を通分すると、
(2bc-5ad)/ac
になるよー!
おめでとう。 これで文字式の分数の通分もマスターできたね!
分数の文字式の通分はどうだったかな??
っていう2ステップで簡単に計算できちゃうはず。
中学数学の基礎だから、ここでマスターしておこうね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。10円玉募金をはじめたね。
分数がふくまれる「等式の変形」ってむずかしいよね。
整数だけでもヤッカイなのに、分数がはいったらもっとヤバい。
そこで今日は、
「分数がふくまれている等式の解き方」をわかりやすく解説していくよ。
分数がふくまれる「等式の変形」には2つのパターンがあるんだ。
まず1つ目は分母を払うパターンだ。
これは「求める文字」が分子にあるタイプだね。
たとえば、
つぎの等式をaについて解きなさい。
a/2 + b/5 = 2
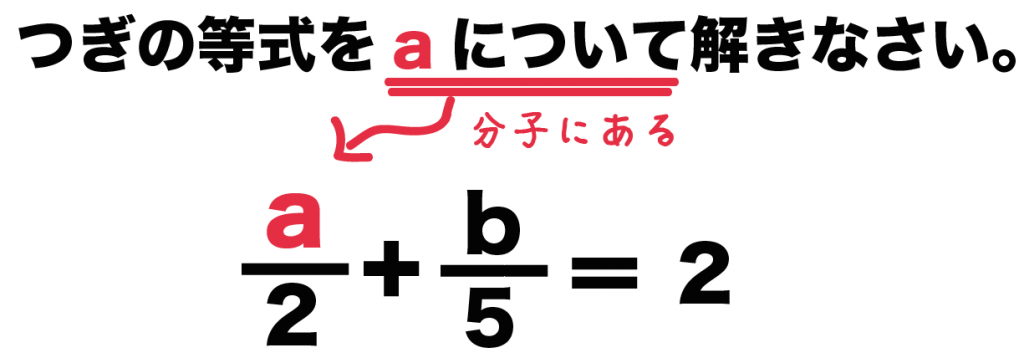
っていう問題だ。
これは、
○○について解きなさい
っていう○○の文字が分子にはいっているよね。
このタイプの問題はつぎの3ステップでとけちゃうんだ。
まず分母をはらっちゃおう。
等式から分数を消せちゃうってわけ。
つまり、
分母の最小公倍数を等式全体にかけてやればいいのさ。
例題でいうと、
分母の「2」と「5」の最小公倍数は「10」だよね。
こいつを等式の両辺にかけてみると、
10×(a/2 + b/5) = 2 × 10
5a + 2b = 20

になるね!
分母をはらった??
そのつぎは移項だね。
「求めたい文字」を左辺に移動させよう!
それ以外は反対の右辺におしこんでね。
例題でいうと、
等式で求める文字は「a」だったよね??
ってことは「a」をふくむ項を左に、ソレ以外の項を右によせてやろう!
すると、
5a + 2b = 20
5a = 20 -2b
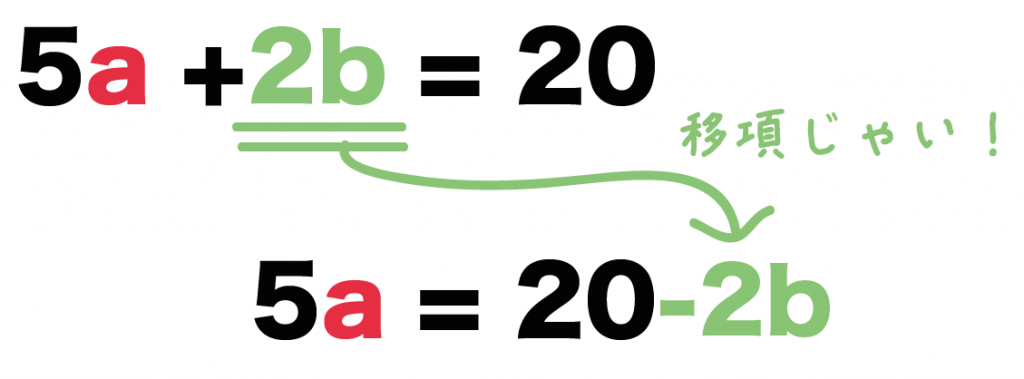
になるね!
移項するときに、項の符号が変わることに注意してね。
最後は「求める文字」の係数をとってあげよう!
求める文字の前についている「数字」が係数だよ。
こいつで両辺をわってあげよう!
すると例題の式は、
5a ÷ 5 = (20-2b) ÷5
a = (20-2b)/5
になるね!
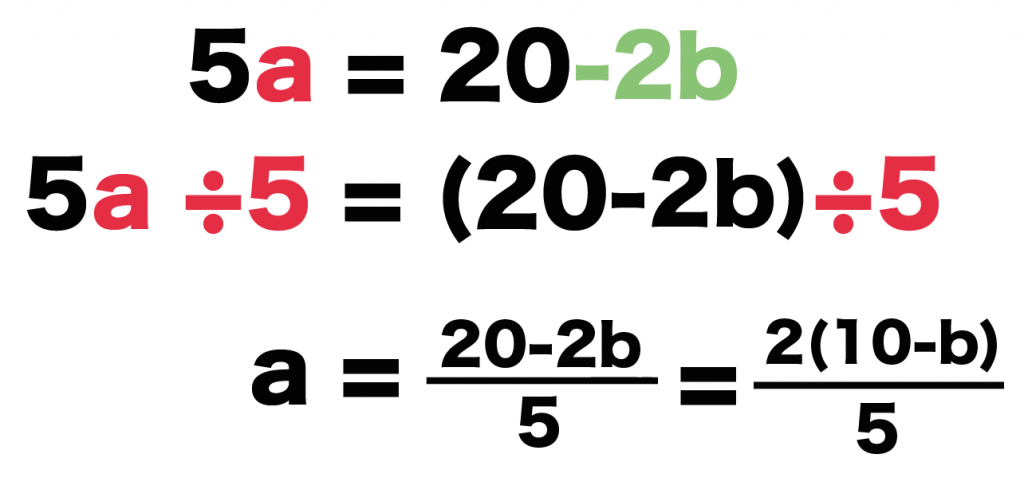
これで分母をはらうやり方はオッケーだね!!
等式の変形の2つ目のパターンは、
「求める文字」が分母にある場合だ。
たとえば次の問題のように、
つぎの等式をaについて解きなさい。
1/a + 1/b = 1/c
「〜について解きなさい」の「〜」が分母にはいっちゃっているパターンだ。
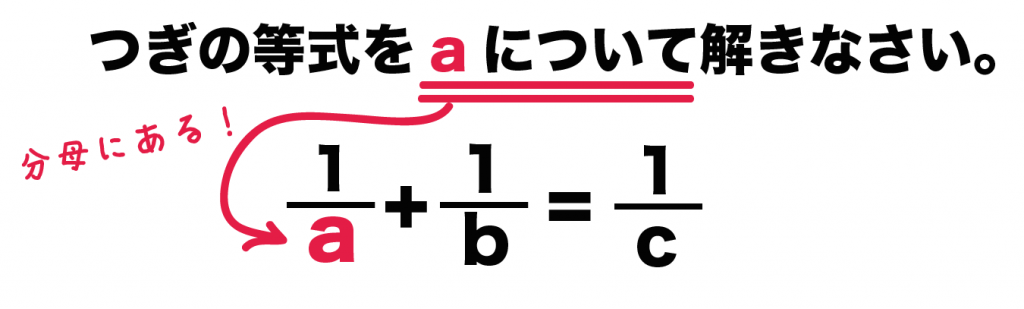
このタイプはつぎの3ステップでとけちゃうよ。
「求める文字」を左辺に、ソレ以外の項を右辺によせちゃおう!
符号に注意して移項しちゃってくれ!
例題の等式では「a」が求める文字だったよね?
だから「a」を左辺に、ソレ以外の項たちを右辺によせてみよう。
すると、
1/a = 1/c -1/b
になるね!
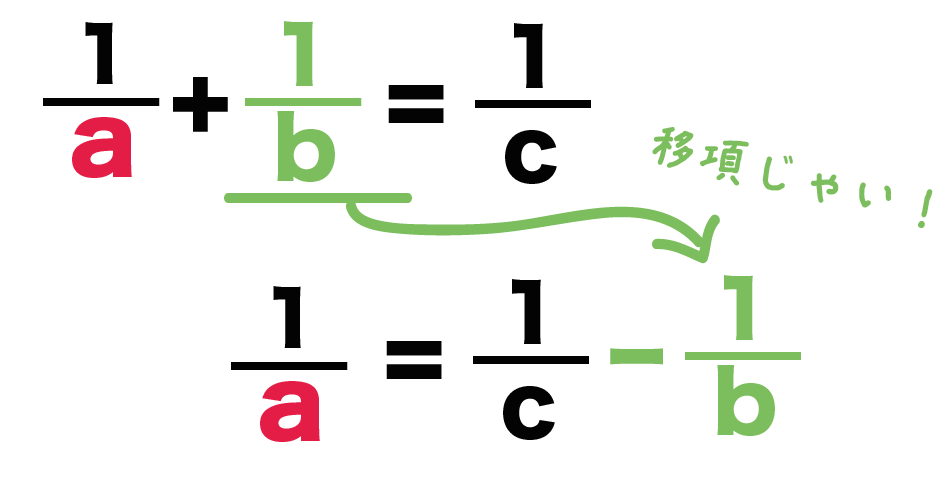
右辺を通分して1つの分数にしてみよう!!
例題でいうと、
1/c -1/b
っていう右辺を通分してやればいいんだね。
えっ。通分のやり方がわからない!?
そんなときは「分数をふくむ文字式の通分方法」を復習してみてね。
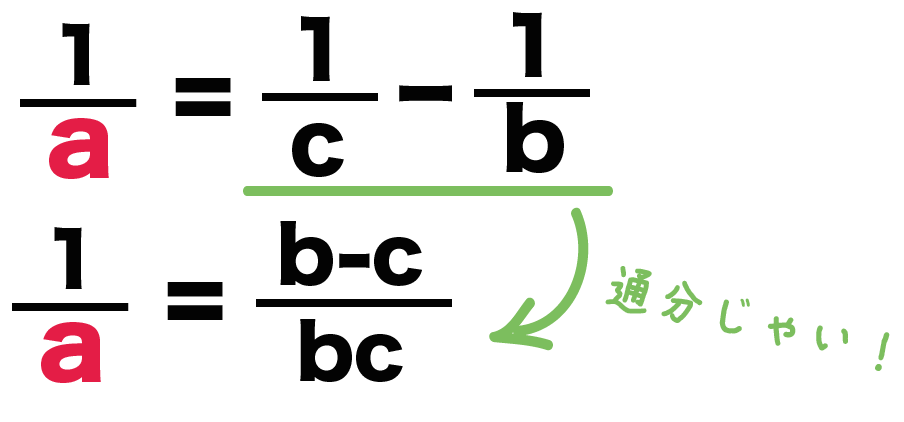
通分してやると、
(b-c)/bc
になるね!
いよいよ最後のステップ。
両辺の分数を逆数にしてあげよう!!
左辺と右辺はそれぞれ1つの分数になっているから、
分子と分母を入れ替えてやればいいのさ。
例題でいうと、
1/a = (b-c)/bc
a = bc/(b-c)
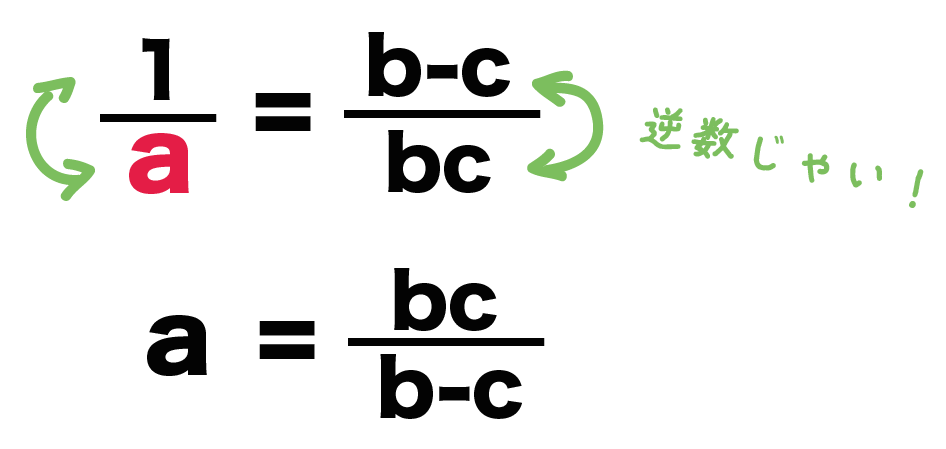
になるね!
これで「通分するパターン」の解き方もマスターしたね。
おめでとう!
分数がふくまれている等式の変形のやり方はどうだった??
をマスターしておけば大丈夫。
きっとテストでいい点とれるはず!本番前によーく復習しておいてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。焼き肉はうまいね。
中2数学のテストでいい点をとるためには、
いろいろな多項式の計算方法
をマスターしておくべきなんだ。
だって、中2数学の基礎的な内容だからね。
多項式の計算の攻略なしにして、中2数学の攻略なし、
ってわけさ。
今日はそんな中2数学のカギをにぎる「多項式の計算」の問題の解き方を
3ステップで紹介していくよ。
よかったら参考にしてみて。
例題をときながら多項式の計算方法をみていこう!
例題:
つぎの計算をしなさい。
2(a+3b+c)-3(2a+5b+3)
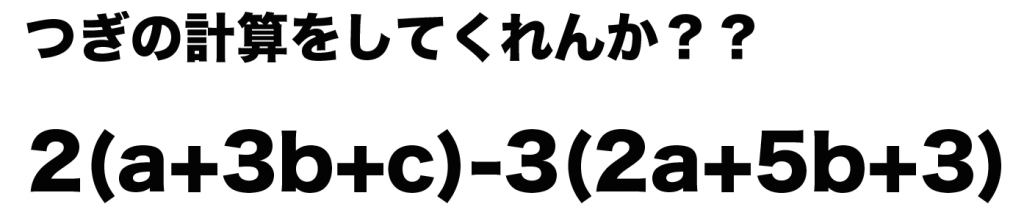
つぎの3ステップでいいんだ。
分配法則をつかって多項式の()をはずしちゃおう!
()がついている多項式ってぽっちゃりしてるっしょ?
だから、こいつをスッキリさせちゃうってわけ。
例題の多項式も()が2つあるよね。
この邪魔くさい()を分配法則ではずしてやると、

2(a+3b+c)-3(2a+5b+3)
= 2a+6b+2c-6a-15b-9
になるね!
−の符号に注意しながら()をはずしてみてね。
スッキリした多項式の中から、
同じ文字の項(同類項)
をみつけてみよう!
aが使われている項、bが使われている項・・・というように文字ごとに洗い出していけばいいんだ。
例題をみてみると、
分配法則でカンタンにした多項式(2a+6b+2c-6a-15b-9)には、
っていう4種類の項があるよね??

こいつらがそれぞれ何個ずつあるかってことを押さえておこう!
さっきみつけた「同じ文字の項(同類項)」の係数を足し合わせてみよう。
あ、係数って文字の前についている数字のことだよ。
例題の多項式では、
という2種類の文字が2つ以上ふくまれていたよね?
ってことはコイツらの係数を足してやればいいわけさ。
すると、
2a+6b+2c-6a-15b-9
= -4a -9b +2c -9

になるね!
これで多項式の計算は終了さ。おめでとう!!
多項式の計算問題は、
っていう3ステップで攻略できちゃうんだ。
これさえ押さえておけば中2数学の基礎はできたようなもんさ。
テスト前にもう一度復習してみてね。
そんじゃねー
Ken