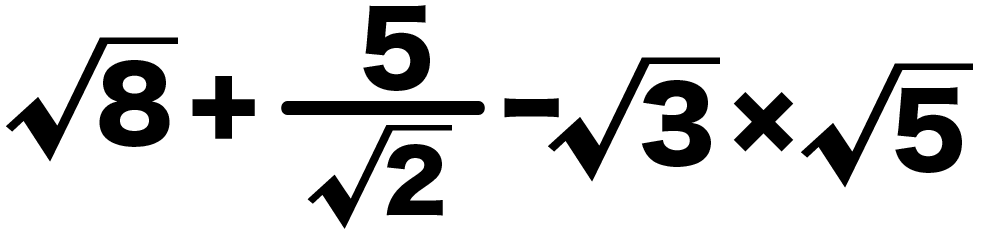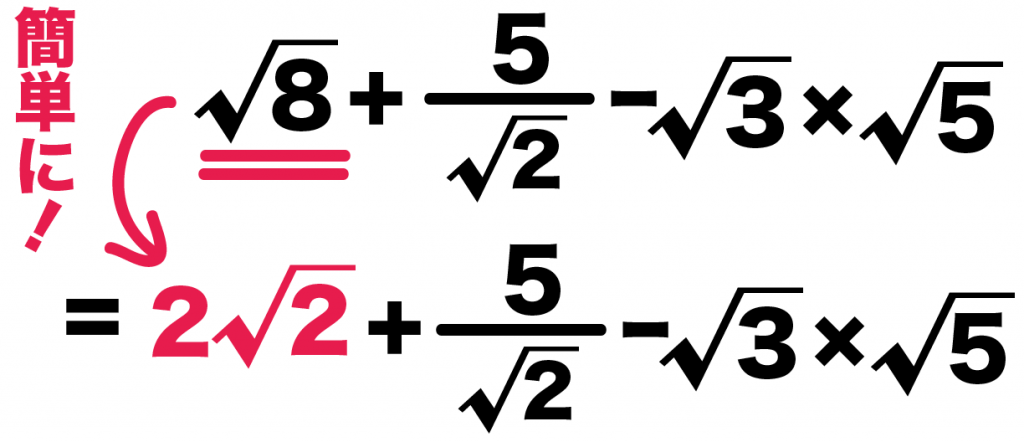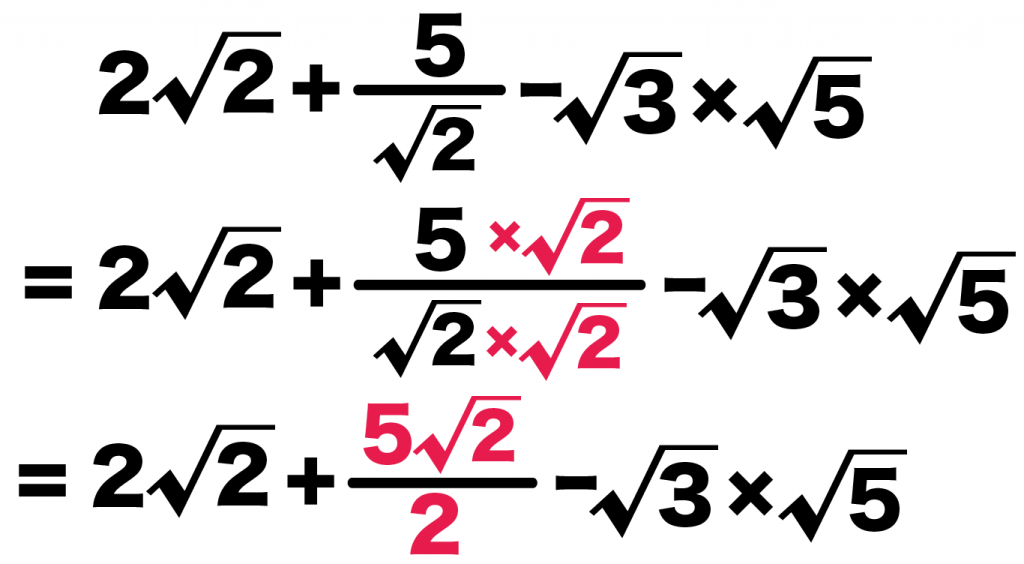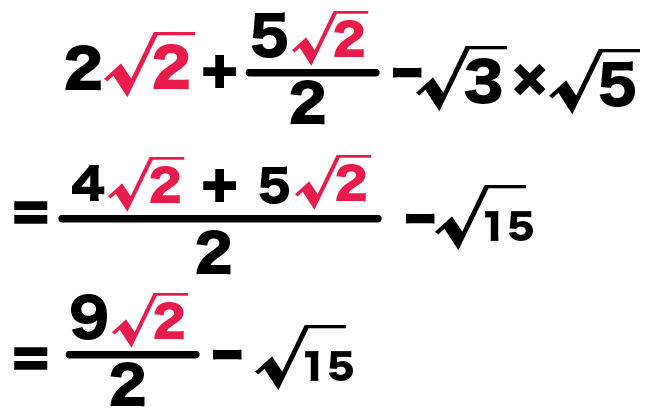平方根・ルートの計算方法・仕方にコツはあるの？？
こんにちは！この記事をかいてるKenだよ。ブルックリンが呼んでるね。
ここまで、平方根の基礎の、
を勉強してきた。
もう、平方根の計算なんてちょれわー
って思ってるよね？？
だけどね、ちょっと待って欲しい。
ルートの計算のミスは忘れたころにやってくるんだ。
そこで今日は、
ルート・平方根の計算方法のコツ
をおさらいしよう。
ガンガン復習しておこうぜ。
ルート・平方根の計算方法・仕方の3つのコツ
ルート計算のコツはつぎの3つだ。
- ルートを簡単にする
- 足し算・引き算はべつもの
- 分母は有理化しとく
練習問題をといてみよう。
つぎのルートの計算をしてください。
√8 + √2分の5 – √3 × √5
コツ1. 「はじめにルートを簡単にする」
まず、
ルートを簡単にできるかどうか
をみてみよう。
もし、ルートを簡単にできそうなら一番先にやっちまおう。
なぜなら、
整数と平方根にわけて計算できるようになるからね。
例題をみてみると、
いちばん左の「√8」を簡単にできそうだ。
なぜなら、中身の「8」には「2の2乗」がはいってるからね。
こいつを外にだせるわけだ。
ルートを簡単にすると、
√8 + √2分の5 – √3 × √5
= 2√2 + √2分の5 – √3 × √5
になるね。
☆ルートを簡単にする方法をわすれたら復習しよう☆
コツ2. とりあえず分母は有理化しとく
ルートの計算に分数がある？？
そういうときは、分母を有理化しちゃおう。
分母からルートを消せばいいのさ。
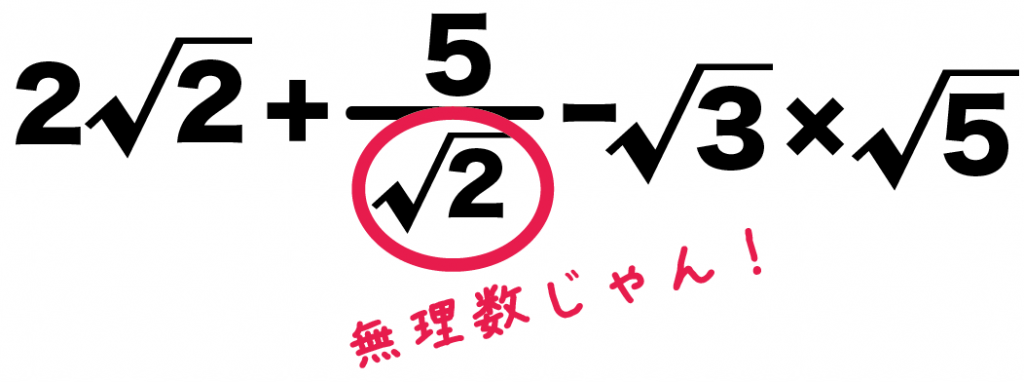
例の計算式では、
√2分の5
の分母に平方根がはいってるね。
この「√2」を分母から消したい。
そんなときは、分母・分子に√2をかければよかったね？？
すると、
2√2 + √2分の5 – √3 × √5
= 2√2 + 2分の5√2 – √3 × √5
になる。
分母の有理化をしておくと、
ルートの計算する余地があるのかどうか？？
がハッキリするんだ。
余地があるんなら、ルートの計算を続行すればいいし、
ないんなら計算をやめればいい。
めんどいけど、分母の有理化はやっておこう。
コツ3. 「足し算と掛け算はべつもの」
ルートの計算の最大の特徴。
それは、
足し算・引き算
と
掛け算・割り算
がまったく違うってことだ。
つぎの計算のルールを覚えてほしい。
- 足し算 / 引き算 ⇒ ルートの中身がおなじ項の整数だけ計算
- 掛け算 / 割り算 ⇒ ルートの中身を掛け算、割り算する
例題ではいったん掛け算をしちゃおうか。
右の項の、
– √3 × √5
が計算できそうだ。
平方根の掛け算では「√の中身」を計算してもよかったよね？？
だから、
– √3 × √5
= – √15
になるね。
あとは左の足し算。
- 2√2
- 2分の5√2
はルートの中身が2で一致してる。
整数部分を足し算してやると、
2√2 + √2分の5 – √3 × √5
= 2√2 + 2分の5√2 – √15
= 2分の9√2 – √15
になるね。
これでルートの計算は終了だ。
まとめ：ルートの計算方法のコツは3つしかない
ルートの計算はどうだった？？
計算のコツは3つのみ。
- 最初にルートを簡単にする
- とりあえず分母は有理化
- 足し算と掛け算はまったくべつもの
ルートの計算問題をといて慣れていこう！
そんじゃねー
Ken
↓↓ルート計算のコツを動画にまとめてみたよ↓↓
