二次関数の変域を求める問題の解き方の3つのコツ
二次関数の変域を求める問題って??
ある日、数学が苦手なかなちゃんは、
二次関数の変域の問題に出会いました。

関数y=x²について、xの変域が -2≦x≦4 のとき、yの変域を求めなさい。

二次関数の変域・・・・?
変域って、
聞いたことあるな。。
でてきたもんね。
でも、
今回は2次関数。。
なんか違う気が・・・
おっ、
いいところに気づいた!
二次関数の変域のナゾ
を解き明かしていこう!
一次関数と二次関数の変域の違うところ?
一次関数の変域って覚えてる?
わ、わすれた!!
二次関数の変域は違うの?
そう!
yの最大・最小値が
xの変域の端にならないことがある!!
へっ!?
なんで??
それは、
グラフの形に秘密がある。
たとえば、
この二次関数のグラフ
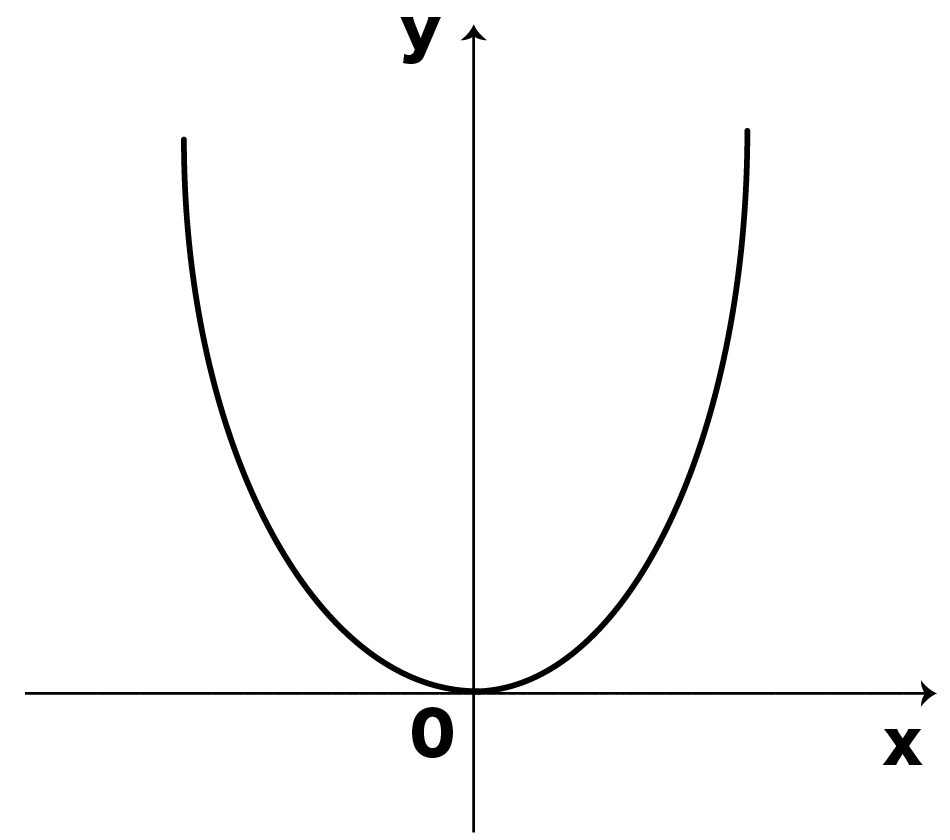
y軸に左右対称だ!
1次関数のグラフとの違い
分かったかな?
はい!
このグラフだと、
yが0より小さくなること
はないですよね!

そう!
じゃあ、
比例定数の正負が
グラフにどう影響あたえる??
一次関数だと、
比例定数の正負によって、
右上がり、
右下がりだった!
うん。
じゃあ、二次関数はというと、
↓を見比べてみて!!
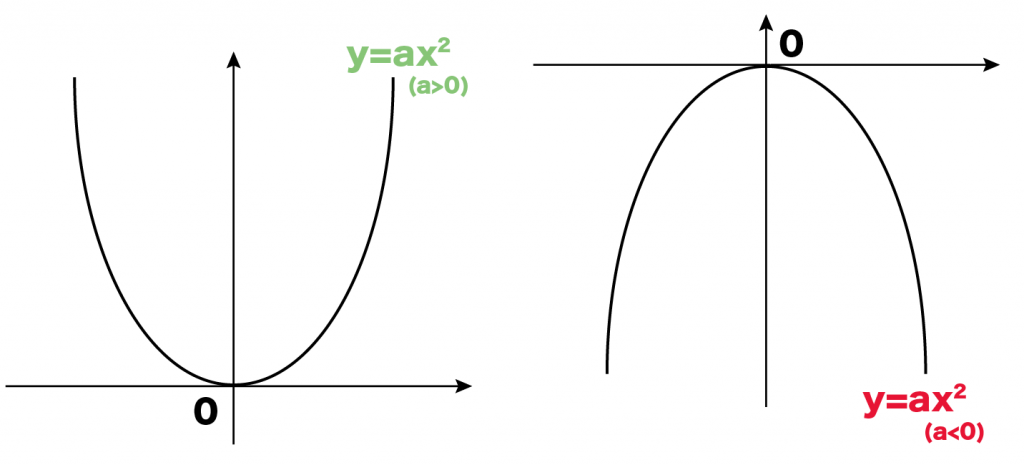
yの変域が特殊。
0で一番小さいときと、
0が一番大きいときがある!!
よく気が付いた!
二次関数の変域の問題の求め方3つのコツ
こっから本番!
練習問題をといてみよう。
関数y=x²について、xの変域が -2≦x≦4 のときのyの変域を求めなさい。

コツ1. 「比例定数aの正負の確認」
y=x²
の定数aは正負どっち?
aは1!
ってことは、
「正」だ!
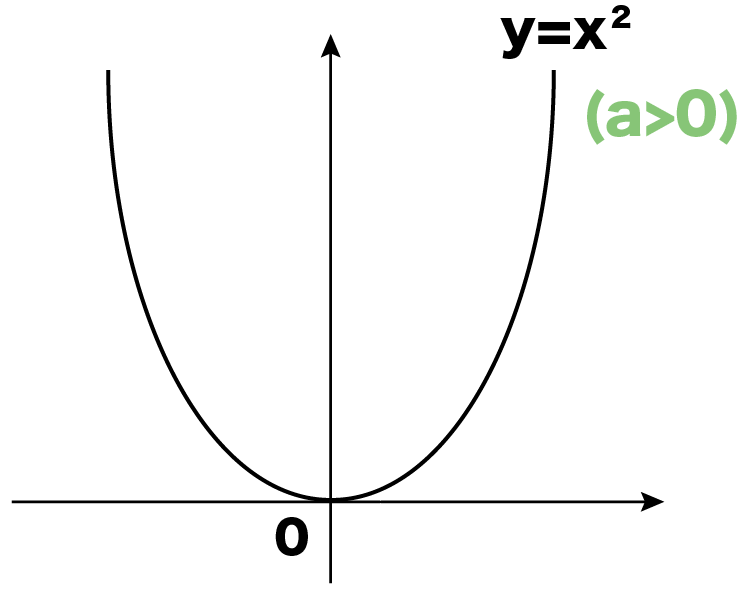
そう!
簡単でも確認は大事
コツ2. 「xの変域に0が入るか
xの変域に、
0が入るかどうか
を確認すること。
これ、大事!!
なんでかって、グラフを見て!
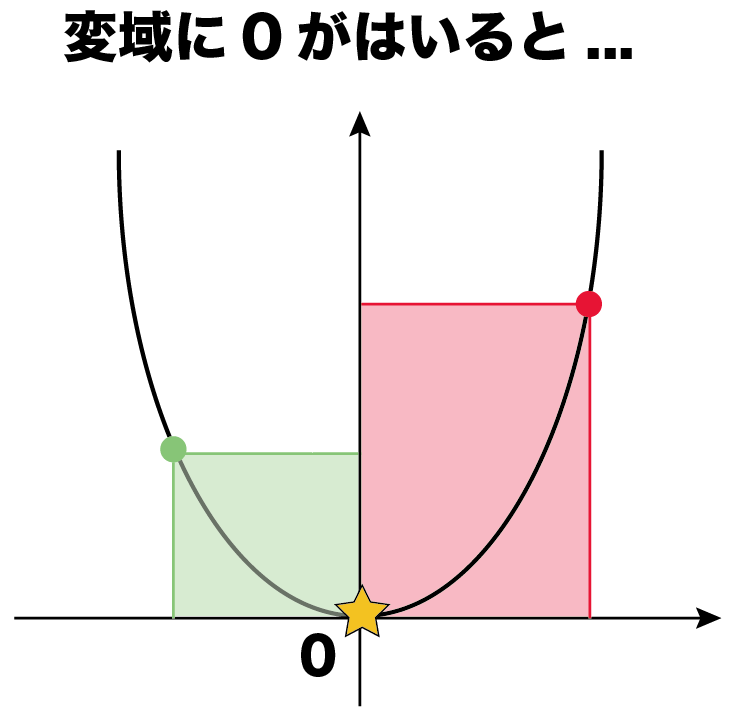
xの変域に0が入るとやばい。
yの変域の最小が0になる!
そう!
さっきの問題の変域、
「-2≦x≦4」
には0はいってる??
入ってる!
コツ3. 絶対値が大きいXを代入
絶対値が大きいほう
だよ。
念のため確認。
-2と4、
絶対値が大きいのは?
どっちだっけ・・・・・・
絶対値は、
正負関係なく、数字が大きいほど大きい
よ!
ってことは、
4だ!
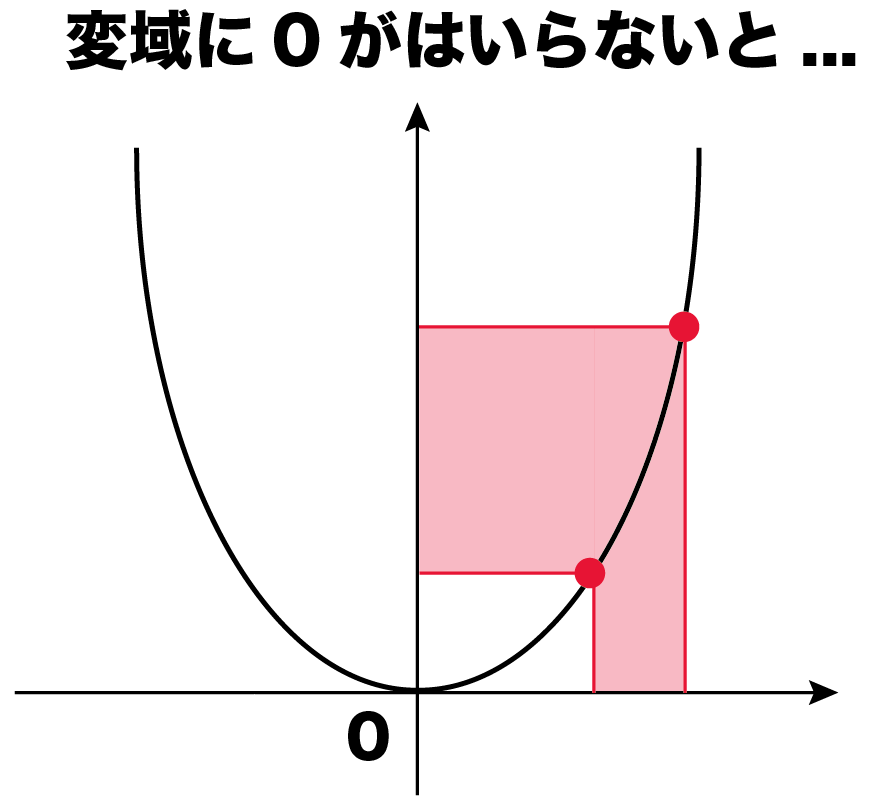
xの変域に0がふくまれるときは、
絶対値が大きいxを代入する
って覚えよう!
はい!!
さっそく代入してみます。
絶対値が大きいxは4。
y=x²に代入すると、
4×4=16になる。
yの変域は、
0≦y≦16かな!
二次関数の変域とけてるじゃん!
やっっったーあーーー!
まとめ:二次関数の変域の問題はグラフをかくのが一番楽!
二次関数の変域のポイントは、
グラフをかくこと。
これにつきるね。
グラフだと
わかりやすかった!!
でしょ??
ここまでをまとめるよ。
【定数aの正負】→【xの変域に0が入るか】→【代入は絶対値が大きいほう】
変域が求められるといいね!
が、がんばります!
練習問題つくったよ!
解いてみよう!
【1】y=2x²において、
- -2≦x≦4のときのyの変域
- 1≦x≦5のときのyの変域
【2】y=-x²で、
- -3≦x≦6のときのyの変域
- -3≦x≦-1のときのyの変域
ありがとうございます!




