高校数学でも関数を勉強していくんだが、1つ、新しい言葉が登場するぞ。
それは、
象限（しょうげん）
だ。
ズバリ、
座標平面の場所の名前のこと
さ。
人間の身体にも「頭」とか「首」とか「肩」とか「腰」とか、パーツに名前がついてるだろ？？
それと同じように、座標平面のスペースにも名前がついている、ってわけよ。
たとえば、次のように$x$軸と$y$軸がある座標平面があったとしよう。
右上のスペースを場所を「1」。
そこから反時計回りに「2、3、4」と番号をつけるんだ。それぞれ、
- 第1象限
- 第2象限
- 第3象限
- 第4象限
という名前がついているぞ。
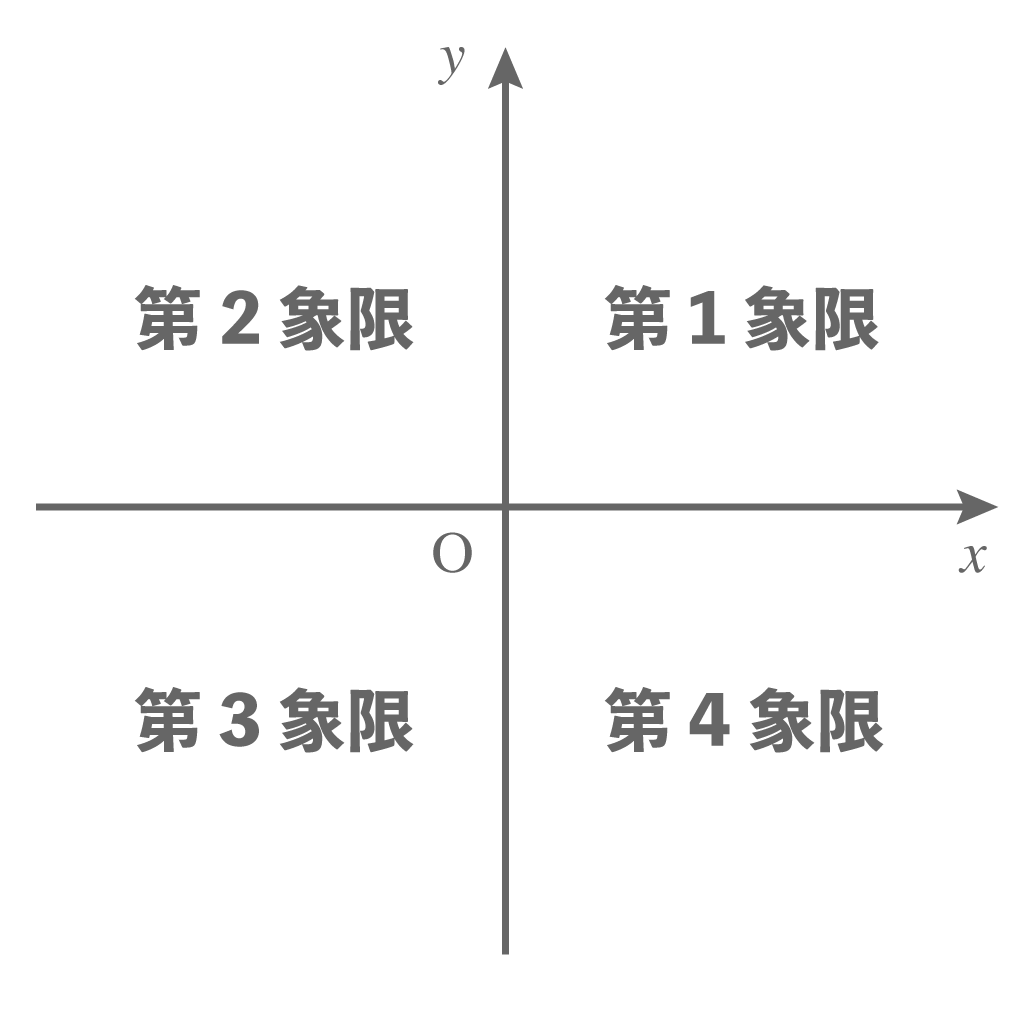
この象限を使えば、
どこにある座標があるのか説明できるから便利だよな。
かりに、ここにとある座標の点があったとする。
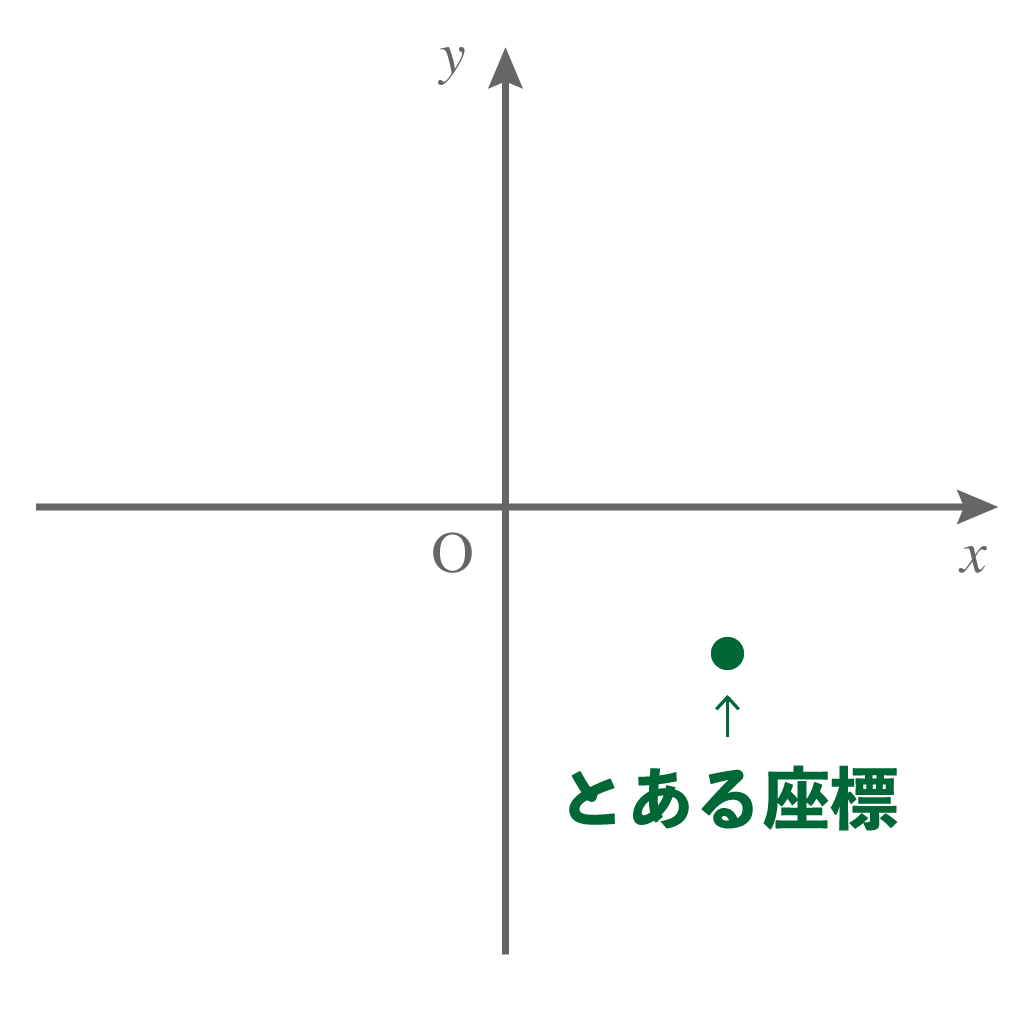
象限をマスターしていないと、
えっと、この右斜め下ら辺にあるこの点は・・・・
とオドオドしながら説明しねえといけねえな。
でもさ、象限をものにしておけば、
この第4象限にある座標は・・・・
と堂々と胸張って言えるはずだ。
どうだ、かっこいいだろう？
座標平面の「軸上の点」は象限には含まれない！？
ここで疑問になってくるのが、
座標軸上の点の扱いだよな。
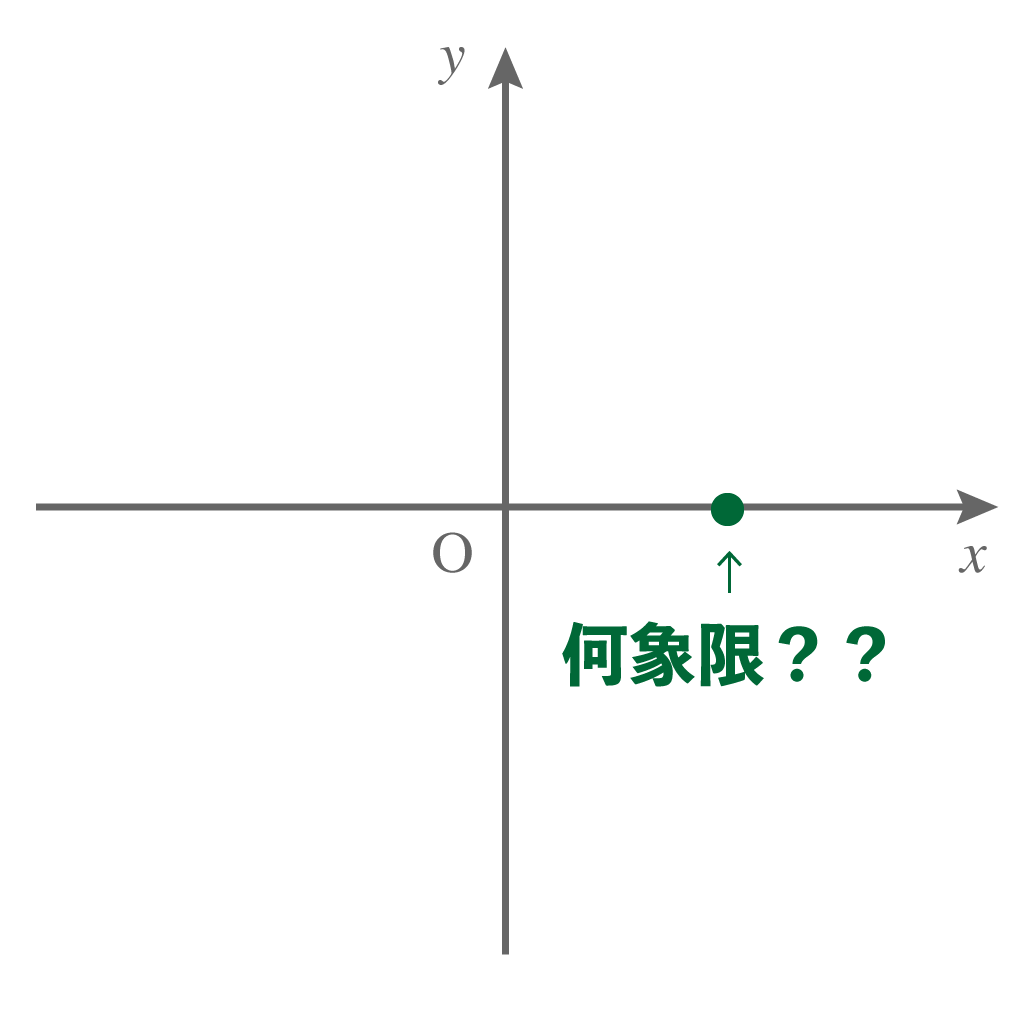
象限の境界ともいえる$x$軸・$y$軸上にある座標はどの象限に属しているんだろう？？
じつは、ぶっちゃけ、
$x$軸$y$軸の軸上にある座標は象限には含まれない！
第1象限でもないし、第2象限でもないし、第3でも第4でもない。もちろん、第5象限でもない、ってわけさ。
座標平面の象限の覚え方象限の順番と名前の覚え方
オッケー、だいぶ象限について詳しくなってきたな。
象限のポイントは次の2つだ。
- 右上のスペースを「1」とする
- 反時計回りに番号を数える
でもさ、これ覚えられるか？
なぜ、座標平面の右上の場所が1なのか？
で、なぜ、反時計回りに番号が続くのか？
別に時計周りでもいいはずだし、いや、むしろランダムだっていいじゃないか。
そんなお前らのために、とっておきの象限の覚え方を伝授するぞ。
象様の助けを借りるんだ。
「象限」という言葉の１文字目は「象」様だろう？？
その象様をな、座標平面の軸の矢印の向きに招待しよう。
神々しいお方だからくれぐれも懇切丁寧、丁重に振る舞えよ。
次は象様の「目の位置」に注目してくれ。
お目目の位置が第1象限
と覚えよう。
象様の目は右上にあるから、座標平面の右上の場所が第1象限になりそうだな。
さて、ここで時を進めるぞ。
その象様が鼻を上げるシーンを想像してくれ。
象様は水浴びするとき、鼻を上にあげるよな？？
そのとき、象様はどっち周りに鼻をあげたか？？
そう、反時計回り、だよな。
決して、右向きの状態では、時計周りに鼻は上げられないはずだ。
ゆえ、お目目の位置を「1」として、反時計回りに数を数えて象限の名前にするってことよ。
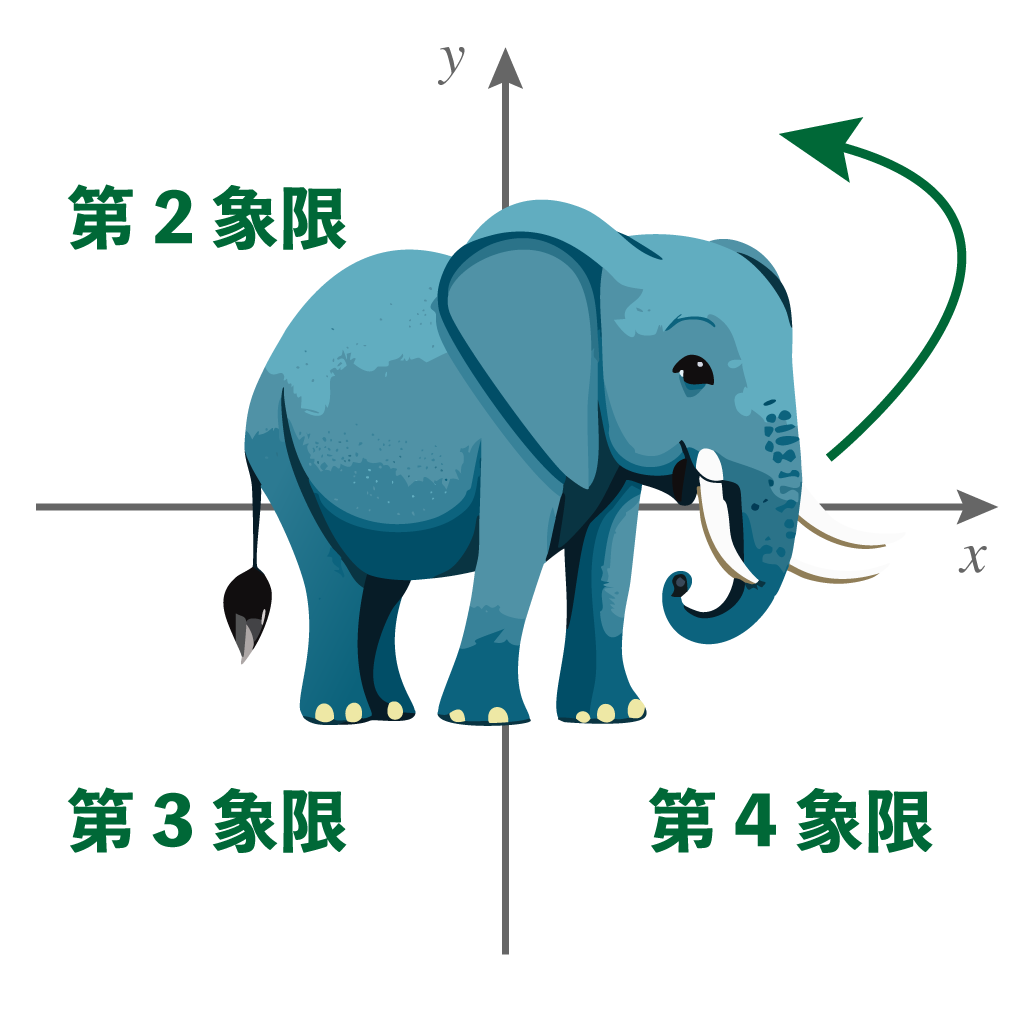
こんな感じで、象様の力を借りれば、
- 象限の開始場所
- 番号の進む順番
を覚えられるはずだ。
新しい言葉の「象限」にしっくり来たか？？
それじゃあなぁ！
