3分でわかる！二次関数の平行移動の公式〜なぜあそこがマイナスになるのか？〜

クマシロ

よう、消しゴムの妖精のくましろだ。

関数のグラフの点を全て同じ方向に移動させること

を

平行移動

っていうんだ。

で、高校数学では二次関数をガンガン平行移動させていくぞ。

ありがたいことにな、二次関数のグラフの平行移動には公式が用意されている。声出して喜んでもいいぞ。

公式

放物線の二次関数の $y = a x^{2} + b x + c$ を $x$ 方向に $p$ 、 $y$ 方向に $q$ 平行移動させたら、放物線の式は次のようになる。

$y - q = a (x - p)^{2} + b (x - p) + c$

早速この公式を使ってみるぞ。

例えば、

$y = 3 x^{2} + 5 x + 7$

という二次関数を $x$ 方向に-3、 $y$ 方向に1、平行移動させてみよう。

さっきの公式でいえば、

$p = - 3$
$q = 1$

っつうわけだ。よって、公式を使って平行移動した放物線の式は次のようになる。

$y - q = 3 (x - p)^{2} + 5 (x - p) + 7$

$y - 1 = 3 (x + 3)^{2} + 5 (x + 3) + 7$

$y = 3 (x^{2} + 6 x + 9) + 5 x + 15 + 7 + 1$

$y = 3 x^{2} + 18 x + 27 + 5 x + 23$

$y = 3 x^{2} + 23 x + 50$

なぜ二次関数の平行移動の公式が使えるの？

さっきの公式を使えば、どんな二次関数でも平行移動できそうなことがわかった。

だけどよ、なんであの公式が使えるんだろうな？？

なぜ $p$ を引かなきゃいけないのか？？

むしろ、直感的にはたしてやりてえぐらいだしさ。

そんな疑問も冷静に考えれば解けるぞ。

例えば次のように考えてみよう。

$y = f (x)$ で表される関数があったとする。

この関数のある1つの点を

$(x, y)$

としよう。その点をx方向にp、y方向にqだけ平行移動させた点を

$(x^{'}, y^{'})$

とする。

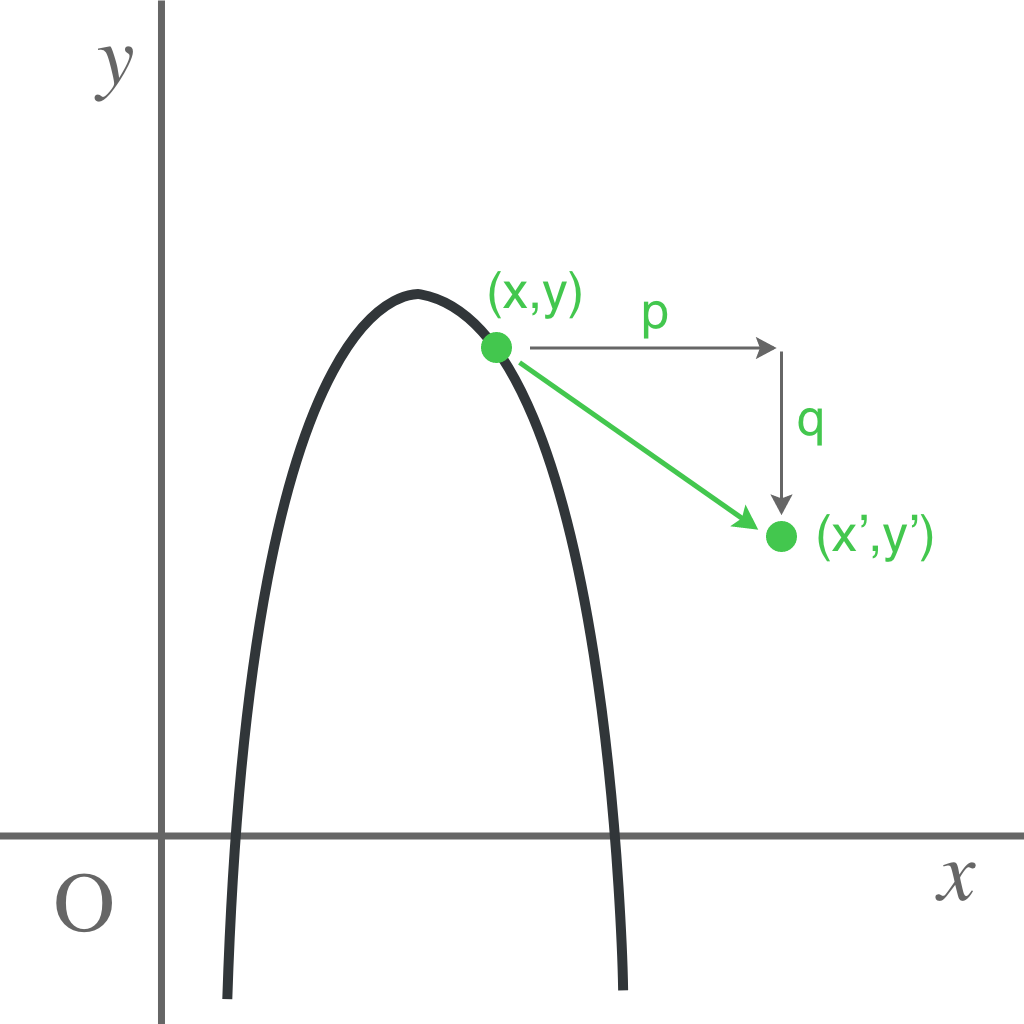
冷静に考えてみると、移動した点の $(x^{'}, y^{'})$ というやつは、 $x$ 座標は $x + p$ になって、 $y$ 座標の $y^{'}$ は $y + q$ になるよな。

だから、

$x^{'} = x + p$
$y^{'} = y + q$

になる。こいつを $x と y$ について等式変形してみるぞ。

$x = x^{'} - p$
$y = y^{'} - q$

この新しい $x と y$ を元の関数 $y = f (x)$ に代入してみよう。

すると、次のようになる。

$y = f (x)$

$y^{'} - q = f (x^{'} - p)$

になる。すると、どうだ？？　新しく平行移動した $x^{'}$ と $y^{'}$ で関数が表せているな。

$y = f (x)$ という関数を $x 方向に p 、 y 方向に q$ だけ平行移動させた関数は

$y - q = f (x - p)$

になるわけだ。

二次関数の $y = a x^{2} + b x + c$ を $x$ 方向に $p$ 、 $y$ 方向に $q$ 平行移動させたら、yの代わりに「y-q」、xの代わりに「x-p」を入れてやればいい。

よって、

$y - q = a (x - p)^{2} + b (x - p) + c$

になる！

二次関数の平行移動の公式をマスターしたな？

クマシロ

次は二次関数の対称移動の公式を習得していこう。

それじゃあな！