折り返した図形の角度を求める2つのコツ
図形が折り返しちゃってるんだけど・・・?
中学数学では「角度を求める問題」が出てくるけど、中でも厄介なのが
図形が折られちゃっているパターンだ。
例えばこんな感じの問題↓
長方形の紙を次のように折りました。角度xを求めなさい
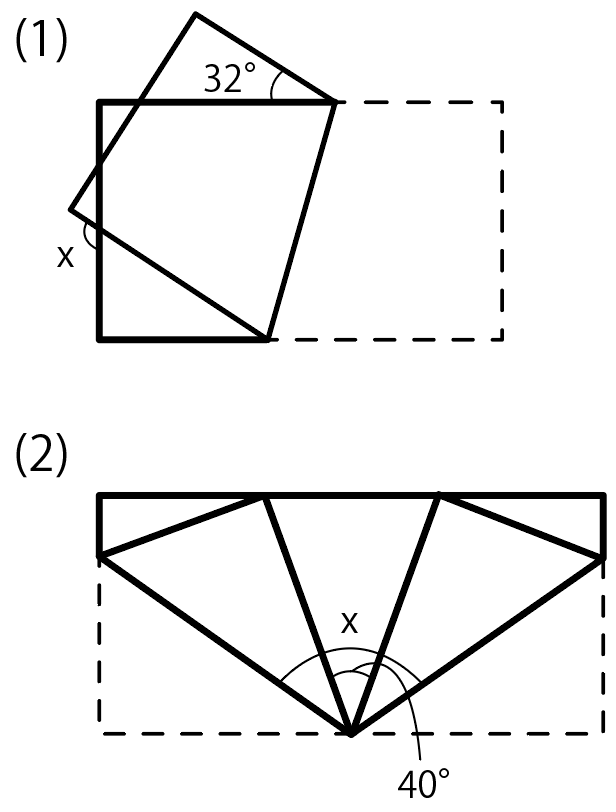
じつは、図形の折り返しの問題もカンタン。
2つのコツを知っていれば解けるようになるよ。
コツ1. 折り返しても「長さ・角度」はそのまま
図形を折り返ししても、
元の図形の「長さ」や「角度」は変わらない
ことが大原則。
つまり、
折る前の図形
と
折られて移動した図形
はまったく同じってことだね。
たとえば、この三角形を
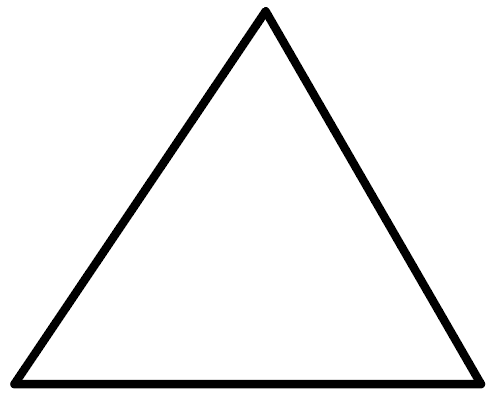
こんな感じでおったら、
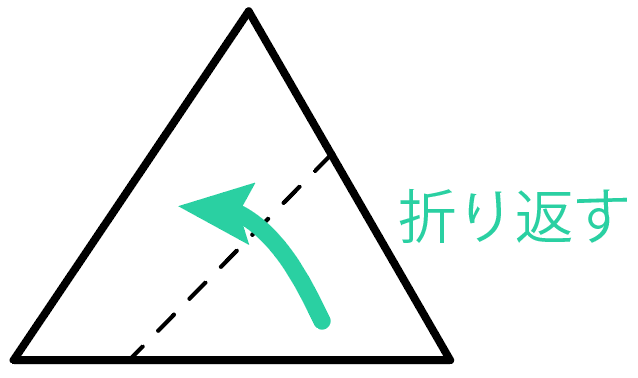
こうなって、
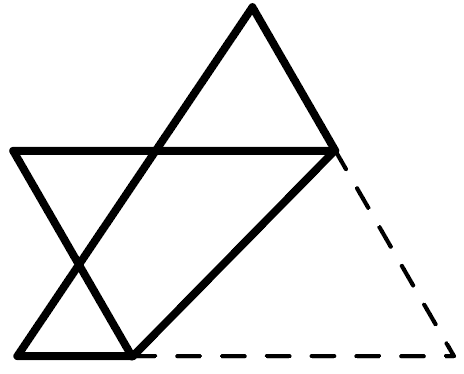
AとBはまったく同じ三角形ってわけ。
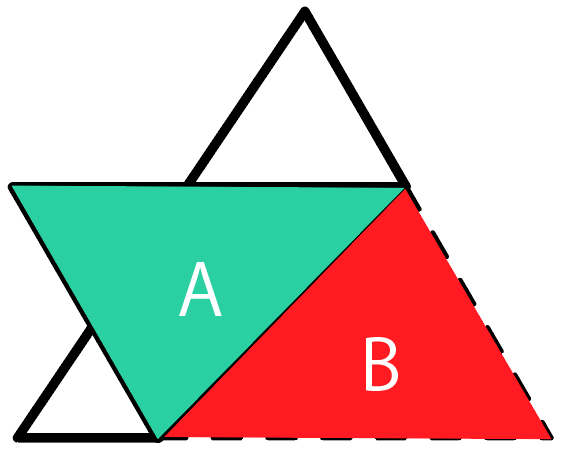
業界用語でいうと、2つの図形は「合同」といえるね。
合同であることから、
折り返して移動しても「辺の長さ」や「角度」は変わらない、と言えるんだね。
なぜなら、合同な図形は対応する角度、
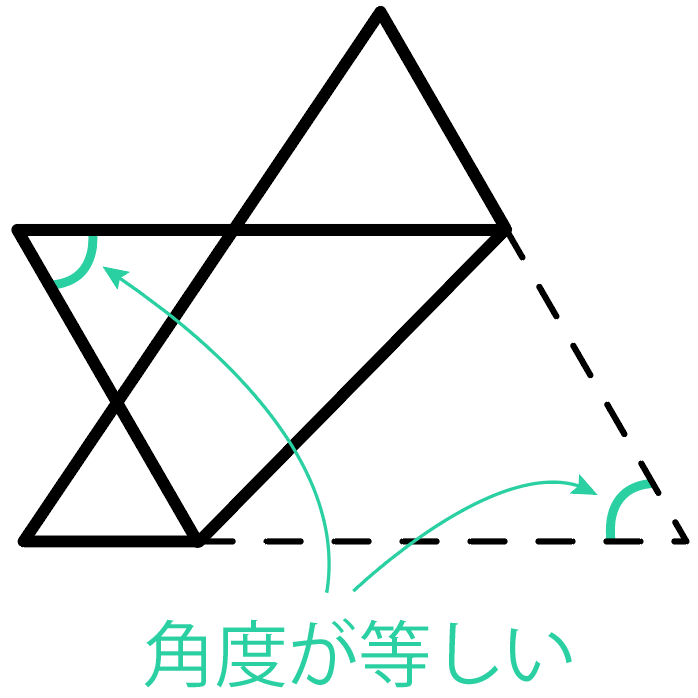
辺の長さがそれぞれ等しいっていう性質があるからだ。
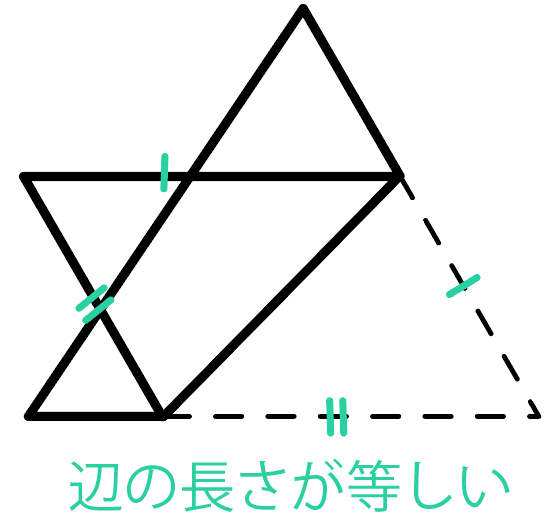
詳しくは「合同な図形の性質」を復習してみてね。
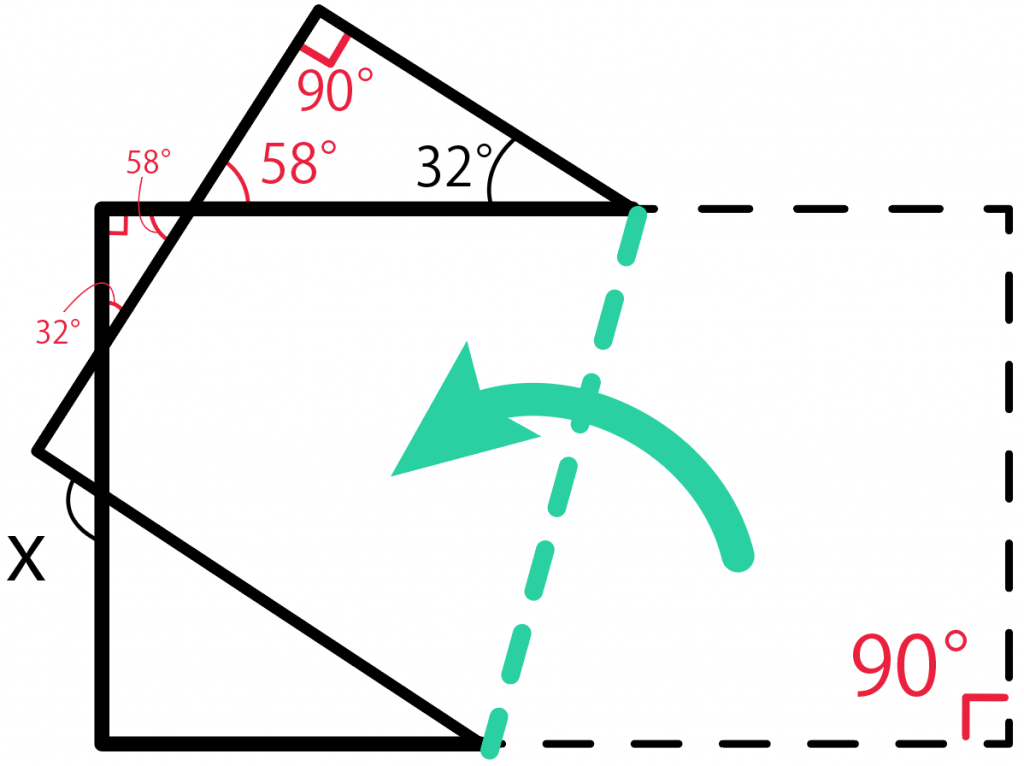
ここで1つ目の図形を見てみよう。
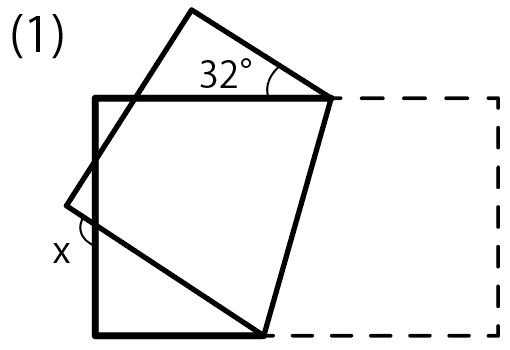
ここが折り目になっていて、
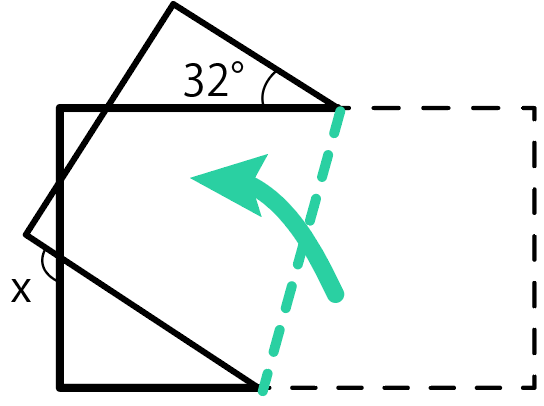
右下の四角形(台形)が左上に移動したわけだ。
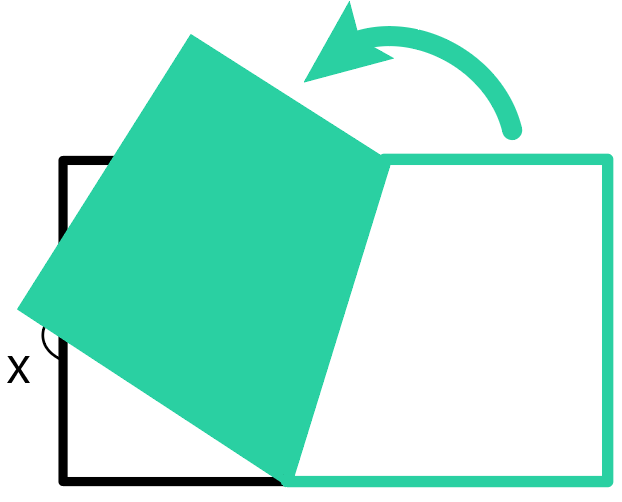
「折る前の図形」と「移動した実線の図形」は合同。
つまり、長さや角度はそのままだから、角度がすでにわかってるところがあるね。
左上の角度は90度。
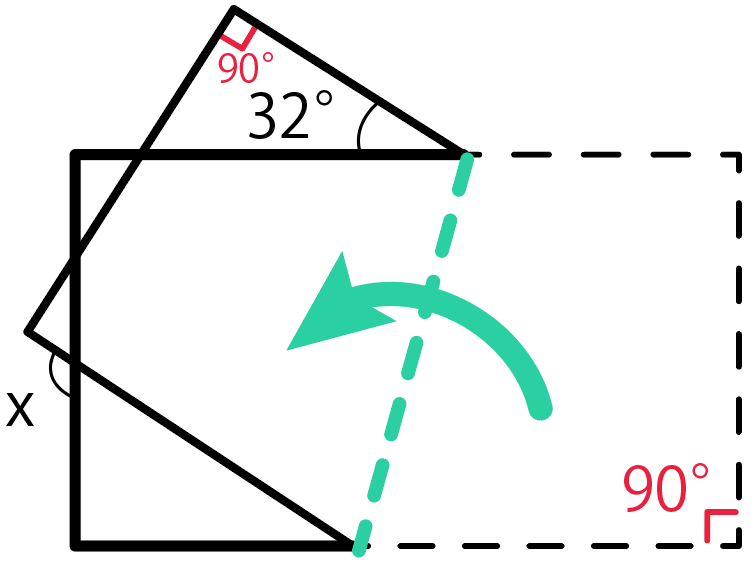
そして、三角形の内角の和は180度だから、180から90と32を引いて、
180 – 90 – 32
= 58
となって、残りの内角で58度。
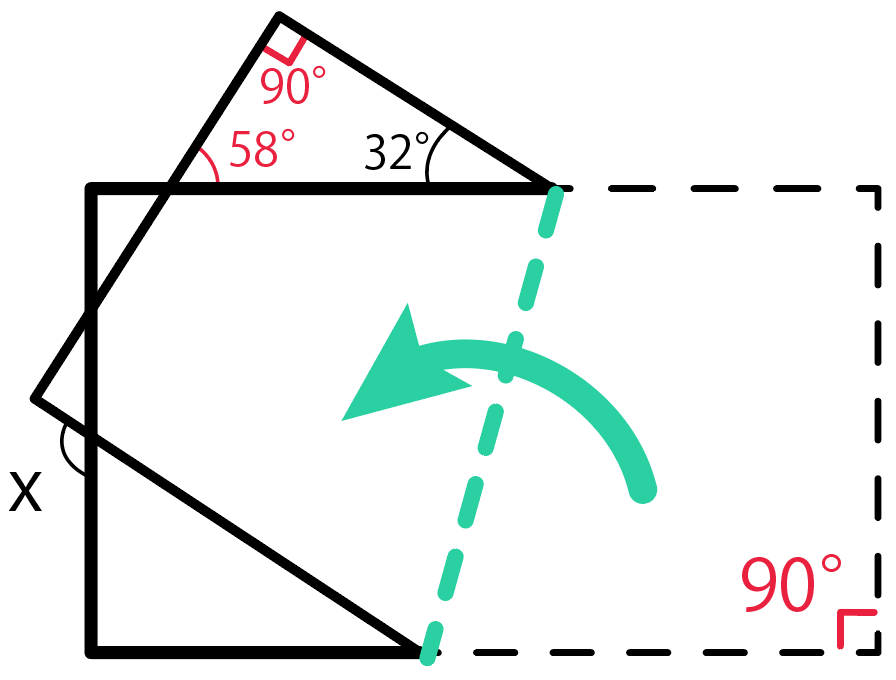
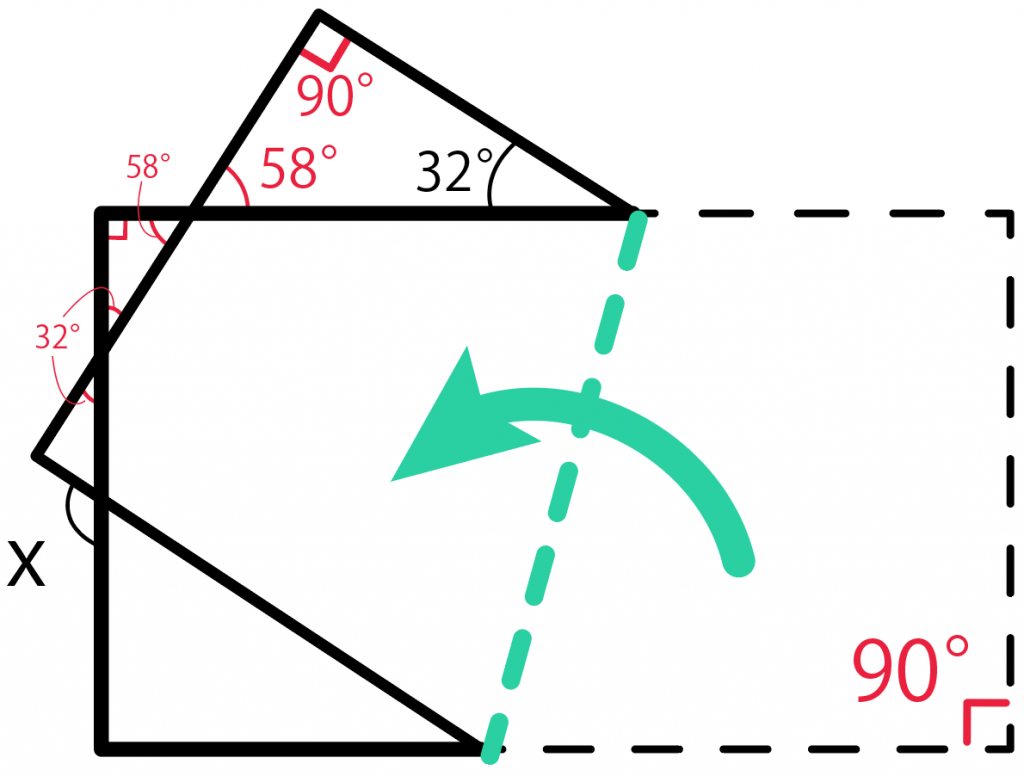
さらに対頂角を使って、小さい三角形の内角の1つも58度。
三角形の内角の和は180で、1つが直角90度だから、残りは32度。
で、さらに小さな三角形で対頂角を使う。
あとはミニ三角形で「外角の性質」を使って
90 + 32
=122
で、xは「122度」になるはず。
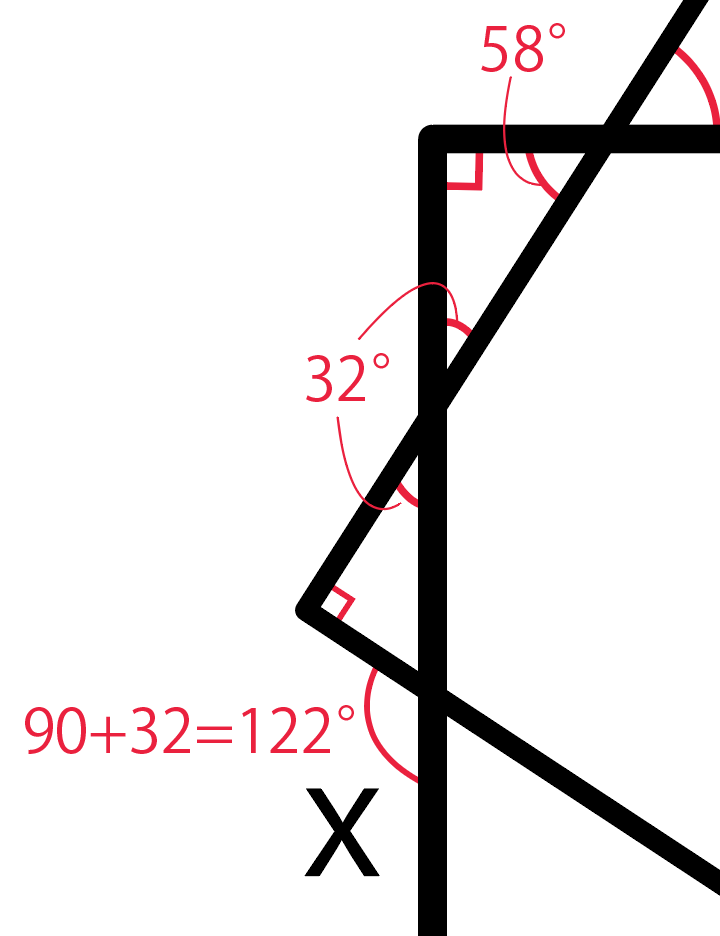
こんな感じで、
折り返しても長さや角度が変わらない
と知っておけば、折り返しの問題も解けるはずだよ。
その2. 折り目は「角の二等分線」
さっきのことを応用してやると、図形の折り目は「角の二等分線」になってるはずだ。
なぜなら、折る前と折った後の図形が合同だからだね。
2つ目の例題を見てみよう。
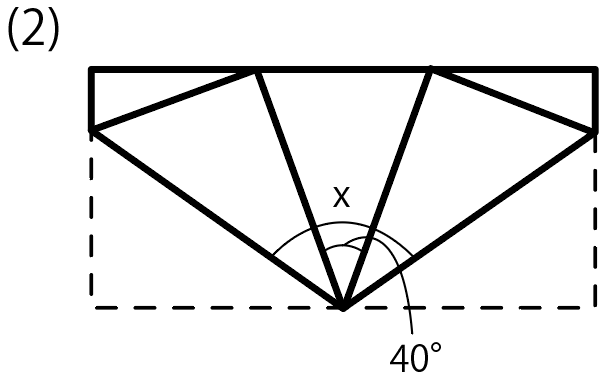
この図形は2箇所で折られていて、折り目が2箇所ついているね。
折り目が「角の二等分線」であることを使うと、
折り目を挟んでいる角度が等しい
ことになる。
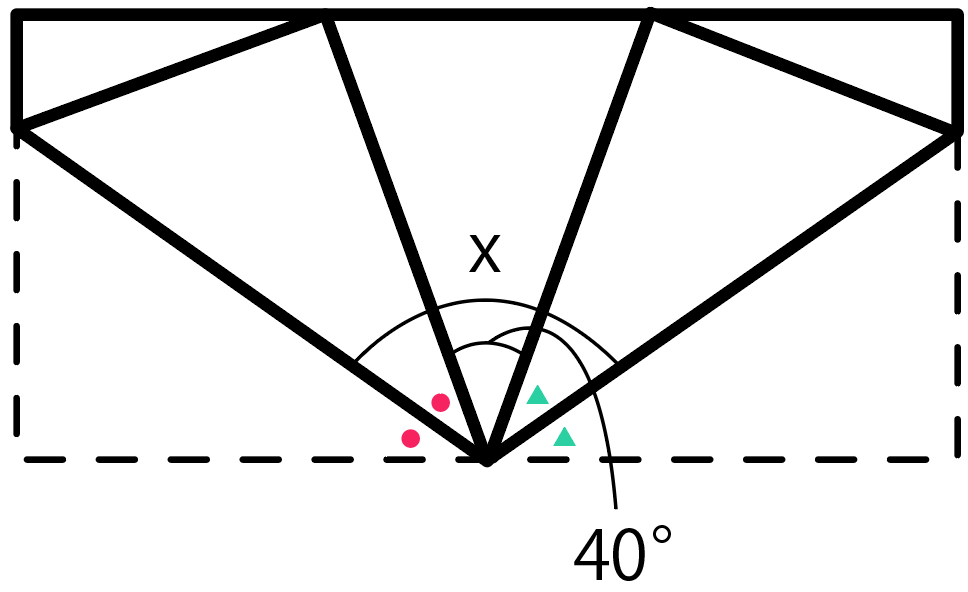
それぞれa、bと置いてやると、
2a + 2b + 40 = 180
っていう方程式が作れるね。
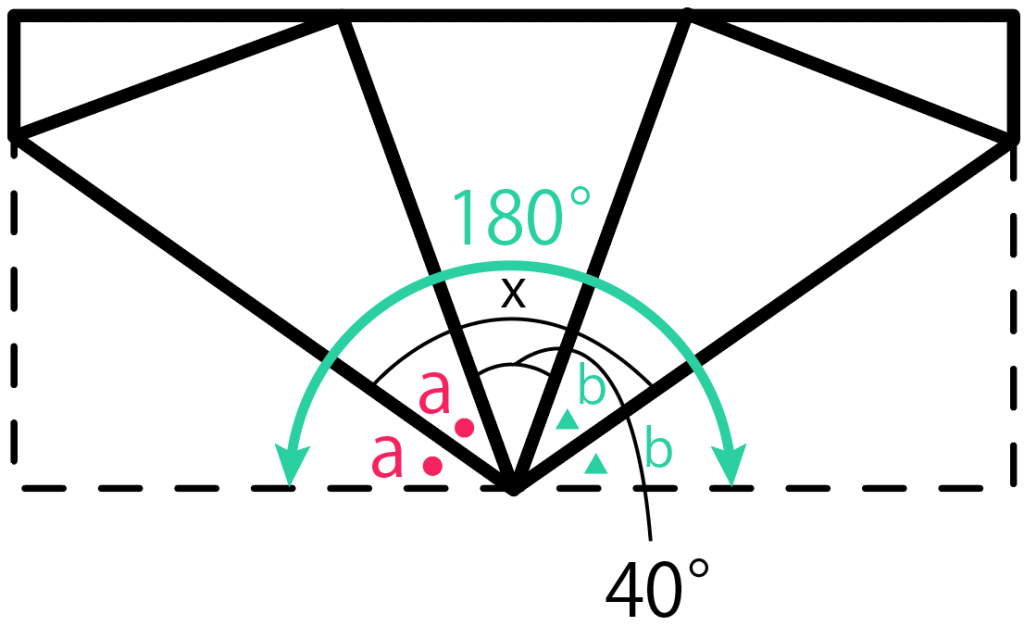
「 a + b 」について解いてあげると、
2a + 2b + 40 = 180
a + b = 70
ってなる。
この問題ではラッキーなことに、
角度 xは「a とbを足したもの」に「40度」を加えたものだ。
よって、「a + b + 40」がxになるはずだね。
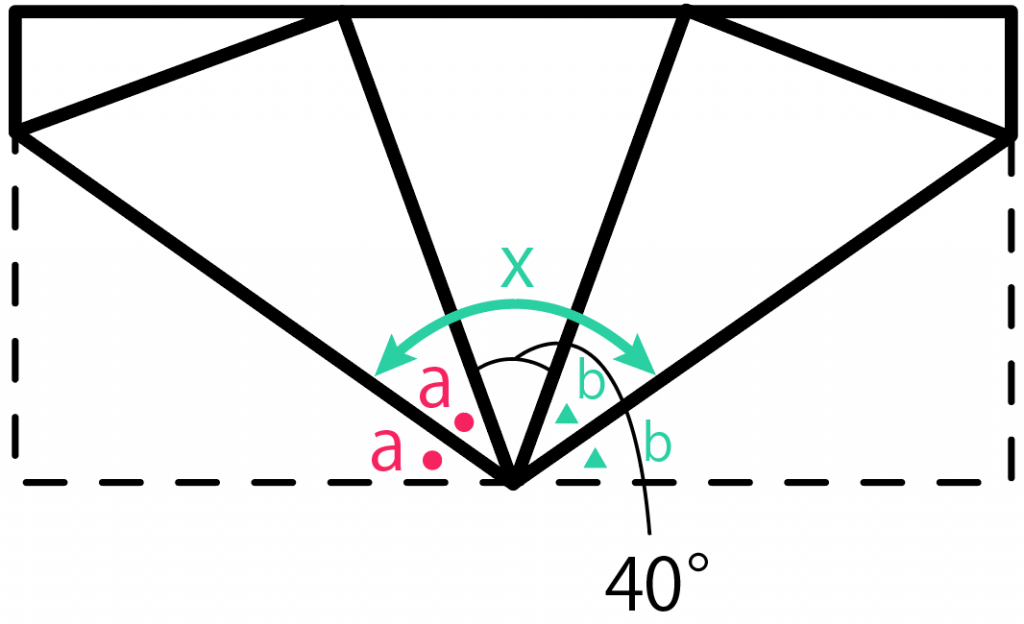
ってことで、「a + b + 40」を計算してみると、
a + b + 40
=70 + 40
= 110
と出てくる。
つまり、xは110度ってわけ。
こんな感じで、図形を折り返している角度の問題は、
- 折り返しても角度や長さは同じ
- 折り目は角の二等分線である
さえ知っていれば大丈夫。
ガンガン問題を解いていこう。
そんじゃねー
Ken





