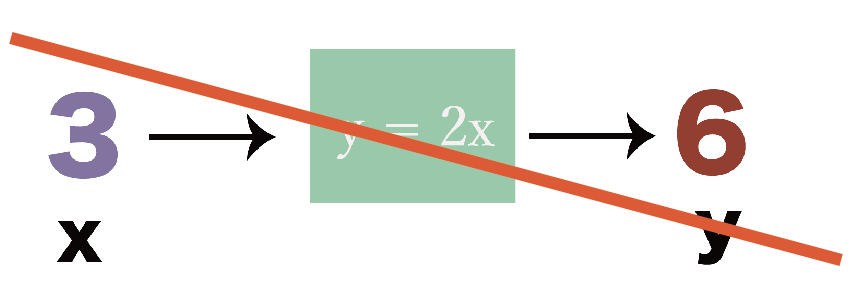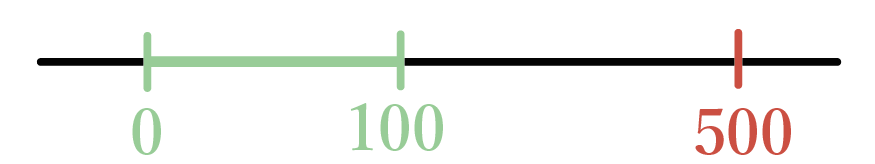【中学数学】関数の「変域」ってなんだろう??
中学数学でならう関数の変域がヤッカイ!!
こんにちは、この記事を書いているKenだよ。まんじゅうを食べたい。
関数を勉強するって大変だよね??
「関数の意味」とか「変数」とかの用語をおぼえなきゃいけないからさ。
※ 関数の意味がわからないときは「関数とは??」という記事を参考にしてくれ。
その「関数」の用語の中でもヤッカイなのが
「変域(へんいき)」
という言葉だ。変域ってまちがいなく日常生活ででてこない単語だし、ちょっと怪しいよね??。

そこで今日は、
関数の変域とはなにか??
ということを説明していくね。
関数の変域ってなんだっけ??
関数の変域ってなんだろうか。とりあえず教科書をみてみると、
変数のとる値の範囲
のことを「変域」っていうらしい。
ん??
これじゃあイマイチぴんと来ないから、具体的な関数の例をみてみよう。たとえば、
「y = 2x」 という関数があったとする。
この関数での「変数」って「x」と「y」だったよね??
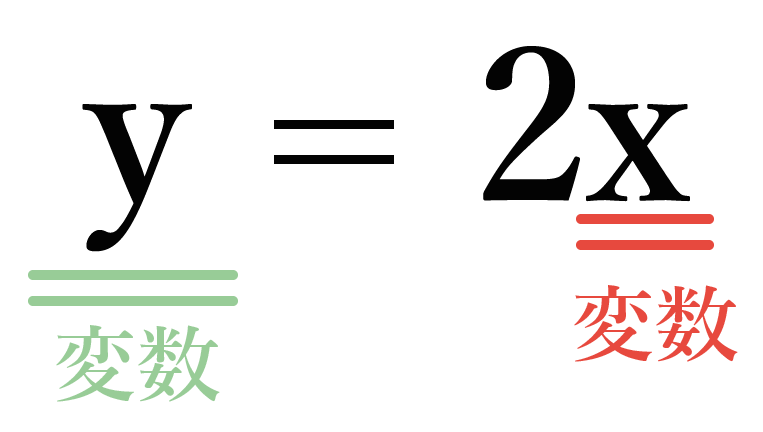
だって、xを変えるとyの値も変わるからね。たとえば、xに「2」をいれたときと、
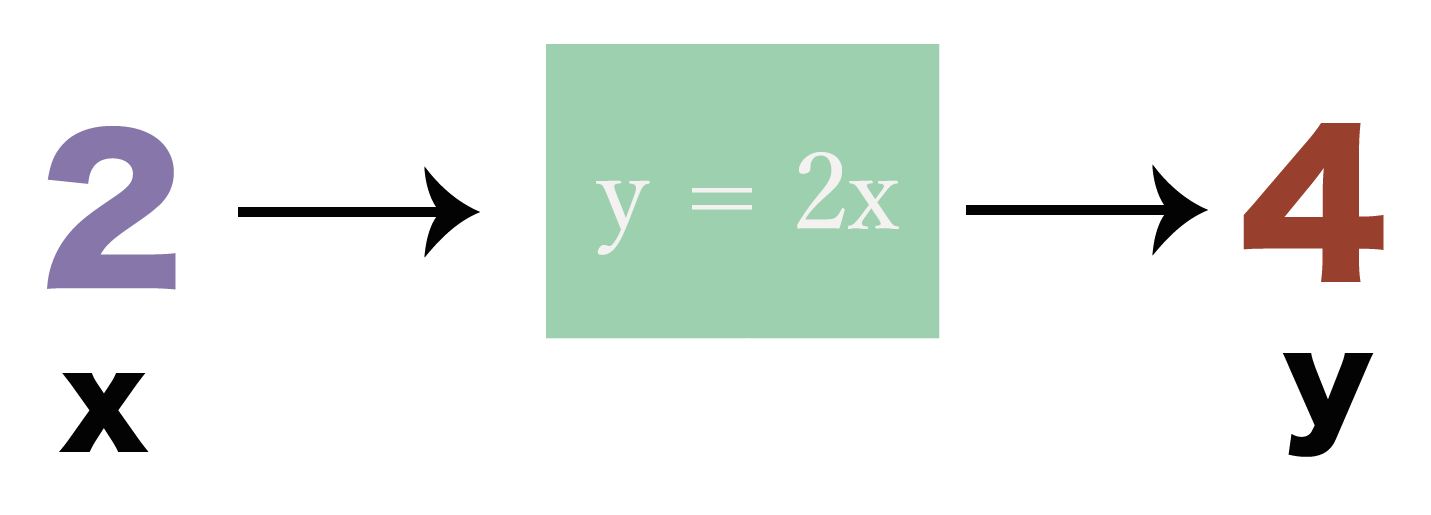
「3」をいれたときじゃyの値は変わってくるでしょ??
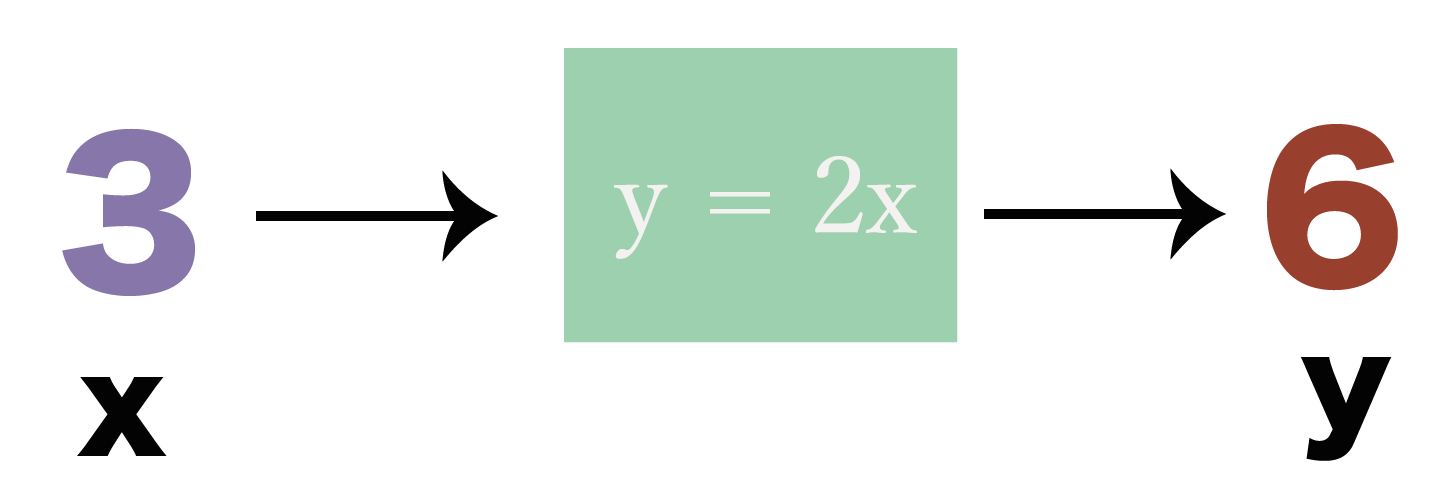
こういう、色んな数を入れたりできる数や、それによって異なる数字がでてくる文字を「変数」って呼んでいたね。
xとyのような変数がとれる「値の範囲」のことを「変域」っていうんだ。
中学数学で登場する「変域」の例
たとえば、
「y=2x」という関数の調子がわるいとしよう。故障中のため、xに入れることができるのは、
0以上2以下の数
っていうことになった。
これが「xの変域」だ。数式であらわすと、
0 ≦ x ≦ 2
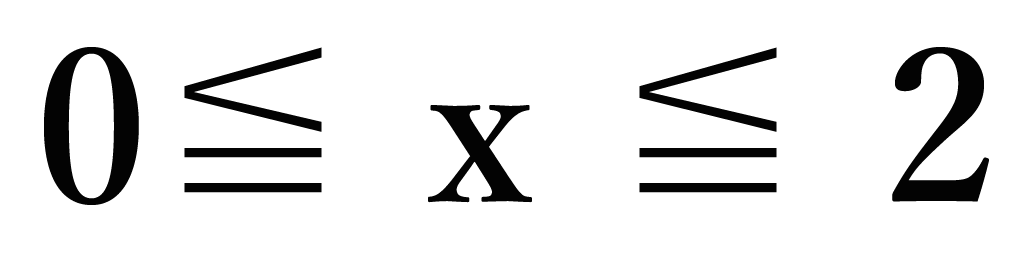
となるね。
このxの変域が「y = 2x」で適用されるとき、
xに2を入れることはできても、
xに3を入れることはできないんだ。
だって、xは「2以下」じゃなきゃダメよ。
っていう変域が設定されているからね。
中1数学で「変域」といえば、
「変数xの範囲のこと」を指す場合が多いよ。
変域がxかyのかで迷ったら「xの変域」ってことにしちゃえばいい。
もっとわかりやすい変域の例(自動販売機??)
関数とはなにか??という記事で、
関数は自動販売機みたいなもんだよ。
って説明したね??
変域の意味を理解するときも「自動販売機のたとえ」をつかってあげると分かりやすいんだ。
たとえばここに、自動販売機があったとする。ちょっと古い。
で、じつは、
500円玉を認識できなくて、しかも一回に1枚のコインしか入らない
という故障をかかえていたとしよう。
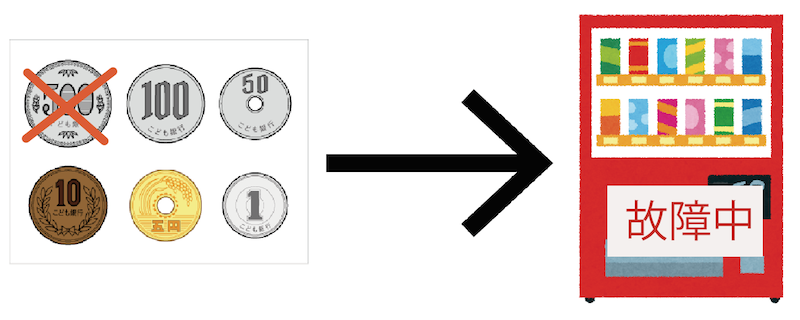
このとき、この自動販売機にいれるお金をxとしたら、xの変域ってなんだと思う??
そう。
0 ≦ x ≦ 100
さ。えっ、なぜなら、
お金を何もいれない状態(x=0)がいちばん小さくて、
100円玉を1枚いれる状態(x=100)がいちばん大きいからさ。500円玉(x=500)は
0 ≦ x ≦ 100(0以上100以下)
という変域の外にでてしまってるね??
だから、500円玉は入れられないんだ。どう??ちょっと変域が身近になったでしょ??
まとめ:変域とは「変数の値の範囲のことである」
関数の変域がちょっとわかったような気がした??
次回はいよいよ「比例」について勉強していくねー!
そんじゃねー。
Ken