【簡単公式】半球の表面積の求め方がわかる2ステップ
半球の表面積の求め方はむずい??
こんにちは!この記事をかいてるKenだよ。そろそろ進撃したいね。
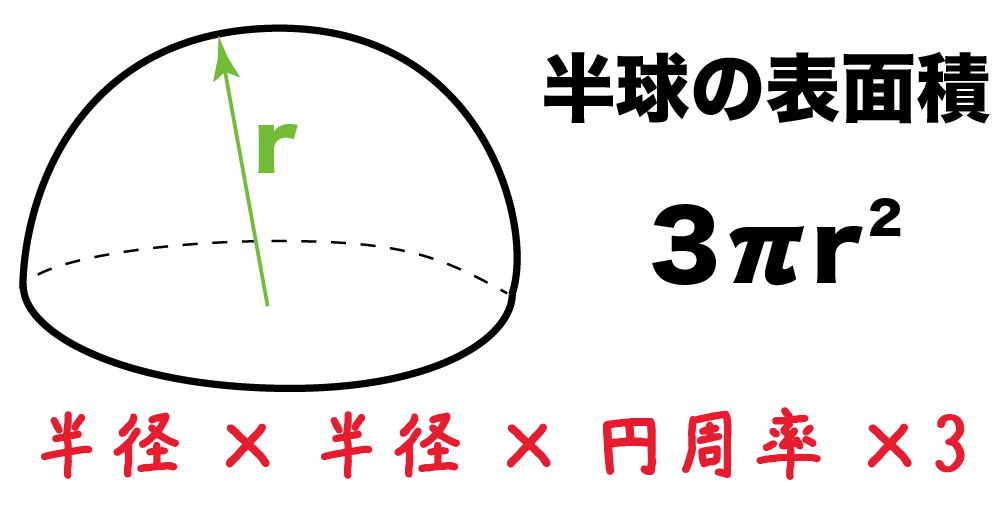
半球の表面積の公式は簡単。
半径をrとすると、
3πr^2
で計算できちゃうんだ。
つまり、
半径×半径×円周率×3
ってわけだね。
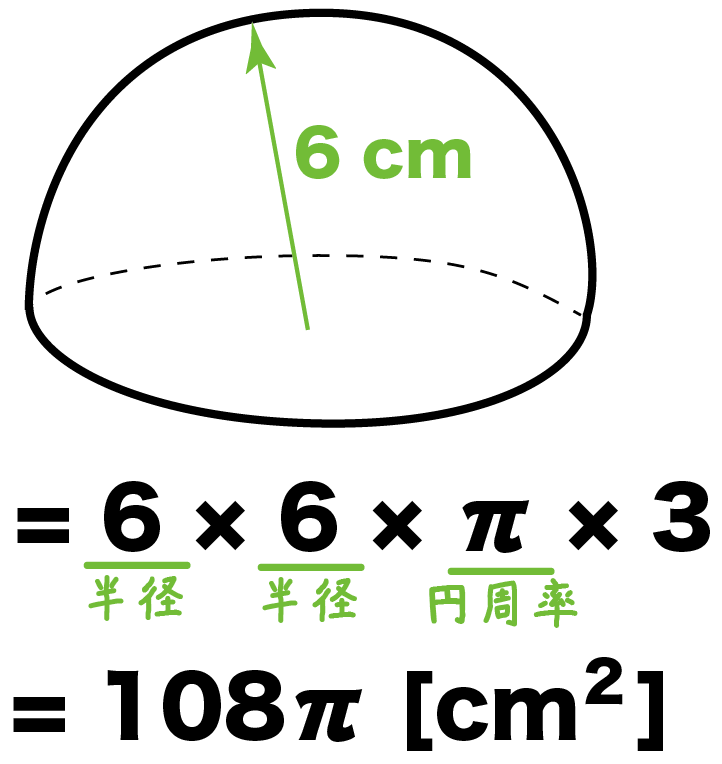
たとえば、半径が6cmの半球があったすると、こいつの表面積は、
半径×半径×円周率×3
= 6 × 6 × π × 3
= 108π [cm^2]
になるんだ。
どう??
半径と円周率かけるだけさ!
どうして半球の表面積が求められるの??
半球の表面積の求め方はわかった。
だけど、
なんで球の表面積の半分じゃないの??
って思うよね。
半球の体積は「球の体積の半分」だったのに・・・ってね。
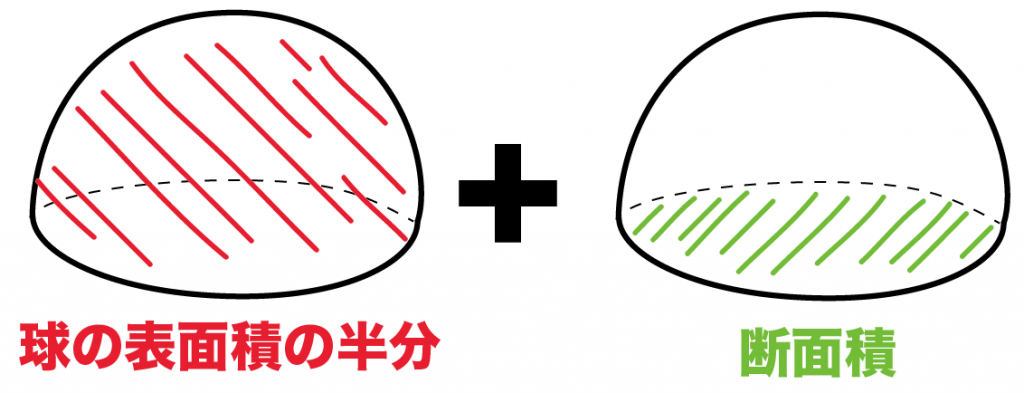
じつは球の表面積は、
- 球の表面積の半分
- 断面積
っていう2つの面積で成り立っているんだ。
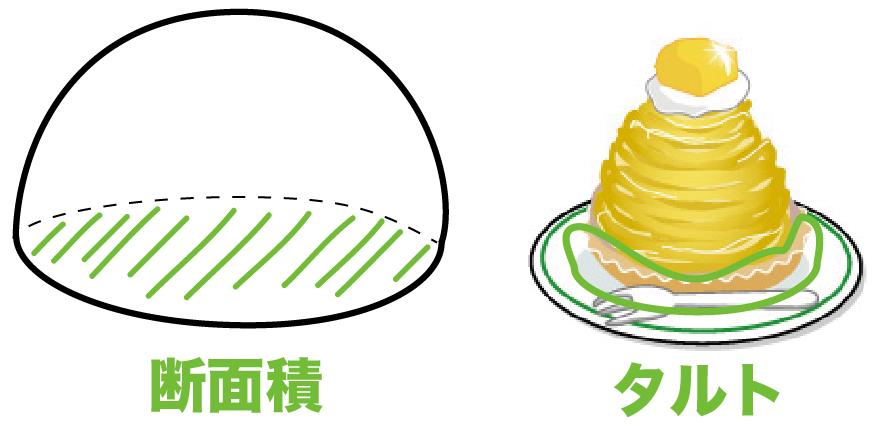
モンブランケーキでいえば、
- クリームの部分
- タルト
って感じ。
こいつらの面積を別々に求めて、最後にたしてるんだ。
試しに、半径6cmの半球の表面積を計算してみよう!!
球の表面積の半分を計算する!
まずは、球の表面積の半分をだそう。
モンブランでいうと、クリームがついている部分だね。
4πrの二乗
だったよね??
ってことはその半分は、
2πrの二乗
になるはず!
だから、半径が6cmの半球のクリーム部は、
半径×半径×円周率×2
= 6×6×π×2
= 72π [cm^2]
になるんだ。
断面積を計算する!
つぎは半球の断面積だ。
つまり、底面の面積をたせばいいよ。
モンブランでいうと「タルト」にあたるね。
半球の断面積は円。
円の面積の公式は、
半径×半径×円周率
だったよね??
だから、例の半径6cmの半球の断面積でいうと、
半径×半径×円周率
= 6×6×π
= 36π [cm^2]
になるね。
たす!
あとは、
- 球の表面積の半分
- 断面積
の2つをたすだけ。
例の半径6cmの半球の表面積は、
(球の表面積の半分)+(断面積)
= 72π + 36π
= 108π [cm^2]
になるんだ。
おめでとう!
これで半球の表面積も計算できちゃうね。
まとめ:半球の表面積は断面積を忘れずに
半球の表面積はトリッキー。
球の表面積の半分じゃないんだ。
球の表面積の半分に、底面積をたすからね。
半球の体積の求め方とはひと味ちがうから注意しよう!
そんじゃねー
Ken