数学の歯車問題（比例の利用）がよくわからん！？
こんにちは！この記事をかいているKenだよ。鼻呼吸は大事だね。
中学数学でよく、
歯車の問題
ってでてくるね。もっとぶっちゃけいうと、
比例・反比例の利用
の問題でよくねらわれるんだ。
なぜだかしらんけど、よく歯車が登場するよ。
たとえば、つぎのような問題だ。
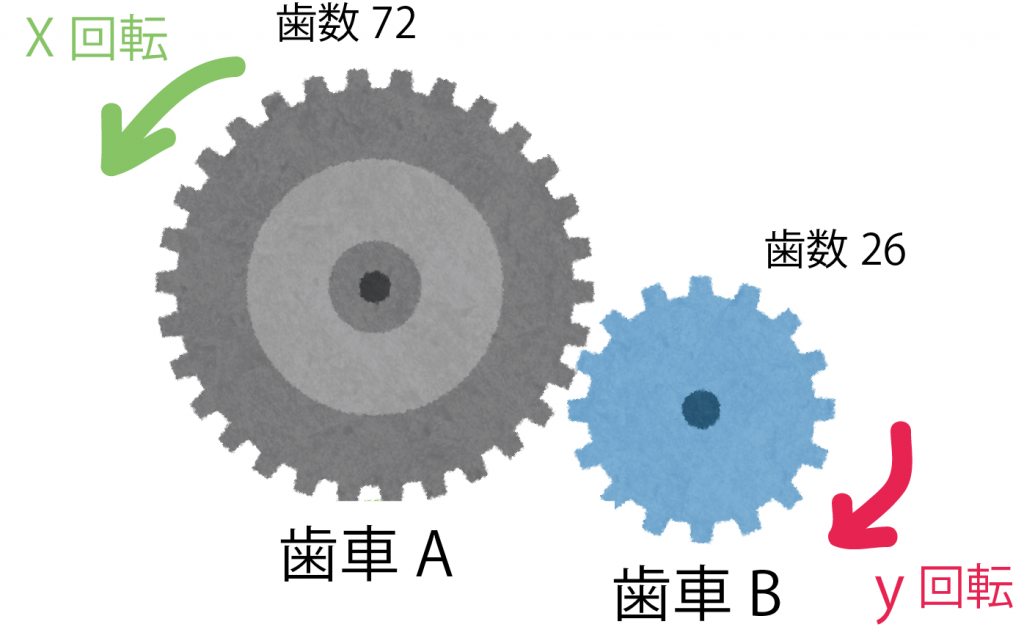
歯数がそれぞれ72、26の歯車A、Bがかみ合っている。歯車Aがx回転する間に歯車Bはy回転する。
yをxの式であらわし、比例しているか、反比例しているか答えなさい。
今日はこんな歯車問題にとまどわないためにも、
数学の歯車問題の解き方を4ステップで解説していくよ。
よかったら参考にしてみてね。
中学数学の歯車問題の解き方がわかる4ステップ
つぎの4ステップでとけちゃうよ。
- 動いた歯数をだす
- 「動いた歯数が等しい」という方程式をたてる
- yについてとく
- xの位置をみる
例題をいっしょにといてみよう！
歯数がそれぞれ72、26の歯車A、Bがかみ合っている。歯車Aがx回転する間に歯車Bはy回転する。
yをxの式であらわし、比例しているか、反比例しているか答えなさい。
Step1. 動いた歯数をだす！
まず歯車の、
動いた歯数
を計算してみよう！
動いた歯数は、
（歯車についてる歯数）×（回転数）
で計算できるよ。
例題の歯車A・Bをみてみよう。
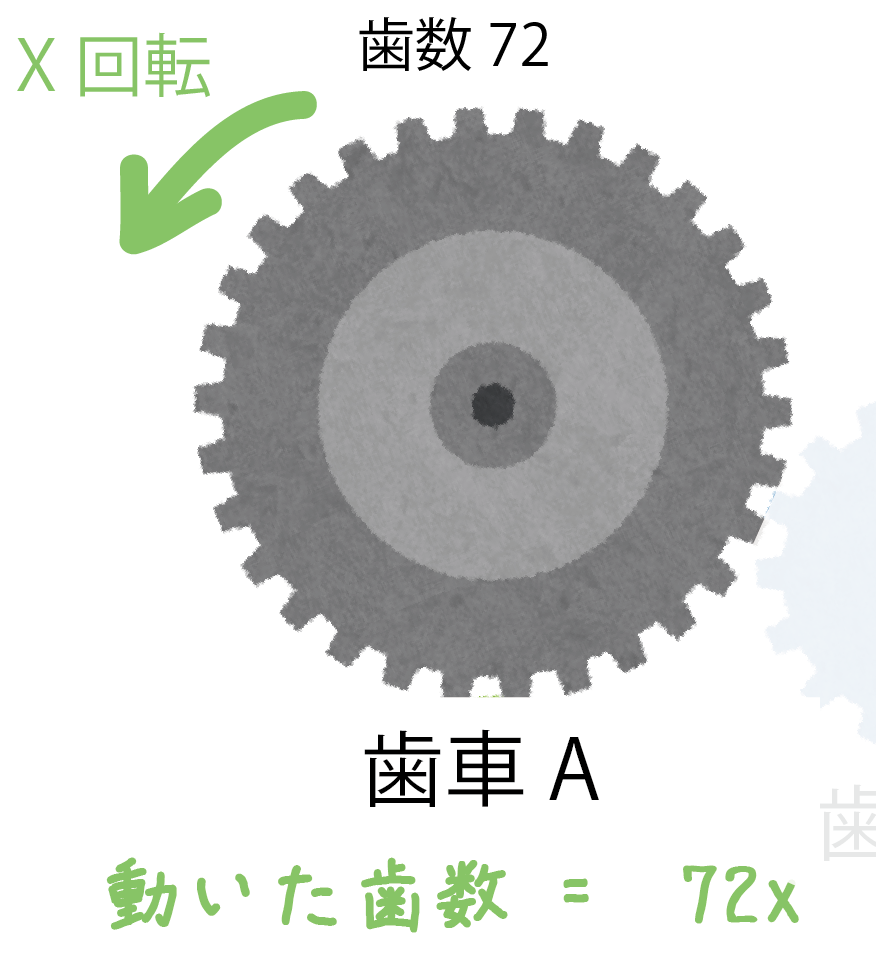
歯車Aは、
- 歯数： 72
- 回転数：x回転
だったね？？
ってことは、歯車Aの「動いた歯数」は、
動いた歯数（歯車A）
= （歯数）×（回転数）
= 72 x
になるね。
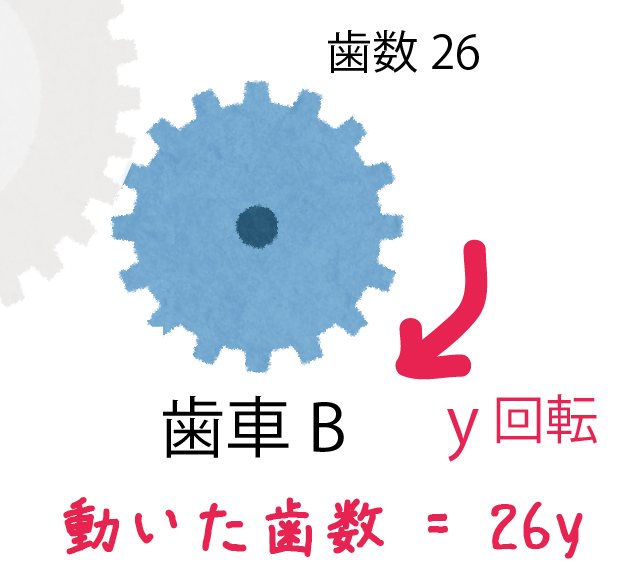
同じように、歯車Bの場合を考えてみて。
歯車Bは、
- 歯数： 26
- 回転数： y
だ。よって、
動いた歯数（歯車B）
＝ 歯数×回転数
= 26y
になる。
これで第1ステップ終了さ！
Step2. かみあってる方程式をつくる
つぎは方程式をつくってみよう！
かみ合っている歯車同士は、
動いた歯数が等しい
っていう性質があるんだ。この性質で方程式をつくってみよう。
例題をみてみると、
歯車A、Bがかみ合っている
ってあるね。
つまり、
歯車A・Bの動いた歯数が等しい
ってことなんだ。
※詳しくは「数学の歯車問題の基礎」を読んでみてね。
だから、
（歯車Aの動いた歯数）＝（歯車Bの動いた歯数）
っていう方程式がつくれるよ。
実際につくってみると、
26x = 72y
になるね。
これが第2ステップ！
Step3. yについてとく
方程式をyについて解いてみよう。
えっ。
「yについて解く」の意味がわからんだって？？！
そうだね。
yを左に持ってきて、xを右にどかして、yを裸にすればいいんだ。
例題でつくった方程式の、
72x = 26y
に注目してみよう。
yについて解いてみると、
72x = 26y
y = 72÷26 x
y = 13分の36x
になるね。
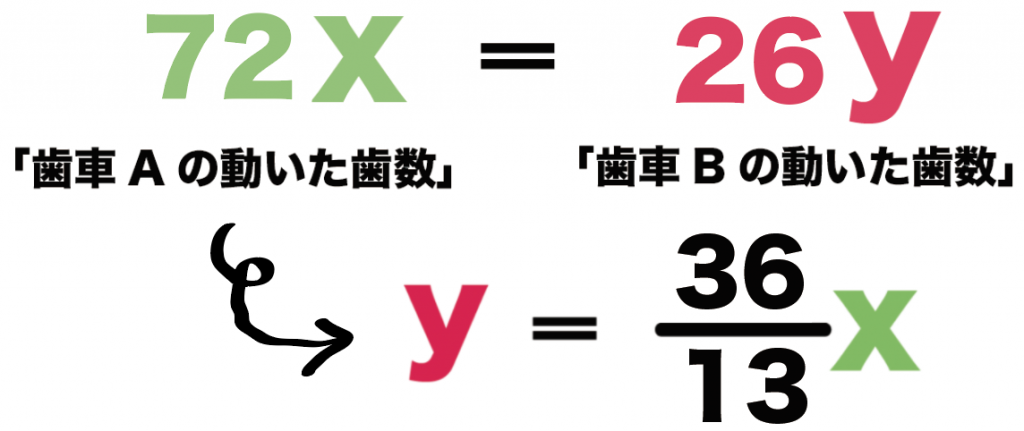
yをxの式であらわせたね。
あとすこし！
Step4. xをさがせ！
最後に、xの位置を確認しよう。
xが、
分子にあるか、
それとも、
分母にあるか
で比例か反比例かが決まってくるんだ。
- xが分子にある ⇒ 比例
- xが分母にある ⇒ 反比例
っていう感じになるよ。
例題の式では、
xが分子の位置にあるよね？？
ってことは、
この方程式は「比例」ってことになる。
どう？？ 納得したかな？？
まとめ： 中学数学の歯車問題も4ステップで攻略！！
数学で歯車の問題がでちゃった？？？
むずそうだって？？
いや、そんなことない。
と
4ステップで攻略さ。
ガンガン歯車問題をといていこう！
そんじゃねー
Ken
