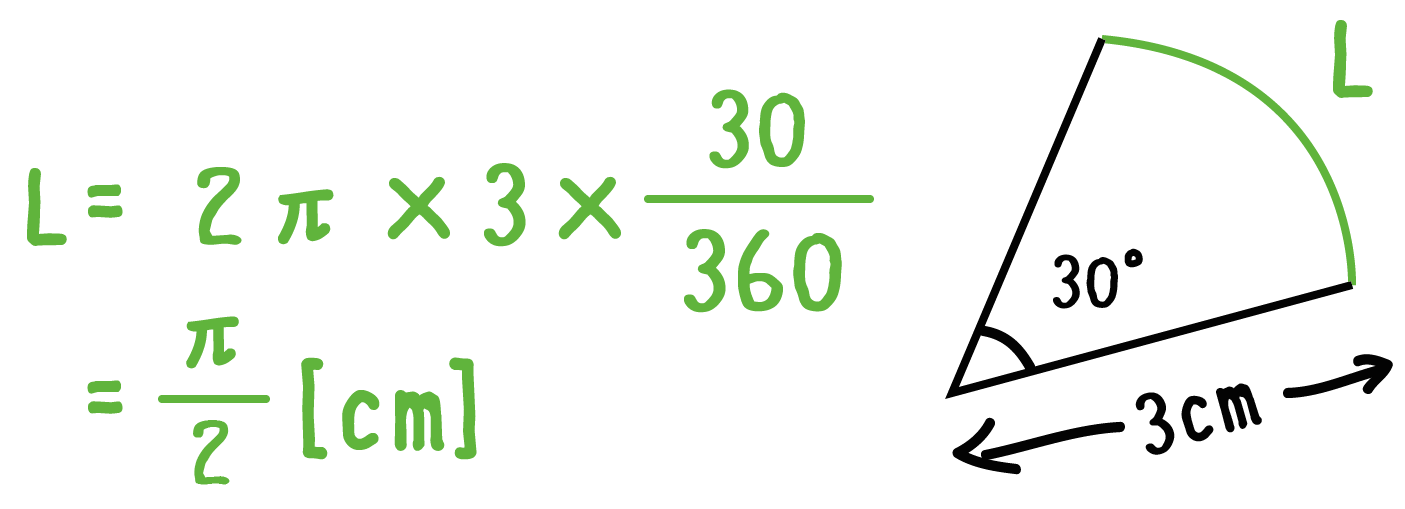2分でわかる!扇形(おうぎ形)の弧の長さの求め方
扇形の「弧の長さの求め方」がよくわからない!??
こんにちは、この記事をかいてるKenだよー!パンケーキはハチミツで食べるのがうまいね。
「扇形の弧の長さ」を求める公式ってわすれやすくない??
テストでたまーに狙われる分野だから、できれば公式をおぼえておきたいね。

今日は、テストで出されたときのために、
「扇形の弧の長さの求め方」の公式を振り返ってみよう!
~もくじ~
- 扇形の弧の長さを求めるためには「ピザ」が必要??
- たった2分で覚えられる扇形の公式
扇形の弧の長さの求め方は「ピザ」で解決??
扇形の弧の長さを求めたい・・・・
そんなときにはどうすればいいのか。
電卓を使う?
ドラえもんに頼る??
ミュージックステーションをみる?
ノンノン。
ノン。
ちょっといい線までいってるけど、そのどれもが間違っている。
じつは、
扇形の弧の長さを求めるためには「ピザ」を思い浮かべるだけでいいんだ。

みんな大好き「ピザ」
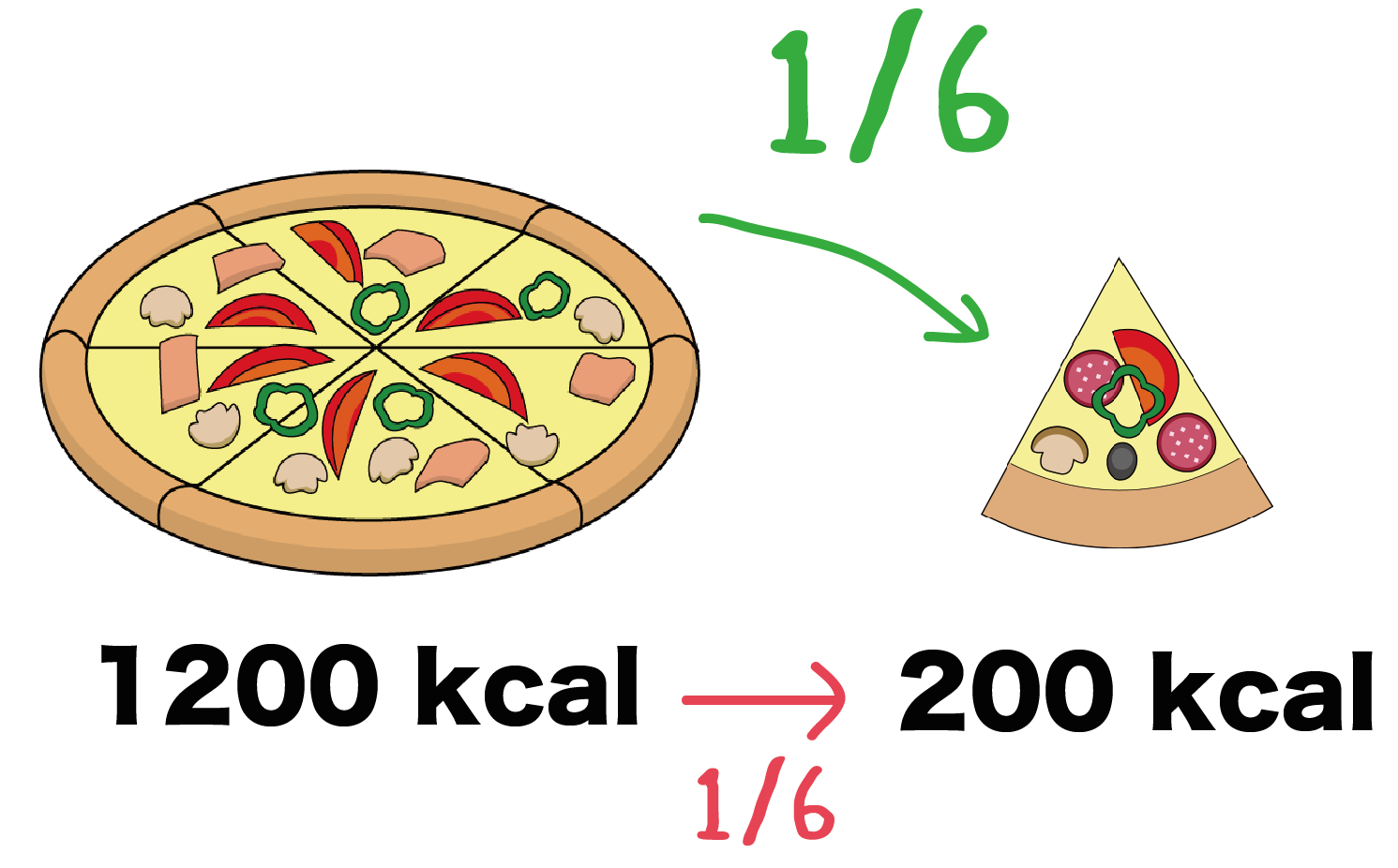
ピザのカロリーを思い出して欲しい。
もし、1200kcalのホールピザを6等分すると、ひとつのピースには200kcalがふくまれているはずだ。
これはどうやって計算したのかというと、
「1つのピース」が「1枚のピザ」から何等分されているのか?
ということをヒントにして求めたんだ。
つまり、ピザの大きさを6等分すると含まれるカロリーまで6等分されるということさ。
これを「扇形の弧の長さ」に応用してあげよう。
扇形が「円の○○分の1」になっているという比を「円周の長さ」にかけてあげるんだ。
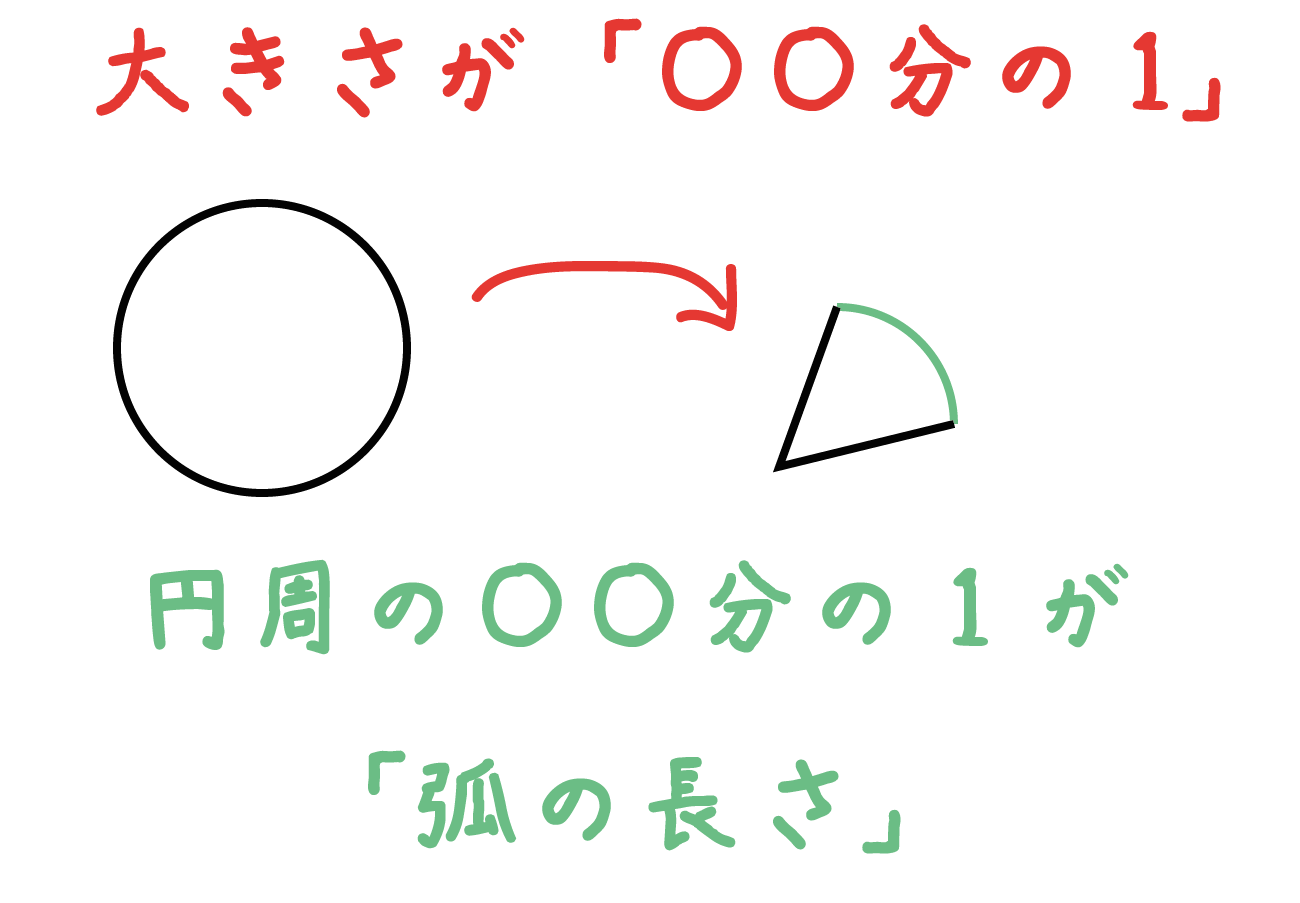
そうすれば、ピザでカロリーを計算したように、「円周」から「扇形の弧の長さ」を求めることができる。
2分でわかる!扇形の弧の長さを求める公式
「扇形の弧の長さ」の求め方の基本はわかったね??
それじゃあ、扇形の弧の長さの公式をみていこう!
扇形の半径をr、中心角をα、円周率をπとすると、
2πr×α/360
で「扇形の弧の長さ」を求められるんだ。 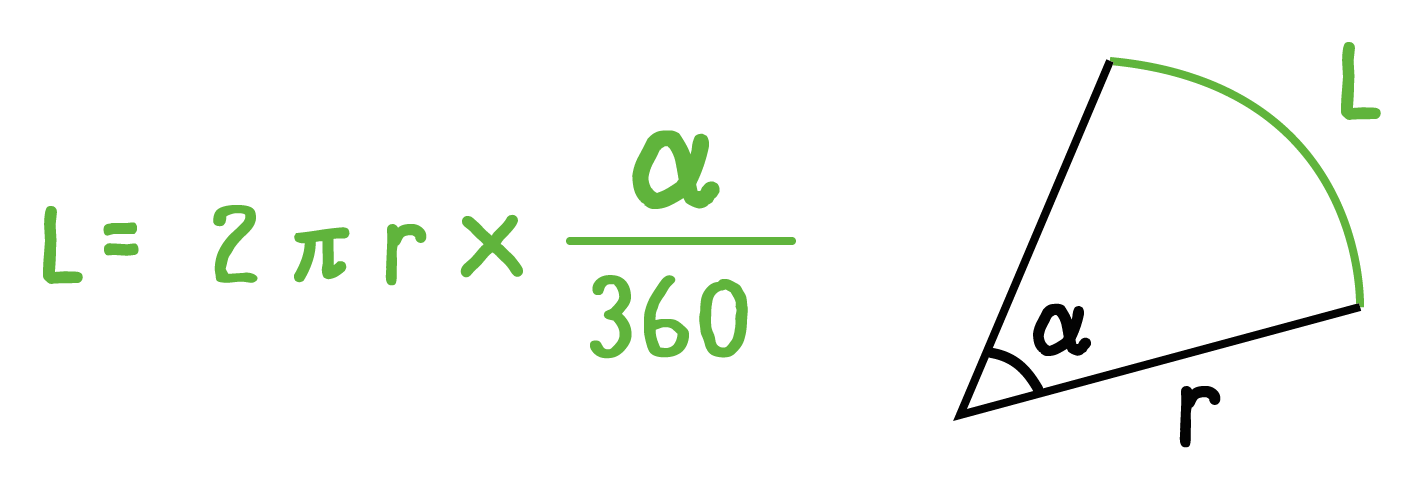
公式のうしろにある「α/ 360」という数値が「扇形が円の○○分の1になっている」ってことをあらわしているよ。
つまり、「円」という1枚のピザを何等分に切ったか??ということがわかる。
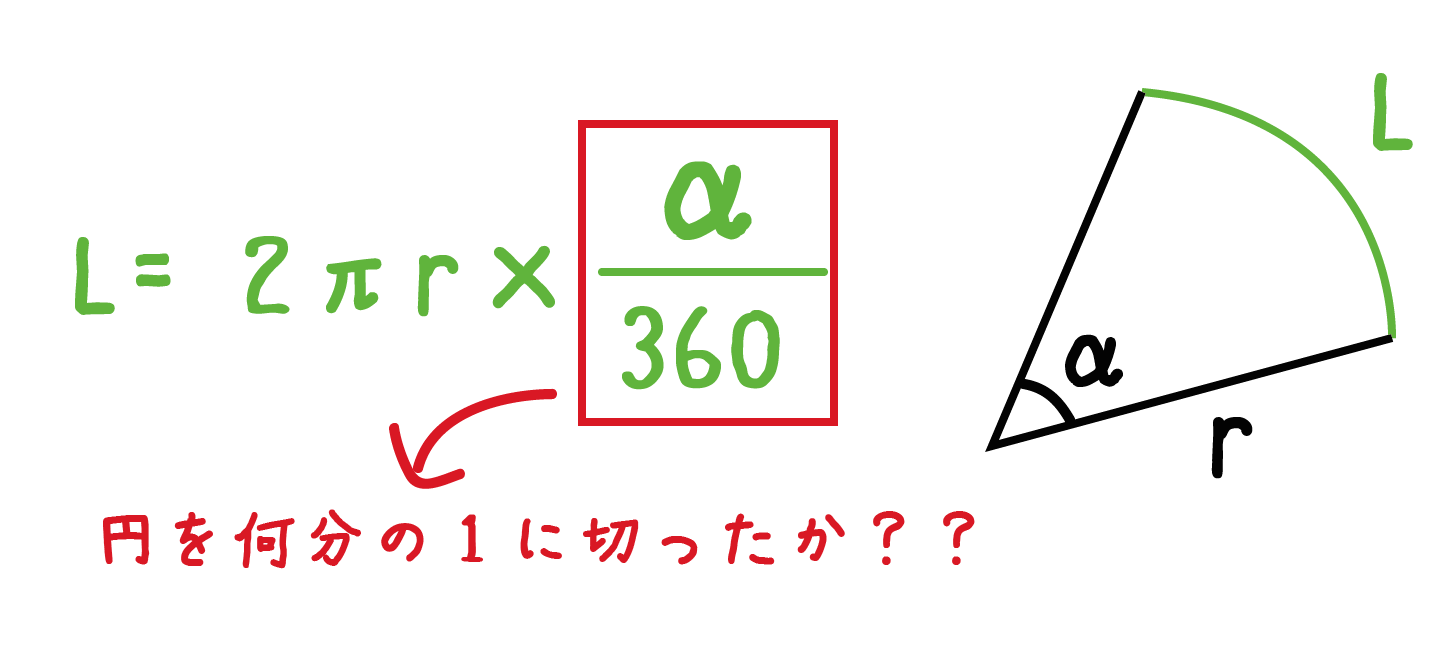
だから、こいつを円周の長さ「2πr」にかけてやると、「扇形の弧の長さ」を計算できるってことになるね。
たとえば、
半径3cm、中心角が30°の扇形がここにいたとしよう。
このとき、扇形の弧の長さLは、
L = 2π × 3 × 30/360
= π/ 2
になるよ。
こんな感じで「扇形の弧の長さ」をバンバン求めていこう!
まとめ:扇形の弧の長さの求め方、おっけい!
さいごに復習しておこう。
扇形の弧の長さLの求め方は、
L = 2πr×α/360
だったね??
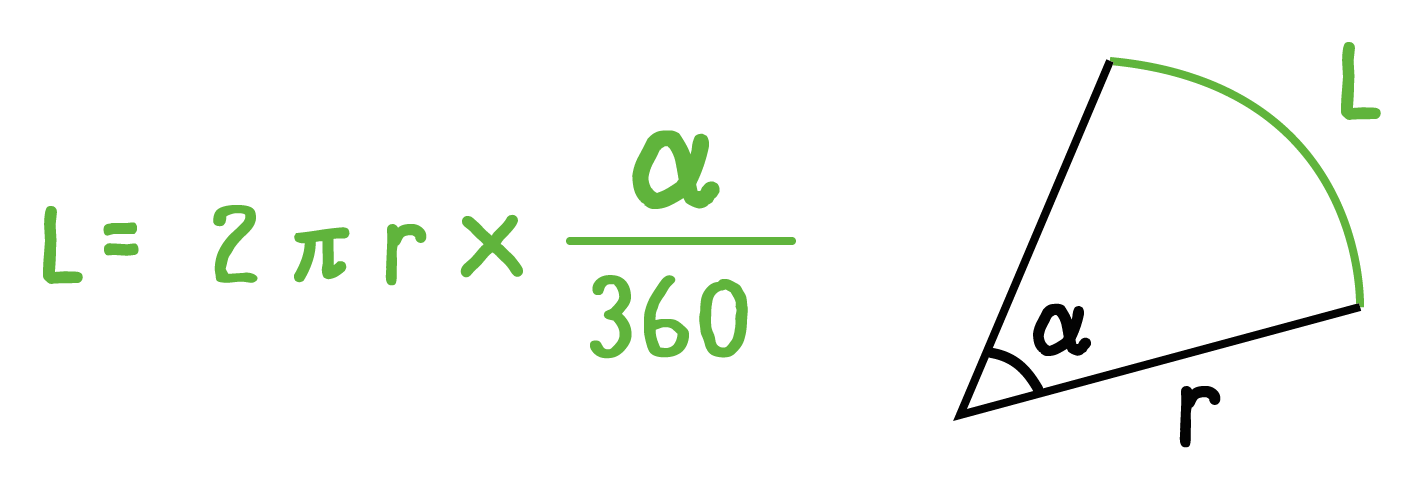
ピザのカロリーを計算するように、扇形の弧の長さを求められれば大丈夫。
時間があったら、扇形の面積の求め方も復習してみてね。
そんじゃねー
Ken