円柱を2つ重ねた立体の表面積の求め方
円柱を2つ重ねた立体の表面積だと・・・?
立体の問題ではこんな問題もあるっぽいよ。
次の立体の表面積を求めよ。
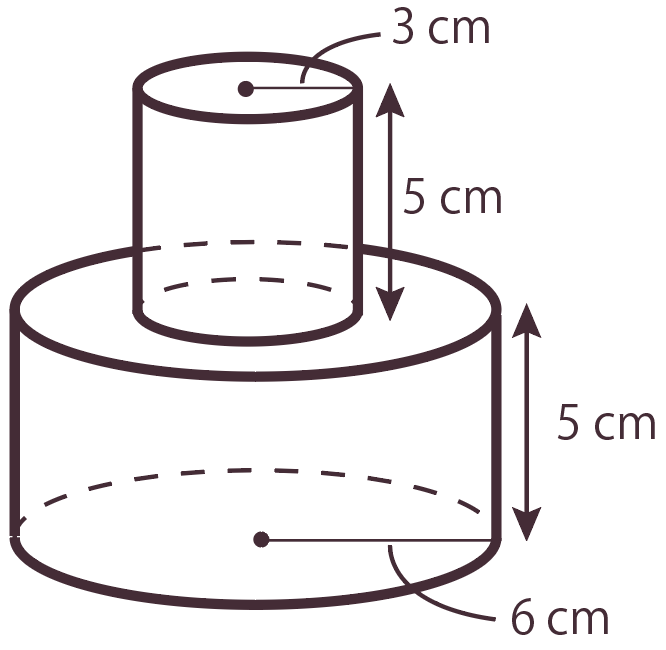
なんと、
円柱を2つ重ねた立体
の登場だ。
しかも「表面積」を求めろ、と。
今まで口を酸っぱく、
表面積を求める前に展開図をかこう
と言ってきたけど、この問題はちょっと例外。
なぜなら、展開図をかくのがむずいからね。
展開図はスルーしよう。
その代わり、
「底面積」と「側面積」を別々に計算して最後に足す
っていう解き方がおすすめ。
底面積を計算
まず底面積を求めよう。
底面は、
- 小さい円柱の上面
- 大きい円柱の上面
- 大きい円柱の下面
の3つだね。
こいつらの面積を計算して最後に足せばいいんだ。
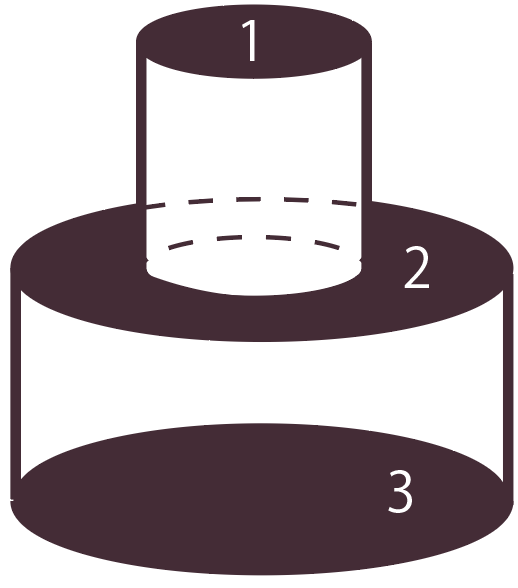
まず、小さい円柱の上面の底面積(上図1)。
半径3 cmの円だから、円の面積公式「半径×半径×円周率」で計算すると、
$$3×3×π$$
$$= 9π[cm^2]$$
だ。

次は真ん中のドーナッツのような図形(上図2)。
大きい円(半径6cm)から、小さい円(半径3 cm)の面積を引けばいいね。
(大きい円の面積) – (小さい円の面積)で計算すると、
$$ (6×6×π)- (3×3×π)$$
$$= 27π[cm^2]$$
になるね。
最後は下に敷かれているでかい円の面積。
こいつは半径6cmの円だから「半径×半径×円周率」で面積を計算すると、
$$6×6×π$$
$$= 36π[cm^2]$$
になる。
これらの底面積をぜーんぶ足してやると、
$$9π + 27π + 36π$$
$$= 72π[cm^2]$$
になるね。
側面積を求める
次は側面積を求めよう。
「上の円柱の側面(1)」と「下の円柱の側面(2)」の面積を足せばいいんだ。
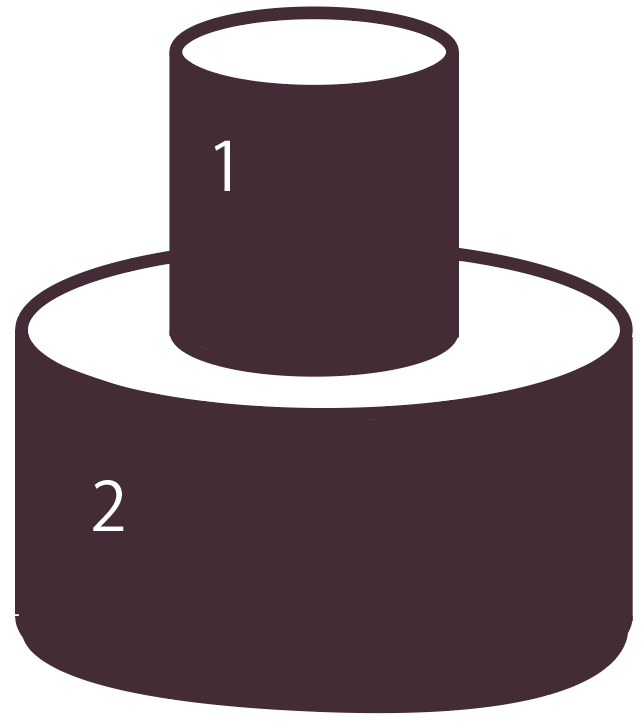
ここで円柱の側面積の求め方の復習ね。
直径×高さ×円周率
で計算できたよね?
上下の円柱の側面積を「(小さい円柱の表面積)+(大きい円柱の表面積)」で足すと、
$$(6π × 5)+ (12π × 5)$$
$$= 30π + 60π$$
$$= 90π[cm^2]$$
になる。
底面積と側面積を足す
あとは底面積と側面積を足すだけ。
「底面積+側面積」を計算すると、
$$72π + 90π$$
$$= 162π [ cm² ]$$
になるはず。
こんな感じで、円柱が2つくっついていようが、基本は変わらない。
表面積を求めるために、底面積と側面積を足すのさ。
そんじゃねー
Ken



