円錐にかけたひもの最短距離を求める3ステップ
円錐にかけたひもの最短距離を知りたい??
こんにちは!この記事をかいているKenだよ。バターチキン最高。
円錐にひもをかける問題ってあるよね???
たとえば、つぎのような問題だ。
例題
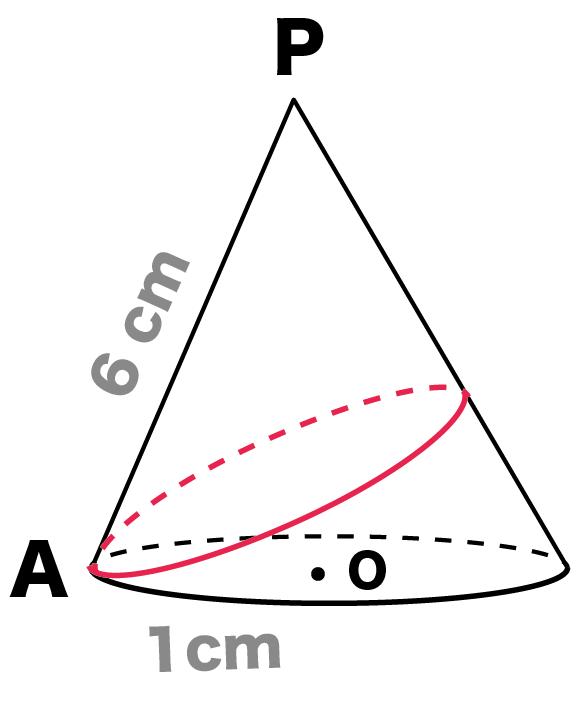
母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。
なんで円錐にひも???
って思うかもしれないね。
正直、とくのがつらい。
だけど、
円錐にかけたひもの最短距離を求める問題
ってよくでてくるんだ。
今日はこのタイプの問題の、
円錐にかけたひもの最短距離を求める問題の解き方
を3ステップで解説してみたよ。
よかったら参考にしてみてね。
円錐にかけたひもの最短距離を求める3ステップ
3ステップでとけちゃうよ。
- 展開図をかく
- 中心角をだす
- 直角三角形の比をつかう
例題をといていこう。
例題
母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。
Step1. 展開図をかく
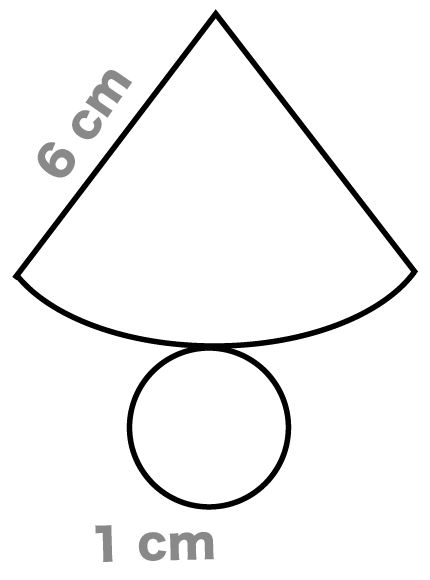
円錐の展開図をかいてみよう。
とりあえず、円錐の展開図っぽいやつをかこう。
中心角は気にしなくていいよ。
これが第1ステップさ。
Step2. 側面の中心角をだす
つぎは側面の「扇形の中心角」をだしてみよう。
出し方は簡単。
中心角をxとして方程式をたてればいいんだ。
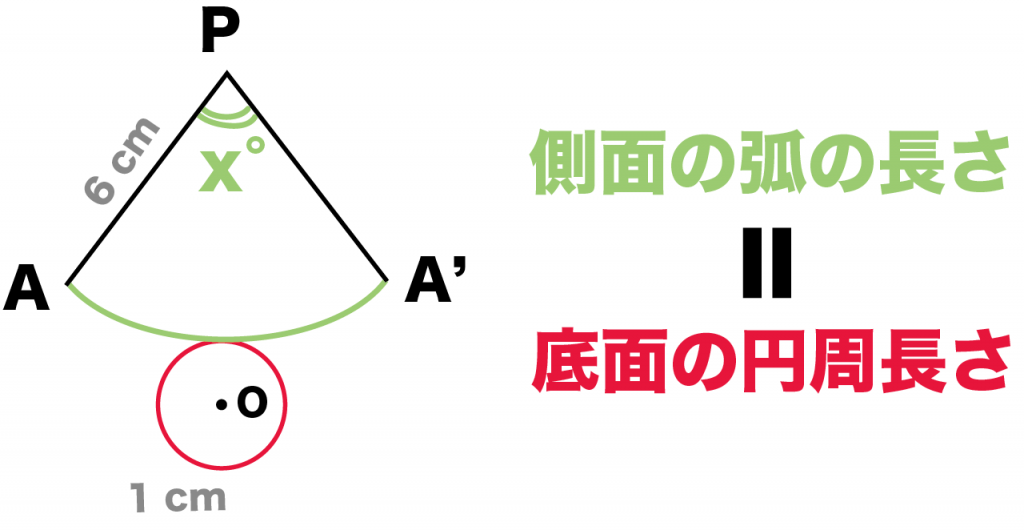
側面の扇形の弧の長さ
と
底面の円周の長さ
が等しい
っていう式をつくればOK。
例題をみてみよう。
中心角をxとしたから、
- 扇形の弧の長さ: 2×6 ×π× X ÷ 360
- 底面の円周長さ: 2× 1 × π
になるね。
だから方程式は、
(扇形の弧の長さ)=(底面の円周長さ)
2×6 ×π× X ÷ 360 = 2× 1 × π
になる。
これをといてやると、
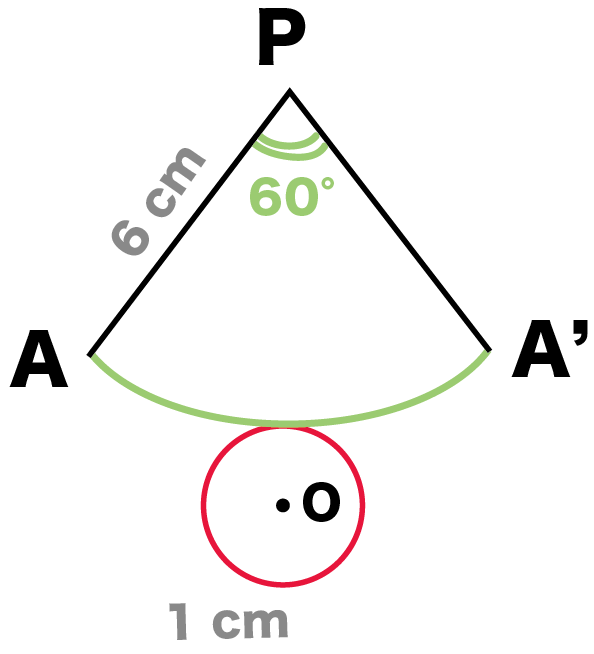
中心角X = 60°
になるはずだ。
Step3. ひもをかく
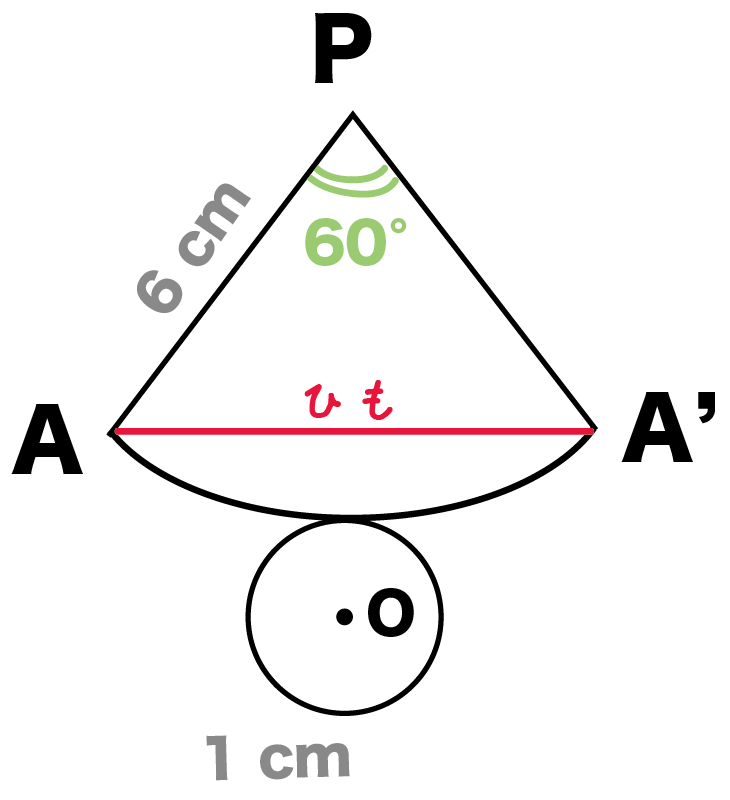
つぎは展開図に「ひも」をかいてみよう。
例題でいうと、赤いひもは、
AからスタートしてAにもどってきているよね??
しかも、その長さが最短距離。
ってことは、展開図でいうと、
A
と
組み立てたらAに重なるA’
を直線でむすんでやればいいんだ。
Step4. 直角三角形の比をつかう
最後は直角三角形の比をつかおう。
「ひも」と「母線」でできた三角形に注目してくれ。
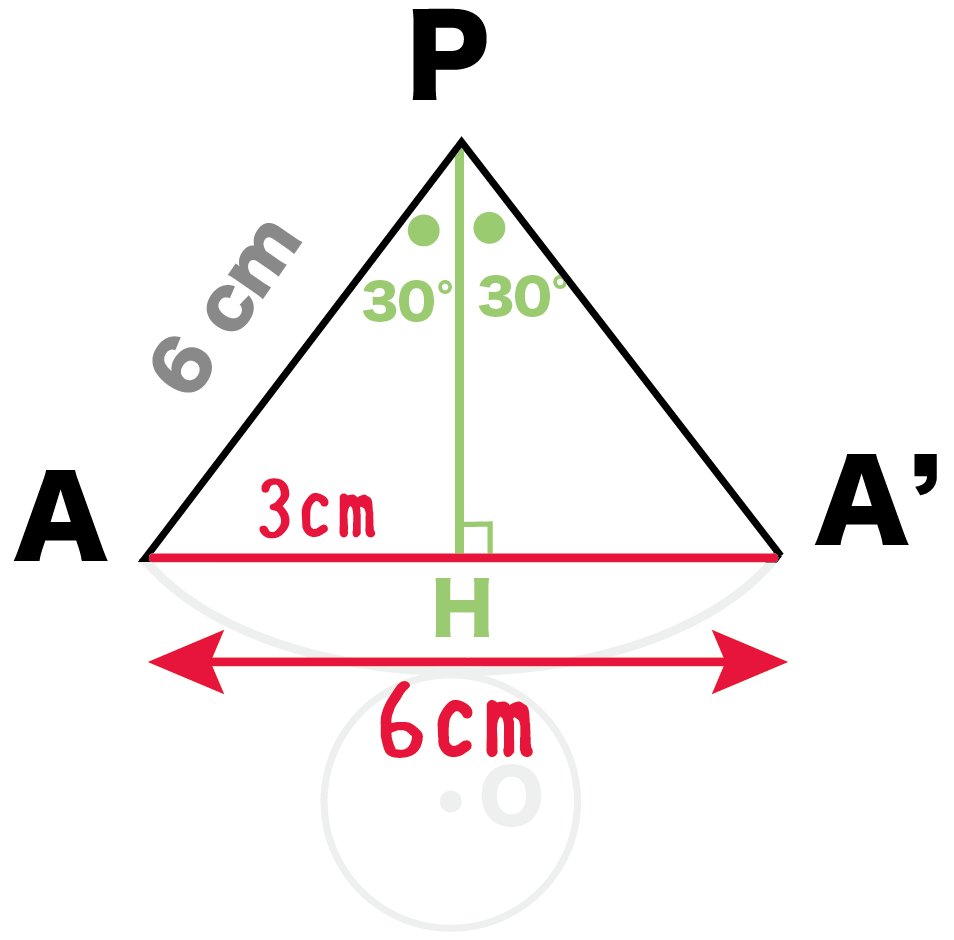
例題でいうと、△PAA’だね。
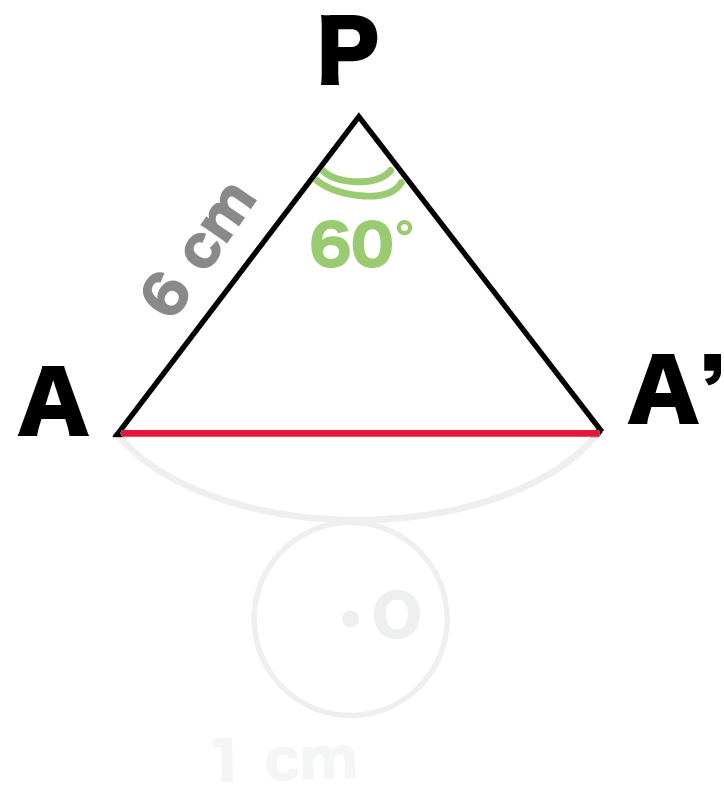
こいつは、
- 頂角P = 60°
- PA = PA’ = 6 cm
の二等辺三角形。
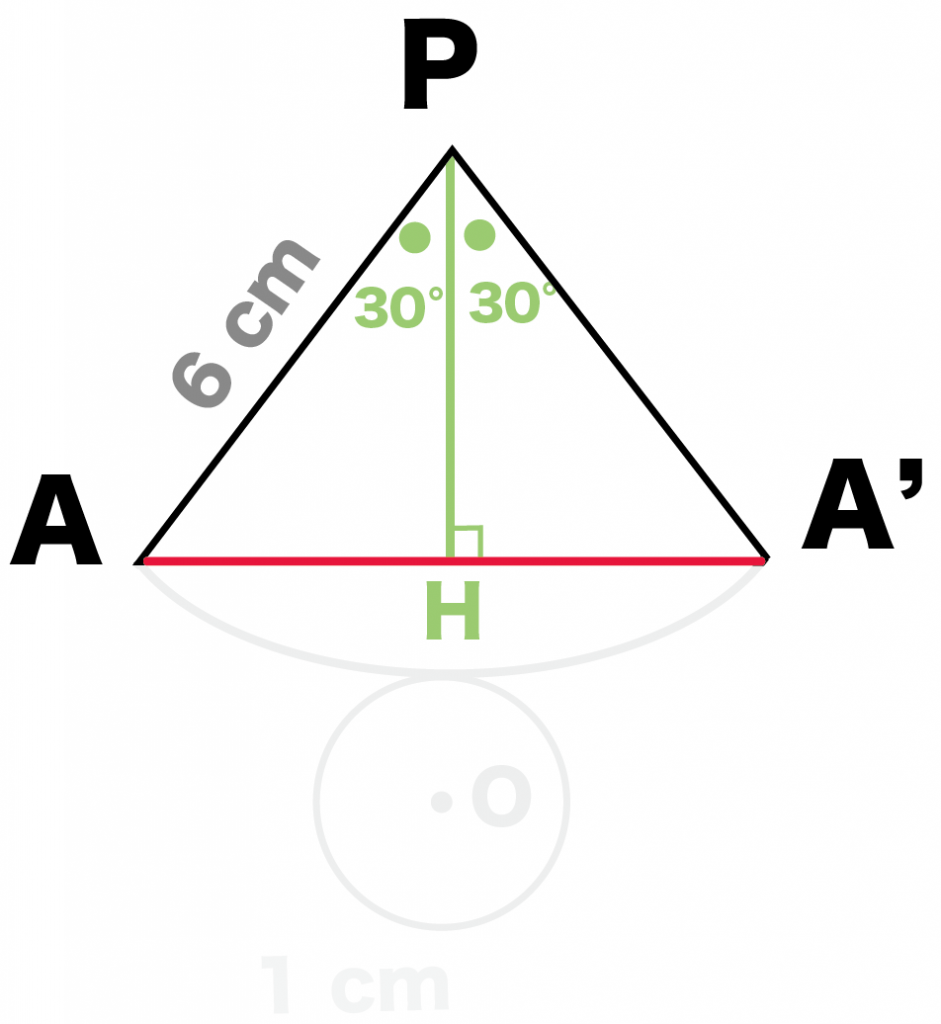
頂角の二等分線は底辺を垂直に二等分する
というやつを使ってみよう。
PからAA’に二等分線をひく。
交点をHとすると、
- 角AHP = 90°
- 角APH = 30°
になるね。
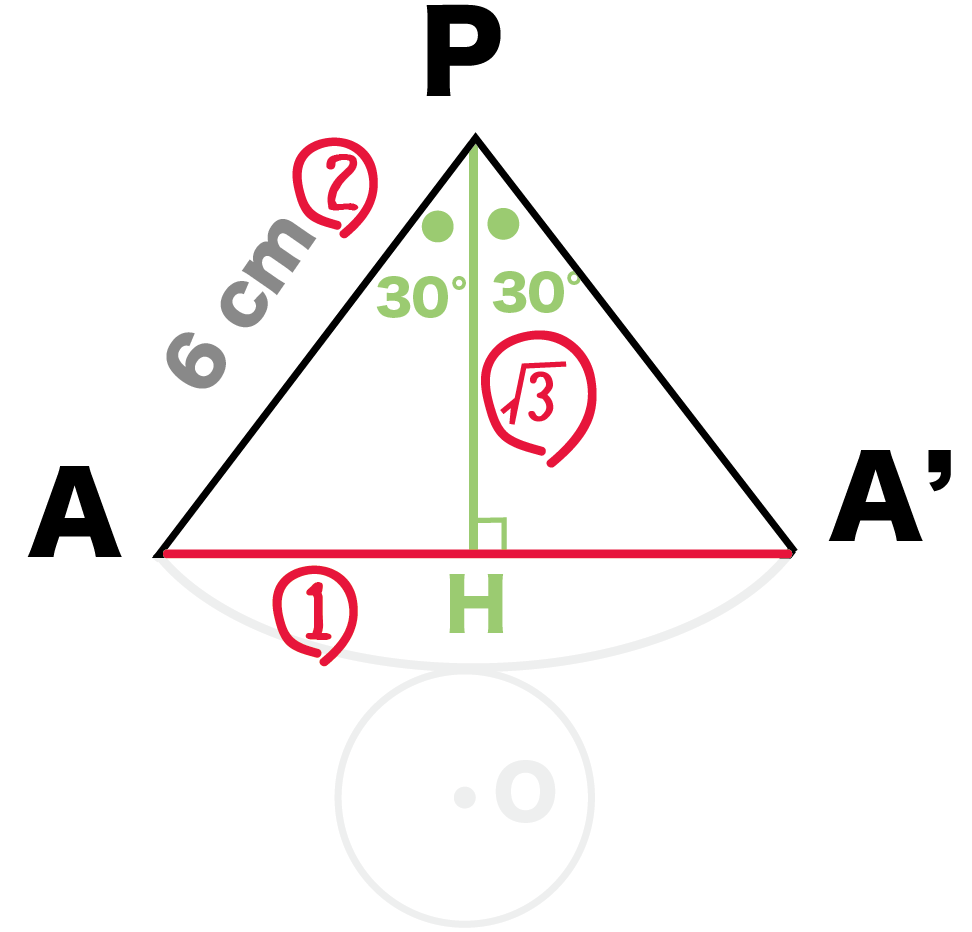
んで、
△APHは頂角30°の直角三角形だから、
1 : 2: √3
の辺の比になっているはず。
よって、
AP: AH = 2: 1
AH = 3 cm
になる。
PHはAA’の垂直二等分線になっているはず。
よって、
ひもの長さAA’
= 2 × AH = 6 cm
になるね。
おめでとう!
これで、ひもでも糸でもなんでもこいだね!
まとめ:円錐にかけたひもの最短距離は超総合問題!
最短距離の問題って、
- 扇形の中心角の求め方
- 円錐の展開図の作図
- 直角三角形の比
の知識が必要になってくる。
ってことはつまり、
1~3年生の知識をフル活用しないと解けない。
だから入試問題にでやすいのかもね。
テスト前によーく復習しておこう。
そんじゃねー
Ken