こんにちは!この記事をかいているKenだよ。健康はマジ大事だね。
ルートでやっかいなのは、
平方根の分数の計算だ。
なぜなら、
平方根を簡単にしたり、
分母を有理化したりで忙しいからね。
ルートの分数の計算なんて解きたくないぜ。
今日はそんなちょっとやっかいな、
ルート分数の割り算の計算方法
を4ステップで解説していくよ。
よかったら参考にしてみて。
ルート分数の割り算は4ステップだ。
例題をといてみよう。
例題
つぎのルート分数の割り算をしなさい。
5分の√20 ÷ √(15分の2)
まずは、割り算を掛け算になおそう。
ルート分数の割り算なのに、はやくも÷にバイバイ。
寂しいけどね、仕方ないんだ。
割り算を掛け算になおす方法は1つ。
それは、
「÷」を「×」にして分母と分子を入れ替えるのさ。
例題でもおなじ。
まず、「÷」を「×」にしちゃって、
「÷」のうしろの「√(15分の2)」の分子と分母をいれかえる。
すると、
5分の√20 ÷ √(15分の2)
= 5分の√20 × √(2分の15)
になるね。
つぎは約分だ。
分母と分子に公約数があったら約分しよう。
例題の計算式をよくみて。
5分の√20 × √(2分の15)
「5分の√20」の分子の「√20」、「√(2分の15)」の分母の「√2」に公約数があるね。
そう、√2だ。
ってことは、こいつらを√2でわれるから、
5分の√20 × √(2分の15)
= 5分の√10 × √(1分の15)
になる。
分母・分子どうしで掛け算しよう。
ルートの掛け算の仕方をつかってみてね。
例題でも、分母・分子それぞれ計算すると、
5分の√20 × √(2分の15)
= 5分の√10 × √(1分の15)
= 5分の√150
になる。
最後に、ルートを簡単にしてやろう。
いちばん最初にルートを簡単にしたほうがいいだろ??
って思うかもしれない。
だけどね、分数の割り算の場合はそうじゃない。
なぜなら、
ルートの中身をガッツリ約分できる可能性あるからね。
簡単にするのは約分まで待ったほうがいいんだ。
例題では分子の「√150」を簡単にできそうだね。
なぜなら、
150のなかには「5の2乗」がふくまれてるからさ。
ってことは、5をルートの外にだせる。
すると、
5分の√150
= 5分の5√10
= √10
になるね。
おめでとう!
ルート分数の割り算もマスターだ。
平方根の分数の割り算はどうだったかな??
ほかのルート計算とたいして変わらないね。
ちょっと違うのは、
ルートを簡単にするのをステイする
ってことだ。
ガッツリ約分してから簡単にしても遅くない。
じっくり分数の割り算をしていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。野菜摂取したいね。
ルート計算でヤッカイなのは、
分数がまじった問題
だ。
シンプルな平方根の計算ならいけるんだけど、
分数がからむとヤッカイだ。
そこで今日は、
ルート分数の掛け算の計算方法
を3ステップで解説するよ。
よかったら参考にしてみて。
例題をといていこう。
例題
つぎの平方根の計算をしなさい。
5分の9√2 × √3分の1
ルート分数の掛け算は3ステップでとけちゃうよ。
分母を有理化しよう。
答えは有理化しなきゃいけないから、先にやっちまうのがベストだ。
⇒ 分母の有理化の方法はこちら
例題では「√3分の1」の分母にルートがあるね??
こいつを有理化しちゃおうぜ。
分母から√3を消し去るために、分母・分子に√3をかけてみて。
すると、
5分の9√2 × √3分の1
= 5分の9√2 × 3分の√3
になるね。
もし、分母・分子に公約数があるなら約分すればいい。
例題でいうと、
が約分できそうだ。
なぜなら、
「9」と「3」の公約数は3だからね。
こいつらを約分してみると、
5分の9√2 × 3分の√3
= 5分の3√2 × 1分の√3
になるね!
分母・分子を掛け算しよう。
ルートの掛け算では、中身を掛け算しちゃえばよかったね??
⇒ルートの掛け算の仕方はこちら
例題でも計算してみると、
5分の9√2 × 3分の√3
= 5分の3√2 × 1分の√3
= 5分の3√6
になるね。
おめでとう!
ルート分数の掛け算もバッチコイだ。
最後に、計算問題をといてみて。
練習問題
つぎの平方根をふくむ計算をしなさい。
⇒練習問題の解答はこちら
どう??うまくとけたかな?!
問題をといて掛け算に慣れていこう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。どら焼きは脳にきくね。
ルートの計算には色々ある。
なかでも、いちばんむずいのは、
ルート(平方根)の分数の計算
だ。
ただでさえ、ルートの計算で精一杯。
なのに、そ、それを分数にしちゃうんだもん!?
クソやっかいだね。
今日は、ルート分数の計算をマスターするために、
平方根の分数の足し算・引き算の計算の仕方
を5ステップで解説していくよ。
さっそく計算方法を紹介していくよ。
5ステップで分数の足し算・引き算ができちゃうんだ。
例題をといてみよう。
つぎの平方根の分数の計算をしなさい。
3分の√12 + √27分の6
ルートを簡単にしよう。
ルートの中身から、2乗の因数をとりだせばいいのさ。
⇒ くわしくは「ルートを簡単にする方法」を読んでみてね。
例題の計算式では、
を簡単にできそう。
なぜなら、
ルートの中に2乗の因数がふくまれてるからね。
√12だったら、2の2乗、
√27だったら3の2乗が入ってる。
それぞれ簡単にすると、
3分の√12 + √27分の6
= 3分の2√3 + 3√3分の6
になるね。
これが第1ステップ!
つぎは、分母の有理化だ。
分母からルート(無理数)をなくせばいいんだ。
⇒ くわしくは「分母の有理化」をよんでみて。
例題をみると、
2つめの項の分母に「√3」があるね。
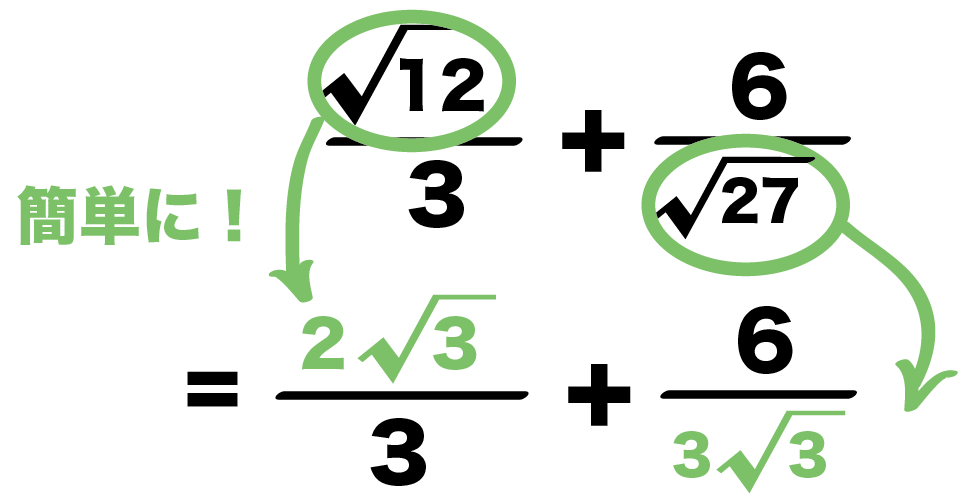
このルートをなくすために、
分母と分子に「√3」をかけるんだ。
すると、例題のルート計算式は、
3分の√12 + √27分の6
= 3分の2√3 + 3√3分の6
= 3分の2√3 + 9分の6√3
になる!
つぎは、通分しよう。
通分ってようは、
分数たちの分母をそろえる
ってことさ。
例題の分数たちはそれぞれ、
だったよね??
これじゃあ分母が「3」と「9」でバラバラだ。
分母を最小公倍数の9にあわしてやると、
になるね!
つぎは分子を足し算・引き算しちゃおう。
例題でも分子を足し算してやると、
3分の√12 + √27分の6
= 9分の6√3 + 9分の6√3
= 9分の12√3
になるね。
最後は、ルートの分数を約分してみよう。
約分してすっきりしたほうがいいじゃん?
例題でも計算結果の、
9分の12√3
を約分しよう。
分母の「9」と分子の「12」の共通の約数に3がある。
ってことは、3で約分できるはずだから、
9分の12√3
= 3分の4√3
になるね。
これでルートの分数の計算は終了だ!
平方根の分数の足し算・引き算はどうだったかな?
5ステップもあってむずそうだけど、使っているのはどれも過去のワザ。
スムーズにとけるように踏ん張ってみよう。
最後に練習問題を用意したから、よかったら解いてみてね。
練習問題
つぎの平方根の計算をしなさい。
√3分の4 – √2分の1 + 6分の√2
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。ウェイトは重いね。
平方根の問題はたくさん、ある。
ルートの計算問題とか、
平方根の大小をくらべる問題とか、ルートの近似値を求める問題とかね。
もう、ほんと多種多様すぎるぜ。
そんななか、基本で忘れちゃならないのが、
ルート(根号)をはずす問題
だ。
これは文字通り、
平方根を「√」を使わないで表す問題だね。
今日はこの、
ルート(根号)の外し方
を解説していくよ。
2ステップで外せちゃうんだ。
つぎの練習問題をといてみよう。
つぎの数字たちをルートを使わないで表現してみてください。

まずルートの中身をいじくろう。
中身の数字を、
2乗のカタチ
にすればいいんだ。
たとえば、
とかね。
とりあえず、なんでもいいから2乗になってればいいわけだ。
例題の平方根たちを「2乗のカタチ」にすると、
になるね。

つぎは簡単。
ルート
と
指数の2
を消しちまえばいいのさ。
たとえば、
√a²
っていう平方根をイメージしてみて。
そったら、
「√」と「2乗」をとってやって、
a
にすればいいんだ。
例題の平方根は、
こんなかんじで「2乗のカタチ」になったね??

あとは、こいつらから「√」と「2乗」をとりのぞくだけ。
すると、
になるね!
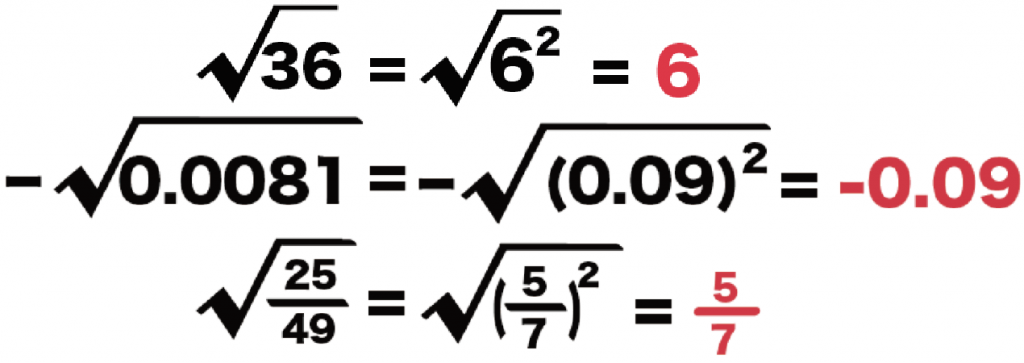
これでルートをうまくはずせたね。
ルートのはずし方は簡単。
根号の中身を2乗のカタチにして、
「√」と「2乗」をとっぱらえばいいんだ。
ルートの外し方は基本中の基本。
テスト前にしっかりマスターしておこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。時差に要注意だね。
ルートの計算で間違いやすいのは、
足し算・引き算
だ。
よくあるミスで、
ルートの中身を足し算・引き算しちゃう
ってやつがある。
たとえば、
√2 + √3
だったら、中身の2と3をたして、
√2 + √3
=√5
みたいな感じでね。
だけどね、この平方根の足し算の仕方は、
とんでもなく間違っているんだ。
ほんとうに。
とんでもなくね。
なにがっあってもダメ。
地球が反転しても、磁力がおかしくなっても、ダメ。
√の中身はゼッタイに足し算・引き算しちゃいけないんだ。
まじで、ムリ。
平方根の近似値で計算してみればきづくはずだ。
√2と√3の近似値はそれぞれ、
だったよね??
計算すると、
√2 + √3
≒ 1.414 + 1.732
≒ 3.146
になるね!
3.146っていう数字はあきらかに√5の近似値じゃない。
だって、√5の近似値は、
2.2360679(富士山麓オームなく)
だったもんね??
足し算・引き算では中身がおなじ平方根の整数だけ計算しよう。
たとえば、
√a +√a
= 2√a
みたいな感じでね。
計算の仕方は文字式の足し算・引き算に似てる。
文字式の計算でも、おなじ文字しか足し引きしちゃいけないよね??
それと同じさ。
でもさ、
なんでルートの中身を足し算・引き算しちゃいけないのかな??
雰囲気的にはいけそうな気がするもん。
今日はせっかくだから、
なぜ平方根の中身を足し算、引き算しちゃいけないのか
をみていこう。
まずは、
√a + √b
を2乗してみよう。とりあえずね。
展開の公式で計算すると、
( √a + √b )^2
= (√a)^2 + 2√ab + (√b)^2
= a + 2√ab + b
になるね!
さっき生み出した等式の、
( √a + √b )^2 = a + 2√ab + b
両辺に√をつけてみよう。
なぜ、ルートをつけるのかというと、
( √a + √b )^2
から2乗をとっぱらいたいからだ。
さっそく、左と右にルートをつけてやると、
√{( √a + √b )^2} = √(a + 2√ab + b)
になるね!
左辺の中身は(√a+√b)の2乗になってるから、
√と2乗をそのまま消せる。
すると、
√a + √b = √(a + 2√ab + b)
になるね。
このことからわかるのは、
√a + √b = √(a + b)
にならないってことだ。
余計な「2√ab」が入ってるのさ。
ルートの足し算・引き算で気をつけるべきこと。
それは、
ルートの中身をたしひきしちゃいけない
ってことだ。
文字式の足し算・引き算とおなじ計算方法
っておぼえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。出会いは突然だね。
ここまで、
を勉強してきたね。
こいつらはぶっちゃけ簡単。
ルートの中身を掛け算・割り算すればいいからね。
でもじつは、平方根の計算でめんどいのは、
ルートの足し算・引き算
なんだ。
足し算・引き算をマスターすれば大丈夫。
どんな平方根の計算もクリアできるはずさ。
今日はその、
平方根(ルート)の足し算・引き算の計算方法
を解説していくよ。
よかったら参考にしてみてね。
足し算・引き算は3ステップで計算できるよ。
例題をといてみよう。
例題
つぎの平方根の計算をしなさい。
√18 – √75 +√32
ルートを簡単にしよう。
簡単にすると計算しやすくなるからね。
⇒ ルートを簡単にする方法はこちら
例題では、
の3つの項を簡単にすると、
になる。
だから、例題の計算式は、
√18 – √75 +√32
= 3√2 – 5√3 + 4√2
になるね。
ルートの中身がおなじ項をさがしてみて。
たとえば、
みたいにね。
例題でもルートの中身を確認してみると、
の2つの平方根の中身がいっしょ!
ルートの中身が2だ。
中身がおなじ平方根の「整数部分」を足し算・引き算しよう。
ルートの中身は足し算・引き算しないでね。
例題で中身がおなじ平方根は、
の2つだね??
整数部分を足し算・引き算すると、
√18 – √75 +√32
= 3√2 – 5√3 + 4√2
= 7√2 – 5√3
になる。
これでルートの足し算・引き算は終了!
中身がちがう「-5√3」は放置していいんだ。
ルートの足し算・引き算の仕方はどうだった?!?
計算のコツはただ1つ。
中身が同じ項の整数部分だけ計算すればいい
だ。
文字式の計算に似てるね。
問題をガンガンといてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。湿度はほどほどね。
ルートの計算にはいろいろある。
足し算、引き算、掛け算・・・って感じでさ。
もうね、ありすぎて疲れちまうよ。
今日はルート計算をマスターするために、
ルート(平方根)の割り算の仕方
を勉強していこう。
= もくじ =
ルートの割り算には基本ルールがある。
それは、
分子・分母のルートをいっしょにしてもいい
ってやつだ。
たとえば、√a、√bがあったとすると、
√b 分の √a = √(b分のa)
になる。
えっ。これが割り算と関係があるのかッテ??!
そうだね。
割り算は分数であらわせたよね。
a÷b
なら
b分のa
って感じで。
÷のうしろの数を分母に、それ以外を分子にもってきてるわけ。
これをルートの割り算でもつかうと、
√a÷√b = √b分の√a
になるんだ。
んで、これにさっきのルールでつかうと、
√a÷√b = √b分の√a = √(b分のa)
になる。
そして、途中の真ん中をはぶくと、
√a÷√b =√(b分のa)
になるね。
つまり、
√をいっしょにして、÷の後ろを分母にしてもいいんだ。
これがルート割り算の基本ルールだ。
ルートの割り算は5ステップでいけるよ。
例題をいっしょにといてみよう。
例題
つぎのルートの割り算を計算してください。
√24 ÷ √10
ルートを簡単にしよう。
ルートの中身から2乗の因数を外にだせばいいんだ。
⇒ ルートを簡単にする方法はコチラ
例題では、
ルート24
が簡単にできそうだね??
なぜなら、素因数分解すると、
24 = 2の3乗 × 3
になるからね。
ルートの外に「2の2乗」をとりだせそうだ。
√24を簡単にすると、
√24 ÷√10
= 2√6 ÷ √10
になるね!
割り算を分数にしよう。
やり方は簡単。
「÷の後ろの数」を分母にもってくればいいのさ。
√a÷√bなら、
√b分の√a
ってかんじにできる。
例題の割り算では、
√10
が÷の後ろにきてるね??
だから、こいつを分母にもってくると、
√24 ÷ √10
= 2√6 ÷ √10
=√10分の2√6
になるよ。
分数を1つにまとめよう。
√b 分の √a = √(b分のa)
っていう基本ルールをつかえばいいのさ。
例題でもおなじ。
√10分の√6
のルートをいっしょにしてあげると、
√24 ÷ √10
=√10分の2√6
= 2×√(10分の6)
になるね!
ルートの中身を約分しよう!
スッキリしていいじゃん!?
例題のルート内の分数は、
10分の6
だね??
こいつを約分すると、
5分の3
になる。
だから、さっきの計算式は、
√24 ÷ √10
= 2×√(10分の6)
= 2×√(5分の3)
になるんだ。
最後に、分母を有理化しよう。
分母の平方根を分子と分母にかければいいのさ。
⇒くわしくは「分母の有理化のやり方」を読んでみてね。
例題の分母は√5。
だから、分子と分母に√5をかけると、
√24 ÷ √10
= 2×√(5分の3)
= 5分の2√15
になるね。
おめでとう!
これでルートの割り算マスターだ。
平方根の割り算の仕方はどう??
5ステップあるからなげえかもしれない。
だけど、どのステップも基本的なこと。
ルートの割り算に必要なものをしっかり
とおさえてこう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。腹は八分だね。
平方根の計算でたまに、
ルートの分数
がでてくる。
分子や分母にルートがまじってるわけだ。
なかでもヤッカイなのは、
分母に平方根(ルート)がまじってる問題
だ。
なぜなら、
分数の分母の有理化
っていう作業が必要だからさ。ふつうより手間かかるんだ。
今日はそんな計算をクリアするために、
分数の分母の有理化のやり方
をわかりやすく解説していくよ。
よかったら参考にしてみて。
= もくじ =
分母の有理化とは、
分母のルート(無理数)を有理数にしちゃう
ってことなんだ。
もっといえば、
分母のルートをとっぱらうこと
だ。
いかなる手をつかってもいい。
分母の無理数を有理数に変えられればokだ。
分母の有理化は簡単。たったの3ステップだよ。
練習問題をといていこう!
例題
つぎの分数の分母を有理化しなさい。
√24 分の3
ルートを簡単にするとこからはじめよう。
ルートを簡単にするって、
ルートの中身から2乗の因数を取り出す
だったよね??
⇒くわしくは「ルートを簡単にする方法」をみてね。
例題の「√24 分の3」の「√24」に注目してほしい。
この平方根は簡単にできる。
なぜなら、
24には因数「2の2乗」がはいってるからね。
えっ。疑わしいって??
24を素因数分解すると、
24 = 2の3乗×3
になるよね??
このなかに「2の2乗」っていう因数がふくまれるぜ。
こいつを根号の外にだすと、
ルート24分の3
= 2ルート6分の3
になるんだ。
これが第1ステップ!!
分母の平方根を分子と分母にかけよう。
これによって、
分母の平方根が2乗されてルートがとれるんだ。
たとえば、「√a分のb」って分数がいたとしよう。
分母・分子に√aをかければいいのさ。
すると、
√a分のb
= (√a×√a)分の(b×√a)
= a分の(b√a)
になるね!
例題の分数の分母は、
2√6
だったよね??
分母の「ルート6」を分母と分子にかければいいんだ。
すると、
ルート24分の3
= 2ルート6分の3
= 12 分の3√6
になるね!
最後に約分しよう。
約分しなくても間違いじゃないけど念のためね。
例題でも約分してみよう。
12分の3√6
分子と分母を3でわると、
4分の√6
になるね!
おめでとう!
これで分母の有理化もマスターだ。
分数の分母にルートがある??
そんなときは、分母を有理化してやろう。
平方根を簡単にして、
分母のルートを分子と分母にかければいいのさ。
ゆっくり有理化になれていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。海につかりたいね。
平方根の計算にはいろいろある。
それこそ、
足し算、引き算、割り算、、、、、とか、もう、数えきれない。
そんななかに、
ルートの掛け算の計算
がある。
ルートの中身を掛け算するだけ
だったよね??
そんなむずくなさそう。
だけどね、実際の計算問題だとそうはいかない。
そんなに世間は甘くないんだ。
そこで今日は、平方根の掛け算の計算方法を紹介していくよ。
平方根の掛け算は5ステップで計算できるよ。
えっ。5ステップもあるからダルいって!??
ノンノン。
複雑にみえるけど、一瞬で計算できる。
安心してくれ。
例題をといていこう。
例題
つぎの平方根の計算をしてください。
(1) √12 × √32 (2) √7 × √21 (3) √48 × √27
平方根を簡単にしてみよう。
「ルートを簡単にする」ってようは、
2乗になってる因数を取り出す
ってことだ。
⇒ くわしくは「平方根を簡単にする方法」をよんでみて
例として、(1)をみてみよう。
(1) √12 × √32
√12と√32をそれぞれ簡単にしてやると、
になる。
つぎは(2)の掛け算だ。
(2) √7 × √21
この平方根たちは簡単にできないね。
なぜなら、中身に2乗の因数がないからさ。
(3)も簡単にしてやると、
(3) √48 × √27
= 4√3 × 3√3
になるね!
つぎは、整数の掛け算をしよう。
ルートはいったん無視していいや。
例題の(1)の計算でいうと、
(1) √12 × √32
= 2√3 × 4√2
だったよね??
だから、整数の掛け算は、
2×4
= 8
になるね。
おなじように、(3)でも計算すると、
4×3
= 12
になるね!
ちなみに、(2)は整数がないからステイね。
つぎは、平方根の掛け算をするよ。
ルートを1つにして中身だけ計算しちゃう
だったよね??
例題でもおなじさ。
(1) √12 × √32
= 2√3 × 4√2
の平方根部分の掛け算は、
√3 × √2
= √6
になるね!
例の(2)もおなじ。
平方根の掛け算の基本をつかって計算すると、
√7×√21
= √147
になるね!
例題の(3)の、
√48 × √27
= 4√3 × 3√3
でもおなじさ。
平方根の掛け算をしてやると、
√3×√3
= 3
になるね。
さっき計算した、
をくっつけてやろう。
ピタっとくっつけるだけでいいんだ。
例題の(1)だったら、
(1) √12 × √32
= 2√3 × 4√2
= 8√6
になるね。
(2)は平方根だけの掛け算だからステイ。
(3)の平方根の計算は、
√48 × √27
= 4√3 × 3√3
= 12×3
= 36
になるね!
最後に、ルートをもっと簡単にできるか挑戦。
ルートの中身はいちばん簡単にすべきだからね。
例題の計算をみてみると・・・
・・・ん!?
(2)のルートはもっと簡単にできそうじゃないか??
中身の147を素因数分解すると、
147 = 3×7の2乗
になってる。
因数の7が2乗になってるじゃん??
最終的に、(2)の計算問題は、
√7×√21
= √147
= 7√3
になるね。
こんなかんじで、
ルートをもう一度簡単にできるか
チェックしてみよう!
平方根の掛け算のコツは、
ルートを簡単にして、整数と平方根をわけるってこと。
そのほうが計算が楽。
じゃんじゃんルートの掛け算していこう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenです。ハットかぶりたいね。
平方根の計算のなかでいちばんとっつきやすいのは、
掛け算
だ。
なぜなら、
平方根の計算の中でいちばんルールが簡単だからさ。
そのルールとは、
ルート同士の掛け算では中身を掛け算して一緒のルートの中にいれる
ってやつなんだ。
だから、たとえば、
(ルートa)×(ルートb)
っていう平方根の掛け算があったとしたら、
ルートab
になるってわけだ。
この計算の基本ルールを使えばルートの掛け算は簡単だ。
とりあえず、
ルートの中身をかけちゃえばいいからね。
たとえば、
(ルート2)×(ルート3)
っていう掛け算の計算があったとしよう。
さっき勉強した掛け算の基本ルールを使うと、
(ルート2)×(ルート3)
= ルート(2×3)
= ルート6
になるね!
ルートの中身をかけあわせて、ルートを1つにするだけだから、
むちゃくちゃ簡単だね。
平方根の掛け算バンザイ!
でもさ、
なんで平方根の掛け算ってこんなに簡単なのかな??
もうちょっと複雑でもいいなあー
って不満があるかもしれない。
せっかくだから、
なぜ、ルートの掛け算の基本ルールは使えるのか??
ってことを勉強してみよう。
具体的には、掛け算の基本ルールの、
(ルートa)×(ルートb)= ルートab
を証明してみるよ。
つぎの4ステップを踏めば大丈夫!
まずは、
(ルートa)×(ルートb)
を2乗してみよう。とりあえずね。
こいつらを2乗してみると、
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
になるね!
つぎは、
交換法則で掛け算の順番をチェンジしよう。
交換法則って簡単にいうと、
掛け算や足し算の順番を変えてもいいよ
っていう法則だったね。
⇒くわしくは交換法則の記事をよんでみてね
さっき2乗してできた式に注目してくれ。
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
じつは、この掛け算の式で交換法則をつかうと、
この2行めの掛け算の順番をかえてもいい
っていうことになるんだ。
だから、ルートが消えるように都合よく掛け算の順番をかえてやると、
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
= (ルートa)×(ルートa)×(ルートb)×(ルートb)
になるね!
つぎは、順番を入れ替えた状態でルートの掛け算してみよう。
ここでのポイントは、
ルートの中身が同じ平方根を2回かけるとルートがはずれる
ってことだ。
つまり、
になるってことさ。
こいつらを使ってさっきの計算をすすめてやると、
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
= (ルートa)×(ルートa)×(ルートb)×(ルートb)
= a×b
になるね!
最後に、
最初にとりあえず2乗した「2乗」をとりのぞこう!
いったん、もとにもどしてやればいいんだ。
さっきの計算式では、
{(ルートa)×(ルートb)}^2 = a×b
になっていたわけだ。
こいつの左辺の、
{(ルートa)×(ルートb)}^2
の2乗をとっぱらえばいいんだよ。
2乗の取り方は簡単!
左と右の両方にルートをかぶせちまえばいいんだ。
こんな感じでね↓↓
左のルートは中身が2乗になってるね??
こういうときは、2乗とルートがともにきえてなくなるから、
ルート{(ルートa )×(ルートb)}^2
= (ルートa )×(ルートb)
になるんだ。
よって、
(ルートa )×(ルートb)= ルート(a×b)
になるね!
おめでとう。
これでルート掛け算の基本法則を証明できたね。
ルートの掛け算??
びびることはない。
ルートとルートを1つにしちゃって、
中身をかけあわせればいいんだ。
平方根の計算は簡単だから、
なぜ、平方根の掛け算が計算できちゃうのか??
っていうことまでおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。朗読をはじめたね。
平方根の計算でよくつかうのは、
ルートを簡単にする方法
だ。
ぶっちゃけ簡単にしなくてもいいんだけど、計算しやすくなるんだ。
しかも、先生によってはルートが簡単じゃないと×にするから要注意。
そこで今日は、
平方根(ルート)を簡単にする方法
を解説していくよ。
よかったら参考にしてみて。
= もくじ =
「ルートを簡単にする」とはずばり、
ルートの中身から整数を取り出すこと
なんだ。
たとえば、
√(aの2乗×b)
があったとしよう。
ルートを簡単にするってようは、
中身の「aの2乗」をルートの外に出すことなんだ。
aの2乗をルートの外にだしてやると、
√(aの2乗×b)= a√b
になるね。
なぜなら、
√(aの2乗×b)
= √(aの2乗)× √b
= a×√b
= a√b
になるからさ。
ルートを簡単にする方法はたったの3ステップ。
例題をいっしょにといてみよう。
例題
つぎの平方根たちの中身をできるだけ簡単にしてください。
(1 ) ルート12 (2) ルート112 (3)ルート180
ルートの中身を素因数分解してみよう。
えっ。
素因数分解なんて忘れたって?!
そういうときは、素因数分解のやり方をよんでみて。
例題も素因数分解してみよう。
の根号のなかにはいってるのは、
たちだね。
こいつらを素因数分解してやると、
になる。
ルートの中から、
2乗になっている因数
をみつけよう。
例題の平方根たちをみてみると、
ってかんじで、ちらほらと2乗の因数がみつかったね。
えっ。
112みたいに4乗になっている因数がある??
そういうときは、それを「2乗した数」の2乗になっていると解釈しよう。
最後に、2乗の因数を√の外にだそう。
例題でも、2乗になってる因数をとりだすと、
になるね!
平方根を簡単にする方法はどうだった??
の3ステップで攻略できちゃうよ。
えっ、もっと高速にルートを簡単にしたい??
そんな君のために、ルートを簡単にする電卓アプリ「Simproot」をつくったよ。
よかったら試してみて。
ルートをどんどん簡単にしてこう!
そんじゃねー
Ken
中3数学では、
有理数と無理数
を勉強していくよ。
小学校ではならなってなかった新しい概念だね。
有理数
と
無理数
って1文字しか変わらないから間違いやすい。
非常にややこいね。
そこで今日は、
有理数と無理数とはなにか??
をわかりやすく解説していくよ。
= もくじ =
まずは、
有理数とはなにか??
を振り返ってみよう。
有理数とはずばり、
分数であらわせる数だ。
整数をa, bとすると、
分数 a分のb
であらわせるってことさ。
ただし、分母は「0」じゃないっていう条件あるけどね。
だって、どんな数も0で割ることはできない
っていうルールがあるからね。
せっかくだから、有理数の具体例をみていこう!
まず、有理数の例としてあげられるのが、
整数
だ。
整数ってたとえば、
1, 2, 3, 4, 5….
って1以上の整数だったり、
0
だったりするやつ。
もちろん、符号がマイナスでも大丈夫。
-1, -2, -3, -4, -5….
とかね。
こいつらが有理数なのはあきらか。
なぜなら、
整数は分母を1とした分数であらわせるからね。
たとえば、
だ。
分母を1にすれば分数であらわせる。
だから、整数は有理数なんだ。
2つめの有理数の例は、
有限小数
ってやつだ。
有限小数とはずばり、
小数の位が無限に続かないやつね。
たとえば、
0.3
とか、
0.999
とか。
こいつらって、
小数の位が無限に続いてないじゃん??
0.3だったら小数第1位でおわってるし、
0.99999だったら、小数第5位でとまってる。
こんな感じで、
ケタが続かない小数を「有限小数」ってよんでるのさ。
んで、
有限小数は有理数だよ。
なぜなら、分数であらわせるからね!
有限小数は、
(小数の位)÷(10の「小数の位の数」乗)
ですぐに分数にできちゃう。
たとえば、
みたいにね。
有限小数は「有理数」っておぼえておこう!
3つめの有理数の例は、
ってやつだ。
これは無限に小数の位がつづく無限小数のなかでも、
小数の位の続き方に規則性があるやつ
なんだ。
たとえば、
0.33333333333…..
とか、
0.123412341234….
とかね!
こいつらはじつは、分数であらわすことができるんだ。
⇒詳しくは循環小数を分数に変換する方法をよんでみて
さっきの例でいうと、
になるね!
よって、循環小数も分数にできる。
つまり、有理数ってことだね!
それじゃあ、
無理数とはなんなんだろう!??
ちょっと気になるよね。
無理数とはずばり、
分数であらわせない数
のことだよ。
「有理数では無い数」=「無理数」
ならおぼえやすいかな。
えっ。
分数であらわせない数字なんてあるのかって?!
じつはね、おおありなんだ。
具体的にいうと、
循環しない無限小数が無理数だよ。
つまり、
小数の位が続いているけど、続き方に規則がない小数のこと
だ。
そうは言っても、無理数にピンとこないね??
無理数の具体例をみていこう!
中学数学ででくる無理数の例は、
π(パイ)
だね。
直径と円周の比の円周率のことだったよね??
じつは、これ、
無限に続いてる小数で(無限小数)、
しかも、
その続き方に規則性がまったくないんだ。
試しに、円周率を100ケタぐらいみても、
3.141592653589793238462643383279502884197169399375105820974944 5923078164 062862089986280348253421170679…
・・・・っダメだ。。
規則性もクソもねえ!ランダムにケタが続いているよね。
こういうやつが、
無限小数で、しかも、循環しない小数
つまり、無理数ってわけ。
中3数学でならった
「平方根」
も無理数だよ。ルートとよばれてるやつだ。
ルートがついているやつはたいてい無理数だね。
たとえば、良く登場してくる、
ルート2
は圧倒的に無理数だね。
なぜなら、
無限につづく小数で、しかも規則性がないからね。
こっちも試しにルート2の小数のケタをかきなぐってみると、
1.4142135623 7309504880 1688724209 6980785696….
まじムリっ!
ぜんぜんケタの繰り返しに規則性がみつけられないじゃん!?
だから、
ルート2は無理数
といえそうだ。
でもね、ルート2が平方根だからといって、
√(ルート)がついている数字はぜんぶ無理数ってわけじゃない。
たとえば、ルート4をみてみよう。
こいつには一見、無理数の香りがする。
ルートがついてるし。
だけどね、こいつは無理数じゃない。
なぜなら、
ルート(√)がはずせちゃうからね。
√の中身の4は「2の2乗」。
ってことは、√4の根号ははずせちゃうね。
√をはずしてみると、
√4 = 2
になる。
つまり、√4の正体は整数の2ってことなのさ。
整数は有理数だったね??
ってことは、
√4も有理数なのさ。
√がついてるからといって、無理数と決めつけないようにしよう!
ルートがはずれるか確認してみてね。
有理数と無理数の違いはピンときたかな?
こいつらの違いは、
っておぼえておけば大丈夫。
有理数と無理数を見分けられるようにしよう!
そんじゃねー