こんにちは！この記事をかいているKenだよ。弾丸旅行にはまっているね。
180°×(n-2)
で計算できたね。
ここで、好奇心旺盛なヤツはこう思うはずだ。
そう。
そうだ。
多角形の外角の和はいくつになるんだろう！？？
ってね。
今日はそんな疑問にこたえるため、
多角形の外角の和の求め方をわかりやすく解説していくよ。
よかったら参考にしてみてね。
結論からさきにいっちゃおう。
多角形の外角の和（n角形）はずばり、
360°
だ。
三角形の外角の和は360°。
四角形の外角の和も360°。
なんと、八十角形の外角の和も360°だ。。
いや、むしろ、
こんなんでも、
あんなんでも、
外角の和は360°になっちゃうんだ。
だから、
外角の和を求めなさい！
っていう問題がでたら、ドヤ顔で、
360°ですけどなにか？
っていってやろう。
多角形の外角の和は360°ってことはわかった。
むちゃくちゃわかりやすいね。
ただ、ここで知っておいてほしいのは、
なぜ多角形の外角の和が360°になるのか？？
ってことさ。
こいつを知っていると、
たぶん、
モテルね。
たとえば、
n角形があったとしよう。
1つの頂点に注目してみると、
「内角」と「外角」で1つの直線になっているよね？？
つまり、
内角 + 外角 = 180°
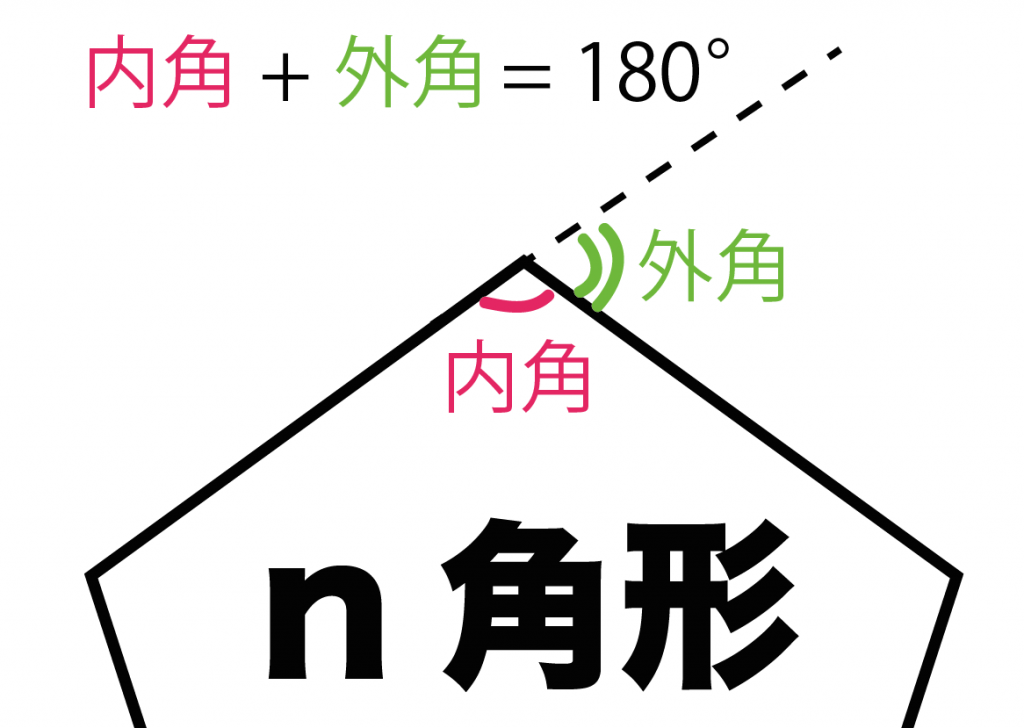
になっているってわけさ。
これは全頂点で同じことが言えるから、
内角と外角をぜーんぶ足し合わせたら、
180n
になるはずだ。
「内角と外角の和」から「内角の和」をひいてやると、
「外角の和」になる。
多角形の内角の和（n角形）は、
180(n-2)
だったよね？？
よって、
（内角と外角の和）- （内角の和）
= 180n – 180(n-2)
= 360°
になるね。
つまり、
多角形の外角の和（n角形）は、
360°になるんだ！
この数字にはnがふくまれてないから、
何角形でも外角の和は360°になるんだ。
多角形の外角の和はシンプル。
いつでも、
どんな多角形でも、
360°になるんだ。
テストで間違わないようにおぼえておこう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。映画は1日2本までだね。
正多角形の内角を知りたいときってあるよね？？
多角形の内角の和は公式つかえばドヤ顔できるけど、
せ、正多角形の内角はどうすれば・・・？？
ってなるよね。
そんな流れで、
正多角形の内角の求め方を解説していくよ。
よかったら参考にしてみてね。
正多角形の1つの内角の大きさを求めたいときは、
つぎの公式をつかってみて。
正n角形の1つの内角は、
180°（n-2）/ n
で計算できちゃうって公式だ。
さっそく、正五角形の内角を計算してみよう！
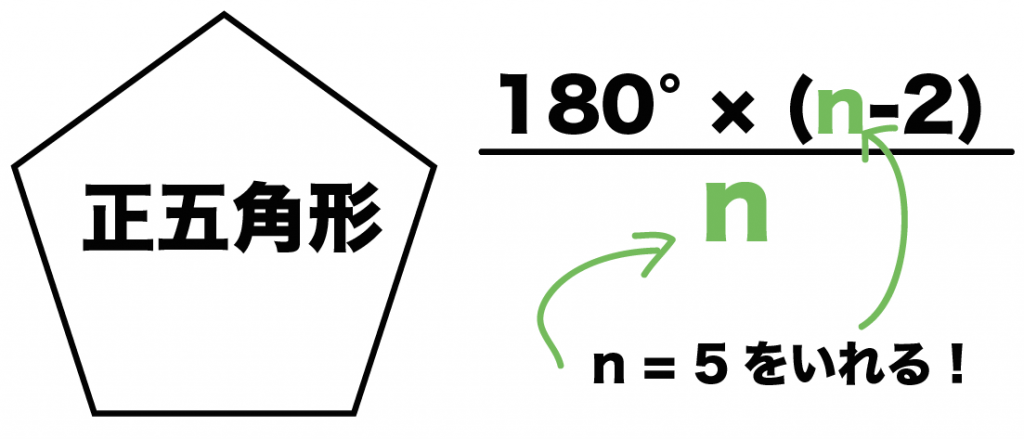
正五角形は頂点が5つあるから、
さっきの公式のnに「5」をいれるだけでいいんだ。
すると、
180 × (n-2)/n
= 180×(5-2)/5
= 108°
になるね。
つまり、
正五角形の内角の大きさは「108°」ってことさ。
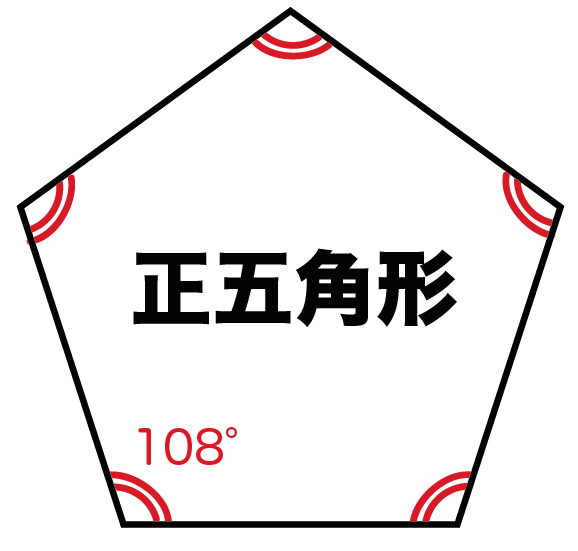
くそ便利でしょ？？。
でもでも、なんで、
180× (n-2)/n
で計算できちゃうんだろう？？
都合よすぎるよね？。
なぜそうなるの？？
ってことを確認してみよう。
正多角形の内角をぜーんぶ足したらどうなる？？
って考えてみて。
多角形の和の公式を使うと、
正n角形の内角の和は、
180°×（n-2）
になるよね。
正多角形の特徴の1つに、
内角の大きさはすべて等しい
ってものがある。
たとえば正五角形を考えてみよう。
5つの内角を、
とすると、
a = b = c = d = e
になるんだ。
だから、
正多角形の1つの内角の大きさを出したいときは、
内角の和を頂点の数でわればいいんだ。
内角の和「180°×（n-2）」を、
頂点の数「n」でわると正多角形の1つの内角の大きさになるよ。
180× (n-2)/n
どの内角も同じ大きさだからね！
正多角形の内角の公式は、
180°×（n-2）/n
だったね。
ようは、
「内角の和」を「頂点の数」でわればいいんだね。
よくでる問題だからテスト前に復習してみてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。チキン、うまいね。
五角形の内角の和って何度だろう？？
ときどき、そんなこと考えちゃうよね。
そんなときは、
多角形の内角の和の公式をつかえば大丈夫。
たぶん、3秒で計算できるよ。
180°×（n-2）
っていう公式のnに「5」を代入してあげる。
すると、
180°×（5-2）
= 540°
になる。
つまり、
五角形の内角の和は「540°」ってことさ！
公式をつかえば1秒ぐらいで計算できそうだけど、
そもそもなんで「540°」になってるんだろう？？
チョー気になるよね。
その理由は、
五角形の中に三角形が3つも潜んでいるからなんだ。
まず、
対角線を2本ひいてみよう。
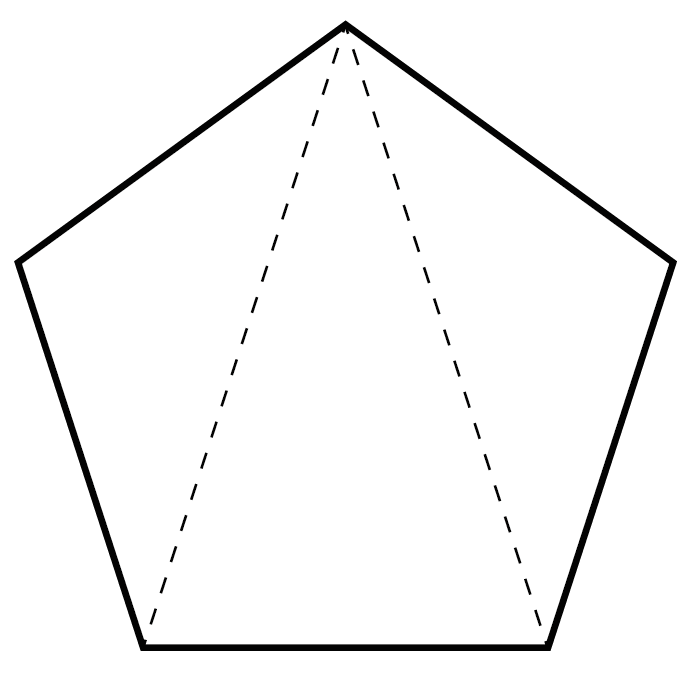
すると、どうだろう？？
三角形が3つも隠れていることがわかるよね。
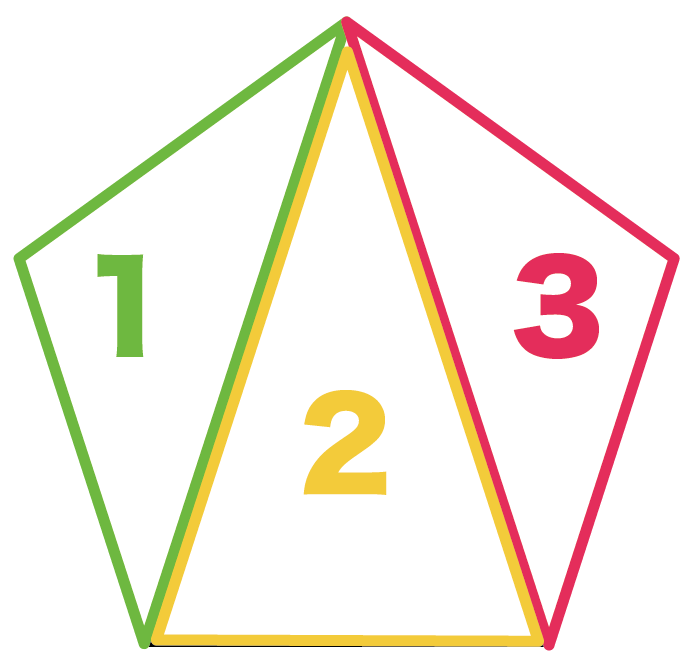
三角形の内角の和は「180°」で、5角形には三角形が3つもかくれているんだ。
よって、
五角形の内角の和は「三角形の内角の和（180°）」を3倍した
180°×3
= 540°
になるのさ。
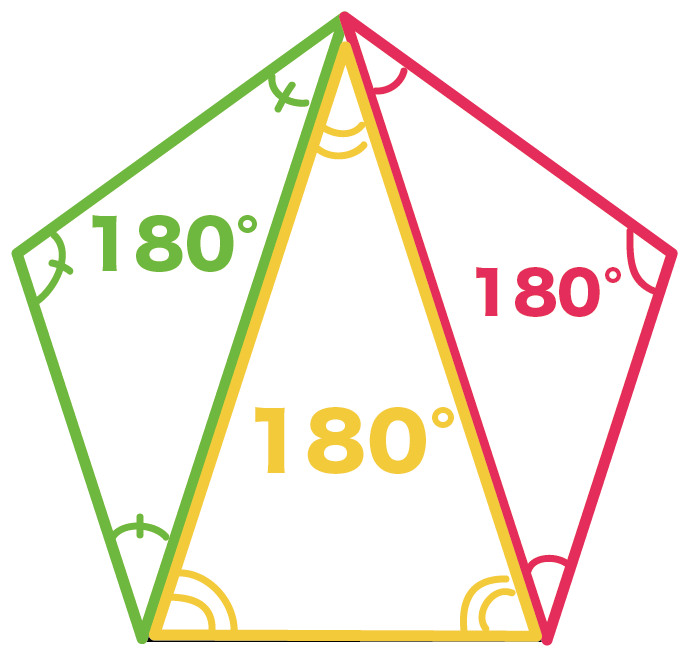
五角形の内角の和を求めるときは、
180°×（n-2）
のnに5を代入しよう。
テストにでやすいから復習しておいてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。パイプユニッシュ、ほしいね。
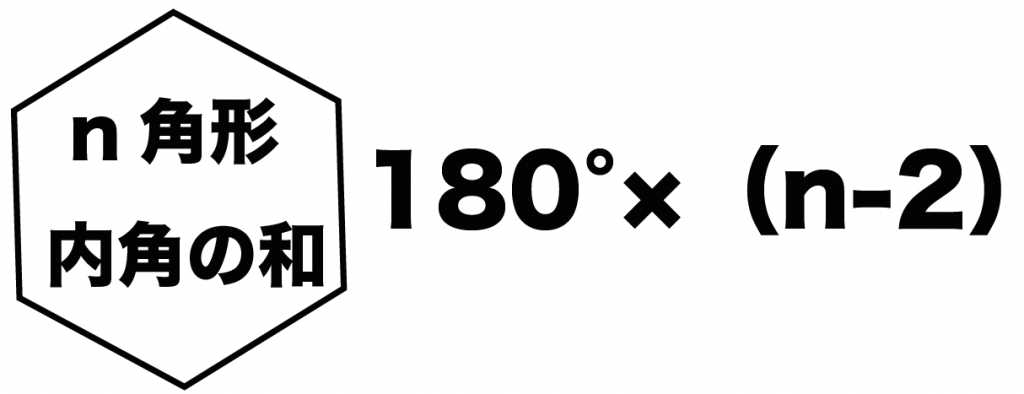
多角形の内角の和の公式ってめちゃ便利。
n角形の内角の和を求めたいときは、
180°× (n -2)
で計算できちゃうのさ。
たとえば、
五角形の内角の和を計算したいときは、
nに「5」を代入すればいいんだ。
180°×（5-2）
= 540°
になるね。
つまり、
五角形の内角をぜーんぶたしたら540°になるってわけさ。
多角形の内角の和の公式
180°×（n-2）
では、
をあらわしているよ。
三角形の内角の和は「180°」ってならったから、
多角形の中に何個の三角形がひそんでいるか？？
をあばいてやればいいってわけさ。
三角形の中には三角形が・・・1つ！
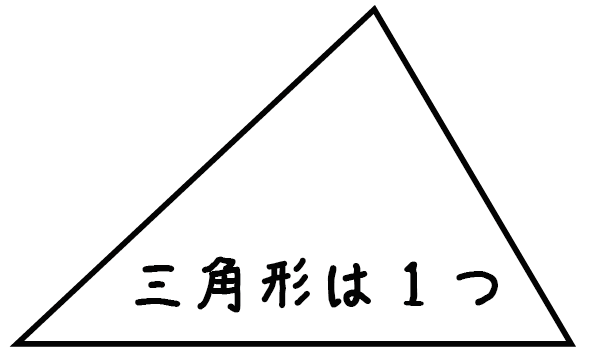
四角形の中には三角形が・・・2つ！
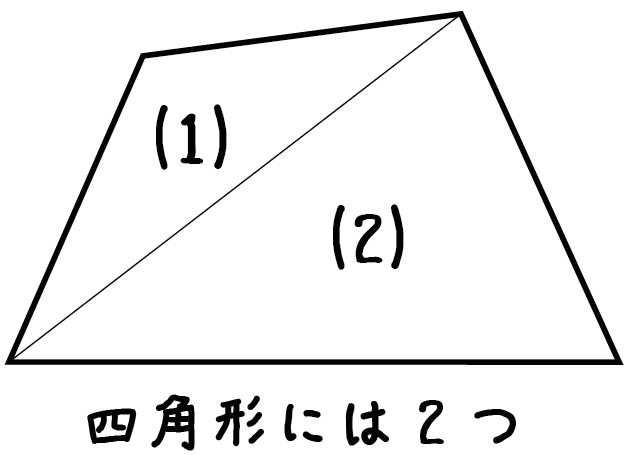
五角形の中には三角形が・・・3つ！
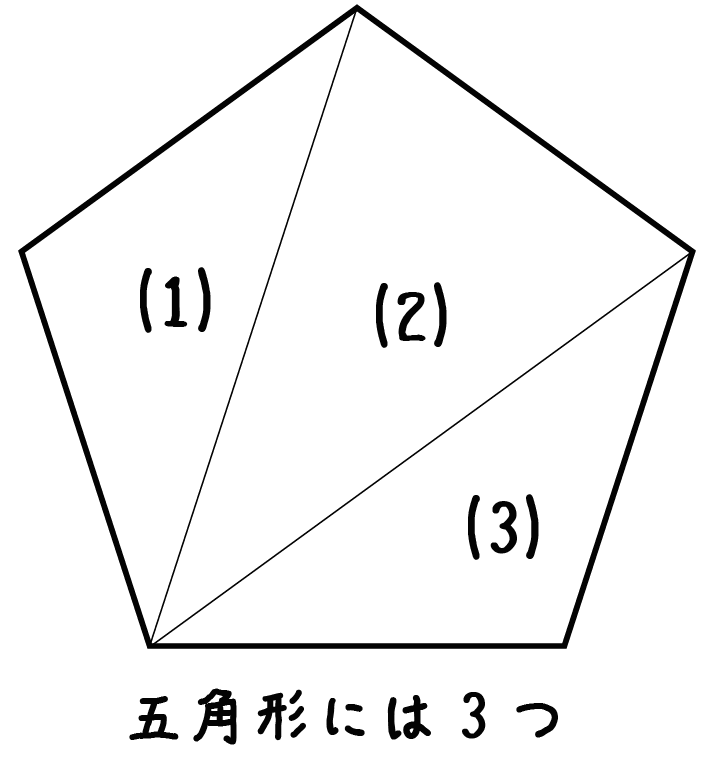
六角形の中には三角形が・・・4つ！！
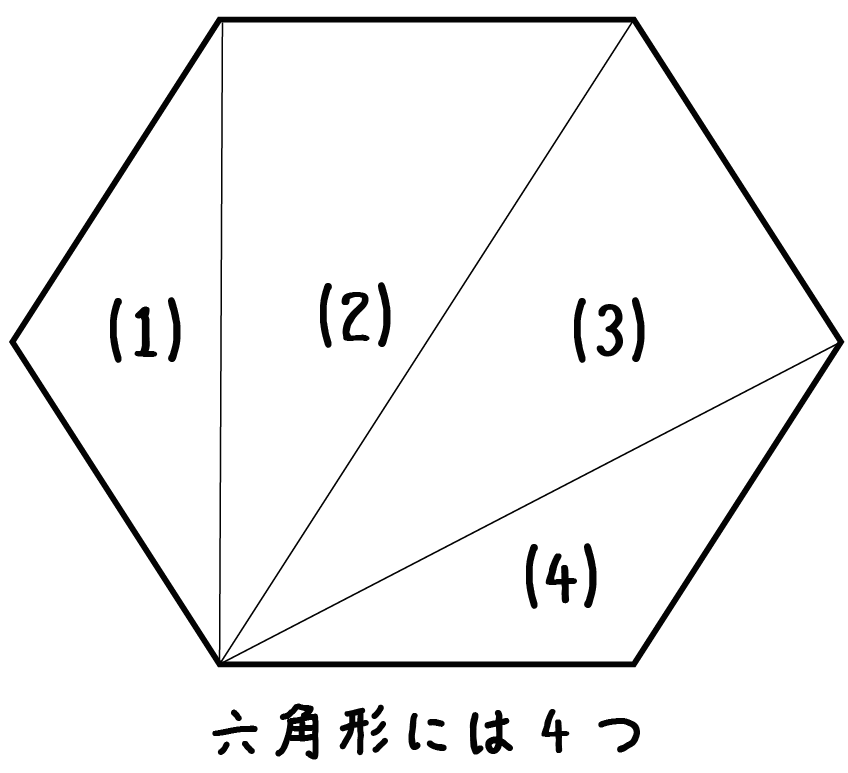
七・・・・
ふう。
六角形まで確かめてみて「あること」に気づかない？？
そう、じつは、
多角形には「角の数 -2」個の三角形がひそんでいるんだ。
「五角形」だったら、
「5」から「2」をひいた「3」個の三角形がかくされているというわけさ。
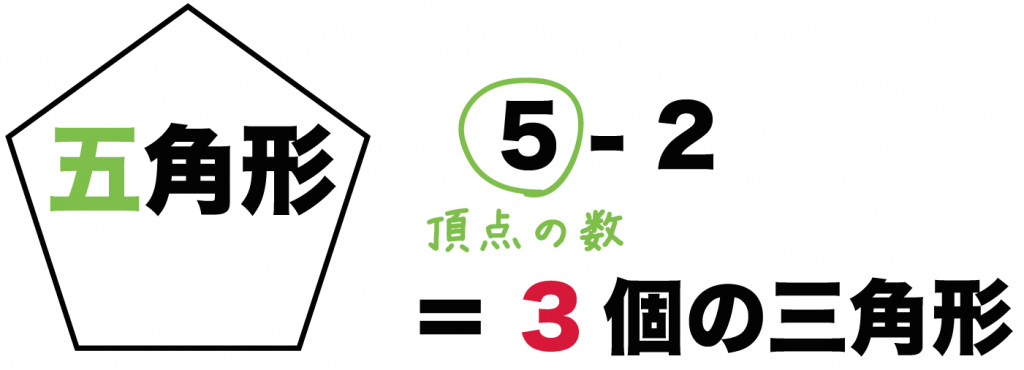
n角形のときは（n-2）個の三角形がかくれているというわけさ。
三角形の内角の和は180°だから、
(n-2)個の三角形がかくれている多角形の内角の和は、
180°× (n-2)
になるのさ。
だから、五角形の内角の和は、
180°×（5-2）
= 540°
になるんだね。
n角形の内角の和は、
180°×（n-2）
で計算できちゃうんだ。
内角の和をじゃんじゃん求めてみよう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。スイカの種をうめたね。
「鋭角三角形」ですか？？
それとも、
「鈍角三角形」ですか？？
って問題が、ある。
しかもけっこう、ある。
言葉をよーく理解していないと、答えられないタイプのやつだ。
今日はこの手の問題を瞬殺するために、
鋭角三角形と鈍角三角形をみわける3つのステップ
を伝授しよう。
よかったら参考にしてみてね。
みわけ方はむちゃシンプル。
つぎの、
イエス・ノー クエスチョン
に答えていけばいいんだ。
質問はたったの2つさ↓↓
イエス・ノーで答えてみてね。
三角形の内角に、
直角(90°)
がないか確認しよう。
もし、90°が1つでもみつかれば、
ただの直角三角形だ。
そいつは鋭角三角形でも鈍角三角形でもない。
たとえば、つぎの三角形ABCだね。
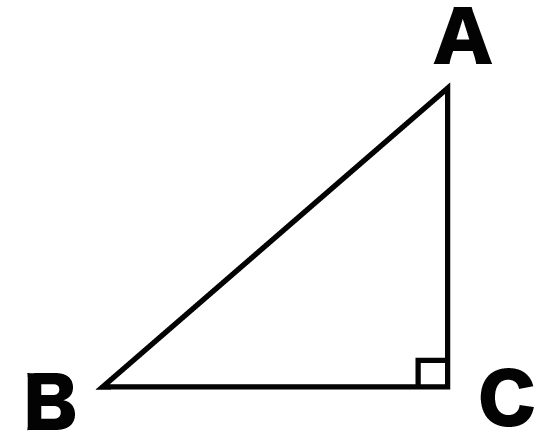
こいつはまぎれもなく直角三角形だ。
だって、角Cが90°になってるからね。
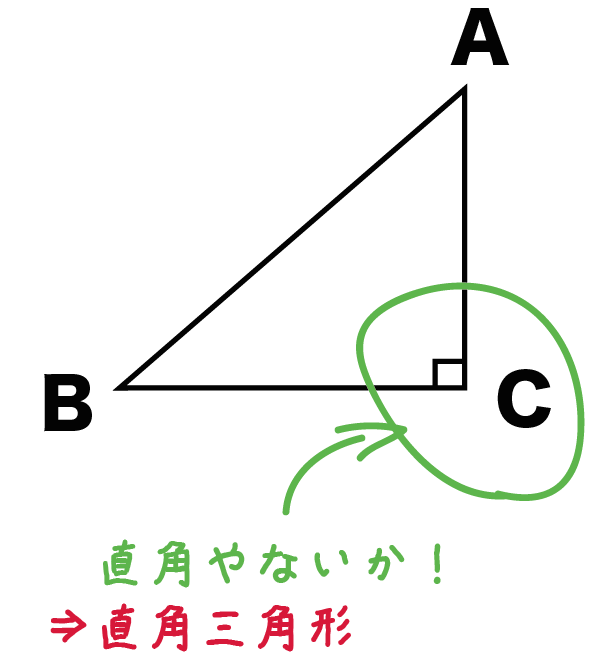
内角に1つでも90°があったら直角三角形
とおぼえておこう！
つぎに、
鈍角（90°よりも大きい角）がないか確認しよう。
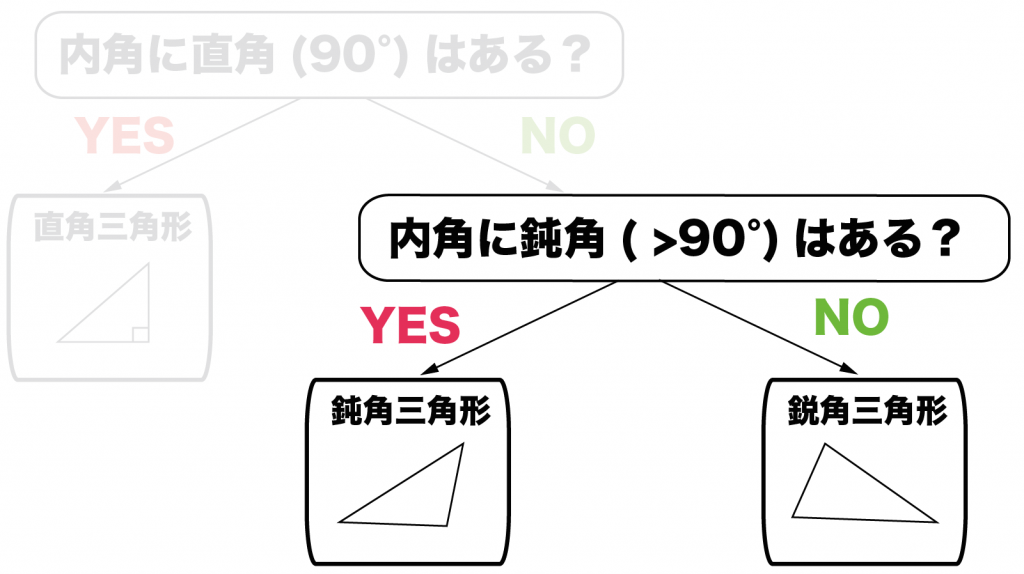
鈍角を持っている三角形は、
まぎれもない鈍角三角形だ。
たとえば、つぎの三角形ABCだね。
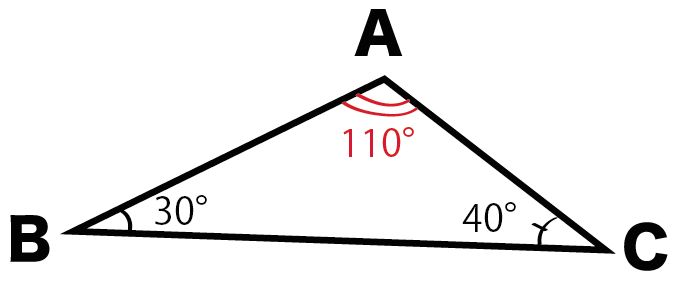
こいつは鈍角三角形だね。
だって、角Aが110°だからさ。
90°（直角）よりも大きいでしょ？？
こんな感じで、
鈍角を持っている三角形は「鈍角三角形」ってことをおぼえおこう！
直角三角形でも鈍角三角形でもないヤツは、
「鋭角三角形」さ。
教科書によると「鋭角三角形」とは、
3つの内角がすべて鋭角である三角形
とかいてあるね。
正直、
三角形の内角をぜーんぶ調べるのはメンドイ。
それよりは、
直角三角形と鈍角三角形である可能性を消してやるとラクなんだ。
だから、
上の2つの質問、
にすべて「No」なら、
そいつは「鋭角三角形」ってことさ。
たとえば、下のやつは「鋭角三角形」だね。
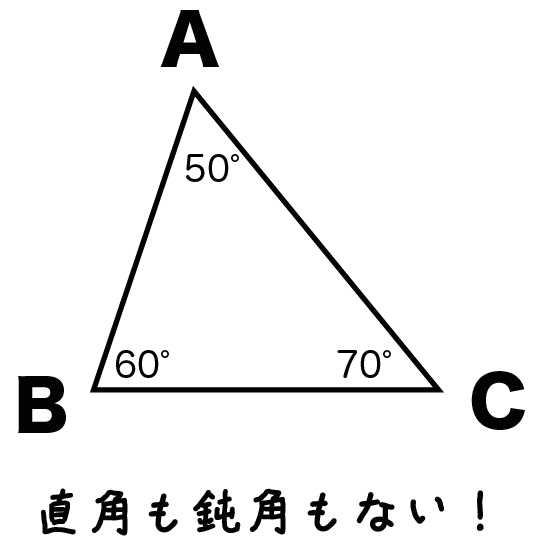
だって、直角も鈍角もないからさ。
消去法で「鋭角三角形」ってこと！
鋭角三角形と鈍角三角形の見分けかがわかったね。
イエス・ノークエスチョンをするだけでいいんだ。
授業やテストできかれたら、
ドヤ顔で答えてやろう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。ミントティー、最高。
図形には、
いろいろな角度があるよね？？
鋭そうな角だったり、
鈍そうな角度だったりする。
するどい角なら鉄にも刺さりそうだし、
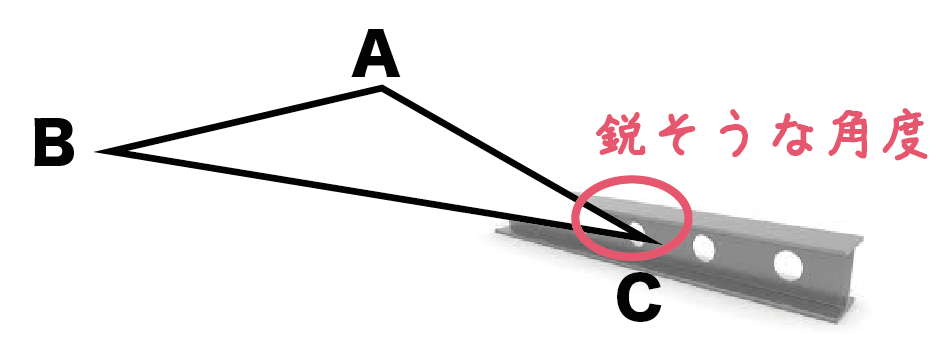
にぶい角だったら豆腐にしかさせないかもしれない。
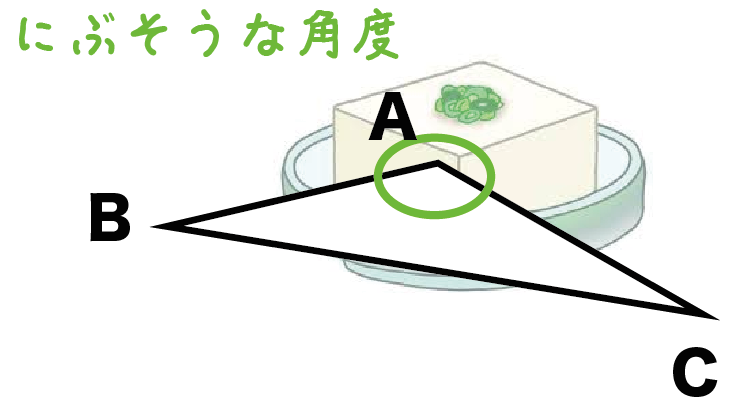
数学を勉強していると、
「鋭角」と「鈍角」っていう言葉を勉強するけど、
何を基準に「鋭い」とか「鈍い」とか言ってるんだろう？？
今日はこれを詳しく勉強していくよ。
ずばり、
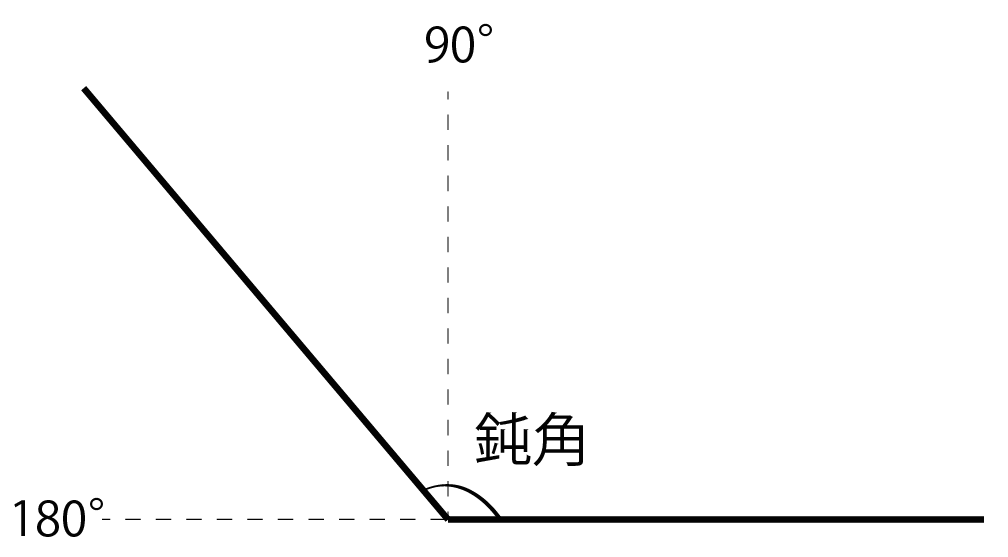
「鋭角」と「鈍角」の基準は、
「90°よりも小さいか、大きいか」なんだ。
90°より小さい角のことを「鋭角」といい、
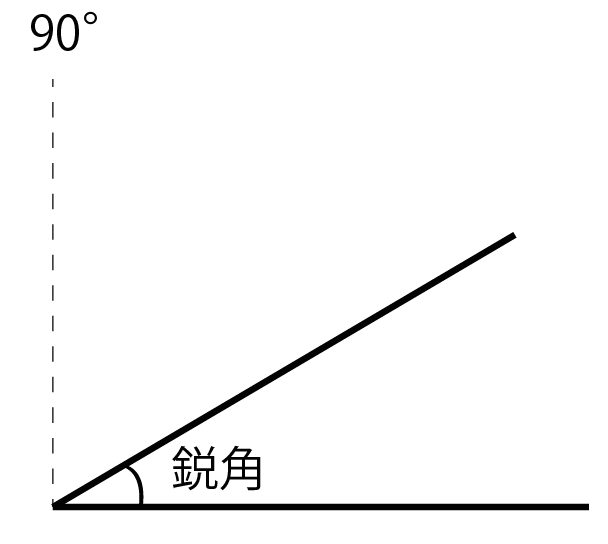
90°ぴったしの角を「直角」というね。
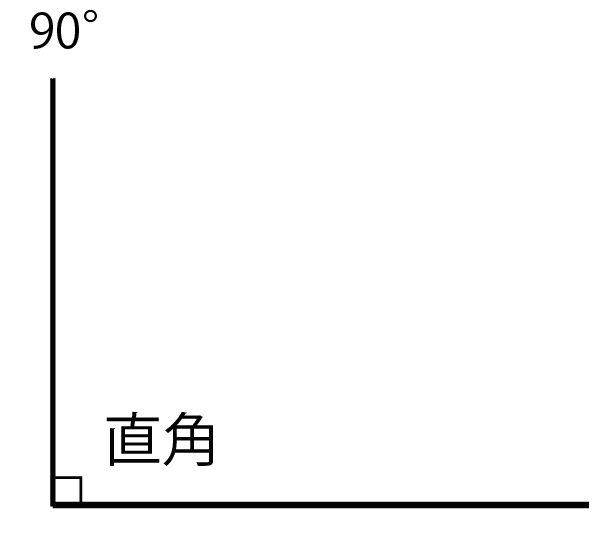
さらに、
90°より大きくて180°よりも小さい角を「鈍角」っていうんだ。
人間にもいるよね。
「するどいヤツ」とか「にぶいヤツ」とか。
その基準は人によって違うと思うんだ。
恋を察するのが速いと「するどい」っていわれたり、
オヤジギャグがわからないと「にぶい」っていわれるかもしれない。
数学みたいに「鋭い・鈍い」の基準なんてない。
うん、ないよ。
だから、数学の「鋭角」とか「鈍角」っていう考え方はわかりやすいね。
「90°」よりも「小さい」か「大きい」かを判断すればいいんだもの。
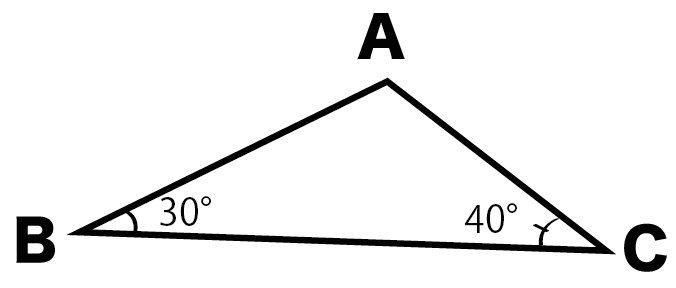
例題をといてみよう。
順番にみていくよー！
まず角Bをみてみよう。
よーく注目してみると、
30°
であることがわかる。
これは明からに90°よりも小さいよね？？
こいつは「鋭角」だ。
Cをクローズアップしてみると、
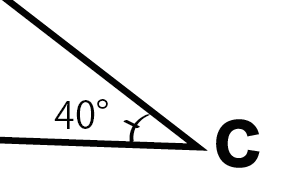
40°
であることがわかる。
こいつはどっからどうみても90°より小さいから、
「鋭角」だね。
さあて、残るは角Aだね。
三角形の内角の和は180°なので、
180°から「角B (30°)」と「角C（40°）」をひいてあげよう。
そうすれば角Aが計算できるはずだ。
角A ＝ 180° – 30°（角B）- 40°（角C）
＝ 110°
になる。
これは明らかに90°よりも大きいし、180°よりも小さいよね？？
ってことはコイツは、
「鈍角」になるよ！
「鋭角」と「鈍角」の分かれ目は、
90°より大きいか小さいか、だ。
90°を片手にガンガン鋭角・鈍角をみつけていこう。
鋭角と鈍角の違いにピンときたら、次は「鋭角三角形と鈍角三角形をみわける方法」をマスターしてみてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。福岡タワー、いいね。
三角形の外角の定理って知ってる？？
教科書によると、
三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。
っいう定理があるらしいんだ。
たとえば、
内角60°と30°の三角形があったとしよう。
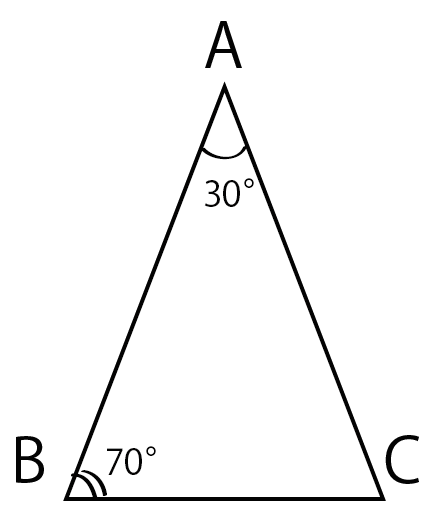
このとき、
角ACD
＝角BAC + 角ABC
＝ 30° + 70°
＝ 100°
になるんだ。
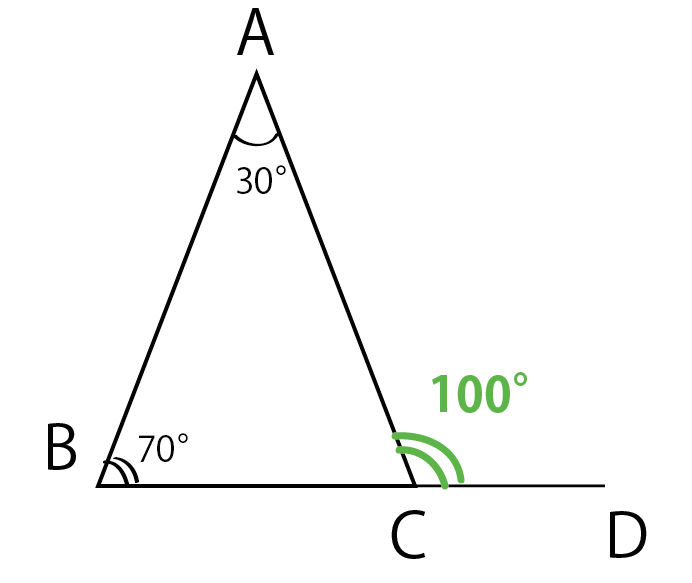
今日は、この三角形の外角の定理が、
なぜ使えるのか？？？
ということを証明していこう！
三角形の内角の和の証明と同じやり方だよ。
平行線の性質をうまく使って、
三角形ABCの外角の和がa + bになることを証明してみよう！
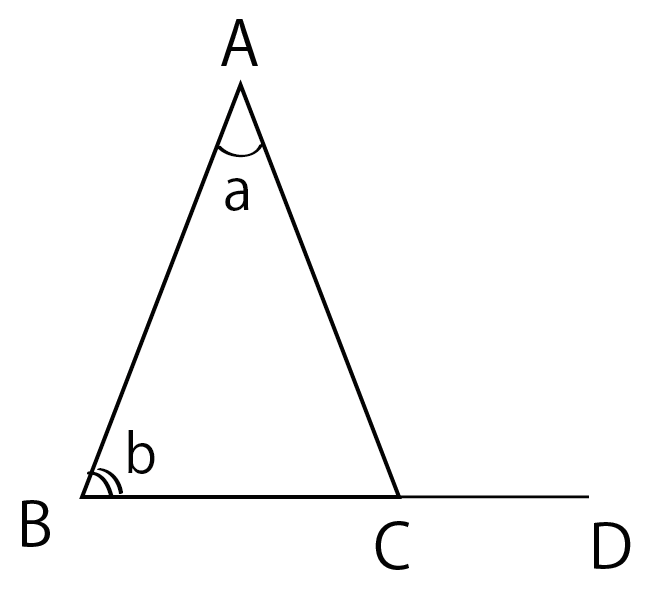
外角の頂点に平行線をひいてみて。
三角形ABCでいうと、
点Cを通る辺ABと平行な直線をひくことになるよ。
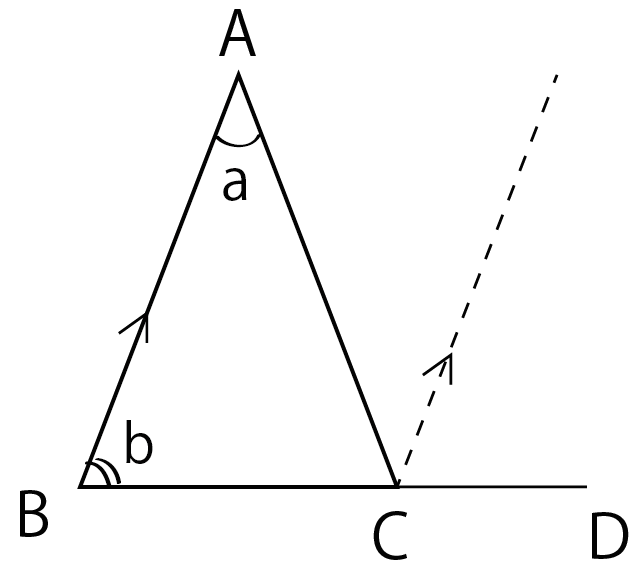
まず仕込みは完了だ。
つぎは平行線の性質をつかってみよう。
平行線の性質って、
の2つだったね。
この性質をつかってやると、
三角形の外角である角ACDは、
角ACD = a + b
になるよね。
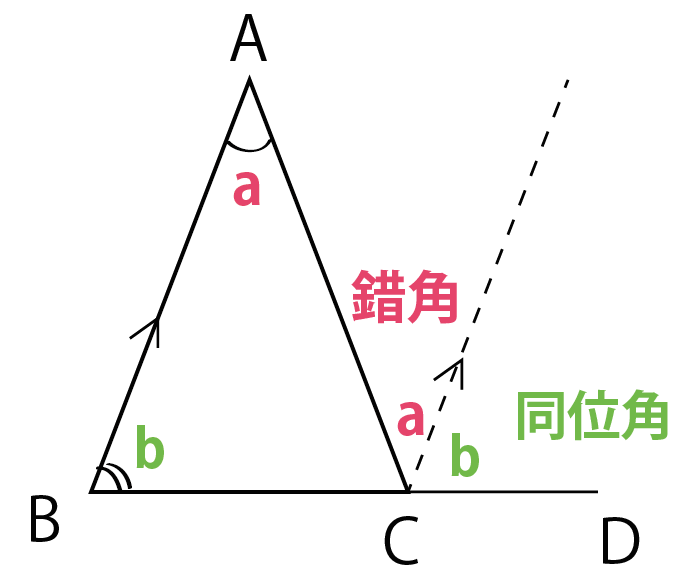
つまり、
三角形の1つの外角は、となりあっていない残り2つの内角の和に等しい
といえるのさ。
三角形の外角の定理はいっぱいでてくるよ。
テストでもガンガン使っていこう！
証明も自分でできるとなおよしだね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。天満宮にいきたいね。
三角形の内角の和は「180°」になる
って知ってた？？
つまり、
中の角度をぜんぶ足すと180°になるってことさ。
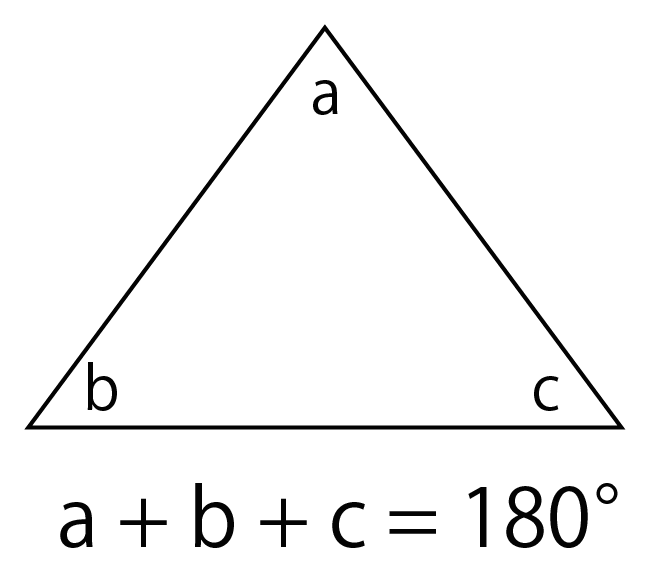
これはこれで、
うわーすげーー
ってなるよね？。
ただ、いちばん大切なのが、
なぜ、三角形の内角の和が180°になるのか？？
ってことだ。
これを知っていればクラスでモテるかもしれない。たぶん。
そこで今日は、
三角形の内角の和の求め方の証明
を3ステップで解説していくよ。
よかったら参考にしてみて。
さっそく証明していこう。
三角形ABCをつかっていくよ。
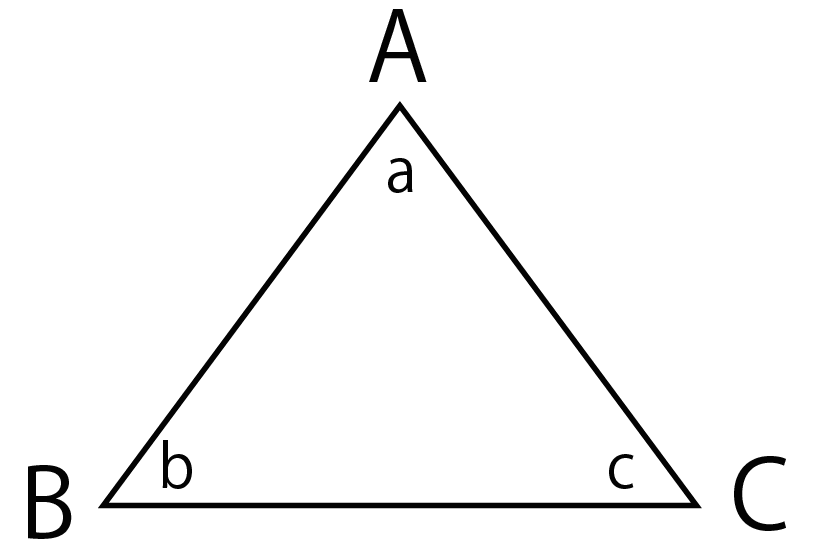
まずは底辺を右にすーっと伸ばしてみて。
三角形ABCでいうと辺BCだね。
こいつを右にのばして、
伸ばした先を、なんだろうな、Dとでもおこう。
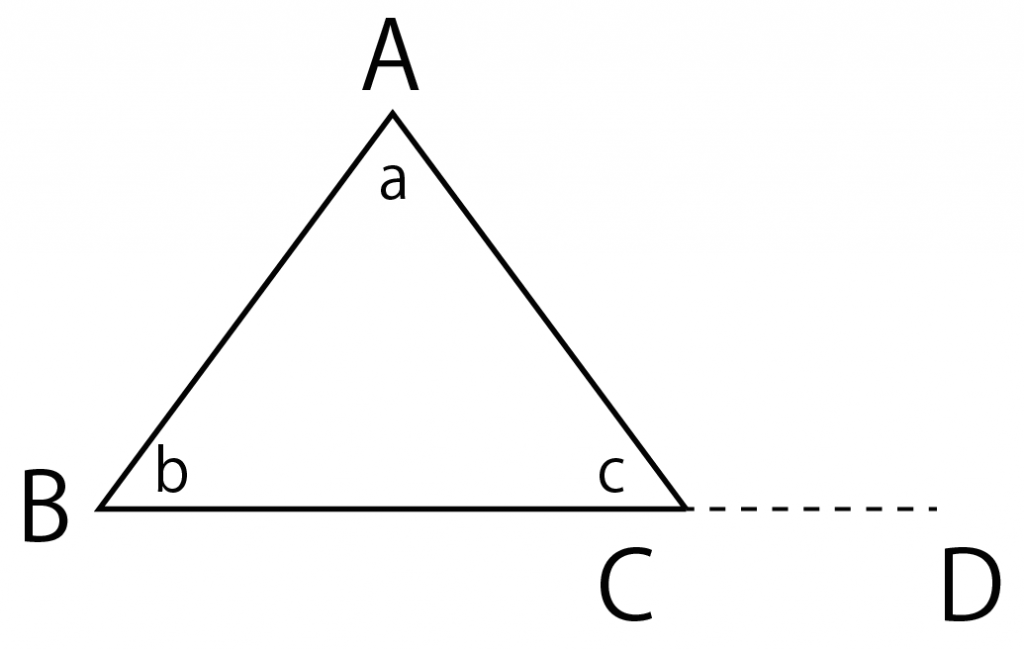
これがはじめの一歩さ。
つぎに平行線を一本ひくよ。
伸ばした底辺の頂点を通る平行線をひいてみて。
向かい側の辺に平行な直線ね。
三角形ABCでいうと、
Cを通ってABに平行な直線だね。
そうだなあ、平行線の先をEとでもおこうか。
これが第2ステップ。
最後に平行線の性質をつかっちゃおう。
平行線の性質って、
の2つだったよね？？
これを平行線でつかってやればいいんだ。
三角形ABCではABとCEが平行だったね。
錯角は等しいから、
角BAC ＝ 角ACE
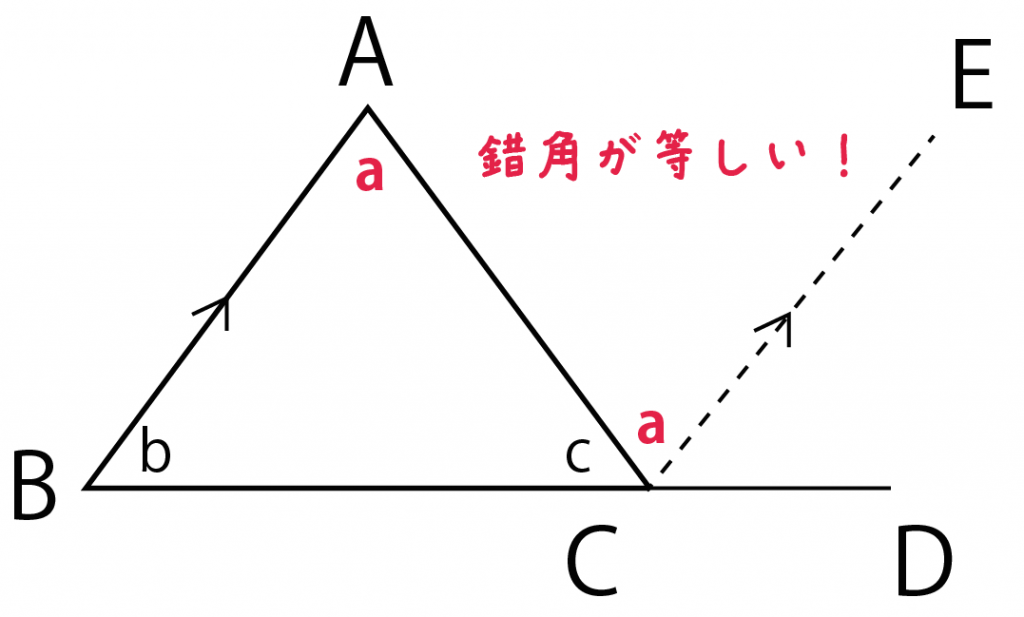
になる。
また、同位角をつかってやれば、
角ABC ＝ 角ECD
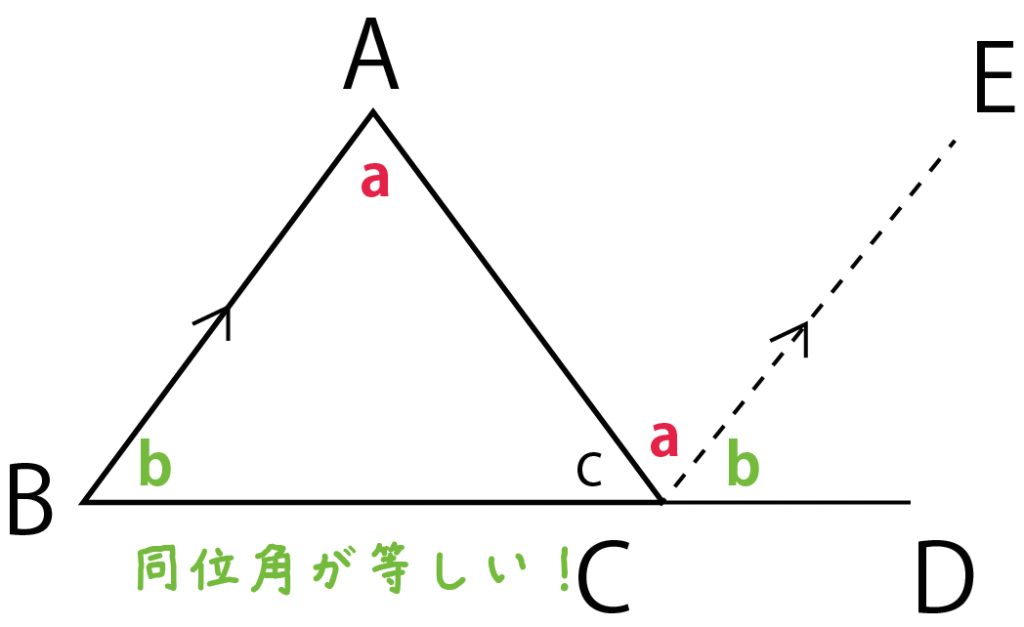
になるね。
ここで、
頂点Cに注目してみて。
この頂点には
という3つの角度があつまっているよね。
そんで、3つで1つの直線になっている。
ってことは、
ぜーんぶ足し合わせたら180°になるってことさ。
つまり、
a + b + c ＝ 180°
ってことがいえるね。
「a + b + c」は三角形の内角をぜんぶたした和。
だから、
三角形の内角の和は180°になる
ってことが言えるのさ。
三角形の内角の和の証明は、
平行な補助線をひくことがポイント。
ここさえできればあとはお茶の子さいさいさ。
テストにも出やすいからよく復習しておいてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。川にはまっているね。
平行線が2本あったとしよう。
名は、
「直線l」と「直線m」
という。
ある日コイツらに、
直線nが交わったとしよう。そう、いきなりだ。
もちろん、平行線の直線lとmはビックリしている。
だけど、この時点で、
平行線の性質
がつかえるようになる。
それは、
2つの直線に1つの直線が交わっているとき、
という性質だ。
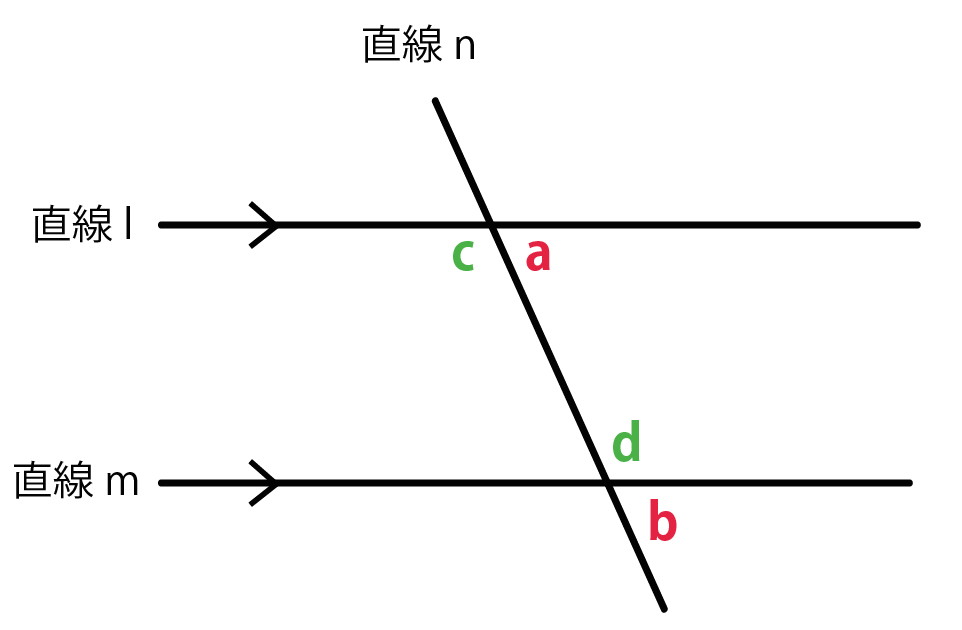
図でいうと、
だね。
今日は平行線の性質をつかって、
問題をといてみよう！
つぎの問題をといてみよう。
例題
下の図で、l // m のとき、角度x の大きさを求めなさい。
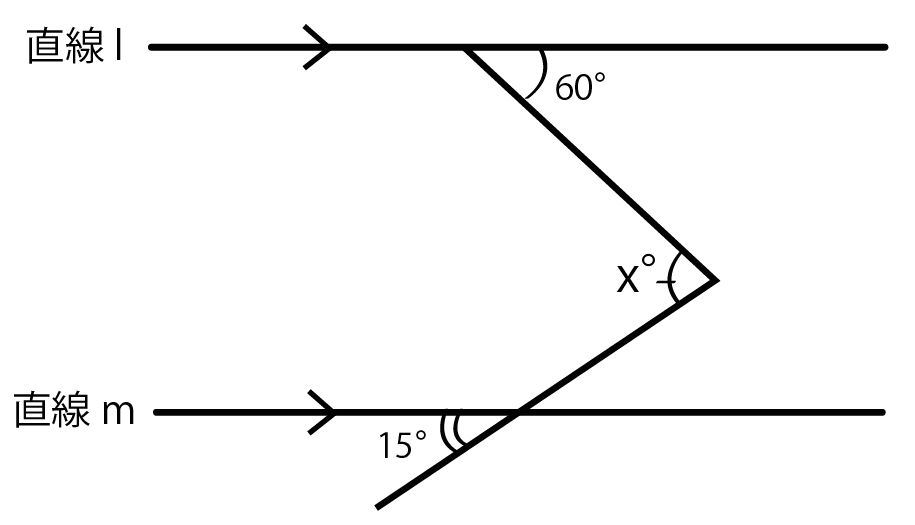
この手の問題は3ステップで攻略できちゃうよ。
直線lとmに平行なnをひいてあげよう。
ひく場所は、
角xの頂点のところだ↓↓
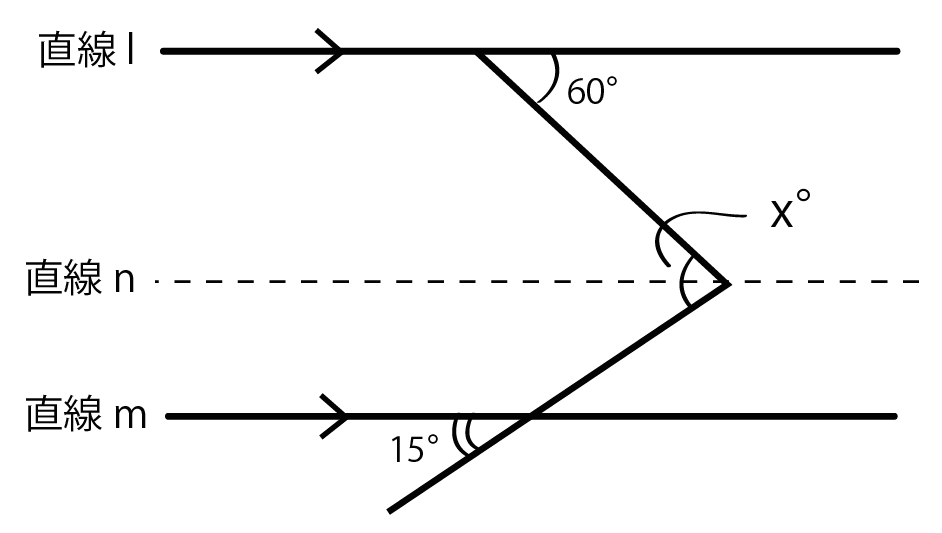平行線の性質をつかうために、平行線を増やしたわけさ！
平行線の性質の、
同位角が等しい
を使ってあげよう。
直線mとnに注目してみて。
コイツらで同位角が等しいことをつかってやると、
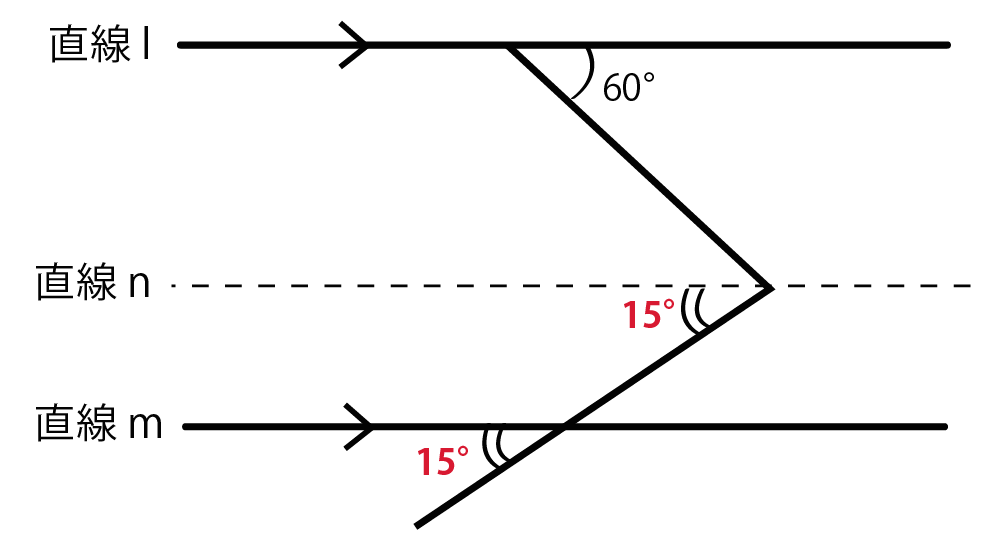
角xの下半分が15°になるね。
あともう少し！
つぎは、
錯角が等しい
という性質をつかおう。
直線lとnに注目してみて。
2つの直線は平行線だから、
錯角が等しいことをつかってみよう。
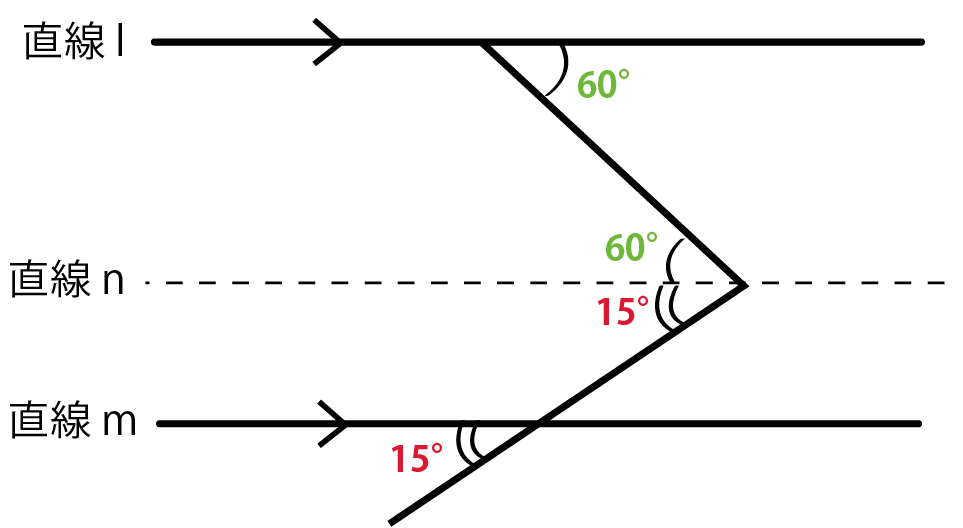
すると、
角xの上半分は60°になるね。
ってことで、
Step2と3の角たちをたすと、
角度x ＝ 75°
になる。
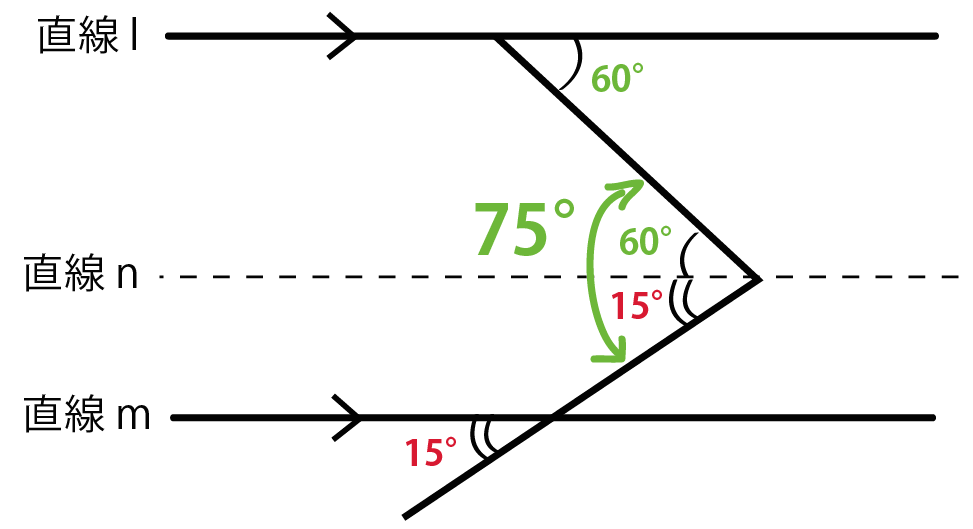
これで問題クリアだよ。おめでとう。
平行線の性質である、
はむちゃくちゃ便利。
ポイントは、
足らなかったら平行線を増やす
ということ。
これにつきるね。
必要だったら平行線をじゃんじゃん追加しよう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。男はだまってアイスティーだね。
中学2年生になると、
「同位角」と「錯角」
を勉強するよね？？
直線nがlとmと交わっているシチュエーションを想像してくれ。
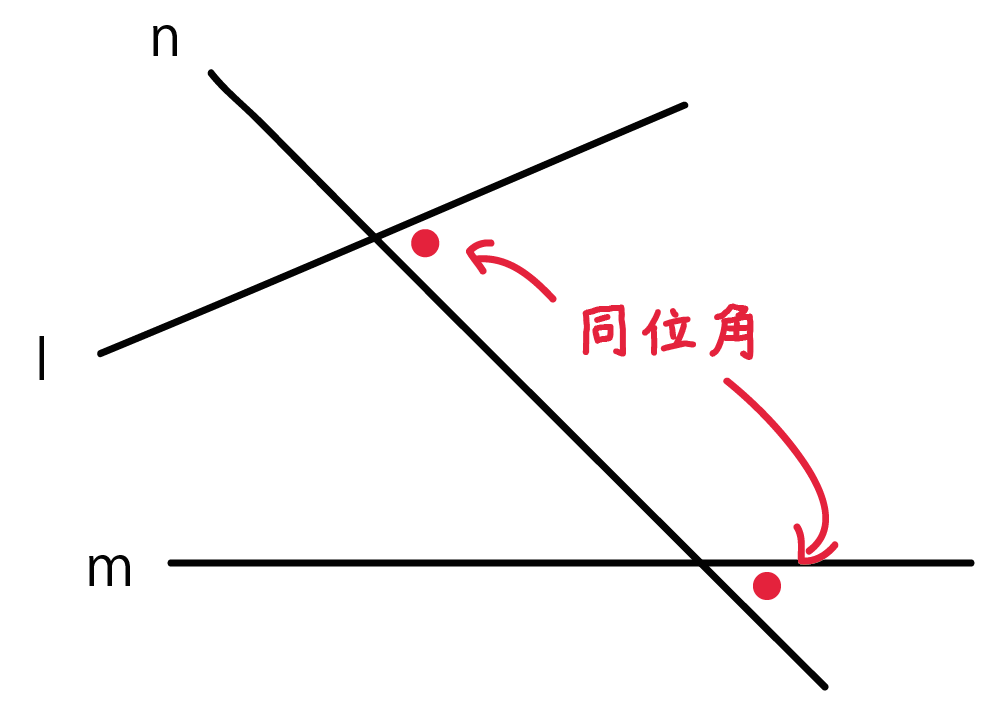
このとき、
2つの赤い角のことを「同位角（どういかく）」といい、
緑の角のことを「錯角（さっかく）」というんだ。
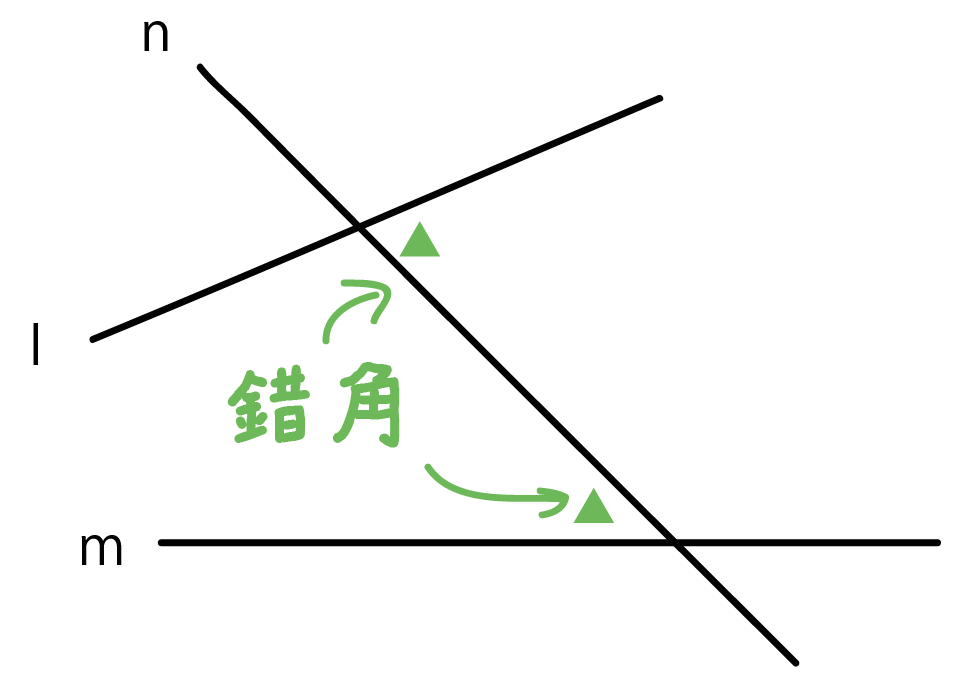
この2つはむちゃくちゃ重要。
10分に一回ぐらいでてきそうなぐらいな勢いでね。
だけれども、
問題がひとつだけ、ある。
それは、
同位角と錯角がごっちゃまぜになりやすい
ってことさ。
今日はややこしい問題を解決するために、
一生忘れない同位角と錯角の覚え方を伝授するよ。
困ったときに参考にしてみてね。
まずは同位角の覚え方から紹介するよ。
同位角の覚え方はずばり、
「同じイの角度」
だ。
えっ！？ わけわかんねえけど？？
ってキレそうになってるでしょ？。
うん、わかるよ、その気持ち。
これから詳しく説明していこう。
3直線の交点にカタカナの「イ」を同じ向きで置いてみて。
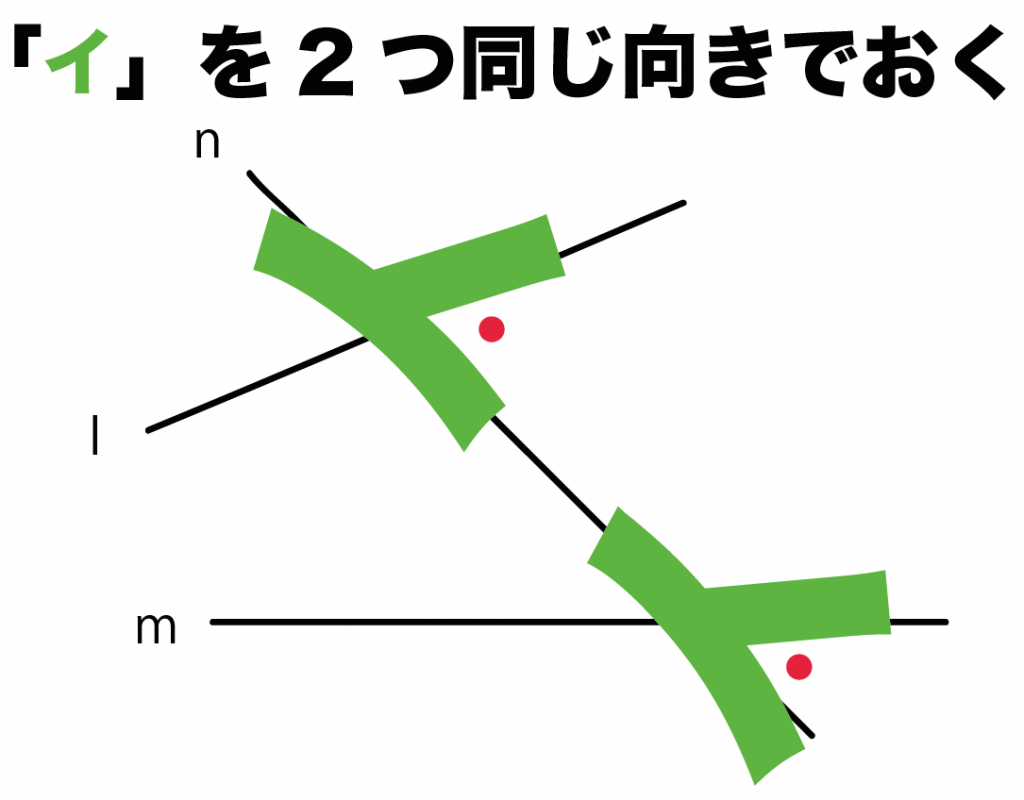
するとどうだろう？？
同位角の2つの赤い角って、
「イ」の同じ角度だよね？？
「タテ棒」と「斜めの棒」の間の角度ってことさ。
同位角をさがしたいときは、
「イ」を直線の交点に同じ向きでおいてみて、
「イ」の同じ角度になっているか確かめればいいんだ。
ガンガン「イ」をおいてみよう！
錯角の覚え方は語呂をつかうよ。
想像力で暗記しちまおうってわけさ。
錯角の語呂はずばり、
「おまえ、それ、錯覚（さっかく）だZE？」
だ。
えっ。わけがわからない？？
ぜんぜんかっこよくないし、イケテないだって？？
ノンノン。
これから説明していこう。
まず、
砂漠を歩いているシチュエーションをイメージしてくれ。
友だちと、ね。
恋人がいる中学生はガールフレンドでもボーイフレンドでもいい。
とにかく、２人で砂漠を歩いているんだ。
しかも、チョー暑い。
はっきり言って、水が飲みたい。死ぬほど、ね。
そんなヤバい状況で、
友だちがキミにこう言ったんだ。
「あ、あれオアシスじゃね？」
ってね。
でも、キミの目の前には一面の砂漠が広がるだけ。
360°みわたしてもオアシスなんてありそうにない。
望遠鏡をつかっても、だ。
そこで、枯れっ枯れの友だちにこう言ってやるんだ。
「おまえ、それ、錯覚（さっかく）だZE？」
ってね。
えっ、ぜんぜん錯角と関係ないじゃないかって？？
たしかに、一見、無意味にみえるこの語呂。
じつは、もうちょっと分解してみると、
「おまえ、それ、錯覚（さっかく）だZE？」
↓↓
「錯角はZ」
つまり、
錯角は「Z」の角
っておぼえることができるんだ。
だから、3直線でできた「Z」をさがして、
その「Z」によってできた2つの角が「錯角」ってことさ。
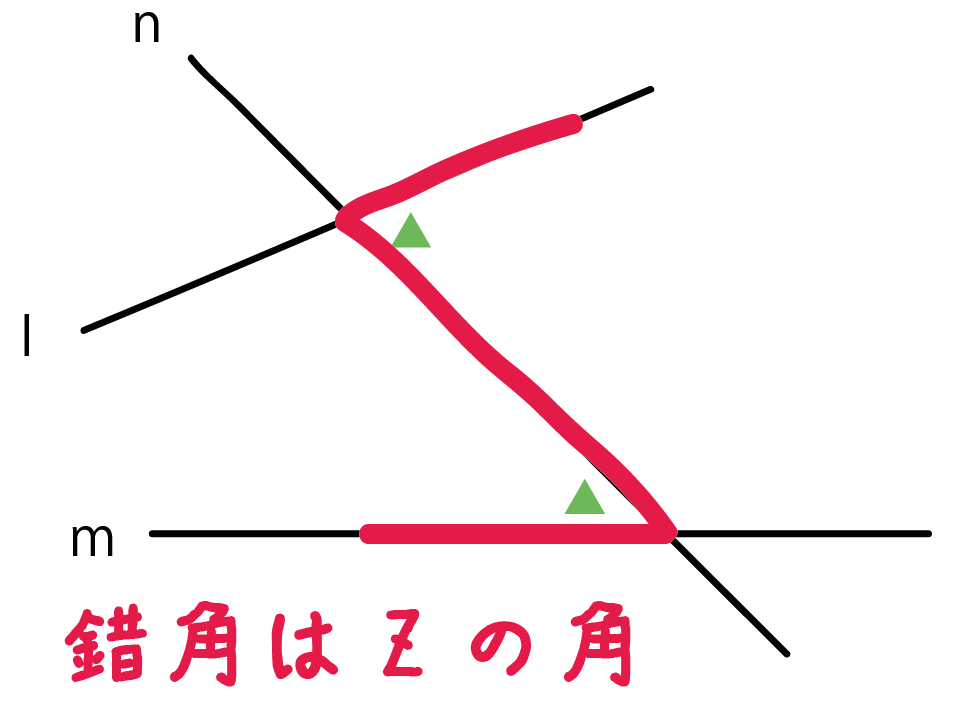
上の図のように「Z」の向きは逆でもいいよ。
錯角をさがせ！
っていわれたら、まずはアルファベットの「Z」をおいてみよう！
同位角と錯角はもうゼッタイ間違えない。
同位角は「イ」を交点におけばいいし、
錯角は「Z」を探せばいい。
あとは問題をときながら慣れていこう！
そんじゃねー
Ken
こんにちは！この記事をかいてるKenだよ。ラーメンは2日に一回でいいね。
対頂角の性質は、
「対頂角は等しい」ってやつだったね。
コイツはむちゃくちゃ便利なんだ。
たとえば、
2直線でできている角度a・bがあったとする。
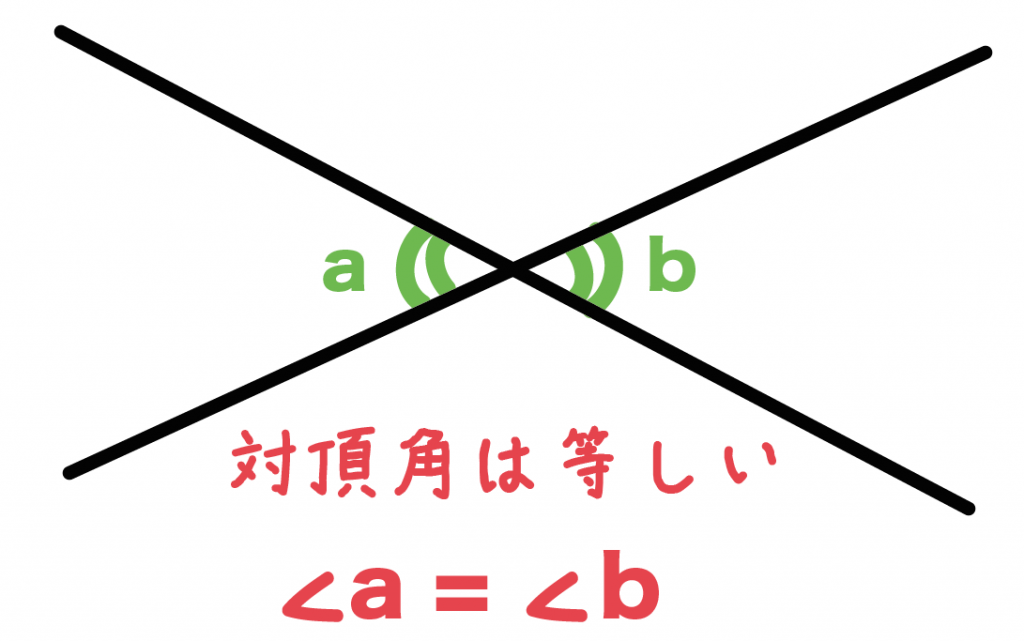
このとき、対頂角のaとbは等しいってわけさ。
今日は、
コイツでガンガン問題をといていこう！
つぎの問題をといてみよう。
例題
下の図のように3直線が1点で交わっています。このとき、角度aの大きさを求めなさい。
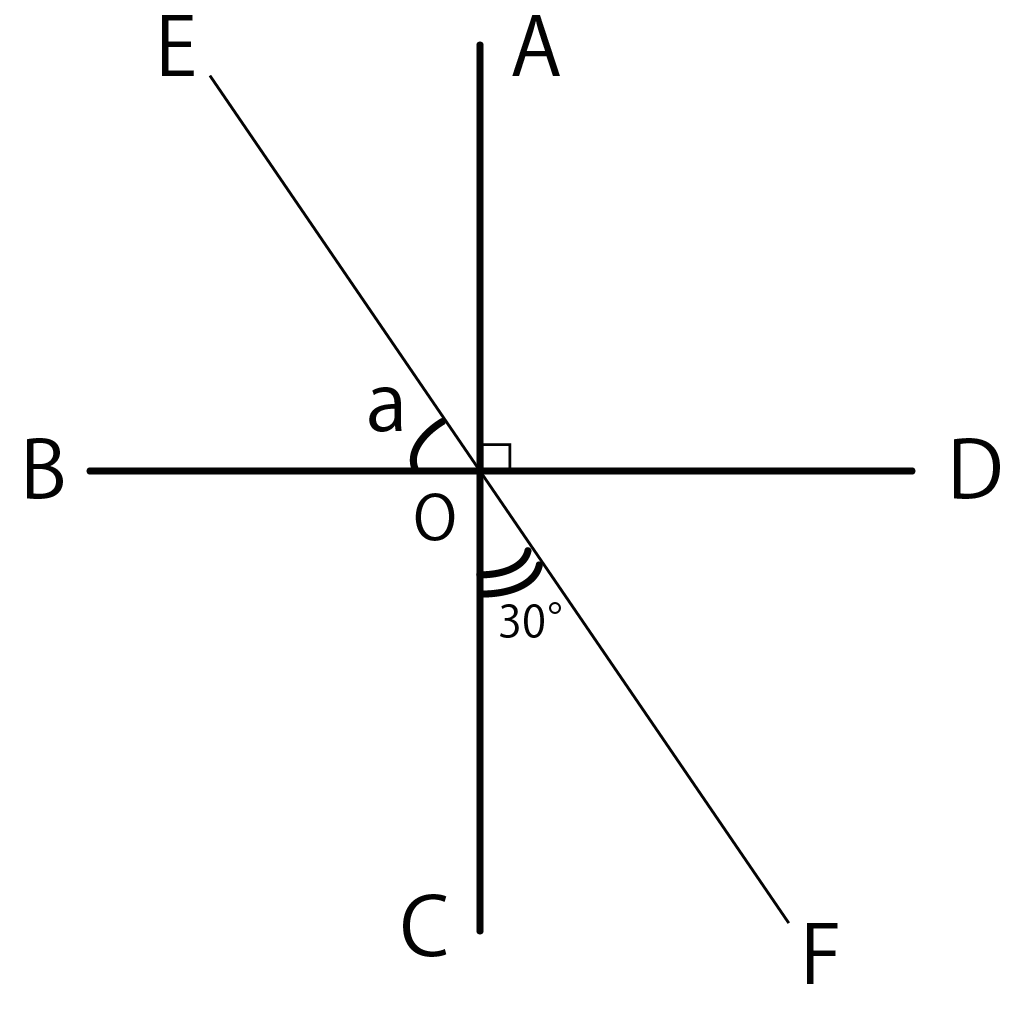
こいつは3ステップでイチコロさ。
さっそくだけど、
対頂角は等しい
という性質をつかっていくよ。
例題で、
「角BOE」と対頂角の関係にあるのは「角DOF」だね？？
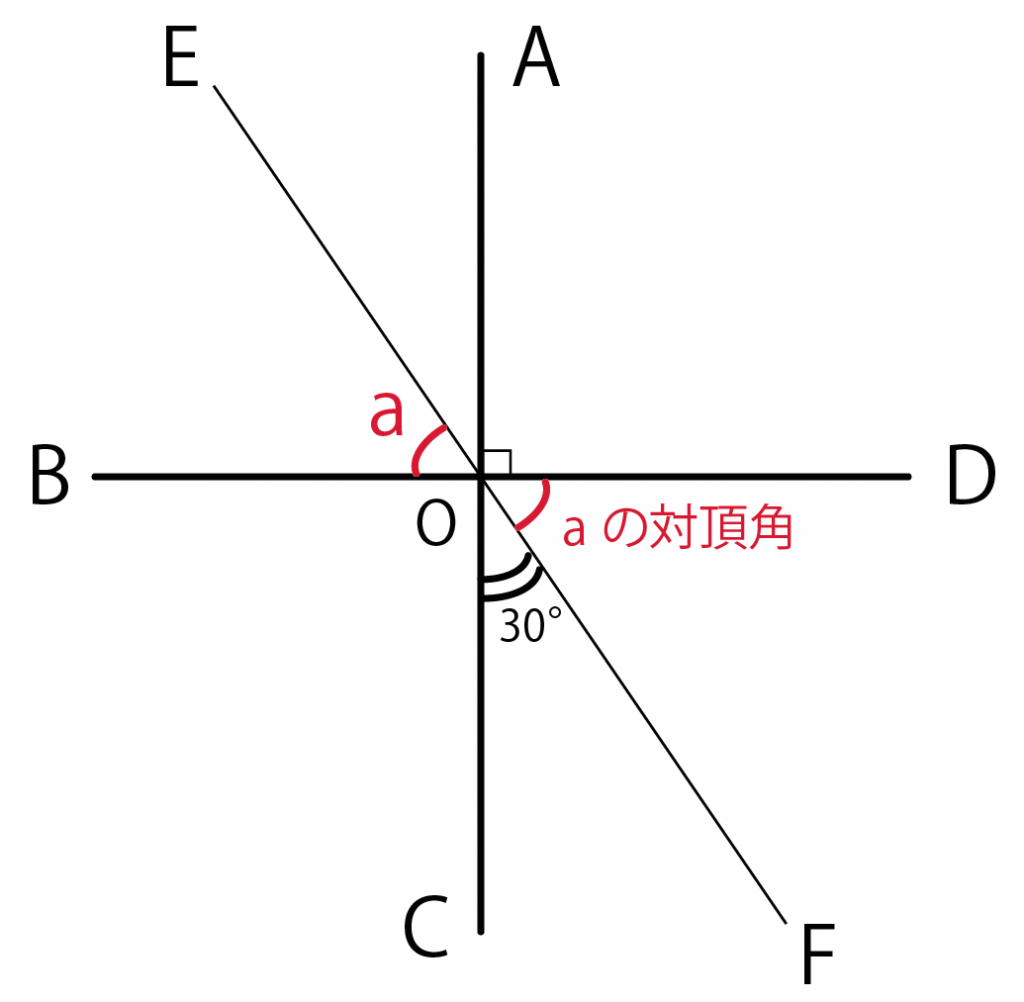
ってことは対頂角の性質をつかうと、
角BOE ＝ 角DOF ＝ a
になる。
対頂角の性質、ナイス。
角度で等式をたててみよう！
例題では、
線分ACとBDは垂直に交わってるから、
角CODは90°。
よーくみてみると、
角COFと角DOF（aの対頂角）を足して90°になってるね。
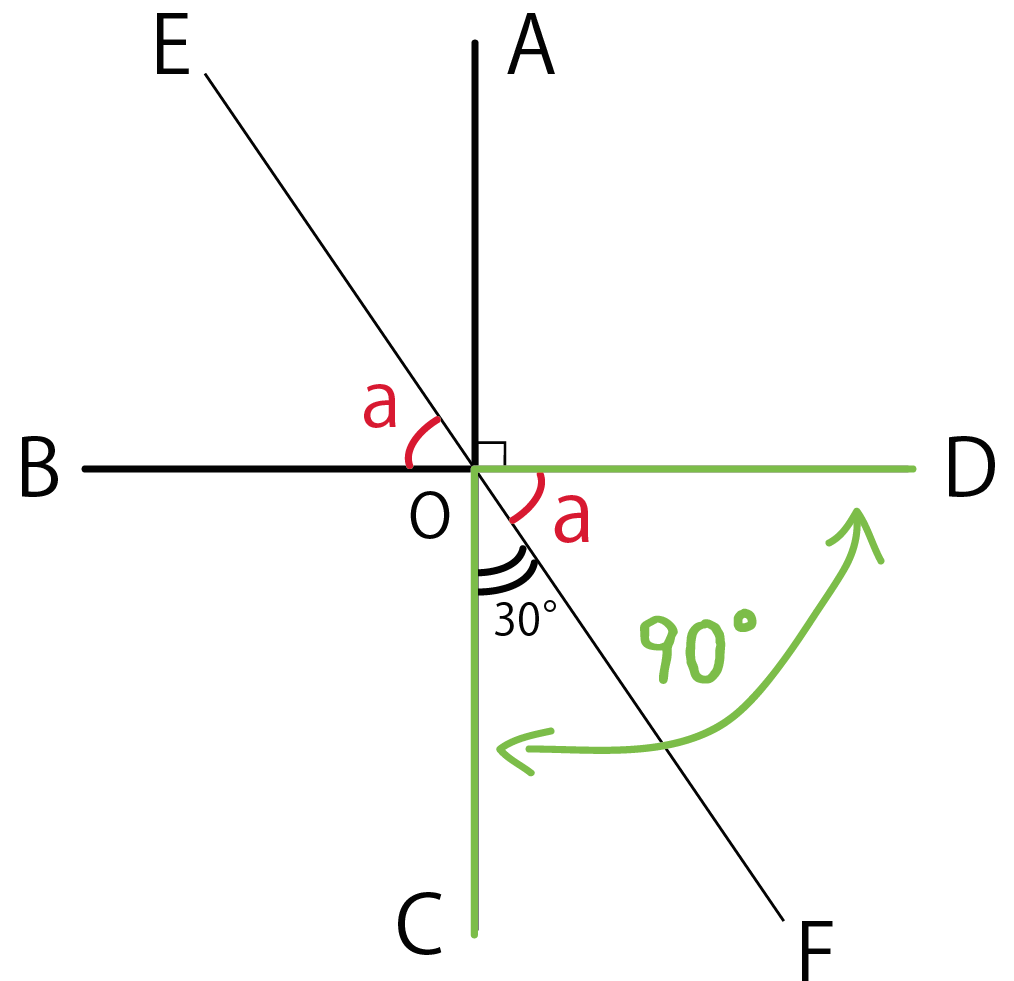
これを式になおしてやると、
角COF ＋ 角DOF ＝ 90°
という等式ができる。
角COF ＝ 30°、 角DOF ＝ a だから、
30° + a = 90°
になるね！
あとは等式を根性でとくだけ。
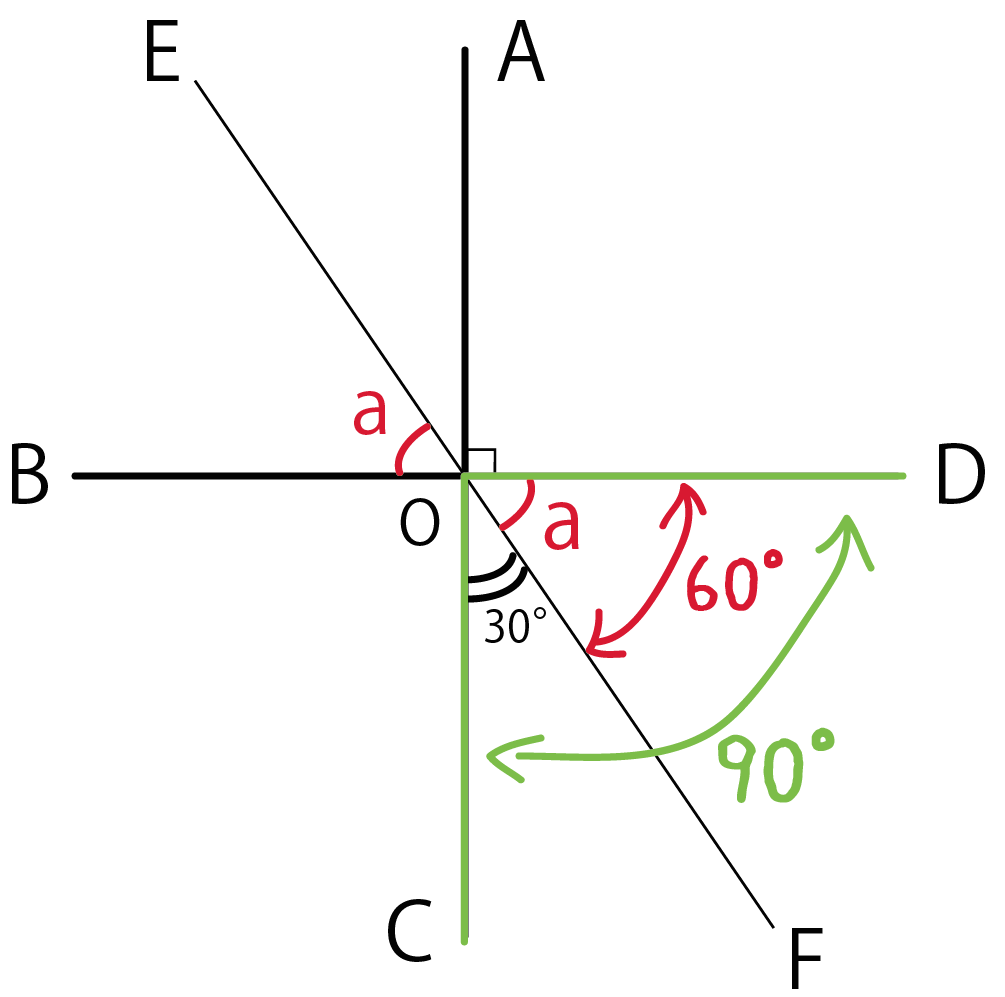
さっきの、
30° ＋ a° ＝ 90°
をaについてとくと、
a ＝ 60°
になるよ！
つまり、
対頂角の性質をつかうと角DOF = aで、こいつに角COF（30°）をたすと、
90°の直角になるから、aは60°になるよ！
ってことさ。
どう？スッキリした？？
対頂角は便利でシンプル。
だからこそ、
もったいぶらないでじゃんじゃん使っていこう。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。チャーシューは2つまでだね。
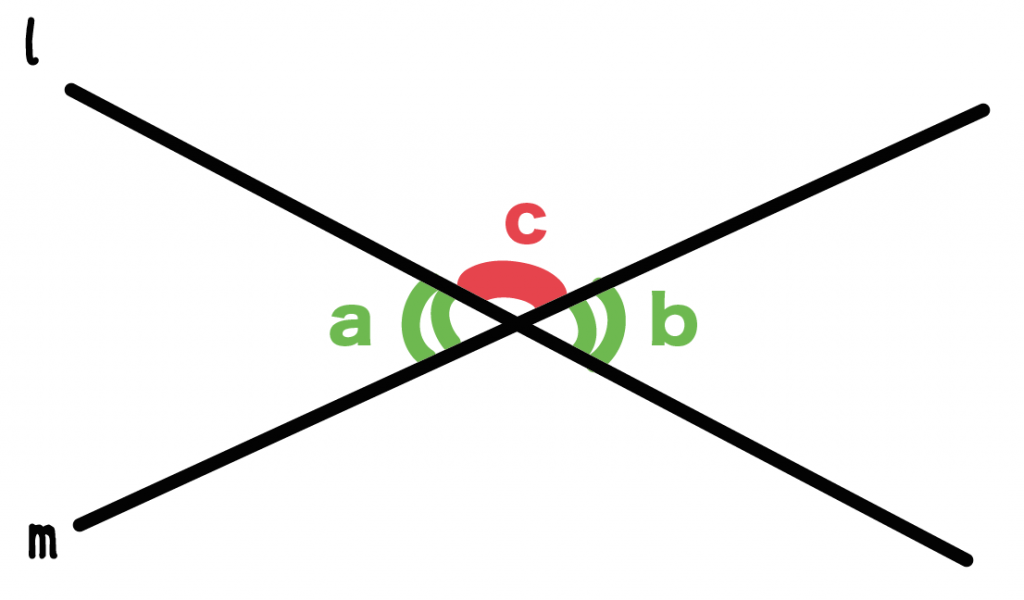
対頂角（たいちょうかく）って知ってる？？
教科書ではつぎのように書いてあるね。
2つの直線が交わっているとき、交点のまわりに4つの角度ができる。
そのうち、向かい合っている角同士のことを「対頂角」という。
名前だけでもカッコいいけど、
もっとすごいのはその性質。
なんと、
対頂角は等しい
ってことが言えるんだよ。
対頂角の角たちを
とすると、
角 a = 角 b
ってことがいえるんだ。
この性質はむちゃくちゃ便利だけど、
なぜ、対頂角が等しいといえるのか？？
が気になるよね。
今日はコイツをふかぼっていくよ！
コツはたった1つ。
それは、
1つの直線ごとに角度を確認していけばいいんだ。
つぎのように、
直線lとmが交わっていて、
その周りにできる角を図のように
とおいてみよう。
まずは直線mに注目するよ。
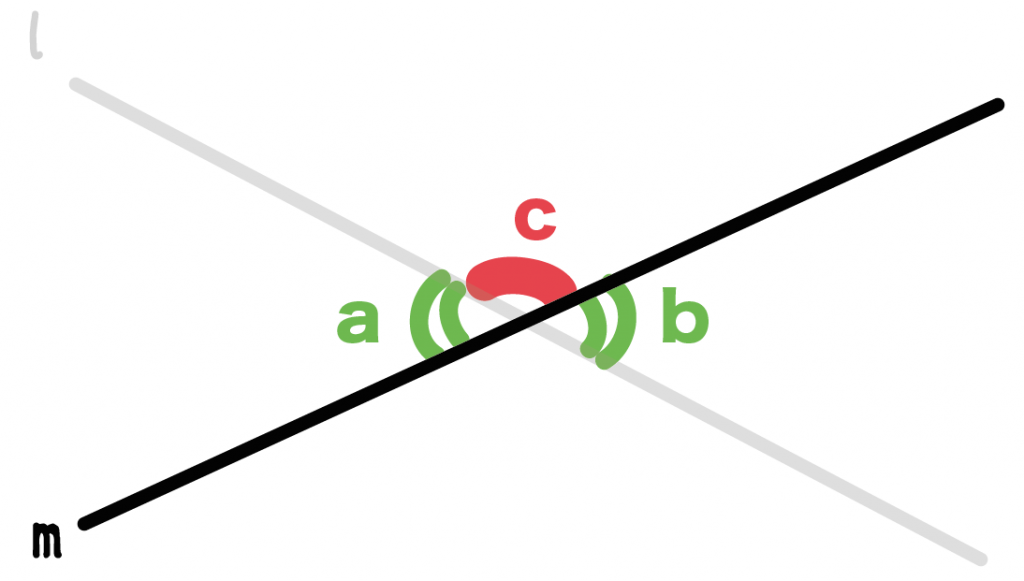
よーくみてみると、
「角a」と「角c」でちょうど1直線になっている
ってことに気づかない？？
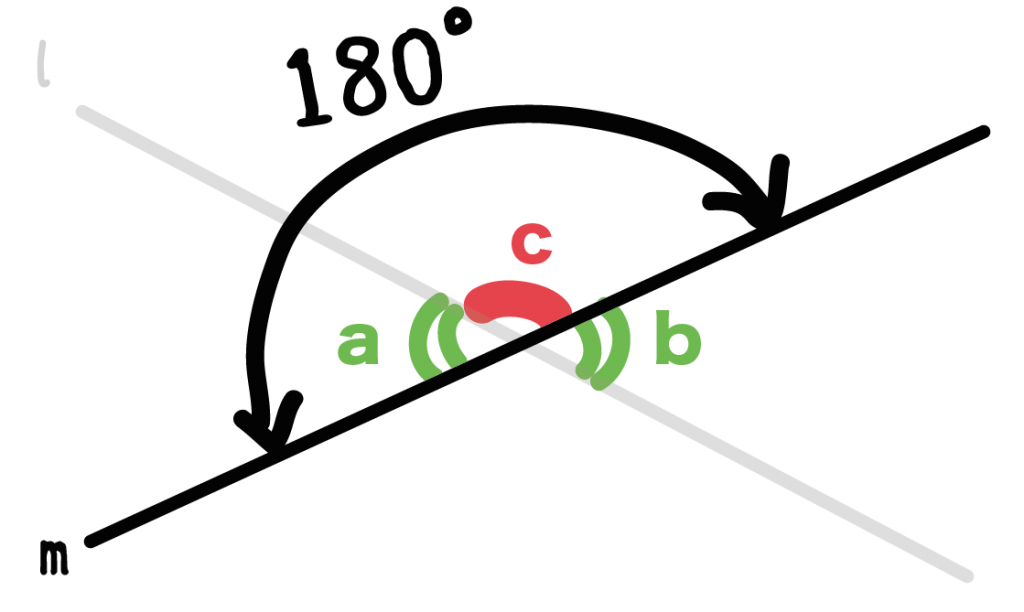
直線の角度は180°だ。
つまり、
角度a + 角度c ＝ 180°
になるね。
等式を変形してやると（角度aについて）、
角度a ＝ 180° – 角度c ・・・・・（1）
になる。この式を(1)としてあげよう。
つぎは直線lだね。
さっきみたいに、
「角b」と「角c」を組み合わせると1直線（l）になってるでしょ？？
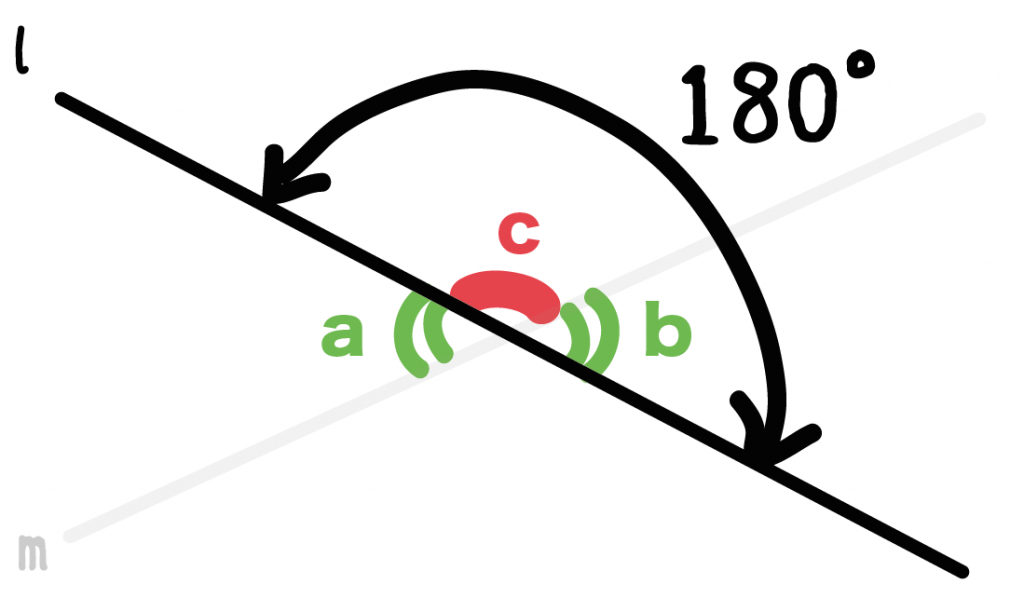
直線の角度は「180°」だから、
角度b + 角度c ＝ 180°
になるね。
等式の変形をしてやると、
角度b ＝ 180° – 角度c ・・・・（2）
になるね。
この等式を（2）としてあげよう。
ここにきて、
の2つの式がでそろった。
（1）と（2）の右辺がまったく同じになってるよね？？
ってことは、
（1）＝（2）
が言えるね。つまり、
「角a」 ＝「角b」
になるね。
角aと角bは対頂角だから、
対頂角は等しい
といえるのさ。
どう？スッキリした？？
対頂角は便利だから今後もガンガンつかってくよ。
だけど、
しっかりとなぜ対頂角が等しいといえるのか？
ってことも忘れずに勉強しておいてね。
そんじゃねー
Ken
