こんにちは!この記事をかいているKenだよ。麻婆豆腐うめえよ。
一次関数で知っておきたいのは、
変化の割合
というキーワードだ。
こんな言葉、滅多に使わないよね??
おれ、変化の割合のこと・・・好き・・・
なんてセリフは出てこないはずだ。
そんなよくわからない、
「変化の割合」
をわかりやすく説明していくよ。
よかったら参考にしてみてね。
一次関数の「変化の割合」とは、
xが1増えたらyがいくら増えるのか、減るのか
の数値のこと。
「yの増加量」を「xの増加量」でわってやれば「変化の割合」になるんだ。
変化の割合 = yの増加量/ xの増加量
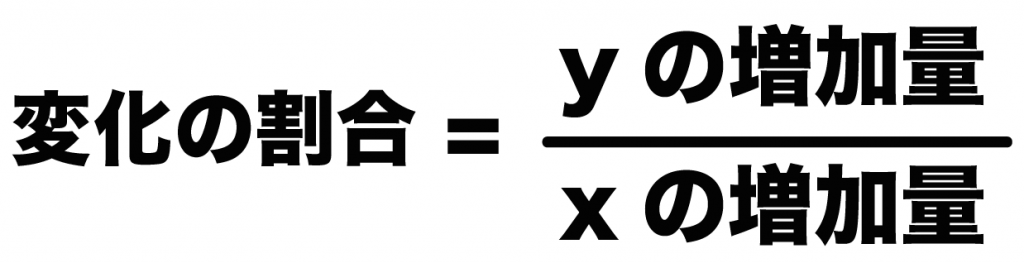
たとえば、
xが2増えたとき、yが10増えたとしよう。
このとき、
だよね。だから変化の割合は、
(yの増加量)÷(xの増加量)
= 10 ÷ 2
= 5
になるね。
つまり、xが1増えたらyが5増える一次関数ってことなのさ。
ここまで大丈夫??
もう一方踏み込んで、
一次関数における変化の割合の特徴
をつかんでおこう。
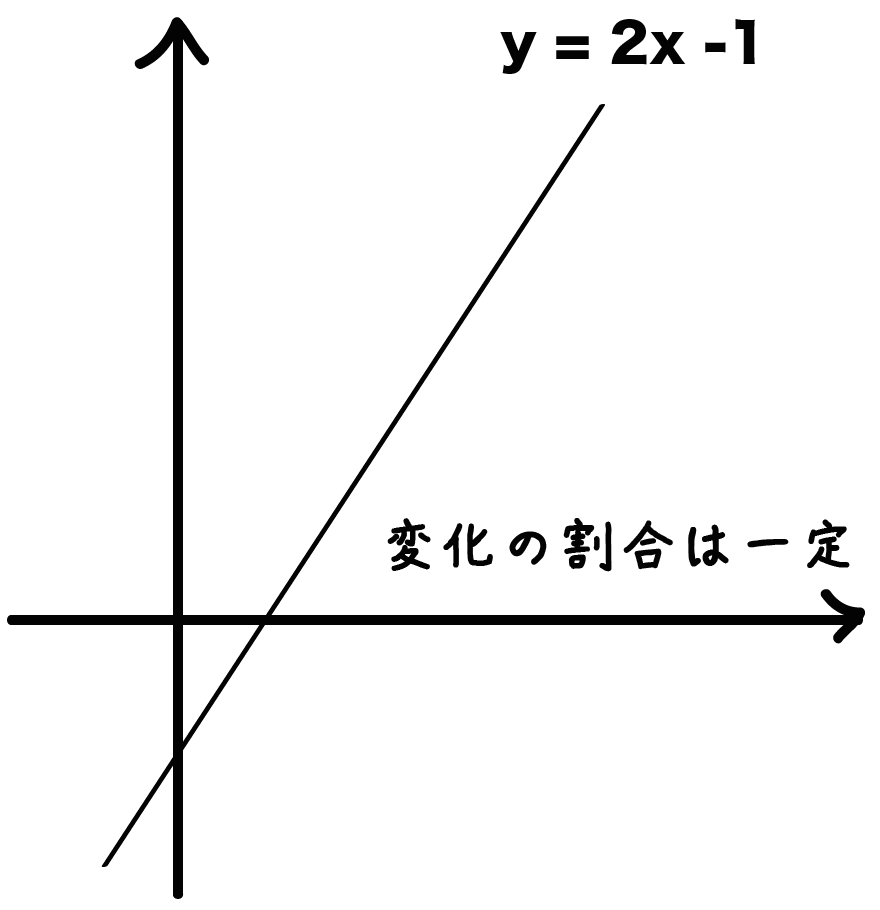
最大の特徴は、
1次関数の変化の割合はずーーーっと一定
ってことなんだ。
つまり、一次関数の途中で「変化の割合」が変わったりしないんだ。
たとえば、
y = 2x +1
という一次関数があったとしよう。
こいつは、
も、変化の割合はずっと2で同じなんだ。
ゼッタイに変わらない。
これが一次関数の変化の割合の特徴さ。
逆に、一次関数でもへったくれでもない関数だったらどうなる??
そう。
変化の割合は一定じゃない。
もうね、コロコロ変わるんだ。
たとえば、つぎのようにクレイジーな関数がいたとしたら、
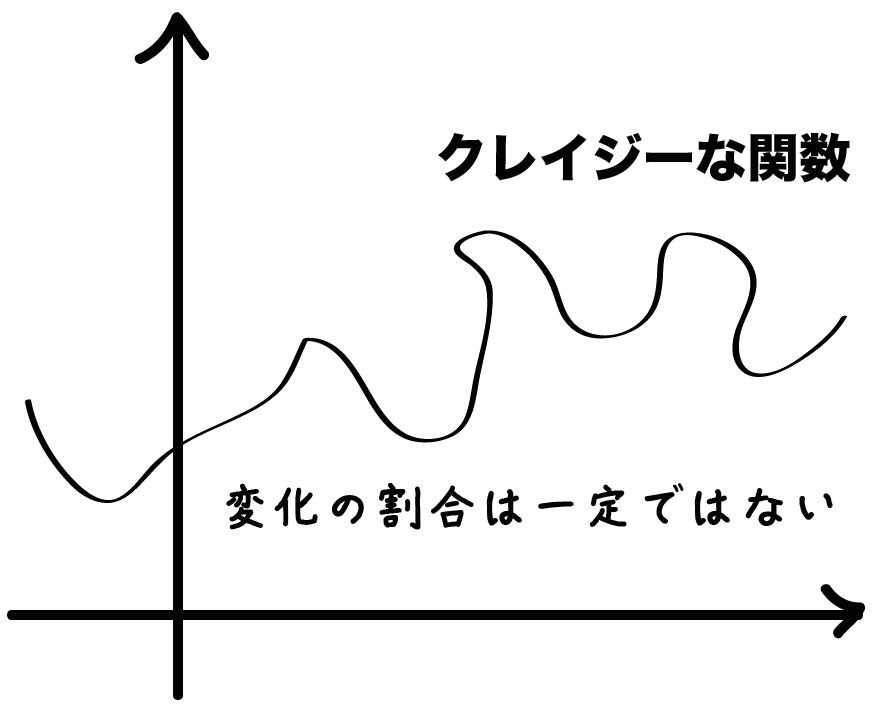
変化の割合はまさに暴れ馬。
xがどの範囲で変化するかによって、ぜんぜん変化の割合がちがうんだ。
一次関数では「変化の割合」が一定である
ってことをおぼえておこう。
一次関数の変化の割合もわかったかな??
コツさえつかめれば問題がとけるようになるから、
ゆっくりと勉強していこうね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。バジル、うめえ。
中学2年生になると、
一次関数
を勉強するね。
うーん、でもそもそも、
一次関数とはなんだろう!??
って思っちゃうよね。
正体不明のまま問題をとくのは無理。
エスパー能力があれば話は別だけどね。

そこで今日は、
一次関数とはなにか??
をわかりやすく説明してくよ。
よかったら参考にしてみてね。
一次関数とは関数の1つ種のことだ。
ポケモンも600匹ぐらいいると思うんだけど、
ピカチュウはそのうちの1匹だよね?
それと同じさ。
「関数とは?」の記事で、
関数とは自動販売機である
ってたとえたよね。
一次関数は自動販売機の一種。
ってことは、アクエリアスしか売ってない自動販売機みたいなもんさ。

ここまではおっけい??
一次関数とはずばり、
y = ax + b
という形をした関数のことさ。

もう少しわかりやすく説明すると、
xが1回以下だけかけられた関数のことなんだ。
yの右側がxの一次式ならそいつは一次関数ってわけさ。
たとえば、
y = 9x
とか、
y = 9000x + 100
が一次関数になるよ。
だって、y = ax + bの形になっているし、xの項はすべて1次式だからね。
これさえ覚えておけば大丈夫。
一次関数を征服したようなもんさ!
ここで勘が鋭いヤツは、
比例は一次関数とどう違うんだよ?!
って逆切れしそうになっているはずだ。
うん、マジ鋭いね。
じつは比例は、
一次関数の1種なんだ。
y = ax + b
のbがゼロになった一次関数が「比例」なんだ。
だんだん「一次関数とはなにか??」ということがわかってきたかな。
つぎの例題をといてみよう↓↓
例題
yはxの関数で、つぎの式で表されるとき、一次関数であるものを選びなさい。
(a) y = 2x
(b) y = 4/x
(c) y = 5x^2+1
(d) y = 1/9x +8
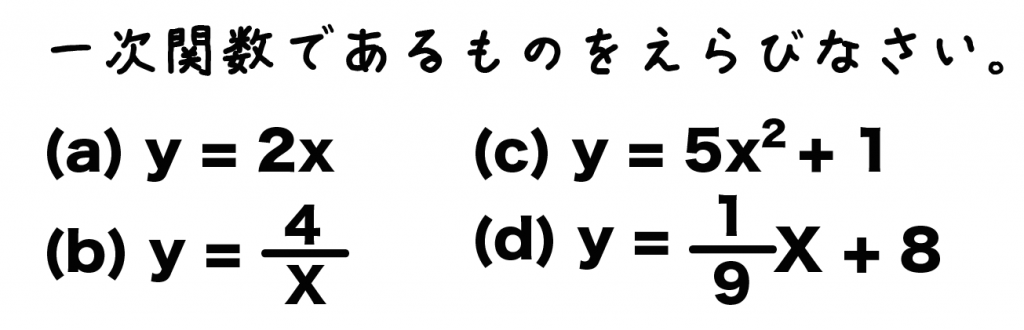
こいつは一次関数だね。
なぜなら、xの次数が1だからね。y = ax + bのbが0のときのパターンさ。
こいつはまぎれもない比例野郎だ。
さっきもいったけど、
比例も1次関数の仲間ってことをおぼえておこう。
こいつは一次関数じゃない。
もうね、とんでもなく違う。
なぜなら、右辺がxで割られているからだ。
xがかけられているなら1次の項になるんだけど、割られているから違う。
xが「かけられてる」のか「わられている」のか把握しておこう。
わからないときは「反比例は一次関数??」っていう記事をよんでみてね。
こいつも一次関数じゃない。
もうね。月とスッポンぐらい違うよ。
なぜなら、
xの項が「二次」だからだよ。
xが2回かけられているところに注意してね。
こいつは一次関数だ。
y = ax + bのaが分数でも一次関数だよ。
aの値にまどわされず、
xが何次の項になっているか??
とか、
y = ax + bの形の関数かどうか??
という判断基準でえらんでね!
一次関数とはなにもの??
ってきかれたらどうする??
そう。
そうだよ。
一次関数とは「xが一次式の関数」だよ!
ってどや顔で答えてやろう。
自信満々で言えばみんな信じてくれるはずさ。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。コーヒーに牛乳は必須だね。
反比例は一次関数なのか?!?
って思うよね。
教科書には詳しくかいてないし、
ちょっともやもやしてない??

今日はその疑問を解消すべく、
反比例の関数は一次関数にふくまれるのか?
をわかりやすく解説してくよ。
よかったら参考にしてみて。
結論からいっちまおう。
反比例は一次関数じゃないんだ。
もうね、ぜんぜん違う。
りんごとみかんぐらい違うね。

えっ。
なんで反比例が一次関数じゃないのかって?!?
そうだね。
これから詳しく解説していくよ。
まずは一次関数とはなにか??
を復習してみよう。
教科書にはこうかいてある↓↓
yがxの一次式で表されるとき、yはxの一次関数である、といいます
だ。
つまり、
関数のxが「一次式」なら一次関数ってことになる。
たとえば、
y = 2x とか y = 5x + 90とかだね。
逆に、y = 2x^2とかy = 5x^3 + 90とかなると、一次関数じゃないってことになる。
だって、xが一次の項じゃないからね。

ここまでオッケイ??
さっそく本題に入ろう。
それじゃあ、反比例の式はどうなのか。
反比例の式って、
y = a/x
だったよね。xが分母にあるタイプの関数だ。
たとえば、
y = 2/x とか y = 6/xとか。

一見、xは何乗もされていない。
ぶっちゃけ、ただのxにみえるから、
こいつも一次関数じゃん!?
って思うかもしれないけど、そいつは間違いだ。
「一次」って、xを1回だけかけたっていう意味なんだ。
でも、反比例の場合、分母にxがあるから、
xで割っていることになる。
よって、反比例は一次関数じゃないんだよ。
xがかけ算されているのか?
割り算されているのか?
をしっかり見極めるようにしよう。
反比例の式は一次関数じゃない。
これを覚えるだけで大丈夫。
一次関数は慣れれば簡単だから、テストでも点をとっていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。水、うまいね。
連立方程式の文章題ってヤッカイだよね。
うん。
むちゃくちゃわるよ、その気持ち。
だけど、もっとメンドクサイ問題があるんだ。
それは、
連立方程式の食塩水の文章題
だ。
ただの食塩水でも難しいのに、それが連立方程式の文章題になる!?
もう、たまったもんじゃない。
こんな問題ときたくないよね?。

今日はそんなラスボスを倒すために、
連立方程式で食塩水の問題を解く方法
を3つのステップで紹介していくよ。
よかったら参考にしてみてね。
つぎの例題をといていこう!
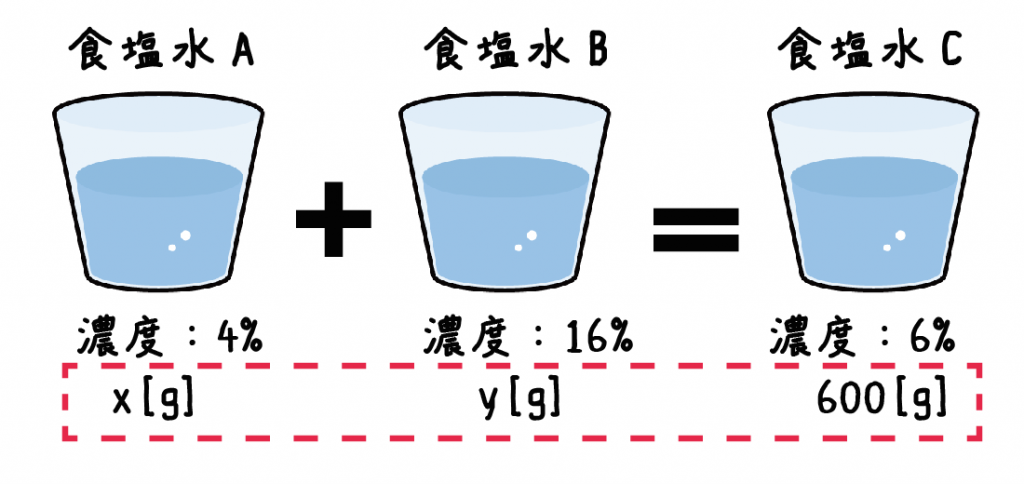
濃度がそれぞれ4%、16%の2種類の食塩水があります。こいつらを混ぜて、濃度が6%の食塩水を600gつくろうとたくらんでます。それぞれの食塩水は何gずつ混ぜたらいいでしょうか??

3ステップで問題を攻略できちゃうよ!
「求めろ!」っていわれてる値を文字でおこう。
これは連立方程式の文章題においても定石だったね。
こっから文章題との闘いがはじまるんだ。
例題をよーくみてみると、
濃度がそれぞれ4%、16%の2種類の食塩水があります。こいつらを混ぜ合わせて、濃度が6%の食塩水を600gつくろうとたくらんでます。それぞれの食塩水は何gずつ混ぜたらいいでしょうか??
って文章の最後の赤い部分に「求めるべき値」がかいてあるよね。
つまり、この文章では、
の2つの値を求めてね!っていってるんだ。
こいつらをx・yとすると、
になるね。
求める値がわからん!!
ってときは文末を読んでみて!
〜を求めなさい!
っていうメッセージが隠されているはずさ。
文字と数字で等式をつくってみよう。
食塩水の文章題ではたいてい、
の2つをつくればいいよ。
「食塩水」と「塩」をわけて考えるのがコツさ。
2種類の食塩水をまぜたらこうなったよ??
ってことを等式であらわしてやればいいんだ。
例題でも「食塩水」と「食塩」に関する等式をつくってみよう。
まずは食塩水の重さに注目。
濃度4%の食塩水x[g]と6%の食塩水y[g]くわえたら、
600[g]の食塩水になったんだよね??
これを等式であらわすと、
x + y = 600
になるね。
2種類の食塩水をたしたら600[g]になりましたよー
ってことを言ってるだけさ。
つぎは食塩の重さに注目してみよう。
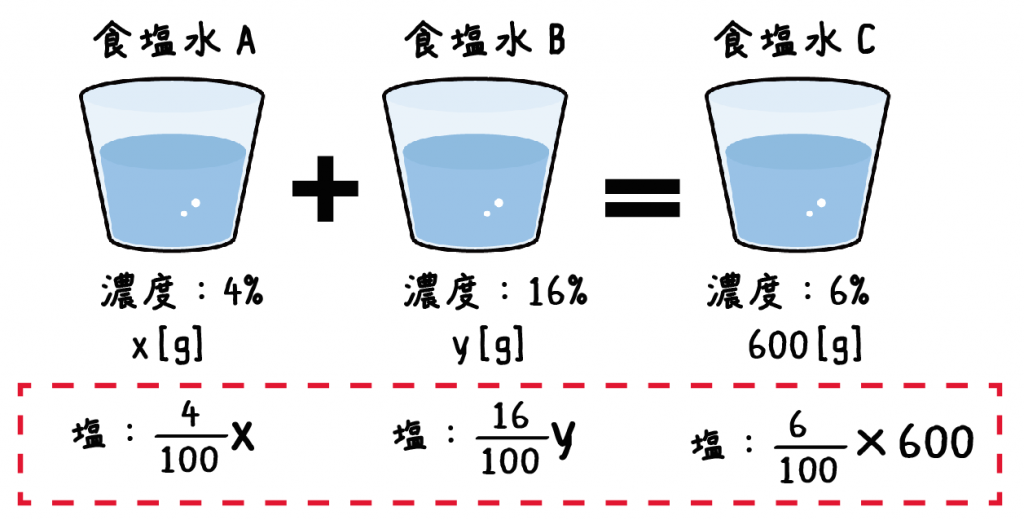
食塩水をまぜても中の「塩の総量」は変わらない。
だから、食塩水の「塩の重さ」だけに注目してやると、
4/100 x + 16/100 y = 6/100 × 600
っていう等式ができるね。
※塩の重さの計算式は食塩水の公式で確認してね。
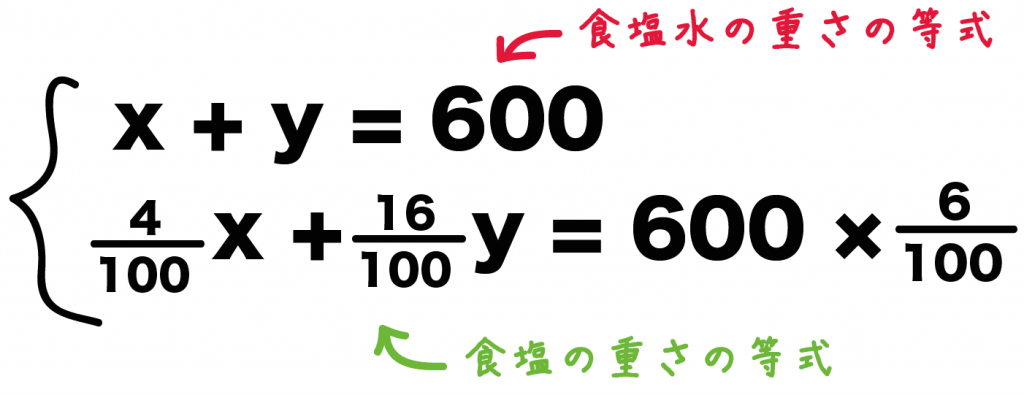
これでやっと、
x + y = 600
4/100 x + 16/100 y = 6/100 × 600
っていう2つの等式がそろった。
文字はxとyの2つだから、連立方程式をとけば答えが求まるよ。
あとは連立方程式をとくだけ。
分数がふくまれる連立方程式の解き方でといてみよう。
「食塩の重さ」の両辺に100をかけてやると、
4x + 16y = 3600
になるね。
これで、
x + y = 600
4x + 16y = 3600
っていうシンプルな連立方程式になった。
加減法でといてあげると、
4x + 4y = 2400
-) 4x + 16y = 3600
—————————-
-12y = -1200
y = 100
って感じでyの解がゲットできるね。
あとはコイツを
x + y = 600
に代入するだけ。
すると、
x + 100 = 600
x = 500
っていう解がゲットできるね。
つまり、
ってわけだ。
おめでとう!食塩水の連立方程式もクリアだね!
連立方程式で食塩水の問題がでても大丈夫。
もうおびえたりしないね。
スムーズに解く最大のコツは、
等式のタテカタにある。
というふうに、
「食塩水の重さ」と「塩の重さ」にフォーカスしよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。グリーンカレー最高だね。
食塩水の問題を攻略したい。
そう思ってない??
ぼくも中学生のときそう思ってたよ。
食塩の重さなんか知らねえよ!?
って問題に逆ギレしてたね、むしろ。

そんなやばいヤツにおすすめしたいのは、
食塩水の公式をおぼえてしまう
っていう裏技だ。
そうすれば、カンタンに解けるようになるから、
食塩水が好きになるはずさ。
今日は「食塩水の公式」を3つにしぼって紹介していくよ。
よかったら参考にしてみてね。
さっそく公式を紹介していくよ。
食塩水の重さを求めよ!
って言われたらつぎの公式をつかってみよう。
「食塩水の重さ」=「食塩の重さ」+「水の重さ」
食塩水の解き方の基本で紹介したけど、
数学でいう食塩水って、
「塩(食塩)」と「水」
しか入ってないんだ。
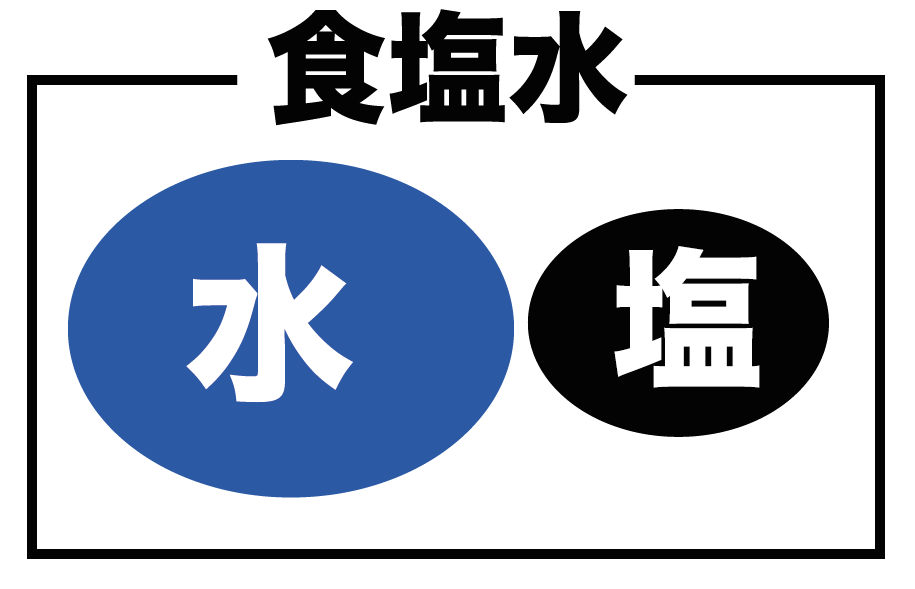
コレ以外には何も入ってないわけ。
ホコリもくそもへったくれもない。
だから、
「食塩水の重さ」は「食塩」と「水」の重さの和ってことになるんだ。
たとえば、
塩8[g]と水道水100[g]をまぜたとしよう。
こいつらを混ぜてできた食塩水の重さは、
8 + 100
= 108[g]
になるんだ。
「食塩水の重さ」の計算は基本中の基本。
しっかりおぼえておこう!
つぎは食塩水の濃度の公式だよ。
濃度 [%] = 食塩の重さ[g] ÷ 食塩水の重さ[g] × 100

食塩水の濃度って、
食塩水にふくまれる「塩の重さ」の割合のこと
だったよね?
だから、濃度を計算するためには、
「塩の重さ」を「食塩水の重さ」で割ってやればいいのさ。
しかも、濃度は百分率(%)で表したいから
最後に100をかければいいんだ。
たとえば、
塩を10[g]と水を200[g]をまぜたときのことを想像してみよう。
さっきの公式の、
濃度 [%] = 食塩の重さ[g] ÷ 食塩水の重さ[g] × 100
に数字をいれて計算してみて。
すると、
濃度[%] = 10 ÷ ( 10 + 200 ) × 100
= 4.76 [%]
になるネ!
文章題で活躍するのが、
食塩水の「塩の重さ」を計算する公式だ。
塩の重さ[g] = 濃度[%] / 100 × 食塩水の重さ[g]

たとえば、
濃度8[%]の食塩水200[g]に塩が何g 入っているか考えてみよう。

こういうときも、
塩の重さ[g] = 濃度[%] / 100 × 食塩水の重さ[g]
っていう公式をつかえば大丈夫。
塩の重さ[g] = 8 /100 × 200
= 16[g]
になるね。
ぜひとも覚えておこう!
食塩水の問題はぶっちゃけ、
公式さえおぼえてればなんとかなる。
ただ、忘れてほしくないのが、
なぜその公式が使えるのか??
を考えておくことだ。
暗記ばかりしても忘れちゃうからね。
テスト前にもう一度確認してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。バームクーヘンっておいしいね。
食塩水の文章問題が苦手な子って多いよね。
何を隠そう。
ぼくも中学生の頃、チョー苦手だったよ。
なぜ食塩水を勉強しなきゃいけないんだ!?
って感じだったね。
ただ、苦手なヤツが多いからか、
テストにむちゃくちゃ出やすい問題になっているんだ。

今日は食塩水の問題の基礎を3つ紹介していくよ。
これで解き方がわかるはずさ。
よかったら参考にしてみてね。
食塩水の問題ってむずかしそうだよね??
でも、3つの基本さえ押さえれば大丈夫。
さっそく紹介していくよ。
まずは基本中の基本。
食塩水ってなんだろう??
ということを復習しよう。食塩水とはカンタンにいってしまえば、
塩がはいった水
のことさ。
「塩」と「ペットボトルの水(エビアンなど)」を買えばすぐに作れちゃうんだ。
それこそ、コンビニでも間に合っちゃうね。
ただ、数学の問題で注意すべきは、
ほんとうに「塩」と「水」以外は入っていない
ってことさ。
ほんものの食塩水にはホコリとか、塩に混じっていた砂糖とか、油汚れとかいろいろ入ってる。
ぶっちゃけ、汚い。
だけど、数学の食塩水は超ピュアなんだ。
もうね、純度100%。

食塩水には「塩」と「水」以外はふくまれていないことを覚えておこう。
食塩水の問題で、
濃度
ってでてくるよね。
これは、
「食塩水の重さ」に対する「塩の重さ」割合
のことなんだ。式であらわすと、
(塩の重さ)÷(食塩水の重さ)
で求めることができるよ。

濃度をあらわすときにはよく、
百分率(パーセント%)
を使うことが多いよ。
つまり、
食塩水を100[g]としたとき、その中に何gの塩がはいっているか??
を表しているんだ。
たとえば、
濃度8%の食塩水があったとしよう。
もし食塩水が100gだったとき、ふくまれる塩は8gってことになるよ。
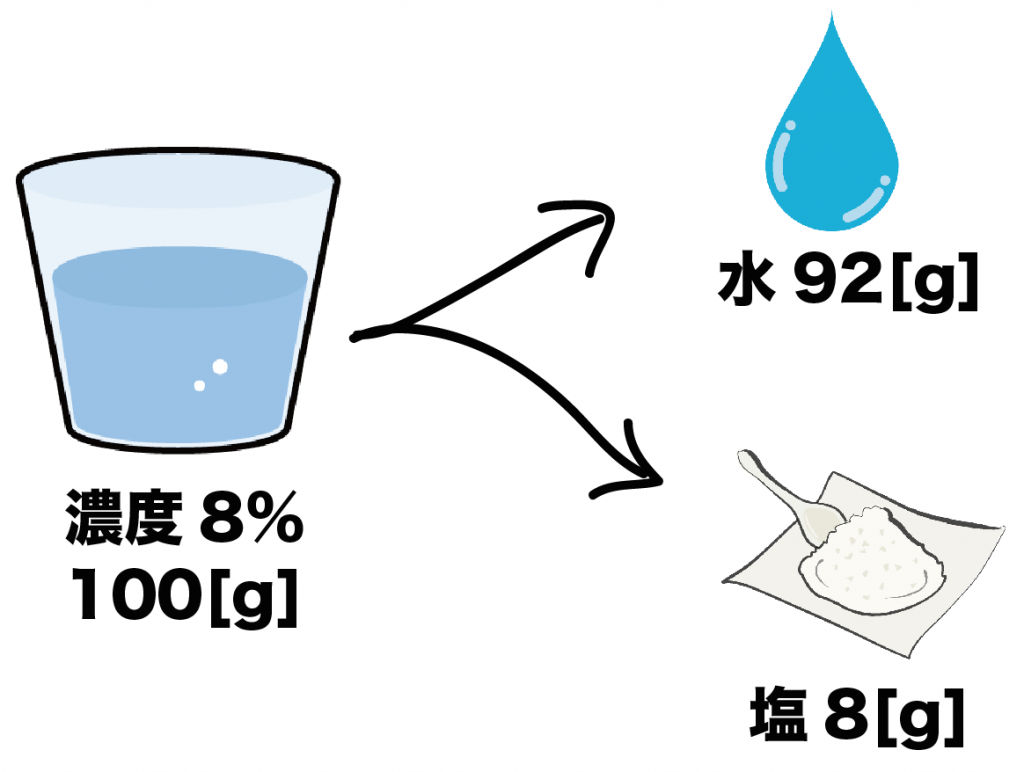
この食塩水が200gあったら塩は16gってことだね!
濃度は「食塩水の重さ」に対する「塩の重さ」の割合
ってことをおぼえておこう。
水に塩をいれたらどうなる??
そう、
そうだよ。
うん。
とけちゃうよね??
水にいれる前は「塩」という固形物だったけど、水にいれてスプーンでかき混ぜると、
見た目上、消えちゃうよね?
「食塩水」が「水」
と同じにみえるんだ。

そう、何も入っていない水みたいだ。
だけれども、
塩は水の中に存在し続けているんだ。
見た目はいないけど、塩はいる。
これを覚えておくと、
食塩水をたしあわせたり、コップをなぐったりしても、
食塩水にふくまれる食塩の重さは変わらないことがわかるね。
だから、食塩水と食塩水をまぜると、中の「塩」と「水」が移動するだけ。
食塩水の問題では見た目よりも、
食塩水のなかに塩が何g入っているのか??
が大切って覚えておこう。
食塩水の問題の基本はどう??
食塩水と友だちになったでしょ。
ふたをあけてみればカンタンなのに、食塩水問題を避けるヤツが多い。
だからこそ、
逆に言ってしまえばチャンスなんだ。
テストでもグイグイ挑戦してみよう!!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。うなぎ好きだね。
連立方程式の文章題って苦手。
ふつうの計算ならできるんだけどなあ・・・・
って思ってない??
えっ。
なんでわかるのかって??
何を隠そう。
ぼくも中学生のとき、そのうちの1人だったからね。
正直、連立方程式の文章題なんてクソクラエと思ってたよ。

今日は、そんな中学生のために、
連立方程式の文章題の解き方
をわかりやすく解説してみたよ。
よかったら参考にしてみてね。
例題をときながら解き方を勉強していこう!
週刊少年JUMPとコロコロコミックが大好きなA君。
JUMPを4冊、コロコロを1冊買ったときの代金は1500円。
また、JUMPを20冊、コロコロを3冊買ったときは6500円の代金がかかってしまい、お年玉がなくなってしまいまいした。
JUMPとコロコロの1冊あたりの値段を求めなさい。
連立方程式の文章題は3ステップでとけちゃうよ。
文中で「求めろ!」って言われている値を文字でおこう。
連立方程式の文章題では、
「○○と××をもとめよ!」
というように、2つの値をゲットしろ!って言ってることが多い。
それらを「x」と「y」っておいてあげればいいんだ。
例題では最後の一文に、
JUMPとコロコロの1冊あたりの値段を求めなさい。
ってかいてあるでしょ??
つまり、
「JUMP1冊の値段」と「コロコロの1冊の値段」がわかればいいんだ。
こいつらを求めるために、
とおこう!
連立方程式の文章題は「最後の一文」から読んでみてね。
文字2つで連立方程式をつくっちゃおう。
あとは連立方程式の解き方さえわかれば大丈夫。
2つの等しい関係をみつけられるかが勝負だ。
例題をみてみよう。
文章題をよーくみてみると、
JUMPを4冊、コロコロを1冊買ったときの代金は1500円。
っていう一文と、
JUMPを20冊、コロコロを3冊買ったときは6500円の代金がかかってしまい
に2つの等式が隠されているんだ。
っていう等式をたてられる。
JUMP1冊の値段を「x円」、コロコロ1冊の値段を「y円」とすると、
のように連立方程式がたてられるね。
文章をよく読んで等式を2つ作ってみてね。
あとは連立方程式をとくだけさ。
のどっちかで解いてみてね。
例題では「加減法」で解いていくよ。
1つめの式を3倍して、1式から2式をひいてあげると、
12x + 3y = 4500
-) 20x + 3y = 6500
———————–
x = 250
ってなるね!
あとは「x=250」を1つめの方程式「4x + y = 1500」に代入してやると、
4 × 250 + y = 1500
y = 500
って感じでyの解がゲットできる。
つまり、
ってことさ。
おめでとう。
これで連立方程式の文章題もマスターしたね。
連立方程式の文章題の解き方はどうだった??
ぶっちゃけた話、
いちばん始めにおく文字さえ間違えなければ大丈夫。
あとは文章題から連立方程式をたてて、
それをいつも通りに解くだけさ。
そんじゃねー
Ken
こんにちは!
中学2年生の連立方程式では、
の2文字がでてきたね!
でも、たまーに、ごくたまーに。
の3文字がでてくる連立方程式もあるんだ。
今日はそんな問題に対応できるよう、
3つの式の連立方程式(xyz)の解き方
を4ステップで解説していくよ。よかったら参考にしてみて。
解き方のポイントは、
「1つの式」をつかって「1つの文字」を消去する
ということさ。
例題をときながらみていこう。
つぎの連立方程式を解きなさい。
x + y – z = -6 ……(1)
2x + 4y + 3z = 9 ……(2)
5x + 3y +z = 4 ……(3)

1つの式だけで文字を1つ消去してみよう。
えっ。どの文字を選んだらいいのかわからないだって??
そういうときは、
なるべく係数が小さい文字をえらんでみて!
加減法で文字が消しやすいからね。
例題でいうと、
すべての係数が1の
x + y -z = -6
を選んでみよう。
そんで、係数が小さい「z」を消してみよう。
(1)式をつかって「z」を消すために、
という計算をしてみて。加減法をつかっているよ。
すると、
の2つの式に進化するよ!
3つの文字が2つになったでしょ??
もうひと頑張りして、
2つの文字を1つにしてみよう!
例題ではStep1で、
みたいに2つの文字の連立方程式をゲットできたよね。
こいつを加減法で解いてみよう。
「y」を消すために、
(4)式を7倍、(5)式を4倍して両者を引き算してやると、
42x + 28y = -14
-) 20x + 28y = -36
——————–
22x = 22
x =1
になるね!
ゲットした解を式に代入してみよう。
代入して方程式をとけばいいんだ。
例題でいうと、(4)式の
6x +4y =-2
に「x =1」を代入してみよう。
すると、
6 × 1 + 4y = -2
となって、
4y = -8
y = -2
になるでしょ。
これでyの解もゲットできたね!
文字はあと1つだね。
これまでにゲットした2つの解を「xyz」の連立方程式に代入してやろう。
例題では、
っていう2つの解がわかってるよね??
こいつらをxyzの式に代入してやればいいんだ。
(1)式に代入してみると、
x + y -z = -6
1 -2 -z = -6
z = 5
となったね。
おめでとう!
xyzの解である、
(x, y , z) = (1, -2, 5)
が求まったね。
3つの文字がはいっていたらメンドイ・・・・
そう思っちゃうよね?
ただ、実際に使っているのはこれまで勉強してきた、
なんだ。式が3つに増えて慌てちゃうかもしれないけど、冷静に対処してみよう。
「ちょっと加減法と代入法が心配・・・!」
というときはこれを機に「連立方程式の解き方」を復習してみてね。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。回転寿司いいね。
小数の連立方程式ってむずかしいよね??
たとえば次のような問題さ。
例題
つぎの連立方程式を解きなさい。
0.4x + 0.01y = 1
x + y = 22
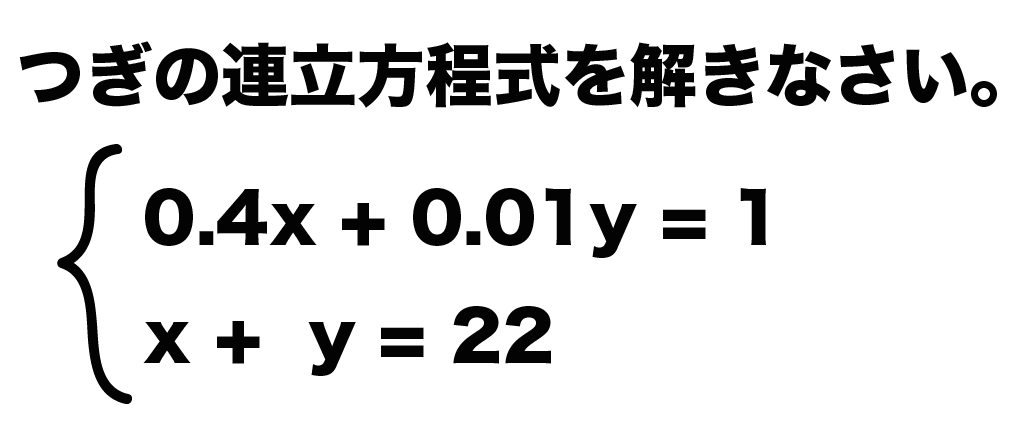
こんな感じで、
どっちかに「小数」がまじっているときは要注意。
こういうときは、連立方程式の解き方でふつうに解く前に、
「あること」
をすればいいんだよ。
今日はそのコツを解説していくねー!よかったら参考にしてみて!
小数の連立方程式は4ステップでとけちゃうよ。
例題を解いてみよう!
例題
つぎの連立方程式を解きなさい。
0.4x + 0.01y = 1
x + y = 22
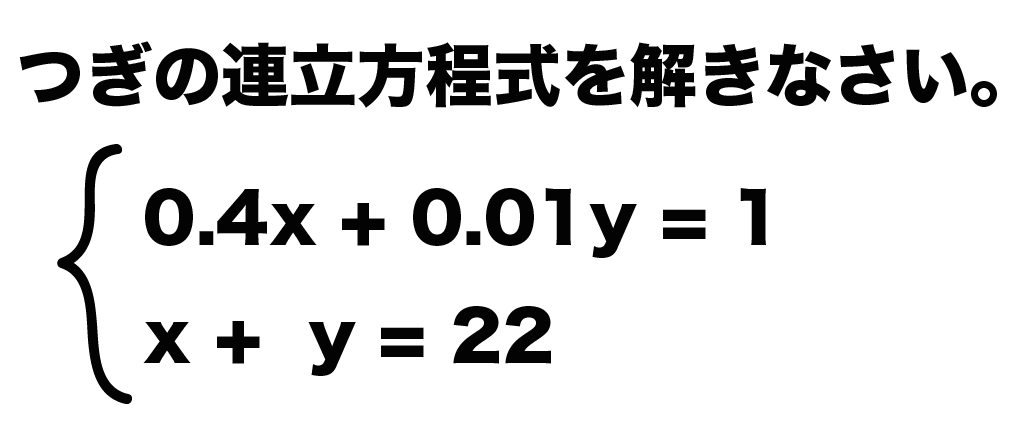
連立方程式から小数を消そう!
小数がなかったらフツーの連立方程式と同じだからね。
えっ。どうやって小数を消せばいいのかって?!?
じつは、
いちばん小さな小数の項が消えるように「ある数」を両辺にかける
だけでいいんだ。
かける数は、
いちばん小さい小数が小数点第何位か??
によって違うよ。
つまり、
小数点のうしろに数字が何個あるか
ってことだね。
のように、かける数をかえていけばいいんだよ。
例題の、
0.4x + 0.01y = 1
をみてみて。
いちばん小さい小数の項は「0.01y」だよね??
これは「.」 の後ろに2つ数字があるから、
小数点第2位の小数だね。
ってことは、100を両辺にかけてやれば小数が消せるのさ。
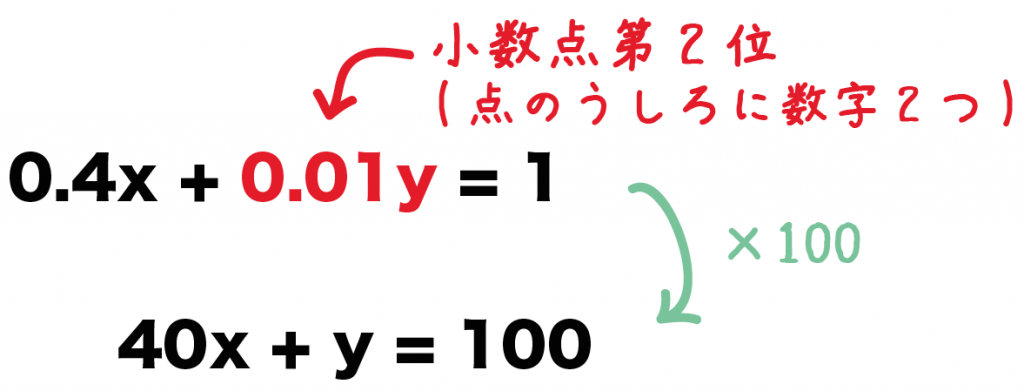
両辺に100をかけてやると、
40x + y = 100
になるね。
これで小数ともおさらば!
小数の次は「文字」を消しちゃおう。
消し方って2つあったよね??
好きな方で文字を消してみてね。
例題をみてみよう。
小数を消したあとの式は、
40x + y = 100
x + y =22
になる。
yの係数が「1」で同じだから加減法で文字を消そう!
1つ目の方程式から2つ目をひいてやると、
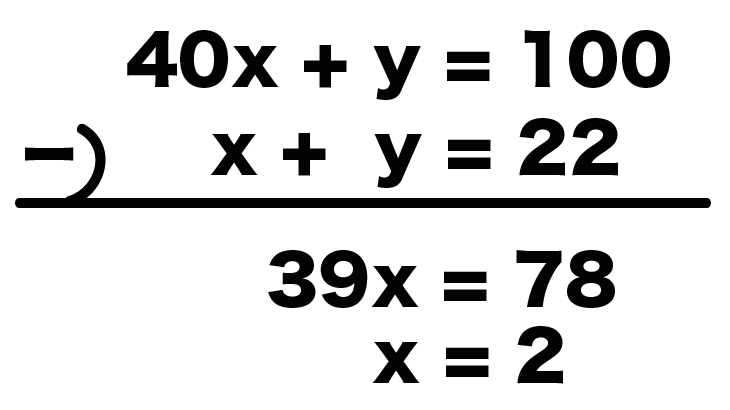
40x + y = 100
– ) x + y =22
——————-
39x = 78
x = 2
になるね!
これでxの解がゲットできた。
あとはyだけだ!
解を式に代入してみよう。
計算が楽なほうを選んでね。
例題では2つ目の式の、
x + y = 22
に解である「x = 2」を代入してみたよ。
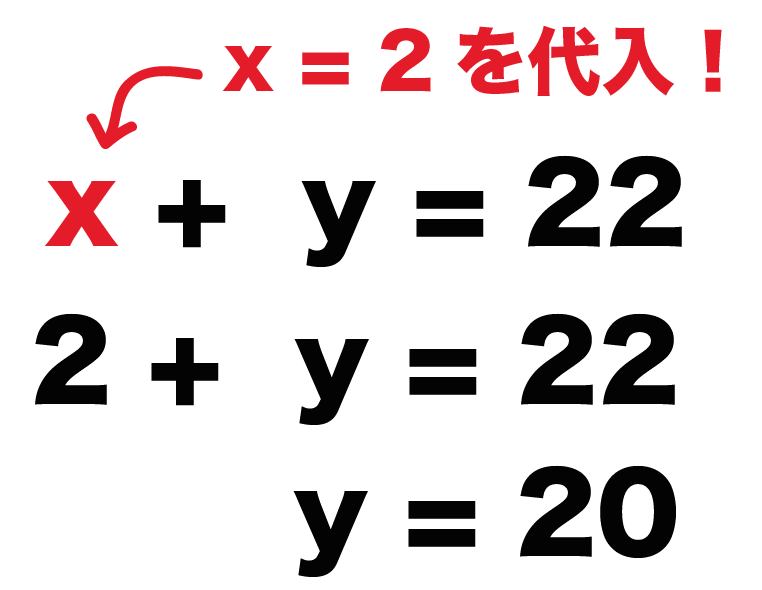
代入して方程式をといてやると、
2 + y = 22
y = 20
になるね!
これでxとyの解のセットである、
(x, y) = (2, 20)
がゲットできたね。
おめでとう!!
小数がはいった連立方程式の解き方はカンタン!
小数を消しちまえばいいんだ。
両辺を10倍、100倍、1000倍とかしてやれば、
とりあえず大丈夫w
小数は消えるからね。
問題を解いてゆっくり慣れていこう!
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。ジムに通い始めたね。
分数がはいっている連立方程式
って、たまにあるよね??
↓ たとえばこんな感じ ↓
例題
つぎの連立方程式を解きなさい。
$$\frac{x}{2} + \frac{y}{4} = 1$$
$$3x + 2y = 5$$

これみたいに、
分数がいるときは要注意!
テストでも間違えやすいところなんだ。
今日は、
分数がふくまれている連立方程式の解き方
をわかりやすく解説していくよ!
つぎの3ステップでとけちゃうよ!
例題をときながらみていこう!
例題
つぎの連立方程式を解きなさい。
$$\frac{x}{2} + \frac{y}{4} = 1$$
$$3x + 2y = 5$$

分数を消しちゃおう!
方程式から分数をなくすには、
分母の最小公倍数を両辺にかければいいんだ!
例題の分母の「2」と「4」の最小公倍数は「4」だね。
$$\frac{x}{2} + \frac{y}{4} = 1$$
に最小公倍数「4」をかければいいんだ。
左だけじゃなくて右にもかけてね!

すると、
$$2x + y = 4$$
になるよ。
ね?
分数がなくなったでしょー?
最小公倍数がわからないときは、
ぜんぶの分母を両辺にかけてやればいいよw
めんどいけど、確実に分母を消せるからね!
これで第一ステップ完了さ!
つぎは「文字」を消去してやろう!
連立方程式から文字を消す方法って、
の2つだったよね。
どっちを使うかわからないときは、
連立方程式の解き方のコツをみてみてね。
分母をはらったあとの連立方程式、
$$2x + y = 4$$
$$3x + 2y = 5$$
は「加減法」を使って解いてくよ!
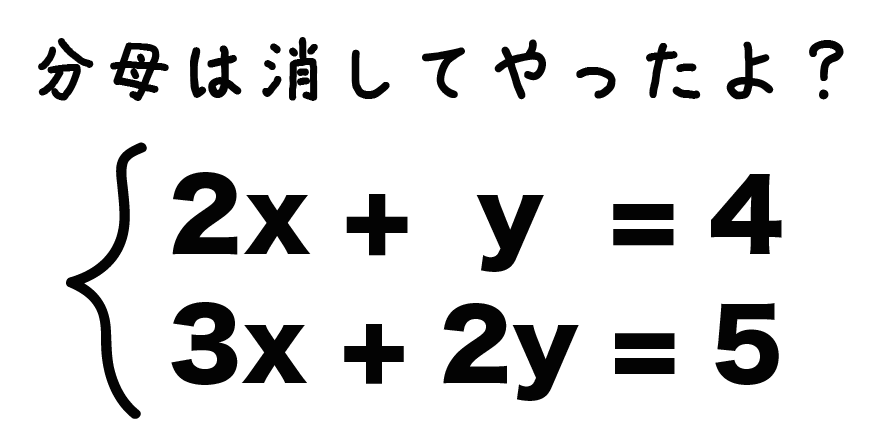
上の式を2倍して、上から式をひいてやると、
4x + 2y = 8
– ) 3x + 2y = 5
——————-
x = 3
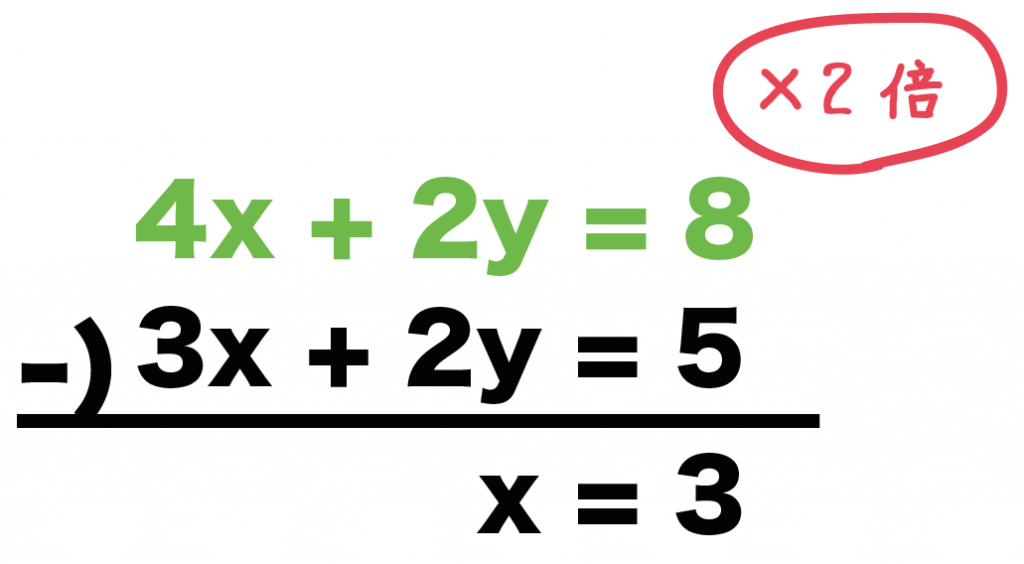
xの解が「3」になるよね!
こんな感じで、
文字を消去して解いていこう!
ゲットした解を代入してみよう。
計算できそうなヤツを選んで代入してくれ。
例題では、
$$3x + 2y = 5$$
に「$x = 3$」を代入してみようか!
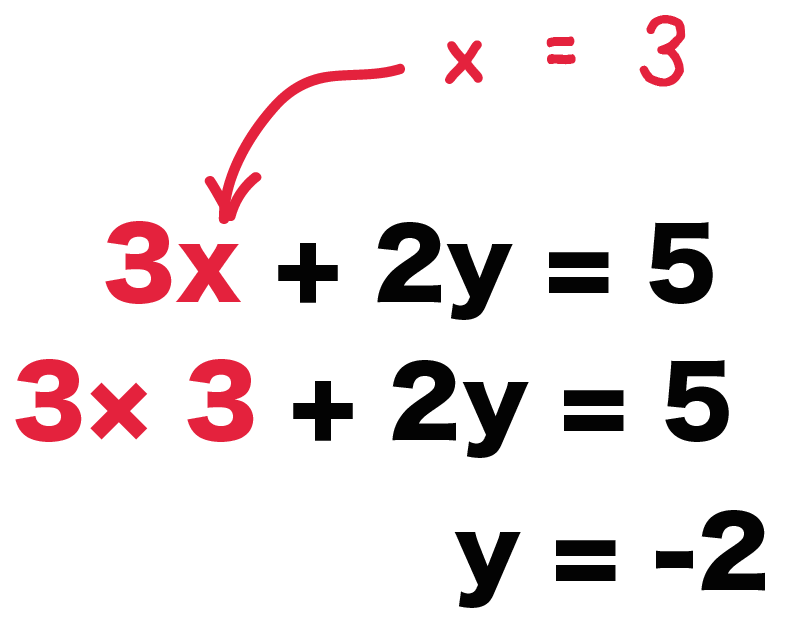
すると、
$$3 × 3 + 2y = 5$$
$$9 + 2y = 5$$
になるよ。
この方程式を中1数学でならった方程式の解き方でといてやると、
$$y = -2$$
になるね!
おめでとう!
これで連立方程式の解である
$$(x, y) = (3, -2)$$
がゲットできたね。
連立方程式に分数があるとむずかしそうだよね??
だけど、
やることは案外すくないよ。
ただ、
分母をはらう
ってことを、最初にすればいいんだ。
慣れるまで問題を繰り返しといてみてね!
連立方程式専門の問題集作ってみたから、よかったら使ってみて。
そんじゃねー!
Ken
連立方程式の加減法はチョー便利。
テストではだいたい「加減法」を使うからね!
「代入法」を使うのは結構だるいんだよ。
「加減法」なら楽できるってわけさ。

今日は、
連立方程式の解き方「加減法」をわかりやすく解説していくよ。
よかったら参考にしてみてね。
つぎの例題をときながらみていこう!

加減法なら4ステップで解けちゃうよ。
文字の係数をそろえちゃおう!
文字の項のうち、1つでも係数が一緒ならいいんだ。
例題の連立方程式をみてみると、
x・yの係数は一緒じゃない
ことがわかるよね?

たとえば上のxの係数は「2」だし、
下の$x$の係数は「3」だからね。ぜんぜん同じじゃない!
これは$y$だって同じことさ。
こういうときは、
それぞれの方程式に「ある数」をかけて係数をそろえるんだよ。
等式の性質のうち、
同じ数を両辺にかけても等式は維持される
ということを使ってやろう。
たとえば上の
$$2x + 5y = 12$$
の両辺に「3」をかけてやると、
$$6x + 15y = 36$$
になるよね?
これと同じように下の
$$3x – 7y = – 11$$
に「2」を両辺にかけてやると、
$$6x – 14y = -22$$
になる。
どっちの方程式でも「xの係数」が「6」になったね。
文字の係数が同じになった??
今度はその文字を消しちゃおう!
消し方は、
2つの方程式を「足し算」するか?
それとも「引き算」するか?
の2パターンさ。
消したい文字の符号が同じならば「引き算」。
符号が違うなら「足し算」すればいいんだよ。
例題ではxの係数は「6」で同じで、
さらに符号も「+」だから一緒だね。

2つの方程式を「引き算」すればいいんだ ↓↓
引き算してやると、xが消されて、
$$29y = 58$$
になるね。
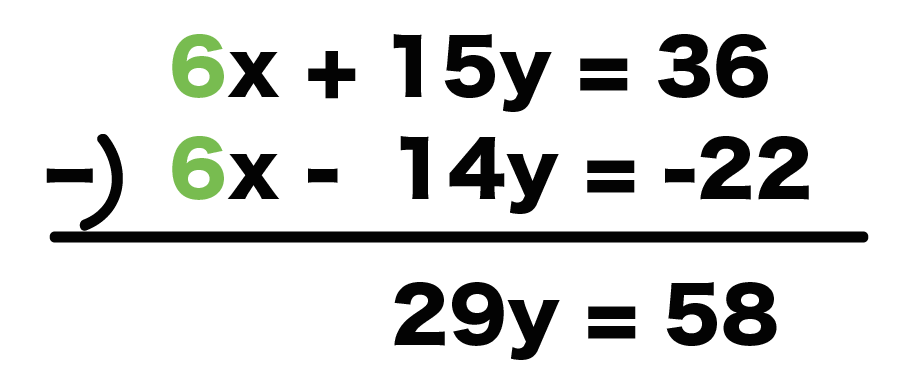
文字が一つになった??
文字が1つの方程式の解き方って中1数学でならったよね??
勉強したことを使ってやればいいんだよ。
例題でいうと、
$$29y = 58$$
の両辺をyの係数「29」わってみよう。
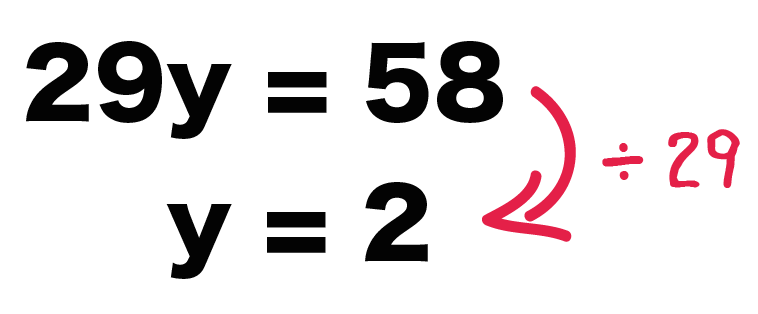
すると、
$$y = 2$$
っていう解がゲットできたね!
あとはxだけだ!
解を方程式に代入してみよう!
代入して方程式をとけばいいのさ。
例題の「$y = 2$」っていう解を
$$2x + 5y = 12$$
に代入してみよう。
すると、
$$2x + 5 × 2 = 12$$
になるね。
この方程式をとくと、
$$2x + 10 = 12$$
$$2x = 2$$
$$x = 1$$
になるね。これがxの解さ。
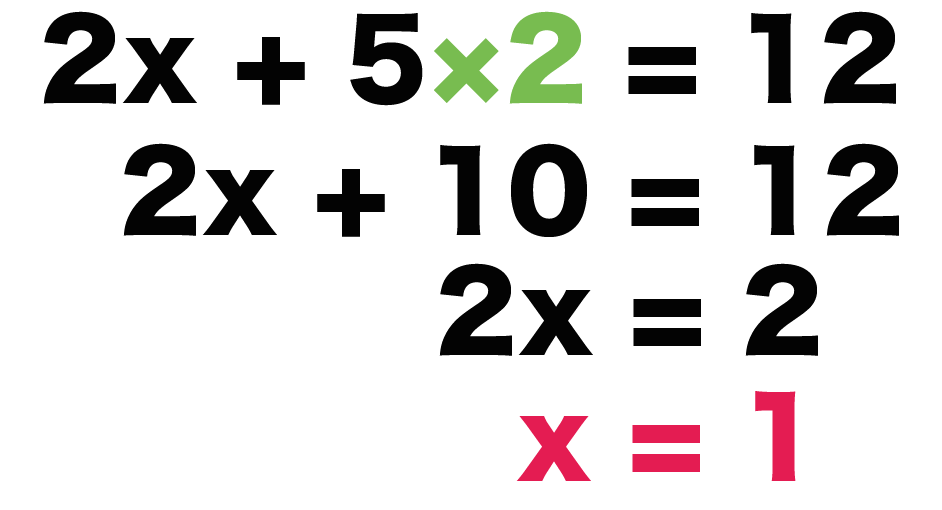
おめでとう!
これで連立方程式の解の
$$(x, y ) = (1, 2)$$
が得られたね。
連立方程式の加減法はよく使うよ。
だからこそ、
時間がかかってもいい。
間違えずに解けるようにしたいね。
っていう4ステップだけさ。
身に付くまで繰り返し問題を解いてみよう!
そんじゃねー
こんにちは!この記事をかいているKenだよ。肉じゃがはウマいね。
連立方程式には解き方が2つある。
だったよね??
連立方程式の解き方でも紹介したけど、
迷ったら「加減法」をつかったほうがいいよ!
だって、簡単だからね。
だけど、
ごくたまーに、
代入法が活躍するときもあるんだ。

今日は、そんなときにそなえて、
連立方程式の代入法の解き方を解説していくよ。
よかったら参考にしてみてね。
例題といっしょに解説していくよ。
例題
つぎの連立方程式を代入法で解きなさい。
2x +3y = 14
3x + y = 0

代入法はつぎの4ステップでいいんだ。
どっちの式でもいい。
「係数1」の文字を左辺によせて、ソレ以外を右辺におしやろう。
係数1ってつまり、文字に何も数字がついていないってこと。
たとえば、
yとかxとかaとかね!
そうすることで、
係数1の文字 = ソレ以外
という等式に変形できちゃうんだ。
例題では、
「3x + y = 0」で「文字= ソレ以外」をつくってみよう。
「-3x」を右辺に移項してやると、
y = -3x
に変形できるね。

これで準備完了。
寄せた式をもう一方の式に代入してあげよう。
そうすることで、
方程式から文字を1つ消せるんだ。
例題でいうと、
「y = -3x」を「2x + 3y =14」に代入すればいいよ。
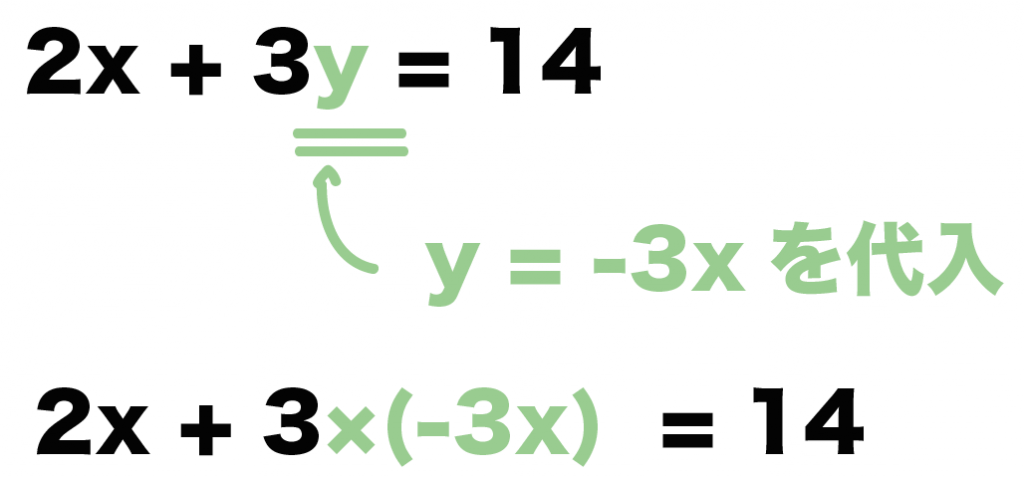
すると、
2x + 3 × ( -3x) = 14
になるね。
代入後の方程式を実際にといてみよう!
解き方がわからんときは「一次方程式の解き方」を参考にしてね。
例題で代入した方程式を簡単にしてやると、
2x + 3 × (-3x) =14
-7x = 14
になるよね?
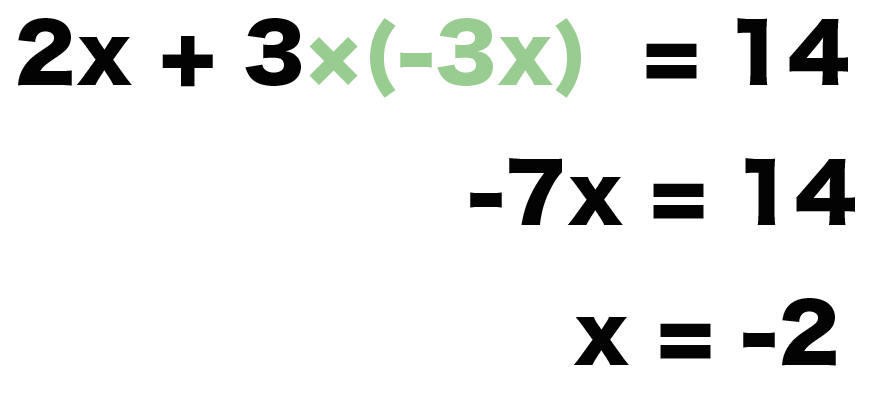
両辺をxの係数7でわってやると、
x = -2
になるよ!
この解を方程式に代入してあげよう。
代入する方程式はどっちでもいいよ。好きな方を選んじゃってくだせえ!
例題でいうと、xの解は「-2」だったよね??
これを「y = -3x」にいれてみよう。
すると、
y = -3 × (-2)
= 6
という解がでてくるでしょ??
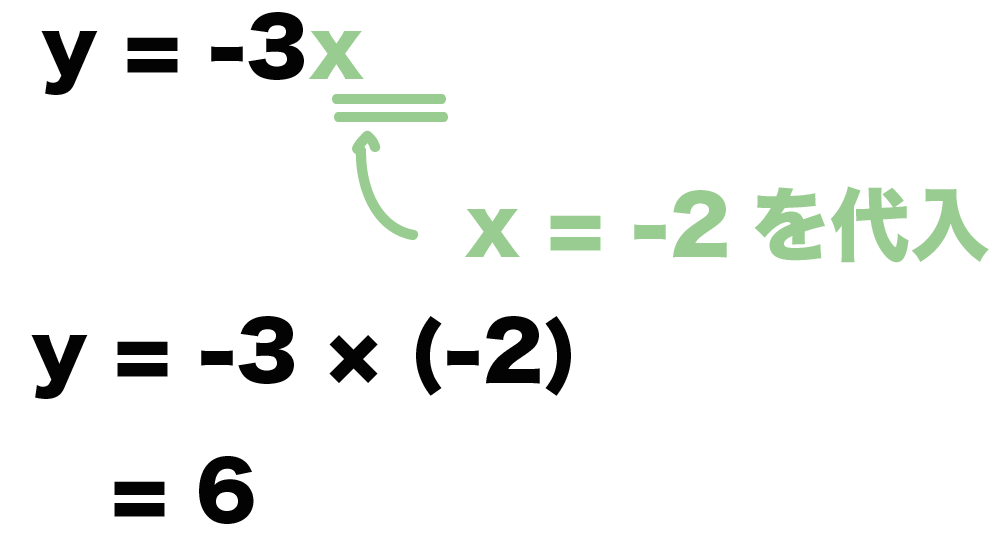
これで連立方程式の解がそろったね!
(x, y) = (-2, 6)
おめでとう!。
連立方程式の代入法は、
って感じで代入が2回もあってダルい。
だから、できれば代入法は使わないほうがいいね。
いつ、代入法をつかうべきなのか???
を見極めながら解き方を修得していってほしいね。
そんじゃねー
Ken