【中2数学】「逆」とはいったいなにもの？？
妖練習 連立方程式 スーパードリル 500
数学の「逆」とはいったいなにもの？？
こんにちは！この記事をかいているKenだよ。
中2数学を勉強していると、
逆（ぎゃく）
っていう言葉がでてくるね。
日常生活で「逆」ってことばはよく使う。
マリオカートをプレイすると、
おまえ、「逆」走してね？？
とかよく言うでしょ？
その「逆」だよ。
今日はその、
「逆」が数学ではどういう意味があるのか？？
をわかりやすく解説していくよ。
よかったら参考にしてみてね。
数学の「逆」の意味ってなんだろう？？
数学の「逆」とはずばり、
「あることがら」の「仮定」と「結論」を入れ替えたもの
さ。
たとえば、つぎのことがらがあったとしよう。
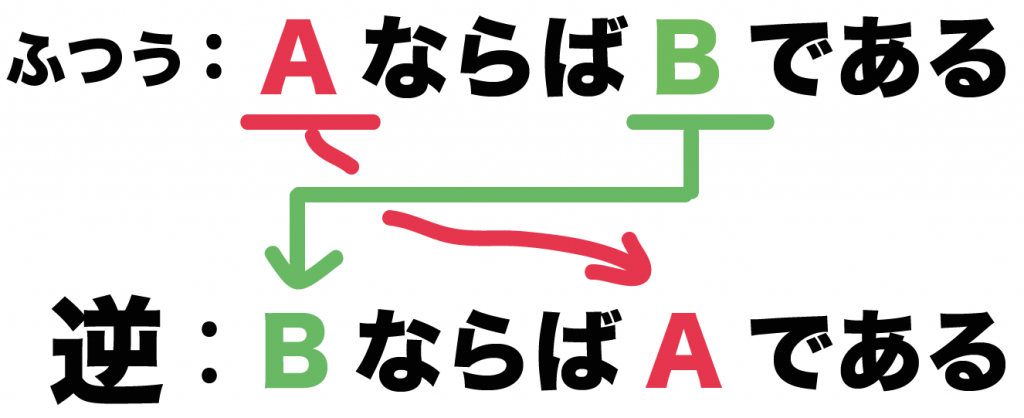
AならばBである
ってやつね。
こいつの逆をつくってみよう。
仮定がA、結論がBだね。
こいつらを入れ替えてやると、
BならばAである
ってなる。
たとえば、
馬ならば動物である
っていう「ことがら」があっとしよう。
このとき、
- 仮定＝「馬」
- 結論＝「動物」
だね。
だから、逆をつくるために、
仮定と結論をいれかえてやると、
動物ならば馬である
ってなるね。
数学の「逆」で注意するべき1つのこと
逆をつくるのは簡単だね。
だって、
「仮定」と「結論」を入れ替えるだけだから。
ただ、数学で逆をつくるときに知っておいてほしいのは、
あることが正しくても、その逆は正しいとは限らない
ということさ。
つまり、正しいことがらの逆をつくってみたけど、
逆をつくってみたら正しくなくなっちゃった・・・
ってことがあるってこと。
たとえば、さっきの馬の例をみてみよう。
馬ならば動物である
っていうことがらはどうだろう？？
こいつはただしそうだね。
だって、馬は動物だから。
だけれども、その逆をみてほしい。
動物ならば馬である
って正しくないよね？？
だって、動物は馬だけじゃないから。
ライオンだって、
ねずみだって、
牛だっている。
したがって、
馬ならば動物である
の逆は正しくないんだ。
数学ででてくる「逆」の2つの例
最後に、数学の逆の例を2つみてみよう。
- 逆にしても正しいことがら
- 逆にしたら正しくないことがら
逆にしても正しいことがら
平行線の性質は逆にしても正しいよ。
平行線の性質って、
2つの直線が平行ならば、同位角は等しい
だったね。
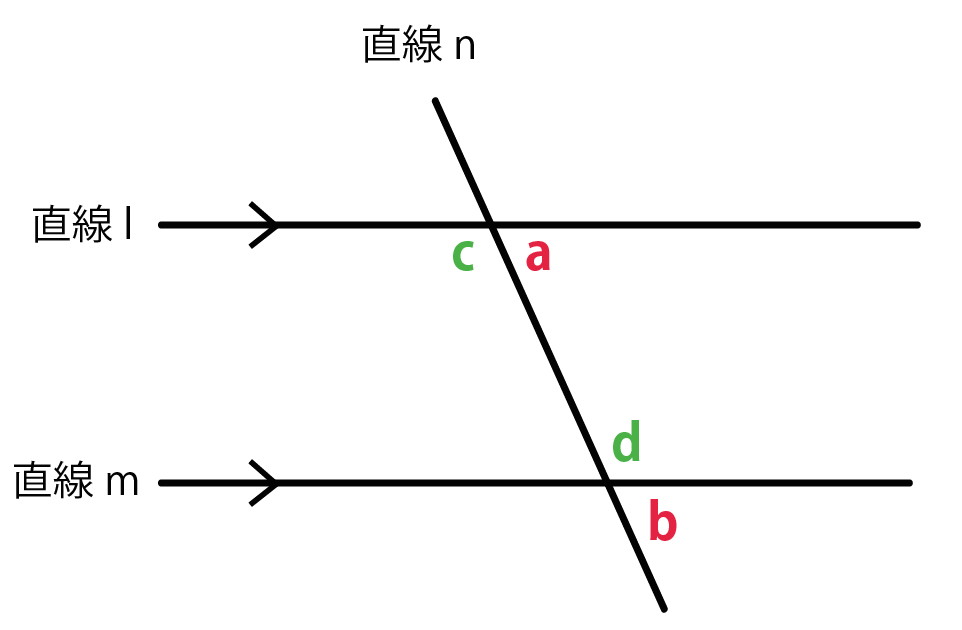
たとえば、
lとmが平行だったら、同位角のaとbが等しいってやつさ↓↓
じつは、この「平行線の性質」ということがらは、
逆も正しいといえるんだ。
つまり、
同位角が等しいならば、2つの直線が平行である
っていえるんだ。
たとえば、さっきの例でいうと、
同位角のaとbが等しかったら、直線lとmが平行になっている
ってことがいえるんだ。
逆にしたら正しくないことがら
合同な図形の性質は逆にしたら正しくなくなっちゃう。
合同な2つの図形には、
対応する角の大きさが等しい
っていう性質があったよね？
2つの図形が合同ならば対応する角が等しい
ってことが成り立っていたわけだ。
たとえば、△ABC ≡ △DEFだったら、
- 角A = 角D
- 角B = 角E
- 角C = 角F
ってことがいえるわけだね。
でも、ところがどっこい。
逆にしたら正しくなくなっちゃうんだ。
逆にすると、
対応する角が等しいならば2つの図形が合同である
になるでしょ？？
これはまちがっているね。
なぜなら、
ぜんぶの対応する角が等しくても合同じゃない場合があるからだ。
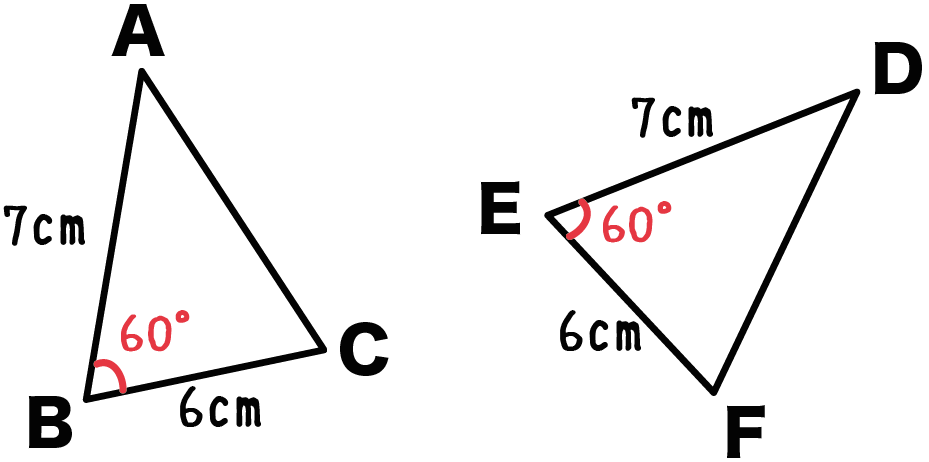
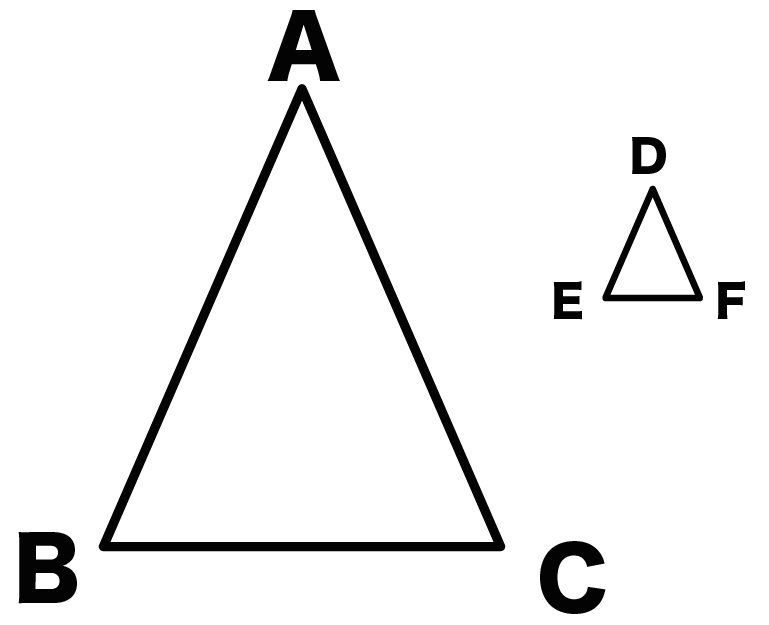
たとえば、下のような△ABCと△DEFみたいな感じでね。
こいつらは、
- 角A = 角D
- 角B = 角E
- 角C = 角F
なんだけど、
合同じゃないよね。
大きさ違いすぎて重ならないね。ゆえに、合同なんかじゃない。
これが逆が正しくない例だよ。
まとめ：逆は必ずしも正しくない！
逆の作り方は簡単。
だけれども、
逆が正しくないことがけっこうある。
っていうか、そのほうが多いね。
逆が正しいか？
正しくないか？
に注意して問題をといてみてね。
そんじゃねー
Ken
妖練習 連立方程式 スーパードリル 500
