二等辺三角形の定理を証明したいんだけど！
こんにちは！この記事をかいているKenだよ。スープは濃いめに限るね。
二等辺三角形の定理にはつぎの2つがあるよ。
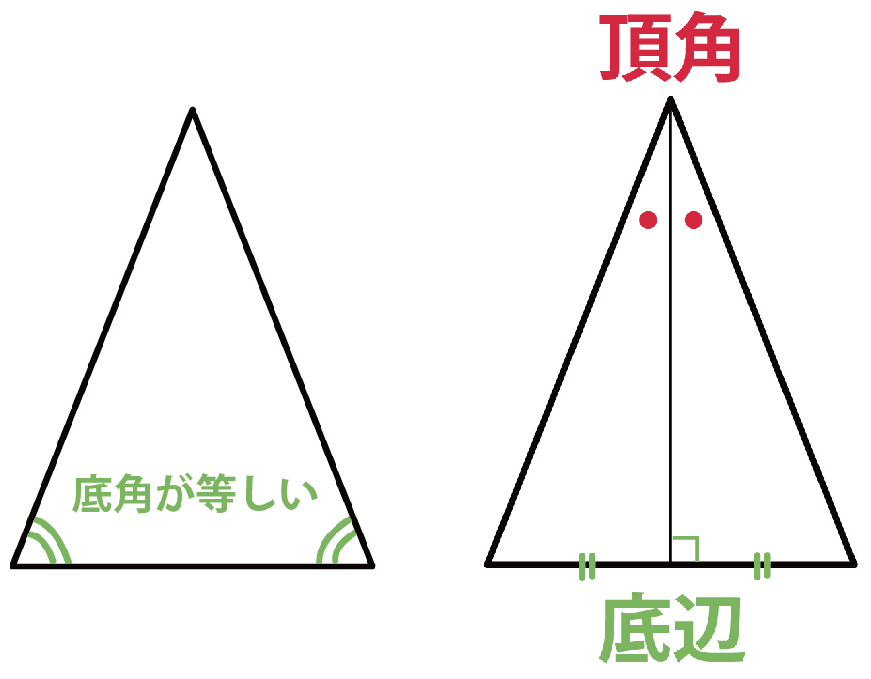
- 底角は等しい
- 頂角の二等分線は底辺を垂直に2等分する
こいつらって、むちゃくちゃ便利。
証明で自由に使っていいんだ。
でもでも、でも。
疑い深いやつはこう思うはず。
なぜ、二等辺三角形の定理を使っていんだろう？？
ってね。
そんな疑問を解消するために、
二等辺三角形の定理を証明していこう！
二等辺三角形の定理の証明がわかる3ステップ
つぎの、
二等辺三角形ABCで証明していくよ。
AB = ACのやつね。
3つのステップで証明できちゃうんだ。
Step1. 頂角から底辺に二等分線をひく！
頂角から底辺に二等分線をひこう。
例題でいうと、
Aの二等分線を底辺BCにひいてやればいいんだ。
底辺との交点をHとするよ。
Step2. 三角形の合同を証明する！
三角形の合同を証明していくよ。
例題でいうと、
- △ABH
- △ACH
の2つだね。
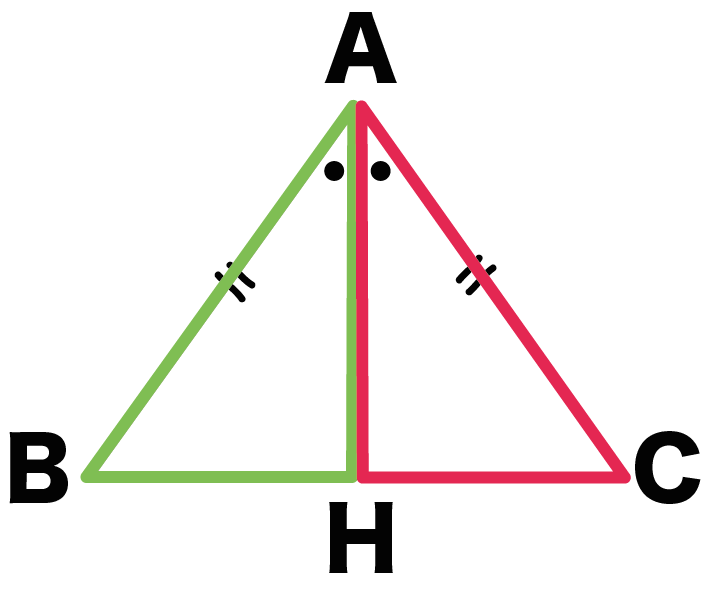
△ABHと△ACHにおいて、
仮定より、
AB = AC・・・(1)
AHは角Aの二等分線だから、
角BAH = 角CAH・・・(2)
辺AHは共通だから、
AH = AH・・・(3)
(1)・(2)・(3)より、
2組の辺とその間の角がそれぞれ等しいので、
△ABH ≡ △ACH
である。
これで2つの三角形の合同がいえたね！
Step3. 合同な図形の性質をつかう！
あとは、
- 対応する線分の長さは等しい
- 対応する角の大きさは等しい
をつかうだけ！
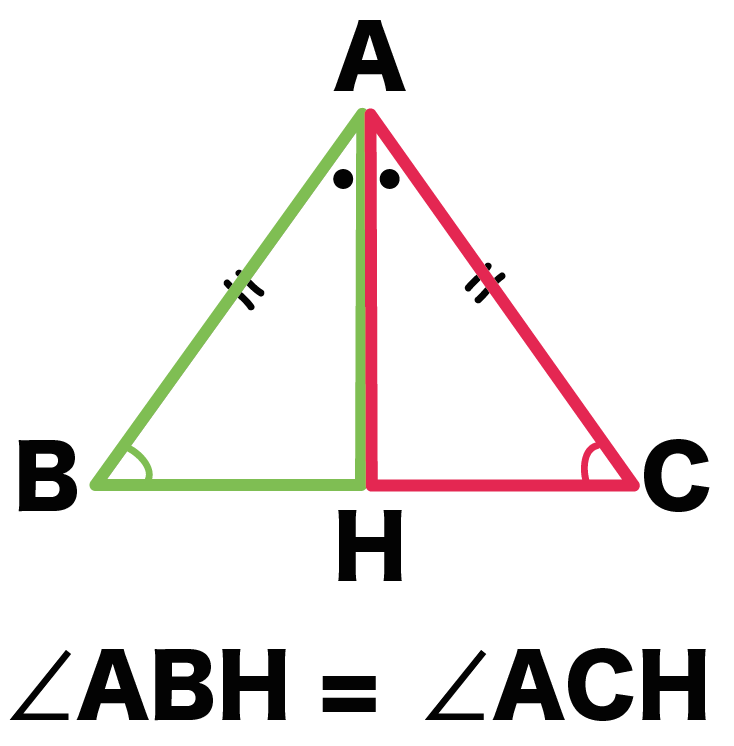
合同な図形同士の対応する角は等しいので、
角ABH = 角ACH
だ。
こいつらは底角だから、
二等辺三角形の底角が等しい
ってことを証明できたね。
また、対応する角が等しいから、
角AHB = 角CHB
でもあるはずだ。
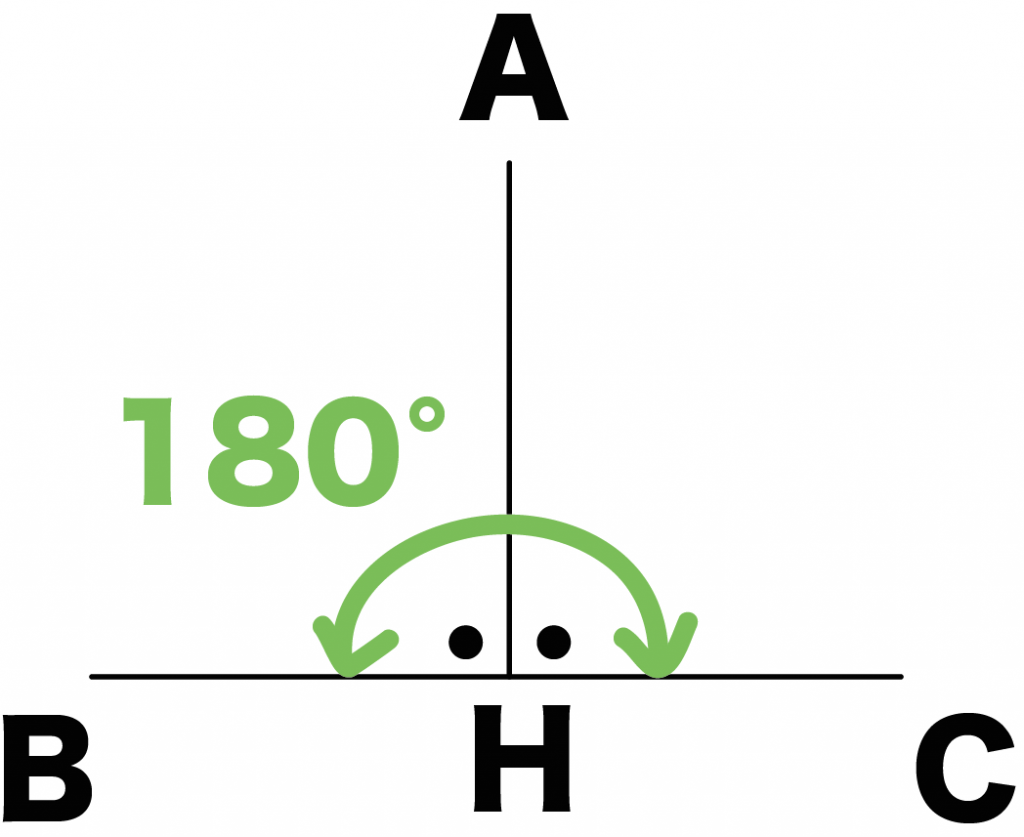
角AHB と角CHBはあわせて一直線になっている。
つまり、
角AHB + 角CHB = 180°
だね？
ってことは、
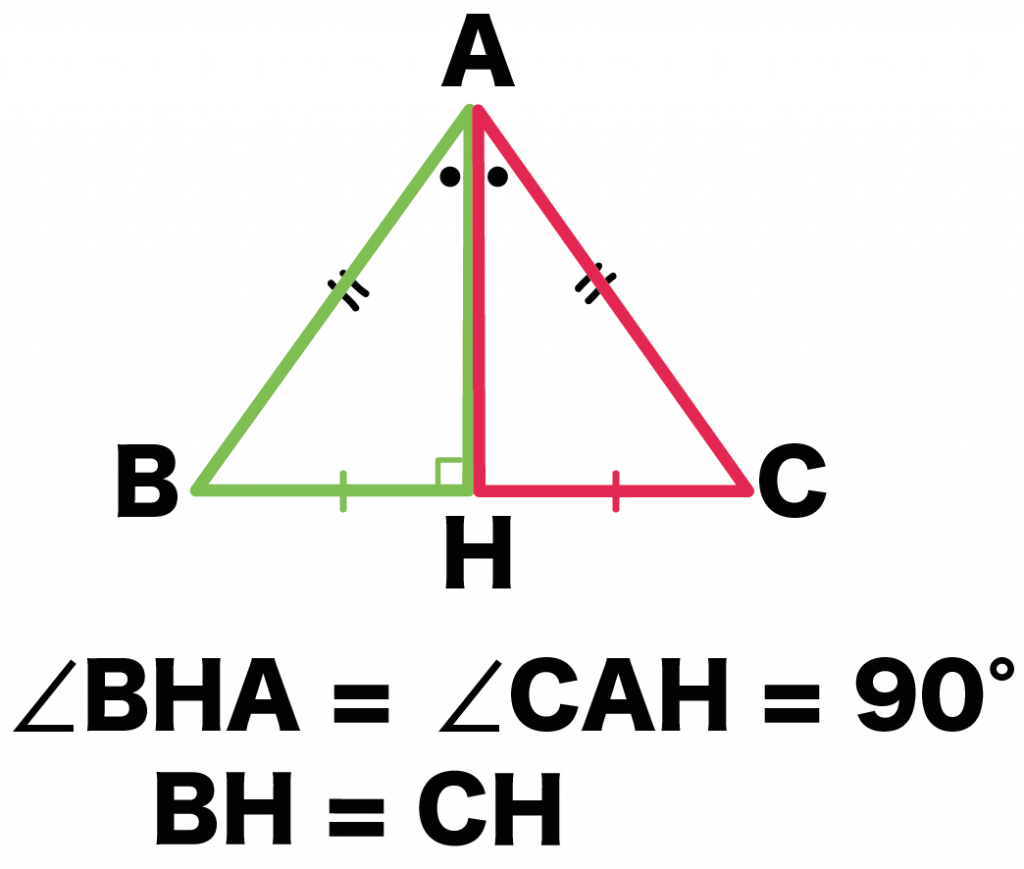
角AHB = 角CHB = 90°・・・(4)
であるはずさ。
対応する辺も等しいので、
BH = CH・・・(5)
だよ。
ってことは、
二等分線AHは底辺BCの垂直二等分線
になっている！
つまり、
頂角の二等分線は底辺を垂直に二等分する
ってことがわかったね。
まとめ：二等辺三角形の定理の証明は合同の性質から！
二等辺三角形の定理は便利。
ぜんぶ、
合同な三角形の性質からきているんだ。
暗記するのも大事だけど、
なぜ、二等辺三角形の定理がつかえるのか？？
ということを知っておいてね。
そんじゃねー
Ken
