【1次関数の公式】変化の割合の求め方がわかる3つのステップ
一次関数の変化の割合の求め方がわからんねえ!
こんにちは!この記事をかいているKenだよ。本屋にいきたいね。
一次関数の問題で、
変化の割合をもとめろ!!
ってヤツがよくだされる。
こいつは、変化の割合の公式、
(変化の割合)=(yの増加量)÷(xの増加量)
をつかえば攻略できるよ。
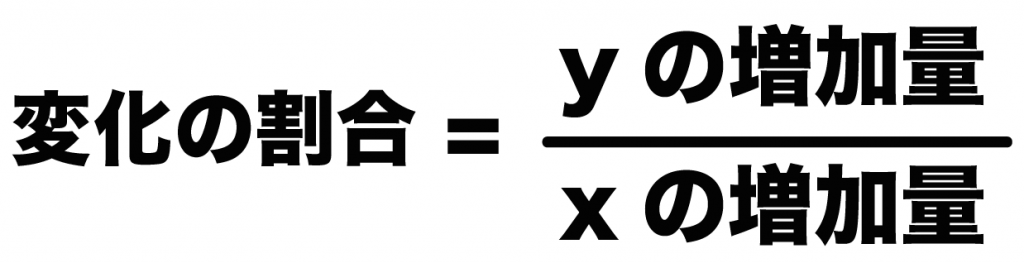
たとえば、
xの増加量が5のとき、yの増加量が25の関数があったとしよう。
こいつの変化の割合は、
(yの増加量)÷(xの増加量)
= 25 ÷ 5
= 5
になるんだ。
公式ならすぐ計算できちゃうでしょ??
今日はこの公式を使って、
1次関数の変化の割合の求め方
を3つのステップで解説していくよ。
テスト前に参考にしてみてね。
一次関数の「変化の割合」の求め方がわかる3ステップ
例題で「変化の割合」をもとめてみよう!
例題
xが3から6に変化したとき、yの値が8から-1になる一次関数があったとしよう。
この一次関数の変化の割合をもとめよ!
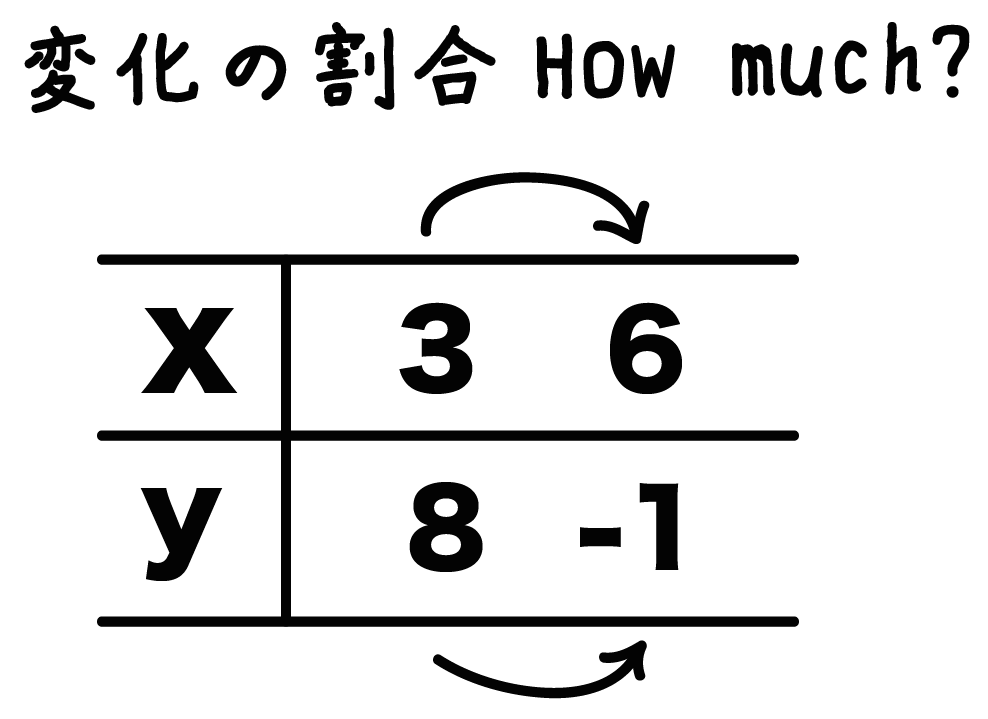
つぎの3ステップで攻略できちゃうよ!
Step1. 「xの増加量」をもとめる!
まず「xの増加量」から計算しよう。
xの増加量の求め方は、
(変化の後のxの値)- (変化の前のxの値)
だ。
つまり、ゴール地点からスタート地点のxの値をひいてやればいいんだ。
例題では、
xの値は「3」から「6」 に変化したんだよね??
ってことは、このときのxの増加量は、
(変化の後のxの値) – (変化の前のxの値)
= 6 – 3
= 3
になるよ!
Step2. 「yの増加量」を計算する!
yの増加量をもとめてみよう!
「yの増加量」も「xの増加量」とおなじで、
(変化の後のyの値)- (変化の前のyの値)
で計算できるよ。
例題をみてみよう。
yの値は「8」から「-1」まで変化してるよね??
yの増加量を
(変化の後のyの値)- (変化の前のyの値)
で計算してやると、
-1 – 8
= -9
になるね。
yの増加量は「-9」ってことだよ。
勘の鋭いヤツはここで、
えっ。yの増加量がマイナスっておかしくね??
って思うはずだ。
ぶっちゃけ、暴動がおきてもおかしくない。
ここで覚えておいてほしいのは、
増加量がマイナス(負の数)になる場合もありえる
ということだ。
xとかyの増加量ってただの表記であって、
かならずしもプラスになっているとは限らない。
増加量というより、
xとyの「変化量」と捉えたほうがわかりやすいかもね。
Step3. 「yの増加量」を「xの増加量」でわる!
xとyの増加量をゲットしたね?
あとは公式で計算してやるだけさ。
(変化の割合)=(yの増加量)÷(xの増加量)
を使ってみてね。
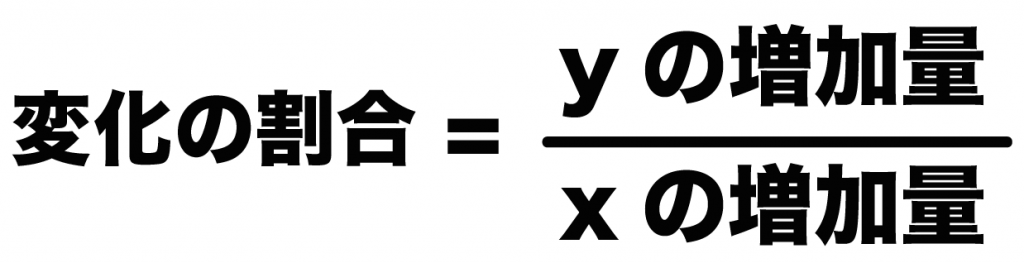
例題をみてみて。
xとyの増加量って、
- xの増加量:3
- yの増加量:-9
だったよね??
こいつらを公式で計算してやると、
(変化の割合)
=(yの増加量)÷(xの増加量)
= – 9 ÷ 3
= – 3
になるよ。
変化の割合は「-3」になったね。
つまり、
この1次関数はxが1増えるごとに、yが3減る野郎だってことさ。
変化の割合の意味がイマイチ・・・・
ってときは、
一次関数の変化の割合の記事で復習してみてね。
まとめ:一次関数の変化の割合の求め方は公式で1発!
変化の割合の求め方はわかった!?
(変化の割合)=(yの増加量)÷(xの増加量)
っていう公式で計算していこう。
問題をといて計算になれてみてね。
そんじゃねー
Ken



