3分でわかる!連立不等式の解き方

ここまでで基本的な不等式の解き方をマスターしたよな。
でもな、これで許してくれないのが数学ってもんよ。
次は、
連立不等式(れんりつふとうしき)
が登場するぜ。
連立不等式とは、
2つ以上の不等式が1つのグループになったものだ。
例えば次のような感じ。
$$\begin{cases} 2x+1<x-3 & \\ -5x+7≧-8 & \end{cases}$$
複数の不等式が共通で満たす解の範囲を求めることを、
連立不等式の解
と人間界では呼んでいて、その解を求めることを
連立方程式を解く
って言うぞ。
この連立不等式の解き方は次の3ステップだ。
連立不等式の解き方3ステップ
それじゃ3ステップ踏んでいくぞ。さっきの例題を一緒に解いてみよう。
$$\begin{cases} 2x+1>x-3 & \\ -5x+7≧-8 & \end{cases}$$
不等式をそれぞれとく
まずは組になっているそれぞれの不等式を1つずつ解いていくんだ。
このステップでは、2つの不等式の関係は一切無視!
一つ一つにしっかり向き合ってくぜ。
$$\begin{cases} 2x+1>x-3 & \\ -5x+7≧-8 & \end{cases}$$
をバラしてやって、
$$2x+1>x-3$$
と
$$-5x+7≧-8$$
をそれぞれとこう。
すると、次のように2つの不等式の解が出てくるよな。
$$x>-4$$
$$x≦3$$
数直線を書く
ここで出てくるのが数直線だ。
数直線とは、
数の大小関係を直線上に表したもの
だったな。
これは中学数学でも出てきた内容だから思い出してくれ。
数直線は書かなくてもゲームオーバーにならないが、書いたほうがわかりやすいからオススメだ。
数直線を書いた方が、
複数の不等式の解の共通範囲がわかりやすいんだな。
数直線で不等式の解の範囲を表すときに1つ注意してくれ。
それは、
不等式の解の境界だ。つまり、領域の端っこのことな。
境界を含む時は「●」で塗りつぶし、境界を含まないんだったら「○」にしてやろう。
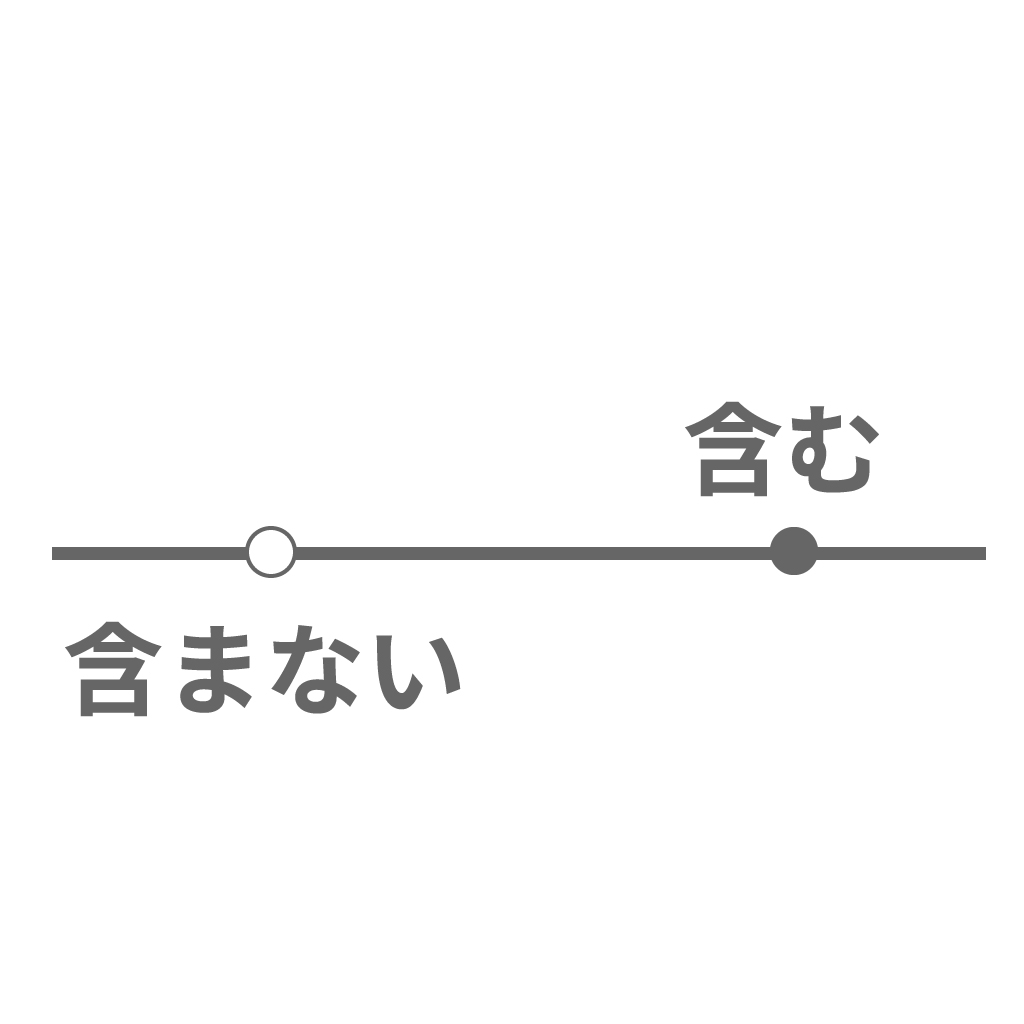
不等式は「境界を含むか含まないか」が大事だ。ここをミスっちまうとどんなに善良な人間だろうが不正解になっちまうおそろしい世界だ。
で、
例題の不等式の解を数直線を書いてみると次のようになる。
$$x>-4$$
$$x≦3$$
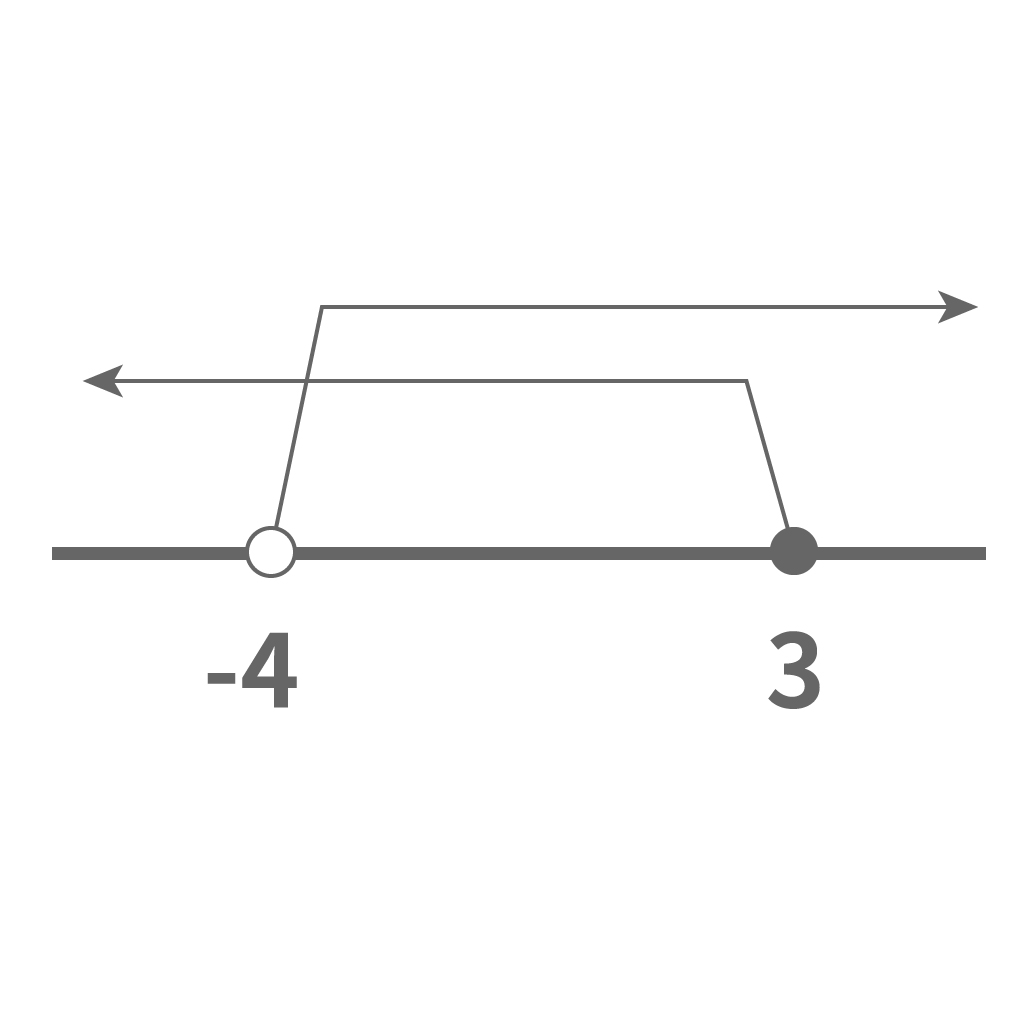
解の共通範囲を求める
最後に、数直線から2つの不等式の解の共通範囲を求めよう。
2つの不等式の解の範囲がかぶっている範囲
を探せばいいんだな。
数直線で書いてみて、被っている領域を発見したら、斜線を引いたり、塗りつぶしてやったりして、視覚的にわかりやすくするといいな。
さっきの例では、ここが共通範囲。
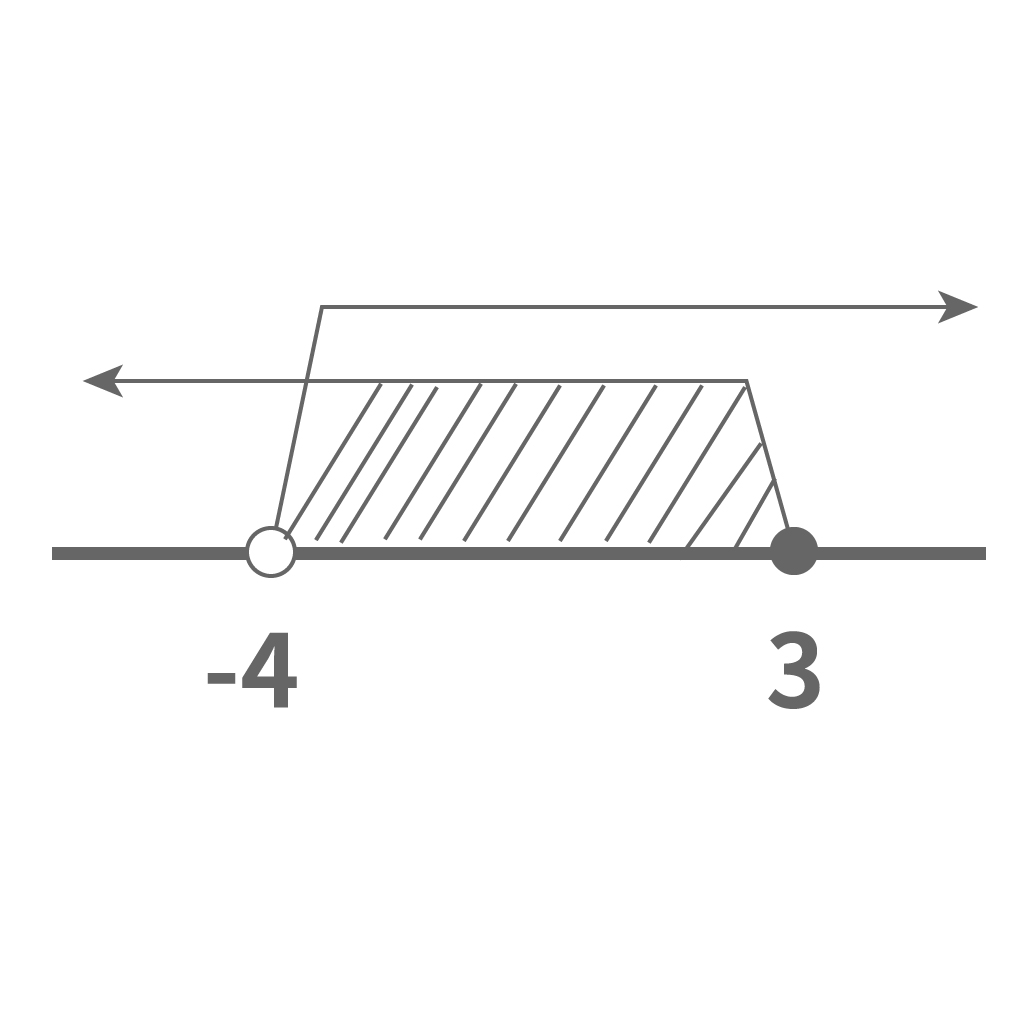
したがって、この斜線の範囲が連立不等式の解になる。
この被り領域を不等号で表すと次のようになるな。
$$-4<x≦3$$
これが連立不等式の解だ!
不等式が { でつながっていない連立不等式
でもな、たまに { でつながっていない連立不等式もあるんだ。
例えば次のようなやつだな。
$$2x+1<x-3<-5x+7$$
1直線上に不等号が連なっていてるパターン。
一見奇妙に見えるが、これも連立方程式の一種だ。
この場合、
最初に2組の不等式に分けてやるんだ。
一直線になってる連立方程式は、次のように2つの不等式に分けられるからな。
$A < B < C$
だったら
- $A< B$
- $B < C$
に分けられるんだ。
つまり、
$$2x+1<x-3<-5x+7$$
は
$$\begin{cases} 2x+1<x-3 & \\ x-3<-5x+7 & \end{cases}$$
になる、と。
2組の不等式にわけたら、それぞれ解いてやって、解の共通範囲を求めてやれば万事OKさ。

それじゃあな!


