【カンタン公式】扇形の中心角の求め方がわかる3つのステップ
扇形の中心角の求め方の公式を知りたい!

「扇形の中心角の求め方」の公式ってチョー便利。
教科書にはのっていない「知る人ぞ知る公式」なんだ。
扇形の中心角をx°、弧の長さをL、半径をrとすると、
x = 180L/πr
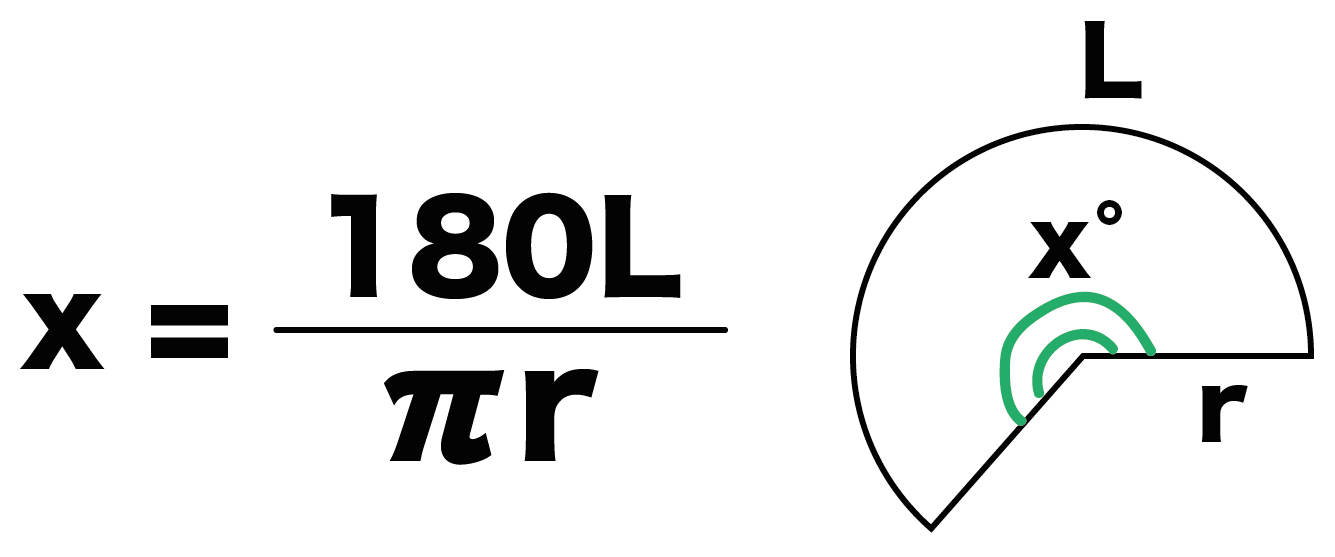
になるってやつさ。
つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。
たとえば、
半径 4 [cm]、弧の長さが 6π [cm]の扇形があったとしよう。
この「扇形の中心角」を求めたいときは公式をつかえば一発。
3秒ぐらいで中心角が求められるよ。
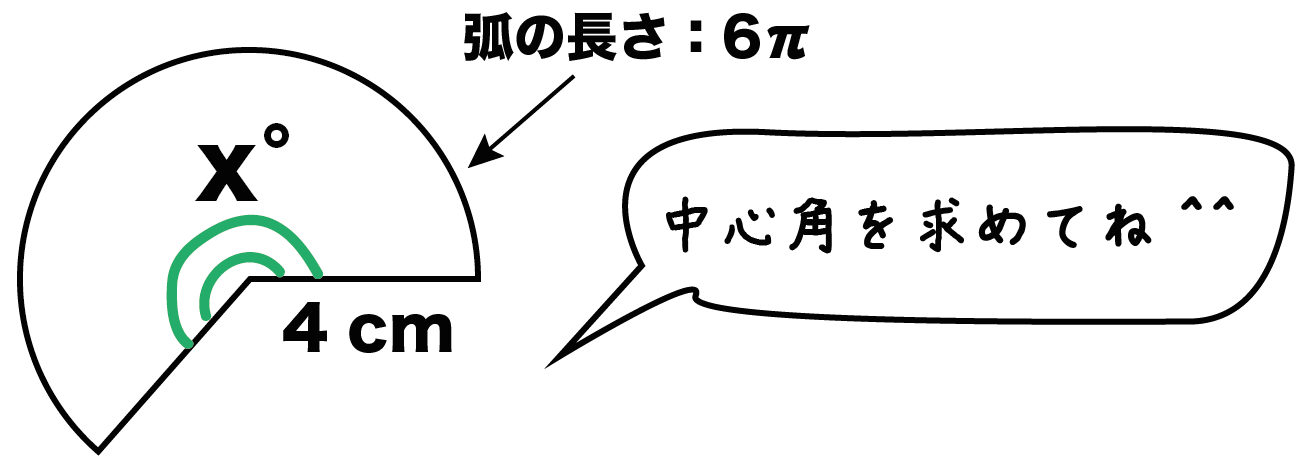
中心角の公式は、
x = 180L/πr
だったよね? これに半径r=4cm、弧の長さL= 6πを代入してやると、
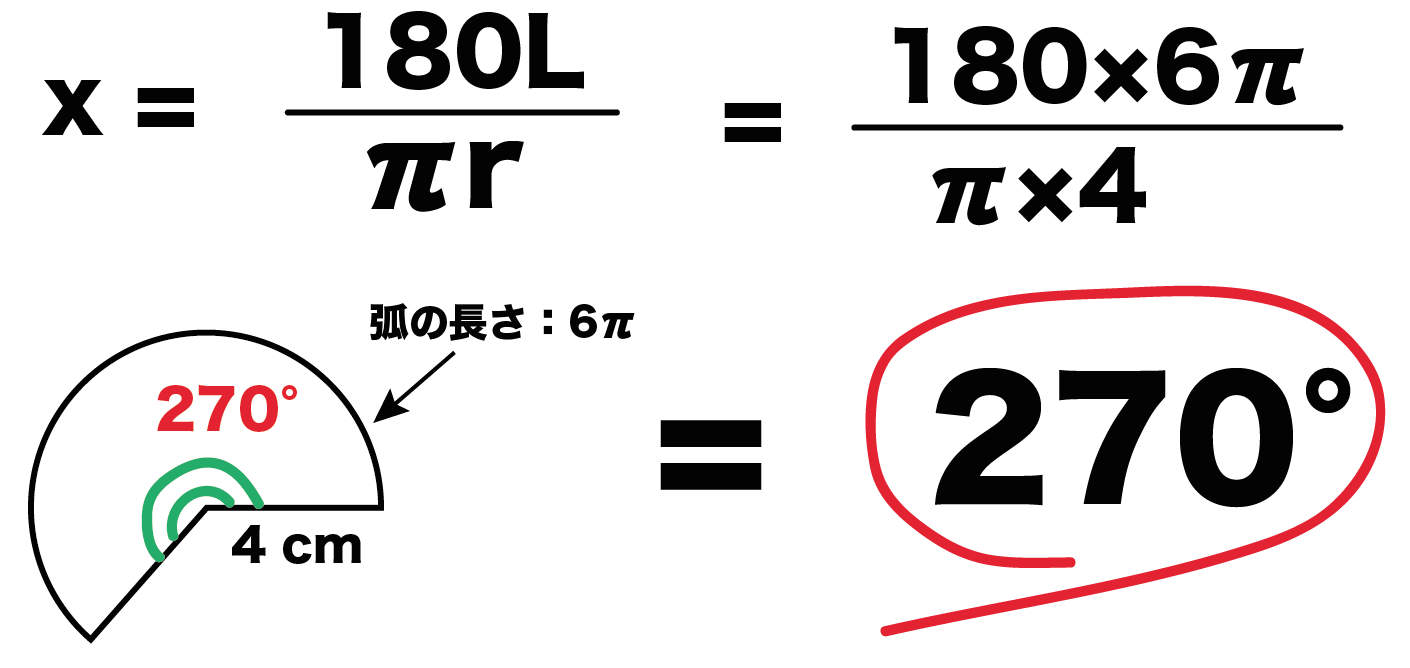
x = 270°
っていう答えがえられる。
これが中心角だよ。ものすごく簡単で便利でしょ??
公式をつかわない!扇形の中心角の求め方3つのステップ
それじゃあ、なぜこの公式で扇形の中心角が求められるのか??
ちょっと気になるよね??
じつは、扇形の中心角の公式は、
比例式をつかった中心角の求め方
から導きだしたものなんだ。
ってことは、「比例式から求める方法」を知っておけば公式を忘れても大丈夫ってことになる。
念のために、公式に頼らない「扇形の中心角の求め方」をみていこう。
さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。

中心角はつぎの3ステップで計算できるんだ。
Step1. 扇形の中心角をx°とおく
まずは「扇形の中心角」を「x°」とおいてみよう。
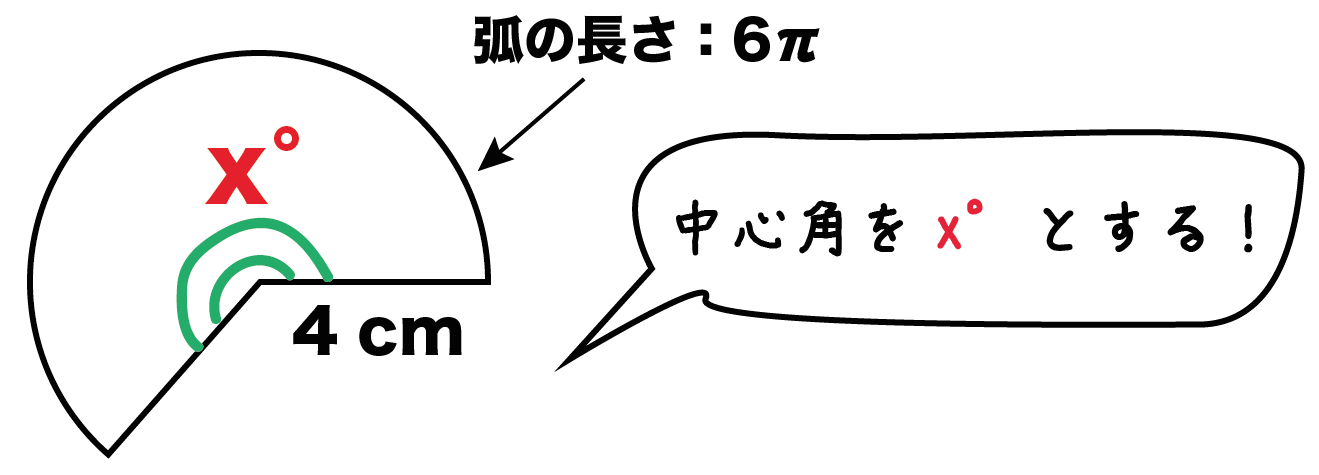
これは方程式の文章題と同じ。
「求める値」をxとするのが定石なんだ。
Step2. 比例式をたてる
つぎはいよいよ比例式をたてるステップ。
「扇形の弧の長さ」は「中心角の大きさ」に比例する、
っていう性質をつかってあげよう。
すると、
円の「中心角」と「円周の長さ」、扇形の「中心角」と「弧の長さ」で
比例式をたてることができるよ。
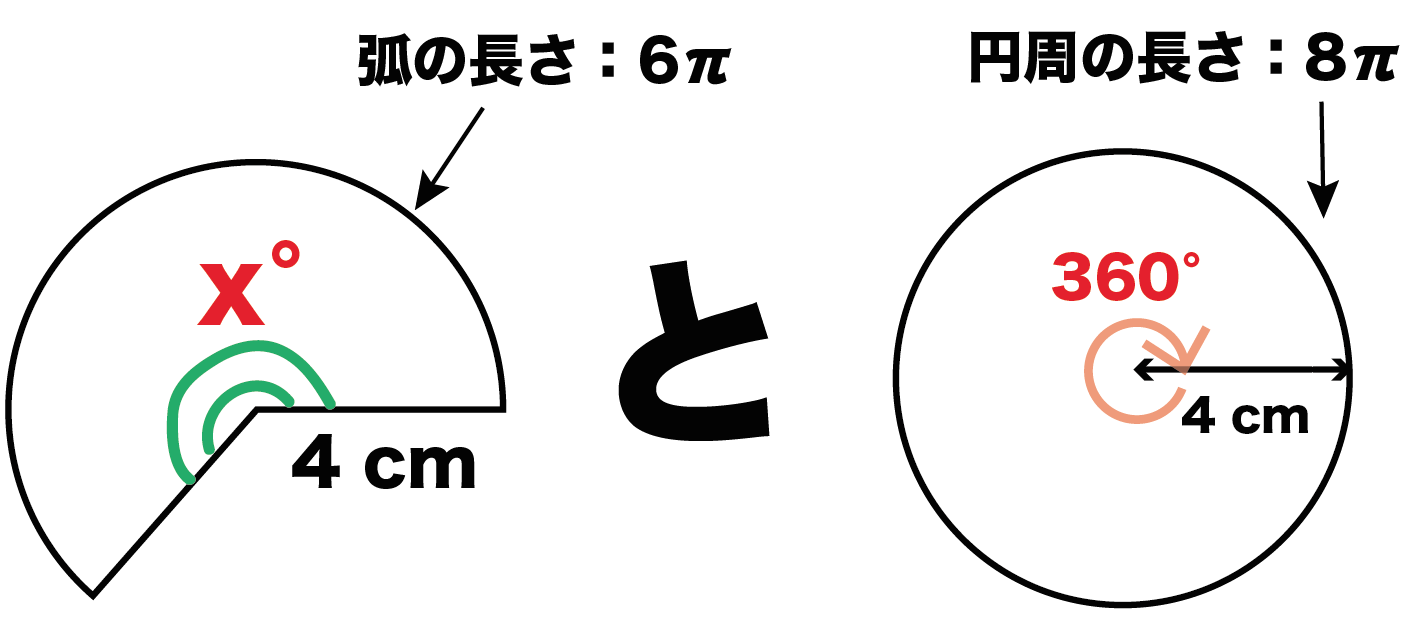
左辺を「中心角の比」、右辺を「弧の長さの比」で比例式をたててみよう。すると、
(扇形の中心角):(円の中心角) = (扇形の弧の長さ):(円周の長さ)
x : 360 = 6π : 8π
ってなるよー。
Step3. 比例式を「内項・外項の積」でとく!
あとはこの比例式をといてやるだけ!
もし、比例式の解き方を忘れちゃったときは「【比例式の性質】3分でわかる!比例式の解き方」っていう記事を復習してみてね。
比例式は「内項・外項の積」で一発でとける。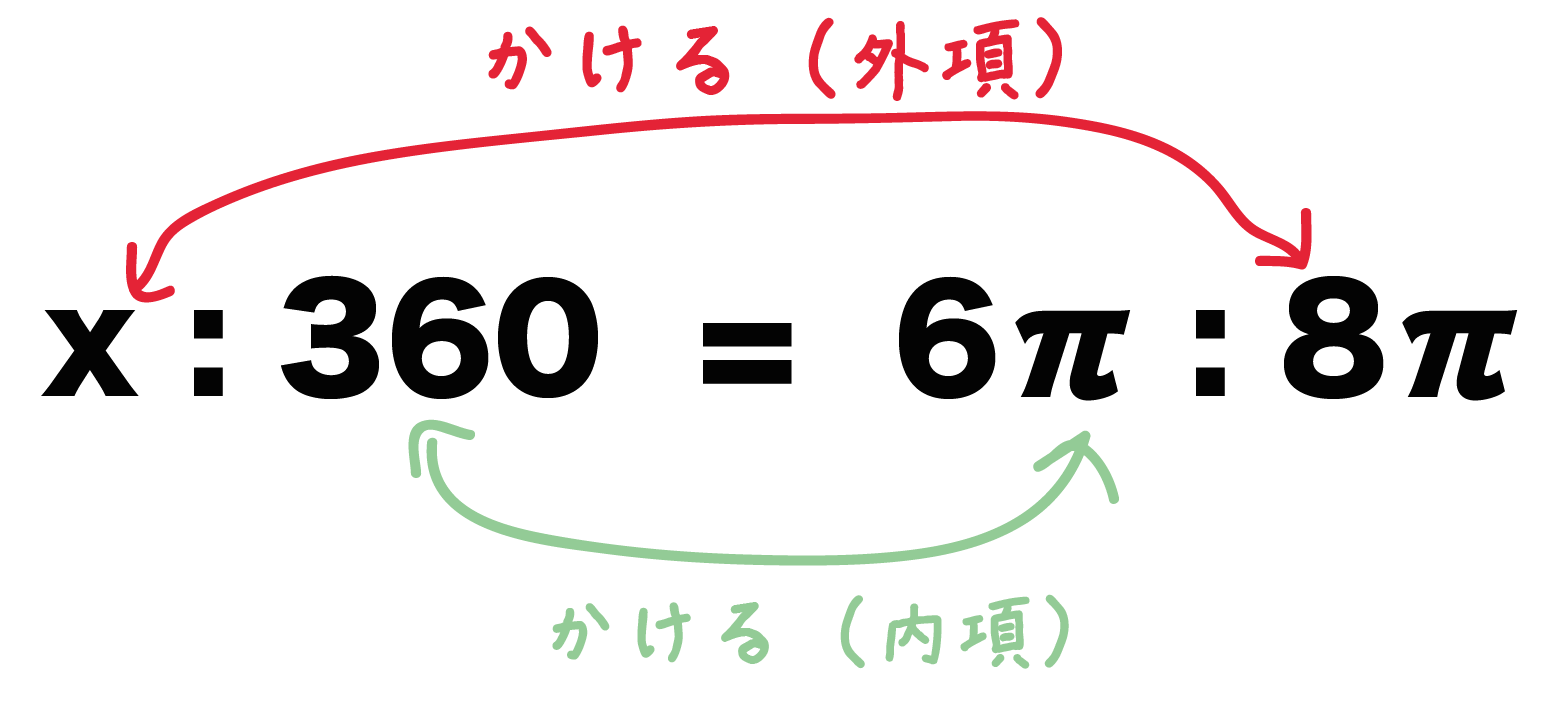
つまり、比の「外側同士をかけたもの(外項)」と「内側同士をかけたもの(内項)」を等式にしてやればいいんだ。
すると、
x × 8π = 6π × 360
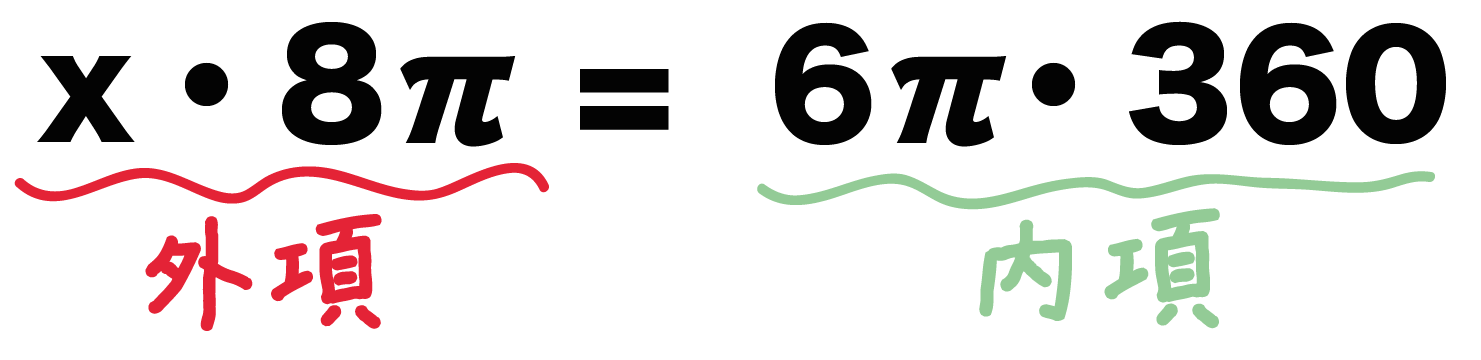
っていうxについての方程式ができるね。
こいつを解いてやると、
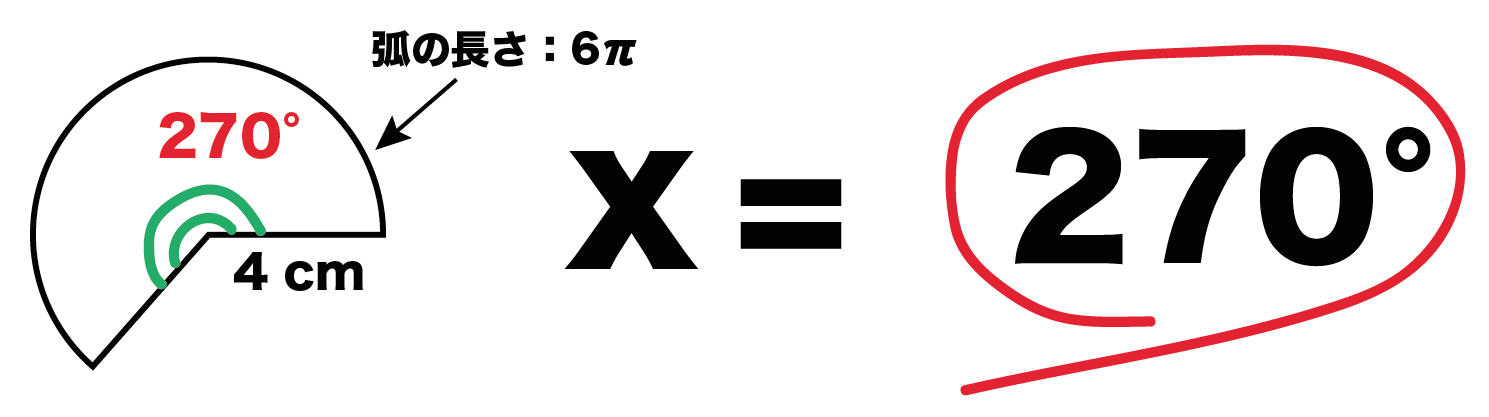
x = 270
っていう解がでてくる。このことから、
「半径4cm、弧の長さ6π cm」の扇形の中心角は270°になるってことがわかる!
まとめ:扇形の中心角の求め方は意外と簡単!
めんどくさいときは公式で扇形の中心角を求めてもいいよ。
だけど、

なぜなら、公式は教科書にのってないからさ。
数学の先生たちは「扇形の中心角の求め方」の思考プロセスがみたいんだ。だから、計算式をかけよ!っていう問題にしてくるかもしれないぜ。
そんじゃねー




