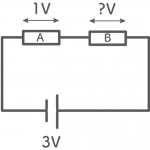
テストで狙われやすい!並列回路の電圧・電流・抵抗の求め方
並列回路の電圧・電流・抵抗の求め方がわからん!
こんにちは!この記事を書いているKenだよ。お湯、汲んできたね。
中学理科の電気で狙われやすいのが、並列回路の電圧・電流・抵抗の求め方。
前回勉強してきた「直列回路の電圧・電流・抵抗の求め方」とは異なるから、並列回路は並列回路のルールを覚えなきゃいけないんだ。
今日はそのテストにも出やすい並列回路の電圧・電流・抵抗の求め方をわかりやすく解説してみたよ。
並列回路の電圧の求め方
まず電圧からだね。
並列回路の電圧のルールはすこぶる簡単。
それは、
全体の電圧は各抵抗にかかる電圧に等しい
ってやつだ。
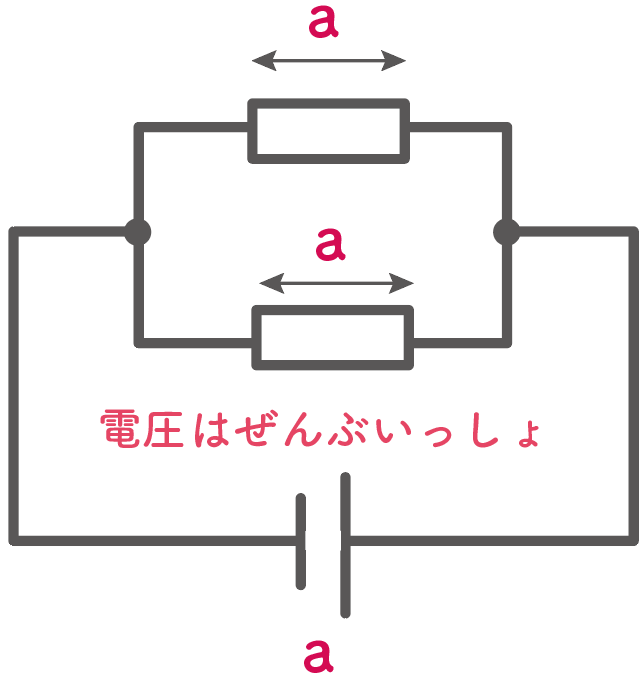
どの抵抗だろうが電球だろうが、並列に繋がっているなら、そこにかかる電圧は同じってことね。
例えば、 3Vの電源に2つの抵抗A・Bを並列につなげているところを想像してみて。
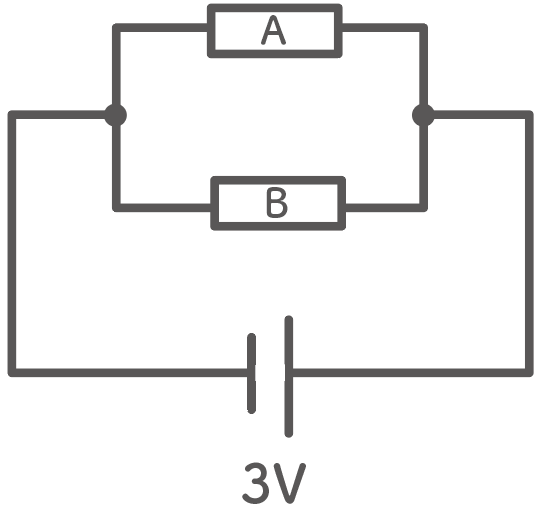
このとき抵抗 A・ B 、それぞれにかかる電圧はなんと。
3V!!
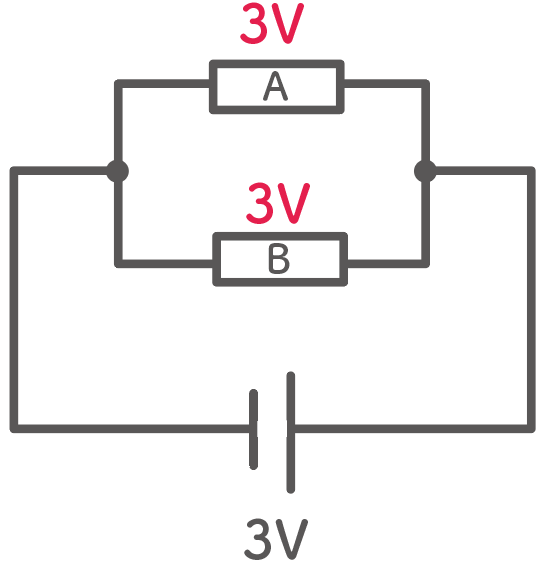
電源の電圧と全く同じってことなんだ。らくしょ〜
並列回路の電流の求め方
次は電流だね。
並列回路の電流は次のルールを覚えておけばいいよ。
枝分かれして電流を足すと全体に流れる電流になる
ってやつ。
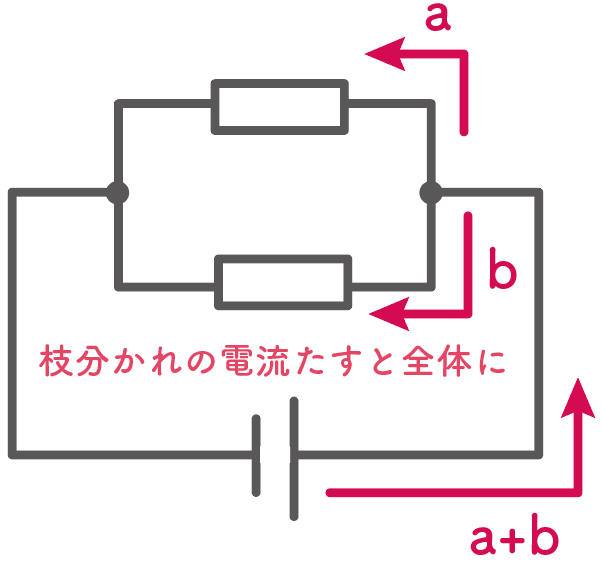
どういうことか具体的に説明していくね。
例えば、全体の枝分かれする前の電流の大きさが3[A]だとしよう。
この時、抵抗Aに流れる電流が2[A]だったとしたら抵抗Bに流れる電流はいくらになるだろうか???
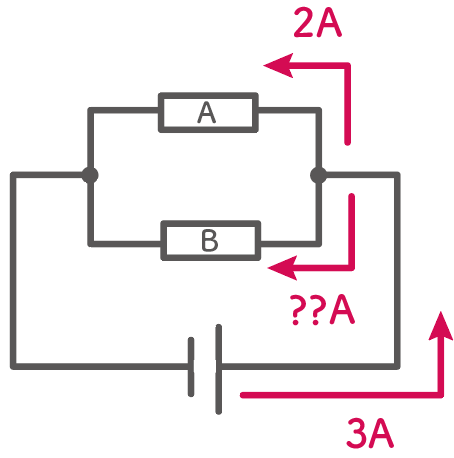
そう、そうだよ。
全体の電流3 [A]から抵抗に流れる電流の2 [A]を引いて1 [A] 流れるというのが正解だ。
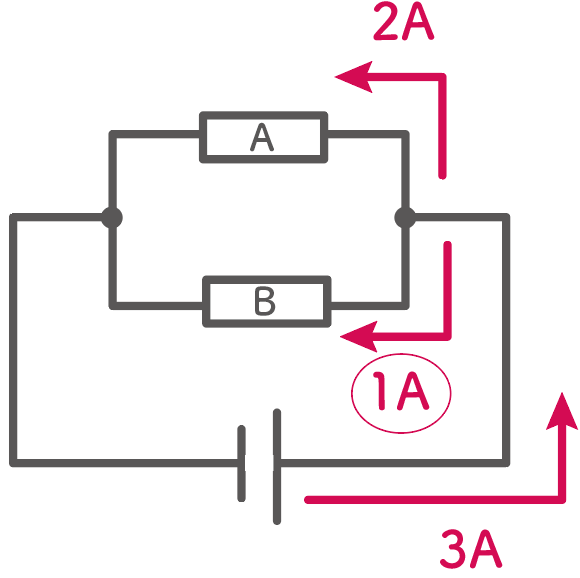
枝分かれの電流を足したら、全体の電流になると覚えておけばいいね。
並列回路の抵抗の求め方
最後に並列回路の抵抗の求め方だね。
これは若干トリッキーなので注意が必要。並列回路のルールは次のものになるよ↓
全体の抵抗の逆数は各抵抗にかかる抵抗の逆数を足したものに等しい
だ。
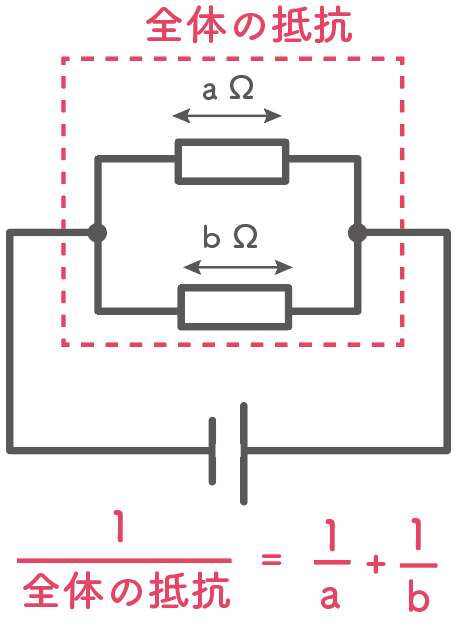
ちょっとわかりづらいから具体例で見てみよう。
例えば、2つの抵抗が並列回路で繋がっていて、抵抗Aが200Ω、抵抗Bが100Ωだとする。
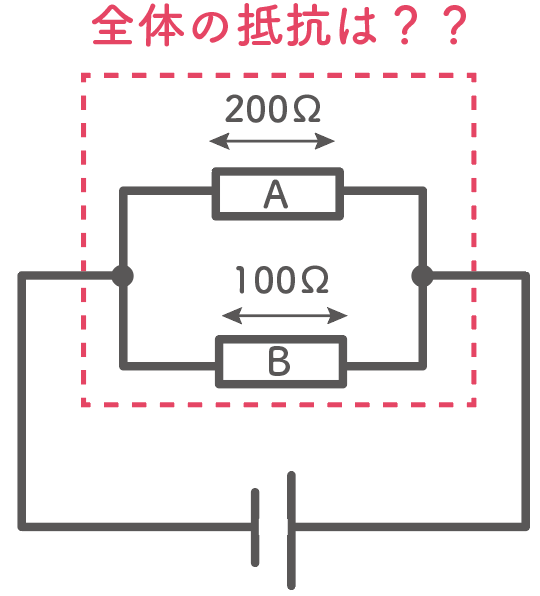
この時、2つの抵抗を合わせた全体の抵抗値を求めるとしよう。
さっきの並列回路の抵抗のルールを適用すると、2つの抵抗の逆数を足したものになるから、
(Aの抵抗値)分の1 +(Bの抵抗値)分の1 = (全体の抵抗値)分の1
となるわけだね。
これをさっきの電気回路に当てはめて全体の抵抗を求めてみるよ。
(Aの抵抗値)分の1 +(Bの抵抗値)分の1 = (全体の抵抗値)分の1
200分の1 + 100分の1 = (全体の抵抗値)分の1
200分の3 = (全体の抵抗値)分の1
(全体の抵抗値)= 3分の200 ≒ 66.6666Ω
になるね。
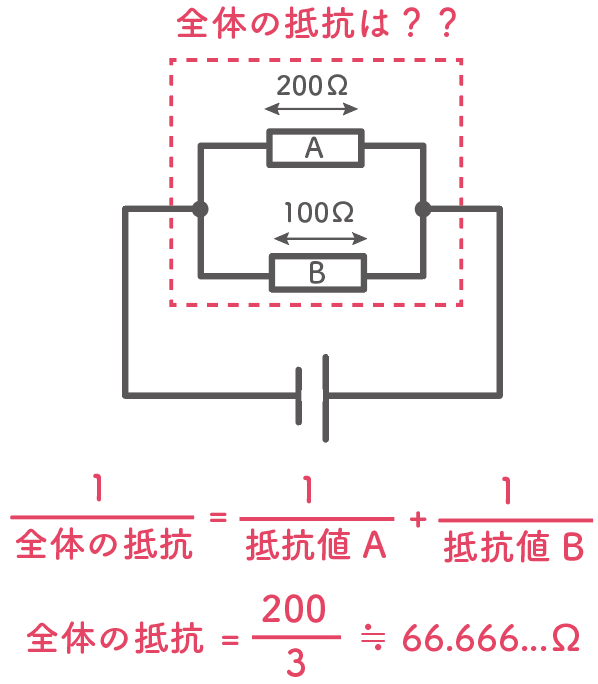
このことから分かるのは、
全体の抵抗はそれぞれの抵抗よりも小さくなるってことだ。
66.66という抵抗値はもちろんAの抵抗値200Ωよりも小さいし、もう一個のBの抵抗値の100Ω よりも小さいよね。
んな感じで、全体の抵抗を求めると小さくなってしまうのが、並列回路の抵抗なんだ。
基本ルールを抑えれば並列回路も攻略だ!
以上が並列回路の電圧・電流・抵抗の求め方だったよ。
最後におさらいしておこう。
並列回路の電圧は電源の電圧と同じでどこでも電圧は等しいね。

電流は枝分かれを足したものが全体の流れる電流になって、

全体の抵抗の逆数は、各抵抗にかかる抵抗の逆数を足したものに等しい
と覚えておこう。

次は「電圧計の使い方」を勉強していこう。
そんじゃねー
Ken