【線対称の作図】4つのステップでわかる!対称移動の書き方
対称移動(線対称)の書き方がよくわからない??
こんにちは、目玉焼きが得意なKenだよー!今日も一緒に中学数学の勉強をはじめよう!!
図形の移動方法のうち、
という2つの移動方法についてみてきたね。
今日は、残りの「対称移動(線対称)」の書き方を勉強していこう。

これをマスターしちまえば、図形の移動をすべて網羅したことになる。
数学のテストで高得点は間違いないさ。
~もくじ~
- 線対称の性質
- 対称移動の書き方4つのステップ
対称移動(線対称)の性質が重要??
対称移動の書き方を勉強する前におさえておきたいことが1つある。
それは、
対称移動(線対称)の図形の性質だ。教科書によると、線対称の図形には、
対応する点を結んだ線分は、対応の軸と垂直に交わり、その交点で二等分される
って書いてあるね。
たとえば、三角形ABCを「対称の軸(直線m)」で対称移動させたとしよう。
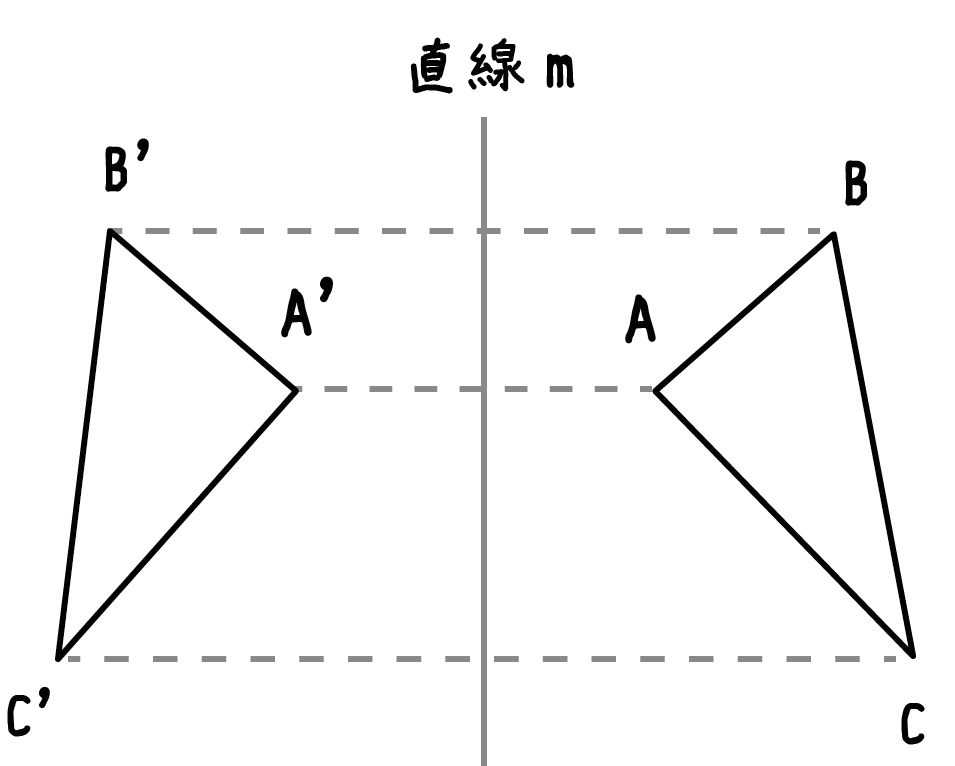
このとき、直線mと「対応する点を結んだ線分」たちは垂直に交わっていて、
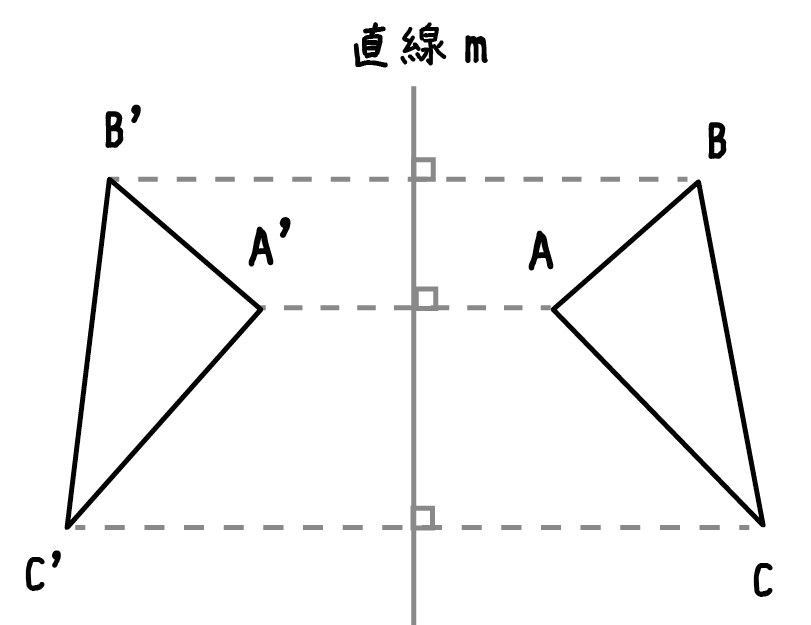
交点が2点の中点になっているということなんだ。
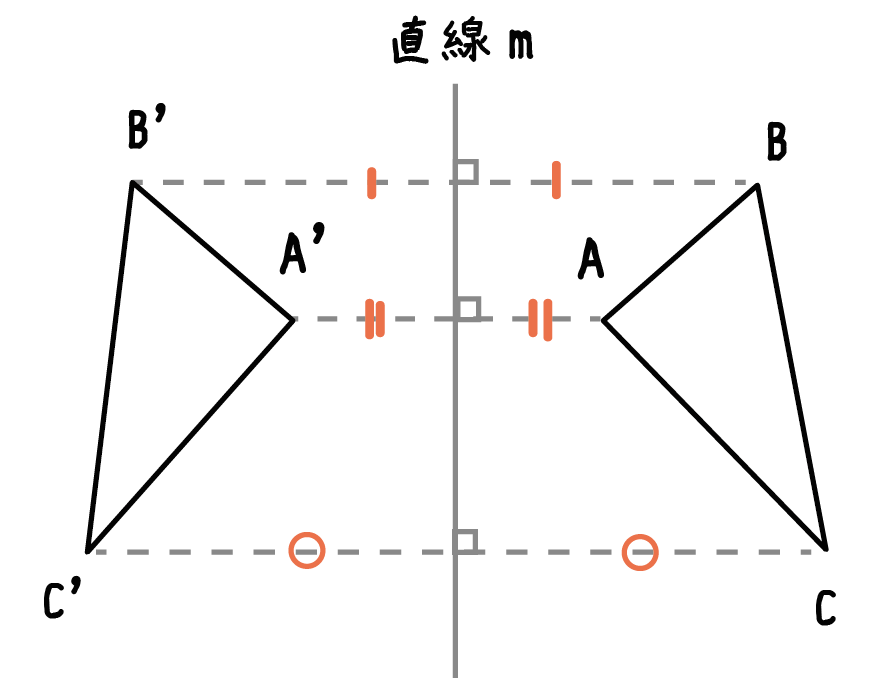
この対称移動の性質をおさえれば書き方もわかってくるよ!!
4つのステップでわかる!対称移動(線対称)の書き方
さっそく、線対称の書き方をさらっとみていこう。
Step1. ある頂点から「対称の軸」へ垂線をおろす
最初にやるべきことは、
対称移動させる図形の頂点を1つ選ぶことだ。
そして、
その頂点から「対称の軸」へテキトーに垂線をおろしてみよう!
さっきの例だったら、
点Aから直線mにこんな感じで垂線をひいてみるってこと↓↓
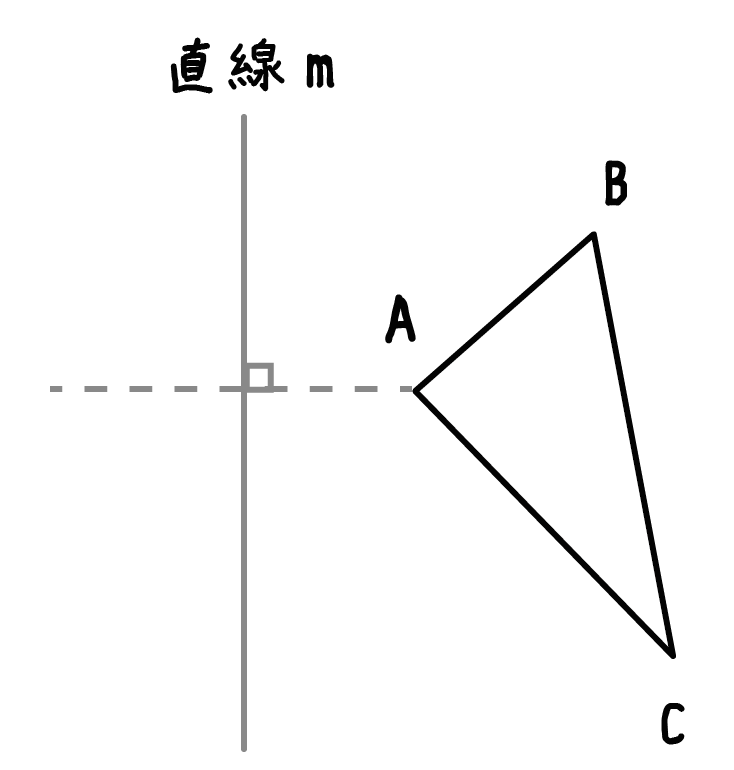
垂線をかくためには、
- 分度器
- コンパス
- 三角定規
っていう3つのアイテムのいずれかを使ってあげればいい。どれか好みのものをピックアップしてくれ!
Step 2. 「対称の軸」と「頂点」の距離を測る
つぎは、
「対称の軸」と「頂点」の距離を測ってあげよう。
線と点の距離は、
点から線におろした垂線の長さ
だったよね??
だから、これも同じ。垂線の長さをはかってあげよう。
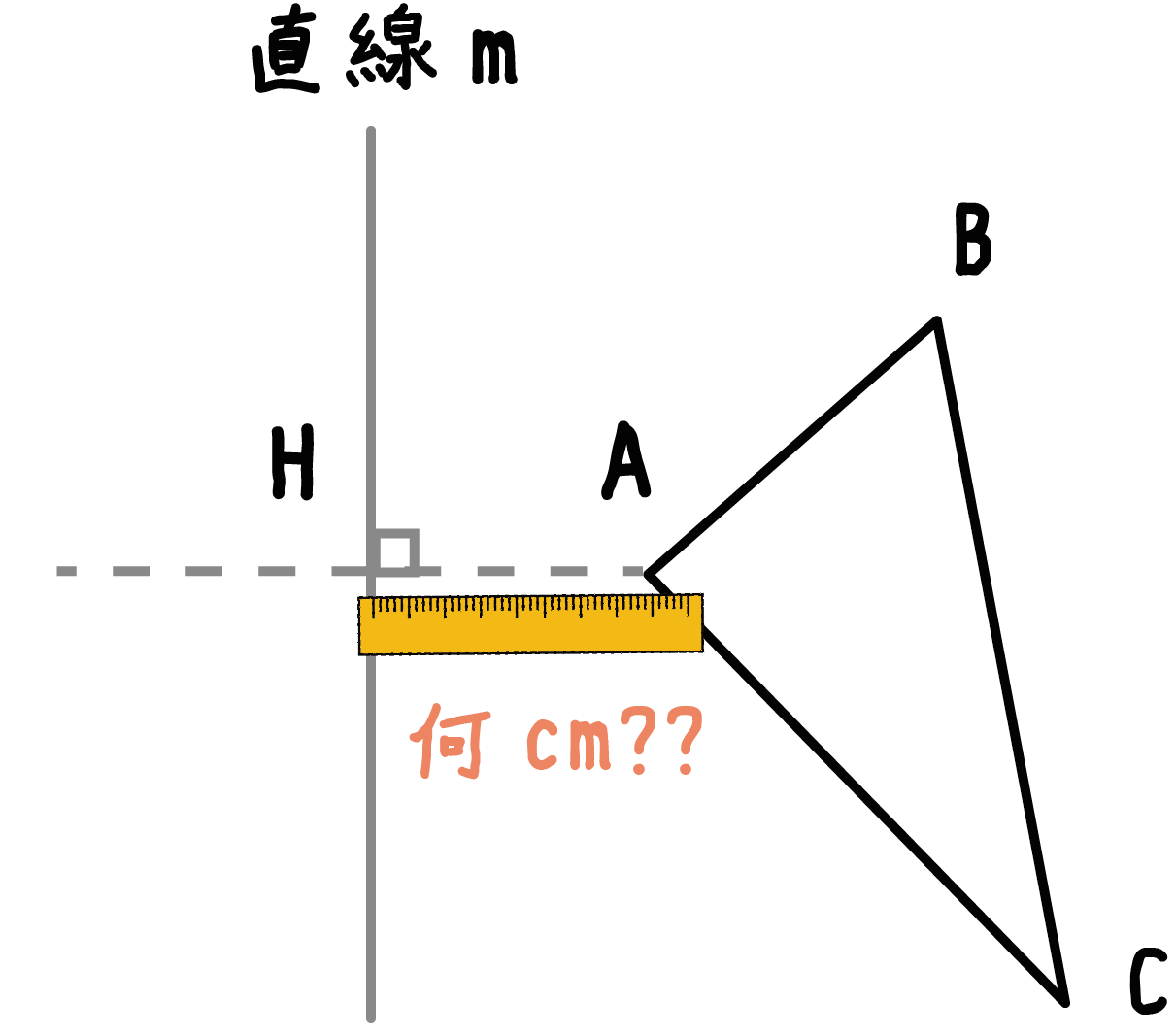
垂線と「対称の軸」の交点をHとしてやると、線分AHの長さがそれにあたる。
定規でも使ってAHの長さを測ってみよう!!
Step 3. 「対称の軸の向こう側に点をとる」
ステップ2でゲットしたつかった線分の長さを使うよ。
さっき測った線分の長さだけ、図形とは逆側の垂線上に点をうってやるんだ。
ちょっと言葉ではむずかしいので図をみてみよう。
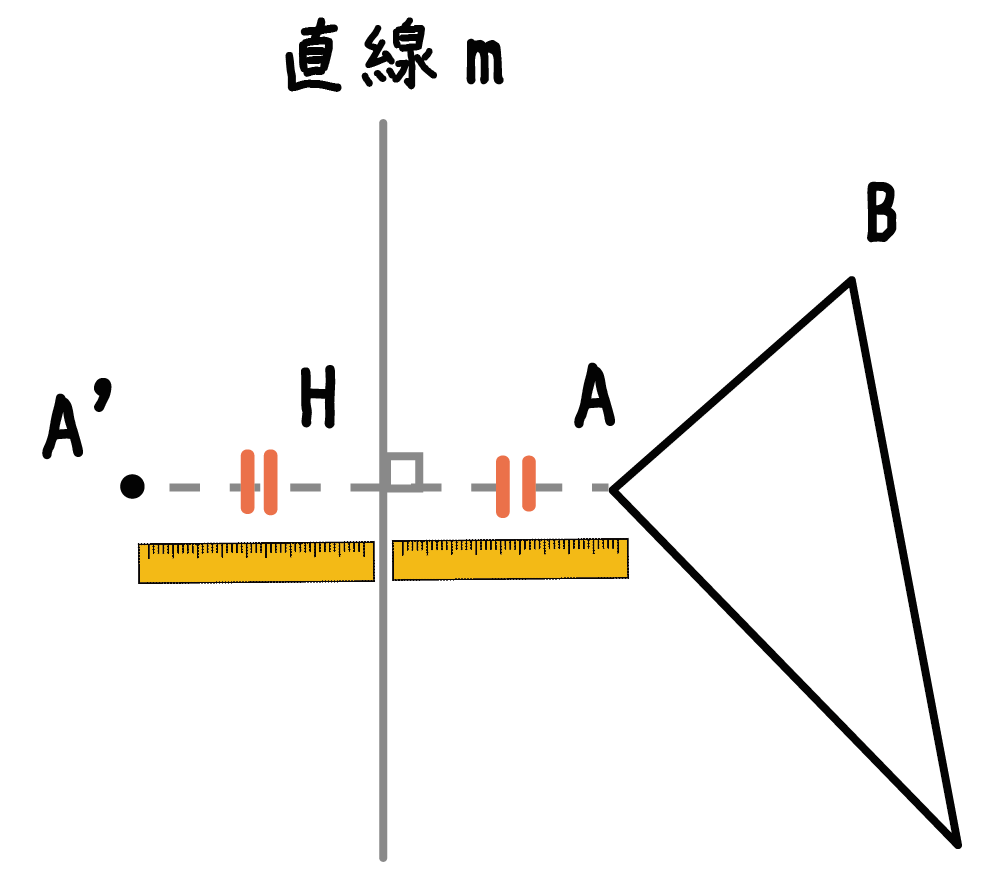
三角形ABCとは逆側に点A’をうつ。
そして、その点は垂線上に点Hから「さっき測った長さ分」はなれた位置だ。
コンパスでも定規でもいいから、必ずAHとA’Hの距離が等しくなるようにしよう!!
Step 4. 「1~3の手順を他の頂点でもくり返す」
あとはここまでの手順を他の頂点でもくり返すだけ。
例題でいうと、点Bと点Cの場合だね。
すると、こんな感じで3つの点がうてるはずだ(点A’、点B’、点C’)↓↓
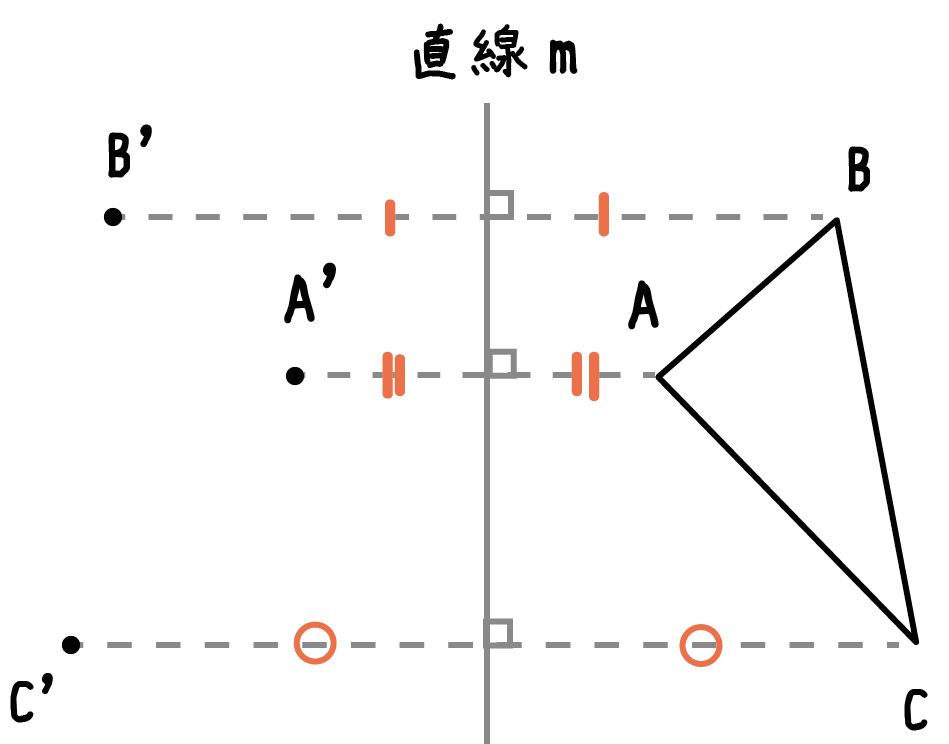
「対応する点」をすべて打てたらこっちのもの。
あとはこいつらを結んでやるだけさ。

これで対称移動(線対称)は完了だ。
書き方に4つもステップがあったけど、ゆっくりやれば間違えないはず!
まとめ:対称移動(線対称)の書き方は4つのステップしかない
以上が対称移動の書き方だ。
これでやっと、
っていう3つの図形移動をマスターできたね。
次回はちょっとややこしい「線対称と点対称の違い」について解説していく。よかったら確認してみてね。
そんじゃねー!
Ken


