【基本の作図】5ステップでわかる!平行移動の書き方
平行移動の書き方・作図がよくわからない??
こんにちは、この記事を書いているKenだよ。メガネふきが欲しいね。
「図形移動」の方法って次の3つあったよね。
- 平行移動
- 回転移動
- 対称移動
こいつらを「【中1数学】平面図形で勉強する「図形の移動」3つのまとめ」でだいたい確認してきたけれど、図形の移動を知っているだけじゃ問題は解けない。
じつは、
作図方法を知っていないとテストで点数はとれないんだ。

だから今日は、
平行移動の書き方・作図
をわかりやすく3つのステップで解説していくね。テスト前に参考にしてみてね。
~もくじ~
- 平行移動の作図でつかう1つのこと
- 平行移動の書き方4つのステップ
図形の平行移動のためには何が必要なの??
平行移動のために使うことはたった1つ。
それは、
平行移動した図形の性質だ。
平行移動した図形同士には、
対応する点を結んだ線分は、それぞれ平行で、その長さは等しい
という性質があるね。これは教科書にのっていることだ。
たとえば、三角形ABCを平行移動させたとすれば、
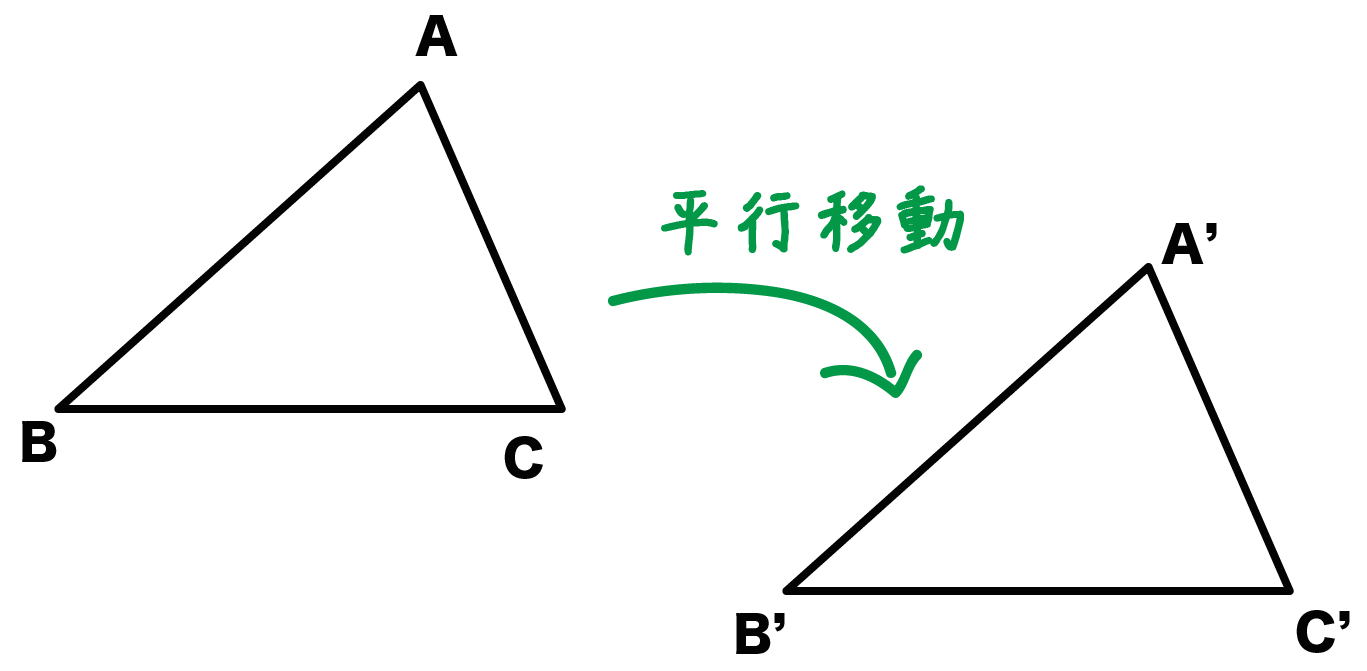
対応する点同士である、
- AとA’
- BとB’
- CとC’
を結んだ線分たちは、
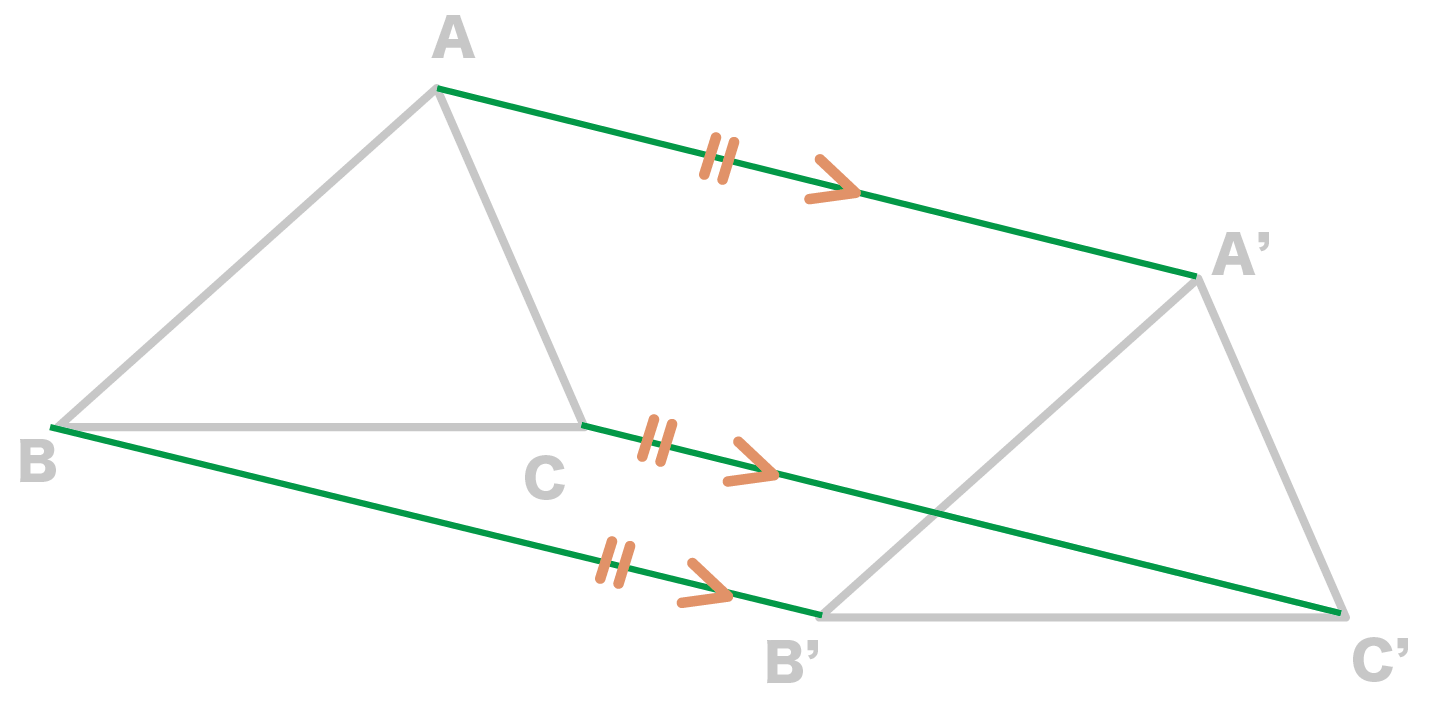
- たがいに平行
- 長さが等しい
という性質があるんだ。
これをつかえば作図がつぎの5ステップでできるよ。
平行移動の書き方・作図の5つのステップ
つぎのような作図問題が出されたとしよう。
問題:三角形ABCの頂点Aを点Pに移すように平行移動した図をかいてね。
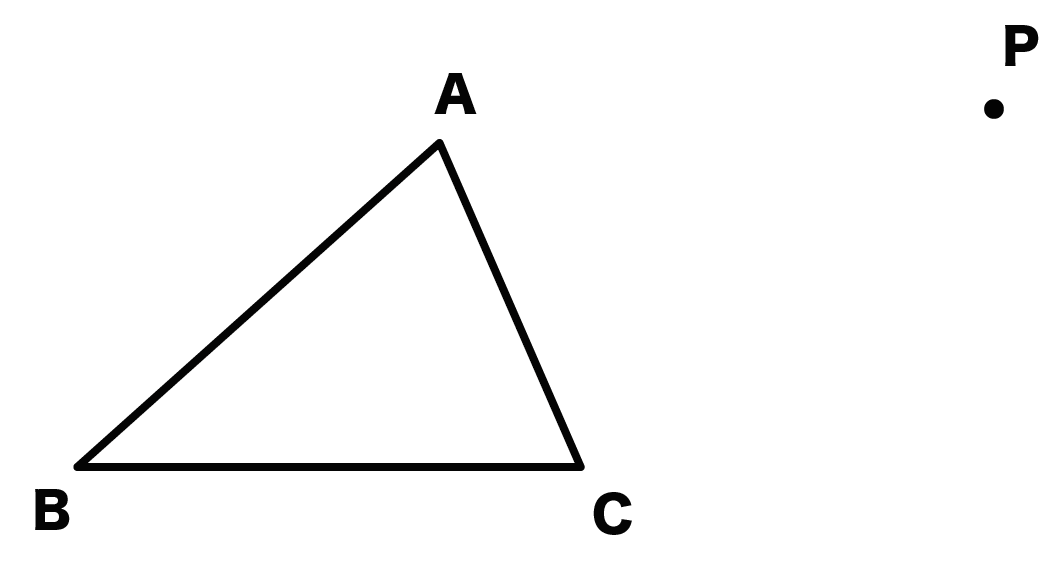
これをもとにしながら平行移動の書き方を解説してくね。
Step1. 対応する点同士をむすぶ。
まず、対応する2つの点を結んでしまおう!
ここでいう「対応する点」とは、
「移動する前の点」と「移動後の点」
のことだ。さっきの問題でいうと、点Aと点Pがそれにあたるね。
ってなわけで、
対応する点AとPをむすんで線分APをつくっちゃおう!
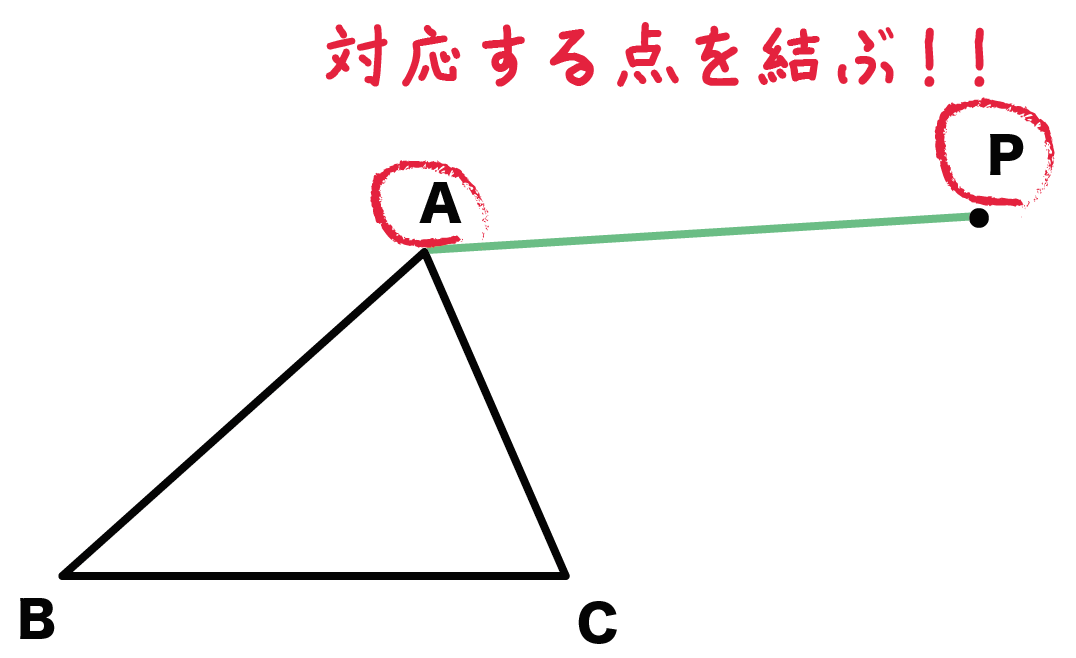
これが平行移動の作図の第一ステップさ。
Step 2. 各頂点から平行線をひく!
次に、さっき引いた線分の平行線を残りの頂点からひいてあげよう!
この問題では点BとCから線分APとの平行線をひくってことだね。
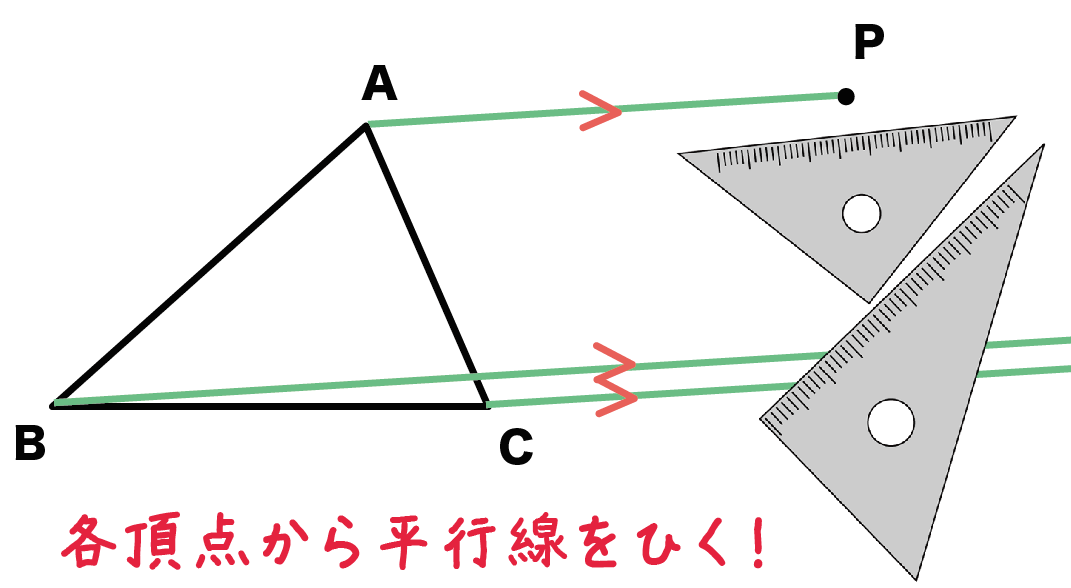
平行線をひくときはコンパスでも三角定規でもかまわない。
ただ、勘やひらめきで平行線をかかないようにしよう。
>>平行線の書き方はコチラ!!
Step 3. できた線分の長さをはかる!!
つぎに、対応する点を両端とする「線分の長さ」をはかろう!!
ここでは線分APの長さってことだね。
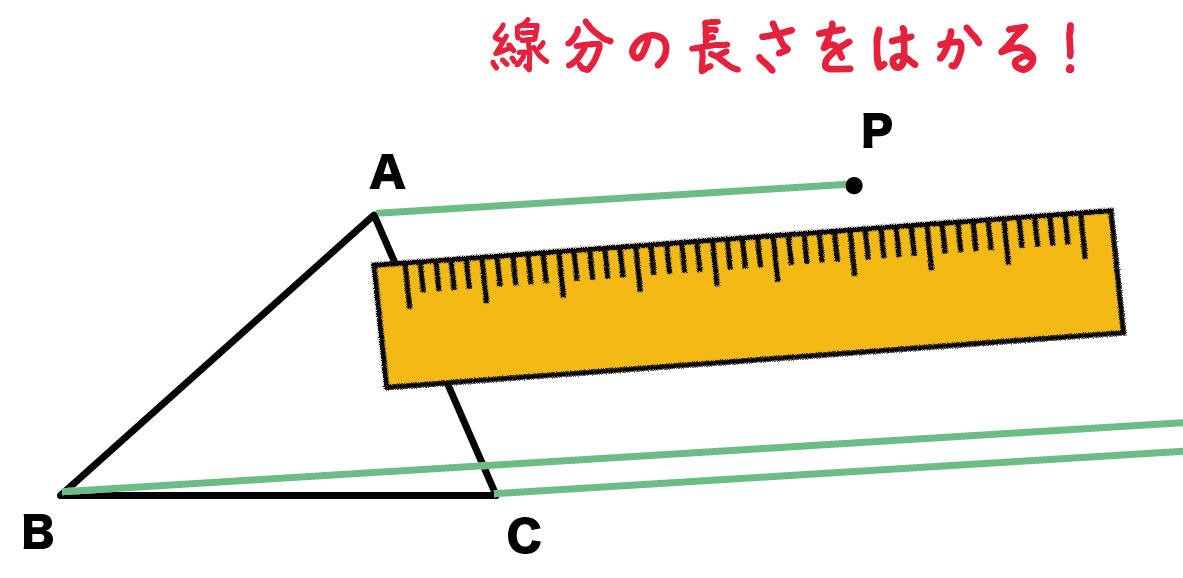
新しくできた線分に定規をあてるだけ。ゆっくり落ち着いてね。
Step 4. 同じ長さのところに新しい点をうつ
ステップ3で測った長さを使うよ。
平行線上に、各頂点からその長さ分はなれたところに点をうつんだ。ちょっと言葉じゃ説明しずらいから下の図をみてくれ。
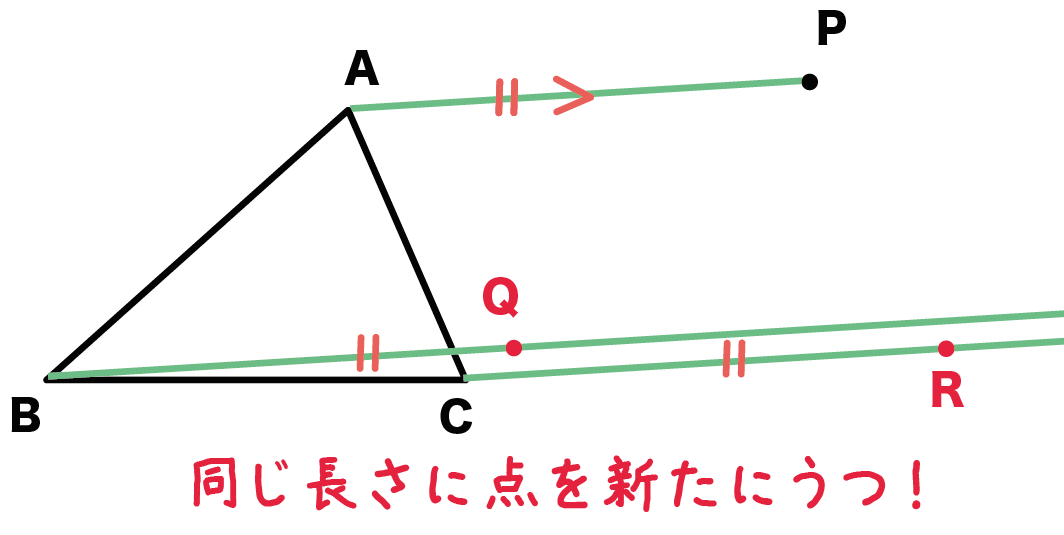
つまり、
AP = BQ = CR
となる新しい点Q・点Rを2つの平行線上にうつんだ。
これが第四ステップ。あと1つだね。
Step 5. 新しい点たちを結ぶ
最後のステップはとってもカンタン。
ステップ4まで苦労して打ってきた点同士を結ぶだけだ。
さっきの例でいうと、
- 点Q
- 点R
だね。そんで、点Pはもともと問題であたえられていた移動後の頂点。
だからこれも結んであげる。
そうすると、
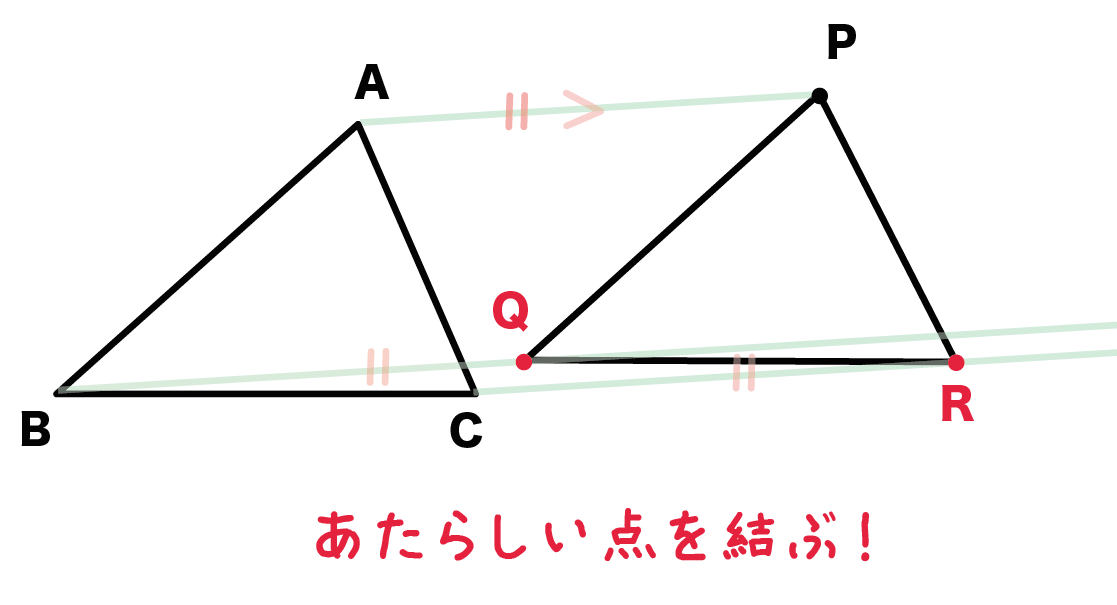
こんな感じで、
平行移動した三角形PQRが書けるんだ。
案外、平行移動の作図もカンタンそうでしょ!??
まとめ:平行移動の作図は5つのステップで書ける
ここまでみてきた平行移動の作図はどうだった??
5つのステップでゆっくりかけば大丈夫。
あせって間違えるより確実に問題に答えたいね。
つぎは「回転移動の作図」について解説してくねー!
そんじゃねー
Ken


