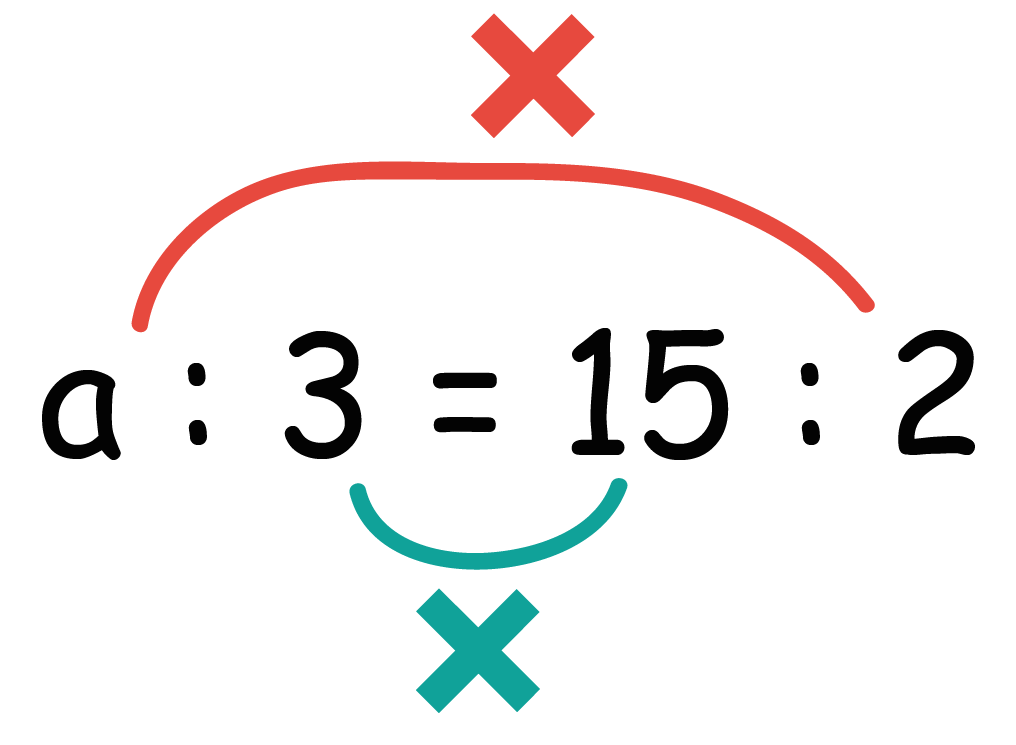【比例式の性質】3分でわかる!比例式の解き方
比例式の解き方はシンプル?! 比例式の性質さえわかればOK!??
こんにちは、マラソン好きのKenだよ。
比例式っていったい何のことだっけ?? 比例式とは下のような
2つの比が等しいですよ、
a :b = c : d
ということを表した等式のことだったよね。
それで、どういうときに2つの比が等しいっていえるかっていうと、
比の値が等しいとき
なんだ。
前回の「比の値」の記事で勉強した通り、左辺の「a:b」の比の値は「a/b」、右辺の「c : d」比の値は「c/d」になるよね??
そんで、 「a: b = c:d」となるときは2つの比の値が等しいことを意味するんだ。
今日は、比例式の解き方を「比例式の性質」を使って勉強してみよう!!
比例式を解くために必要な「比例式の性質」ってなに??
比例式の解き方に役に立つのは「比例式の性質」だよ。
教科書には、
a: b = c:d ならば ad = bc

ってことが比例式の性質って書いてあるでしょ??
えっ。なんで急に「比例式の性質」が成り立つなんて言えるのかって?!?
じつはこれは比例式の意味を使っているだけなんだ。
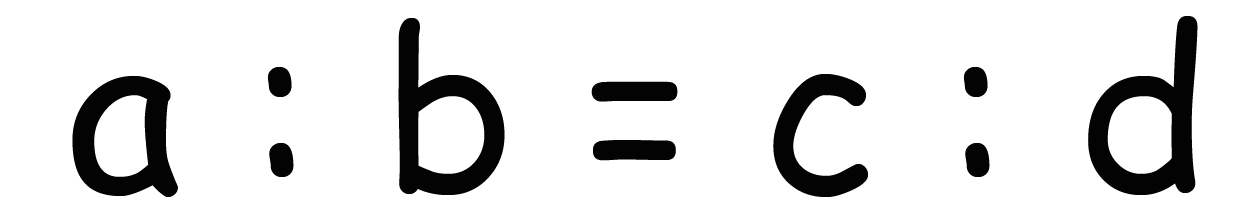
という比例式が成り立つとき、
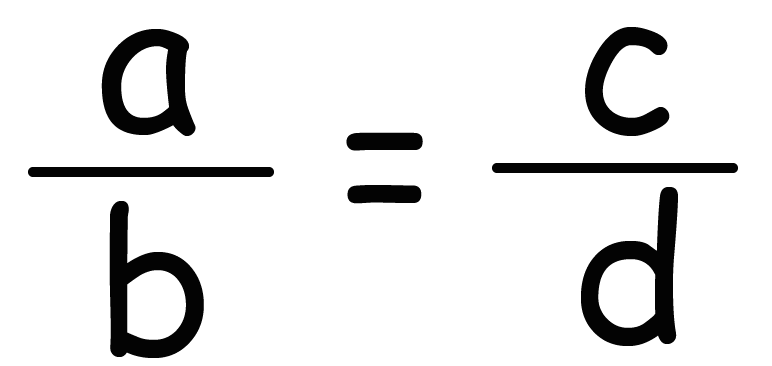
ということが言えたよね? これは一番はじめに説明したね。
じゃあ、気分転換にこの等式から分数をなくしてみよう! よくわからなかったら、「分数をふくむ方程式の解き方」を参考にしてみてね。
分母をはらうために両辺に「bd」をかけてやると、
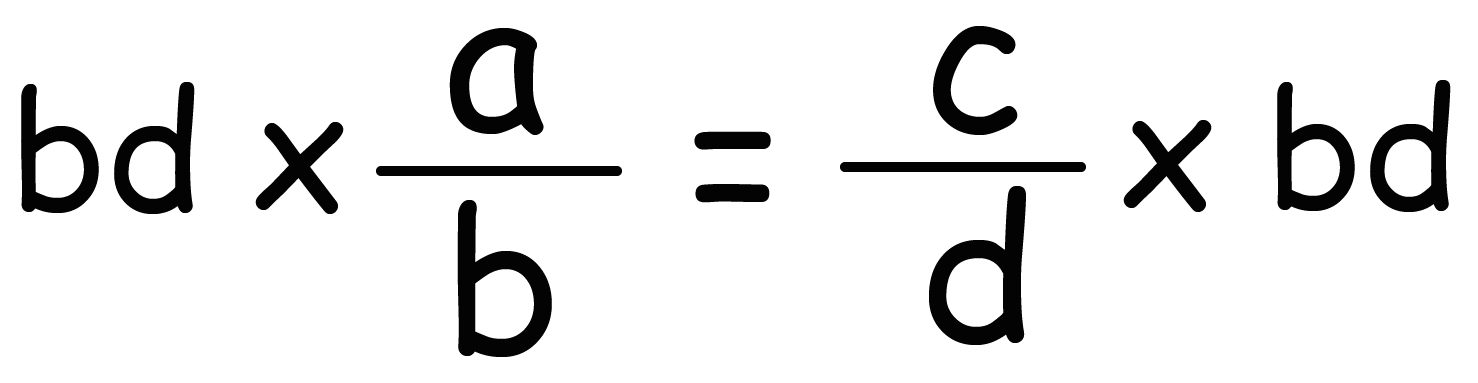
分母が消えて、
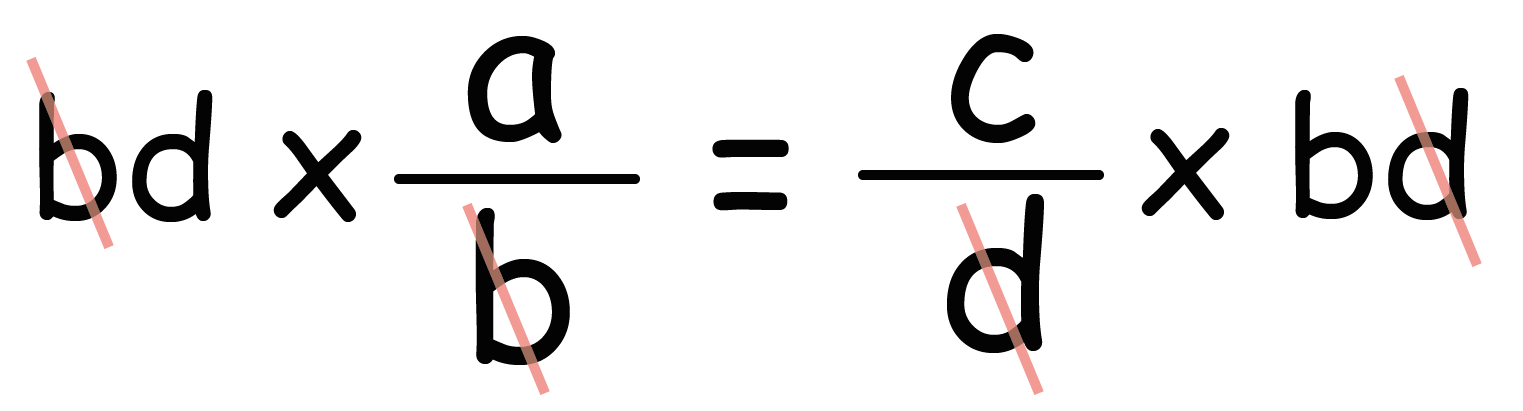
さっき紹介した「比例式の性質」の右側の等式の、
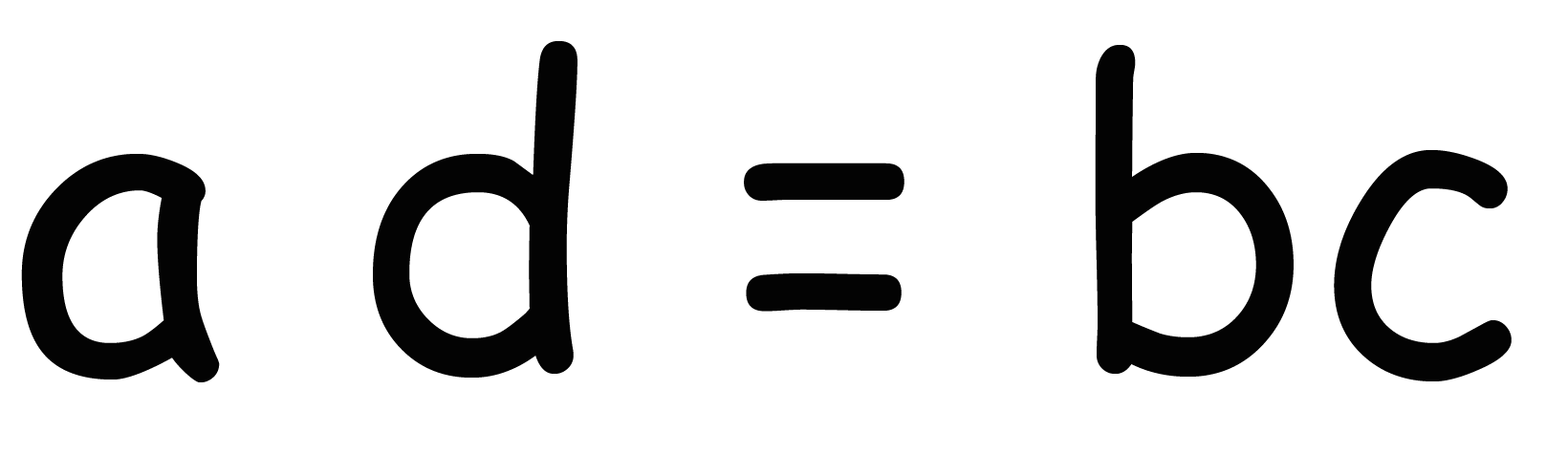
ad = cd
になるね。だから比例式の性質、
が成り立つんだね。
そして、
比例式の性質はあたかも「比の外側同士」「比の内側同士」の項をかけてるようにみえるよね??
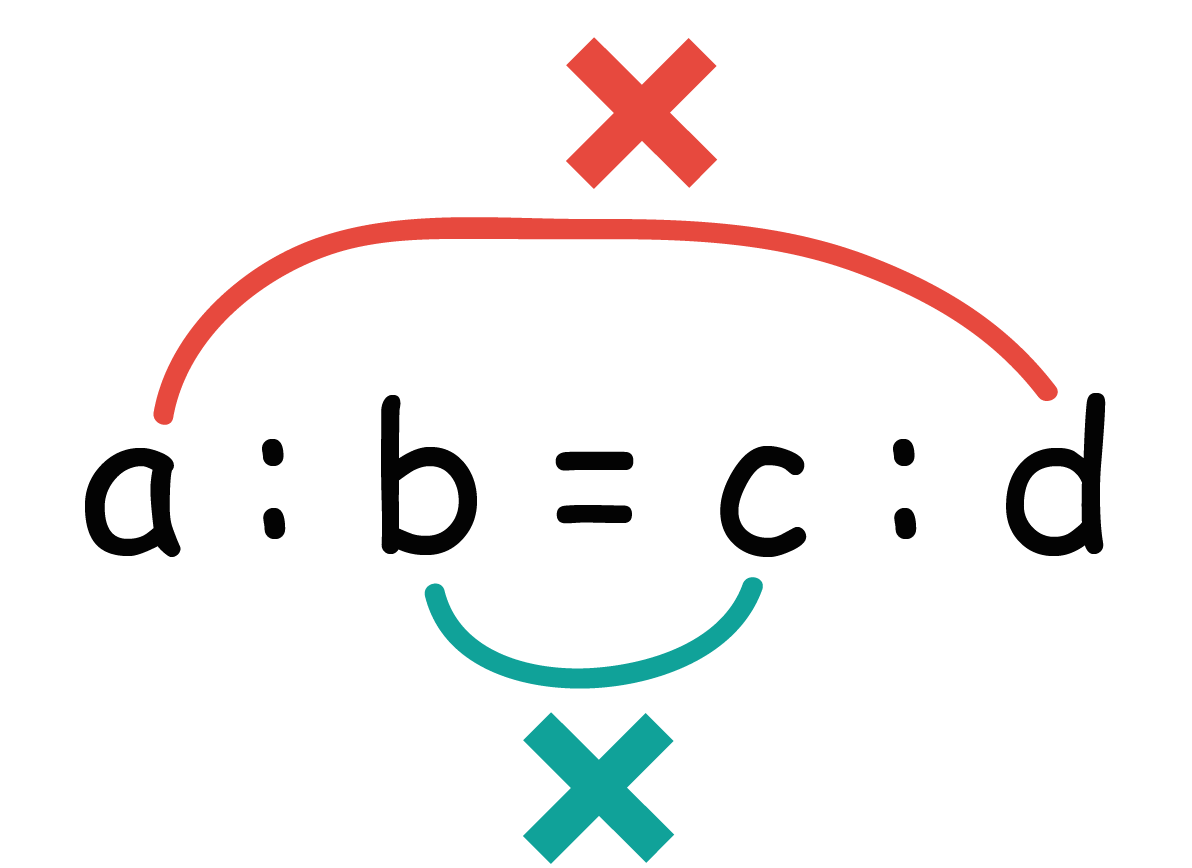
だから、ちまたでは「比例式の性質」のことを、
外項の積・内項の積
って呼ぶことがあるんだ。しっかりとこの言葉も押さえておこう!!
比例式を解くってなに??
比例式の解き方はわかったね?? それじゃあ実際の例題で解き方を確認してみよう。
たとえば次のような比例式があったとする。
a: 3 = 15:2
比例式にふくまれる文字の正体をあばくこと。
これが「比例式を解く」ってことなんだ。
だから、この例の場合はaを求めることが「比例式を解く」ってことになる。
さっき勉強した「比例式の性質」を使うと、
外側同士の項、内側同士の項をかけたものが等しくなるんだから、
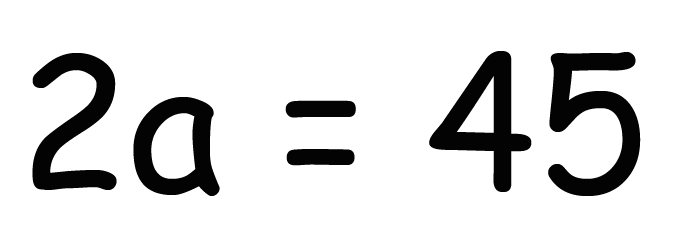
2a = 45になるね。
これをaについて解いてあげれば、
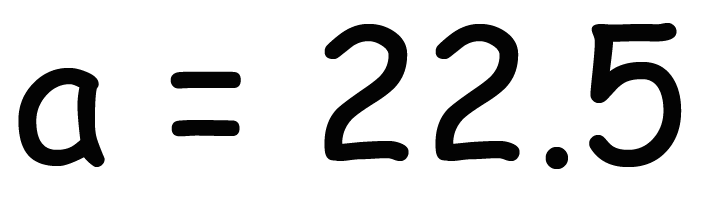
a = 22.5 (または45/2)になる。
どう?? 比例式の解き方も意外とシンプルでしょ??
次回はいよいよ、1次方程式の文章題のコツを解説していくねー!
そんじゃねー!
Ken