こんにちは!この記事をかいてるKenだよ。朗読をはじめたね。
平方根の計算でよくつかうのは、
ルートを簡単にする方法
だ。
ぶっちゃけ簡単にしなくてもいいんだけど、計算しやすくなるんだ。
しかも、先生によってはルートが簡単じゃないと×にするから要注意。
そこで今日は、
平方根(ルート)を簡単にする方法
を解説していくよ。
よかったら参考にしてみて。
= もくじ =
「ルートを簡単にする」とはずばり、
ルートの中身から整数を取り出すこと
なんだ。
たとえば、
√(aの2乗×b)
があったとしよう。
ルートを簡単にするってようは、
中身の「aの2乗」をルートの外に出すことなんだ。
aの2乗をルートの外にだしてやると、
√(aの2乗×b)= a√b
になるね。
なぜなら、
√(aの2乗×b)
= √(aの2乗)× √b
= a×√b
= a√b
になるからさ。
ルートを簡単にする方法はたったの3ステップ。
例題をいっしょにといてみよう。
例題
つぎの平方根たちの中身をできるだけ簡単にしてください。
(1 ) ルート12 (2) ルート112 (3)ルート180
ルートの中身を素因数分解してみよう。
えっ。
素因数分解なんて忘れたって?!
そういうときは、素因数分解のやり方をよんでみて。
例題も素因数分解してみよう。
の根号のなかにはいってるのは、
たちだね。
こいつらを素因数分解してやると、
になる。
ルートの中から、
2乗になっている因数
をみつけよう。
例題の平方根たちをみてみると、
ってかんじで、ちらほらと2乗の因数がみつかったね。
えっ。
112みたいに4乗になっている因数がある??
そういうときは、それを「2乗した数」の2乗になっていると解釈しよう。
最後に、2乗の因数を√の外にだそう。
例題でも、2乗になってる因数をとりだすと、
になるね!
平方根を簡単にする方法はどうだった??
の3ステップで攻略できちゃうよ。
えっ、もっと高速にルートを簡単にしたい??
そんな君のために、ルートを簡単にする電卓アプリ「Simproot」をつくったよ。
よかったら試してみて。
ルートをどんどん簡単にしてこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。血糖値は高いね。
平方根をみていると、
どれくらいの大きさなんだろうな・・?
って思うことあるよね。
ルート!ルート!
っていわれてもデカさわからんし。
たとえば、ある少年に、
19万円ほしい
っていわれたら、大きい金額であるし、慎重になるじゃん??
でもさ、
ルート19万円ほしい
っていわれてもピンとこないよね??。
高いのか低いのか検討もつかん。
今日はそんな事態に備えて、
平方根のだいたいの値の求め方を勉強していこう。
この「だいたいの値」のことを、
数学では「近似値」とよんでいるんだ。
平方根の近似値を求め方では、
大きな数であてをつけて、じょじょに範囲をせばめていく
っていう手法をつかうよ。
だから、まずは、
その平方根がどの整数の範囲におさまっているのか??
を調べる必要があるんだ。
さっきでてきた、
√19万円
がだいたい何万円になっているのか??
を調べていこう!
まずは、
平方根がどの整数と整数の間にあるのか??
のあてをつけよう。
あての付け方としては、
2乗をしたときに√の中身をこえてしまう整数
と
ギリギリこえない整数
をだせばいいんだ。
√19で考えてみよう。
整数を1から順番に2乗してみると、
・・・・・・・
になるね。
どうやら、「19」は、
のあいだにありそうだね。
よって、√19は、
4 < √19 < 5
の範囲におさまってるはず!
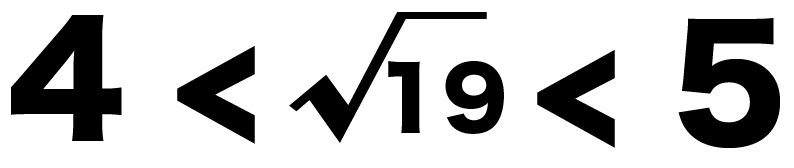
つまり、
√19の1の位は「4」ってわけだね。
ふう!
近似値の1の位はわかったね??
おなじことを小数第1位でもやろう。
「√19」の1の位は4だったね??
今度は、小数第一位の数字を1から順番に大きくしていこう。
んで、
2乗して19をこえるポイントをみつければいいんだ。
・・・・
ぬぬ!
19は、どうやら、
のあいだにありそうだね。

ってことは、√19の範囲は、
4.3 < √19 < 4.4
になるはずだ。
だから、√19の小数第1位は「3」になるはずだね。
最後もやり方はおなじ。
小数第2位を1から順番に増やして2乗。
ルートの中身を超えるポイントをみつければいいんだ。
√19でも小数第2位のあてをつけよう!
小数第1位は「3」だったよね??
だから、調べるのは4.31からだ。
0.01ずつたして、そいつらを2乗していこう!
おっと!
4.36の2乗で19をこえちゃったね。
ってことは、19は、
の間にあるはずなんだ。
つまり、
4.35 <√19 < 4.36
になってるね!
ってことは、
√19の小数第2位は「5」になるはず!
やったね!
この「4.35」が√19の小数第2位の近似値だよ。
あの少年は4.35万円、つまり、4万3500円ぐらいを請求していただわけだね。
まったく、可愛いけど憎いやつだ。
こんな感じで、
1の位からじょじょに範囲をせばめていこう!
平方根の近似値があってるか確認してみて。
計算機の√ボタンをおしてやれば・・・・ほら!
一発で平方根の近似値がだせるんだ。
たくさんのケタ数をね。
うん!
たしかにあってる!
√19の小数第2位は「5」だもんね。
計算機で確認できるから便利だ。
平方根の近似値の求め方はシンプル。
1の位からじょじょに範囲をせばめればいいんだ。
池の魚をおいつめるみたいだね。
計算は大変だけど、気合と根性でせばめていこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenです。レモンは皮がうまいね。
ルートの問題でよくでてくるのは、
平方根の大小
の問題だ。
ようは、
整数や平方根をみくらべて、どっちのほうがデカいのか??
をあてる問題だ。
はじめてだと大小をくらべるのはムズいよね。
わかるよ、その気持ち。
でもじつは、
平方根の大小の問題はシンプルなんだ。
なぜなら、問題の種類をたった2タイプにわけられるからね。
この2つさえマスターすればこっちのもの。
今日は、この2つの問題をくわしくみていこう!!
まずは、
平方根と平方根の大小をくらべる問題
だ。
たとえば、つぎのような問題だね↓↓
例題
つぎの2つの平方根の大小を不等号をつかってあらわしなさい。

解き方はちょー簡単。
ルートをとっぱらって大小をくらべればいい
のさ。
さっきの例題をみてみて。
をくらべるのはむずいね??
だから、思い切って√をとって、中身の、
の大小をくらべるんだ。
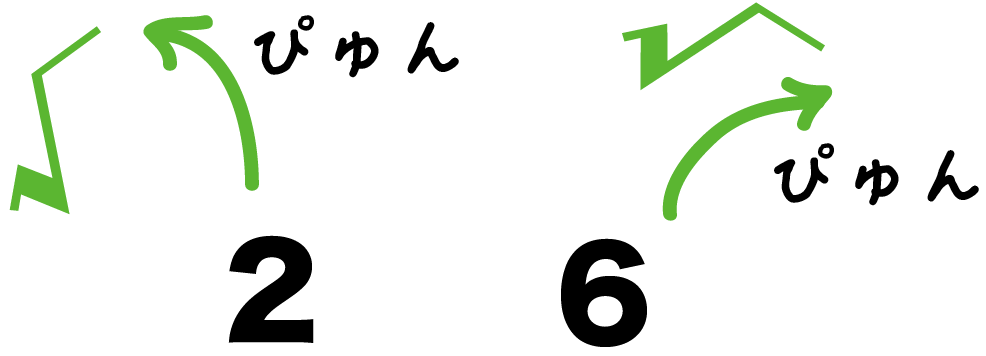
2と6をくらべると、
あきらかに6が大きいよね??
だから、√をつけても√6のほうが大きいのさ。
えっ。なぜこんなことがまかり通るのかって!??
じつは、平方根には、
√の中身が大きいほど絶対値が大きくなる
っていう性質があるからなんだ。
だから、√2よりも√6が大きいし、
√10なんてもっと大きい。
逆に負の平方根でいうと、
-√2より-√6のほうが小さいし、-√10なんてもっと小さい。
なぜなら、
負の数では絶対値が大きいほど小さくなるからね。
こんな感じで、平方根同士の大小をくらべるときは、
√の中身と符号で判断しよう!
つぎは「整数」と「平方根」をくらべる問題。
たとえば、つぎみたいなヤツだね ↓↓
例題
つぎの4つの数字の大小を不等号をつかってあらわしなさい。
このタイプの問題は、さっきよりもヤッカイ。
なぜなら、
整数を平方根になおす
必要があるからね。
整数と平方根同士をくらべるのはむずい。
だから、
整数を平方根にしてやって、
平方根同士をくらべる路線にもっていくんだ。
例題で整数なのは、
の2つ。
こいつらを平方根であらわしてみよう!
えっ。平方根になおす方法がわからないだって?!?
やり方は簡単。
あえて2乗してルートのなかにぶちこめばいいんだ。
だから、
はそれぞれ、
の平方根に置き換えられるわけさ。
こんな感じで、ぜーんぶ平方根になおせば一件落着。
さっきの「平方根同士の大小の解き方」でとけちゃうよね。
小さい順にならべてみると、
-√16, -√10, √5, √9
になるね。
んで、
さっき平方根にした整数をもとにもどすと、
-4, -√10, √5, 3
になるはずだ!
ついでに不等号であらわすと、
-4 < -√10 < √5 < 3
になるね。
おめでとう!
どんな大小でもバッチコイだ!
平方根の大小の問題??
やばそうにきこえるけど、意外に簡単。
の2種類しかないからね。
平方根同士だったらルートを無視。
整数は平方根になおしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。スタミナを補給したね。
平方根の求め方にはいろいろある。
小数の平方根の求め方、
分数の平方根の出し方、
平方根を簡単にする方法・・・・
などなど。
まさに多種多様。
混乱しちゃうかもしれないね。
そこで今日は、
超基本的な平方根の求め方を解説していくよ。
いちばん簡単な求め方だから、
ガッツリおさえちゃおう!
平方根の出し方を紹介するよ。
3ステップで求められちゃうんだ。
つぎの問題をといてみよう!
例題
つぎの数の平方根を求めなさい。
7, 9
元の数にルートをかぶせよう。
そう、
√
をね。
ぱさっとね、上からかければいいんだ。
さっきの例題では、
の平方根を求めるんだったね??
だから、こいつらの上に「√」をかぶせればいいのさ。
帽子みたいにね。
そうすると、
になるはずだ!!
つぎは、
±(プラスマイナス)
をつけてやろう。
文字通り、
プラスとマイナスが合体した記号
だ。
平方根にはプラスとマイナスのものがあって、
どちらも絶対値が等しい。
だから、
プラスマイナスで1つにまとめられるんだ。
※くわしくは平方根の性質をよんでみてね。
例題でも、さっきルートをつけた、
に±(プラスマイナス)をつけよう。
付け方はくそ簡単。
ふつーに左にチョコっとくっつけるんだ。
そうすると、
になるよね。
せっかくルートをつけたんだけど、
ルートをもう一回はずせるかチャレンジしてみよう。
ルートをはずせる条件は1つ。
それは、
ルートの中身が「○○の2乗」になっていればいいんだ。
条件にあてはまるなら、
2乗とルートをとっていいんだ。
たとえば、±ルートaの2乗だったら、±aになるってわけさ!
例題を振り返ってみよう。
まず、±√7だ。
ルートの中身は7だね。
この中身の7は・・・・うーん、どうやっても、○○の2乗の形になおせない。
だって、2回かけて7になる整数なんてないし・・・!
だから、
±√7は±√7でいいわけだ。
あともう1つの±√9。
こいつはルートをはずせそうだ。
なぜなら、
ルートの中身の「9」が「3の2乗」になってるからね!
√をとってやると、
±√9 = ±3
になるってわけさ。
よって、
7と9の平方根は、
の2つだ。
これで平方根の求め方もマスターだ!^-^
平方根の求め方はむちゃくちゃ簡単。
ルートをかぶせて、±を左にくっつける。
最後にルートをはずせるかトライするだけ。
ガンガン平方根を求めていこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。窒素より酸素だね。
平方根の正体はなんとなくわかった。
じゃあつぎは、
平方根にはどんな性質があるのか??
をみていこう!
性質までおさえればこっちのもんさ。
平方根の性質には2つあるよ。
ある正の数の平方根は、
ってやつさ。
ちょっとよくわからないから、くわしくみていこう。
ある正の数の平方根には、
「プラス」と「マイナス」のやつ
が1つずつ存在してるんだ。

だから、2つの平方根が「プラス」ってわけでもないし、
平方根が「3つ」できたりもしない。
あくまでも、
「符号違い」
で、
平方根が「2つ」でてくる
ってことを覚えておこう!
たとえば、49の平方根を考えてみて。
「しちしちしじゅうく」だから、49の平方根は7になりそうだね。
あとは、7にマイナスをつけた「-7」も平方根だ。
なぜなら、負の数は2回かけるとプラスになるからね。
だから、「-7」も49の平方根になる。
こんな感じで、
プラスとマイナスの平方根がある
っておぼえておこう!
つぎは、平方根の絶対値に注目してみて。
ある正の数の平方根には、
絶対値が等しい
っていう性質があるよ。
49の平方根は、
の2つだったね??
さっきみたように、あきらかに符号がちがうね??
だけど、それと同時に、
絶対値がおなじ
ともいえるね。
なぜなら、2つの平方根の絶対値はそれぞれ、
だからね。
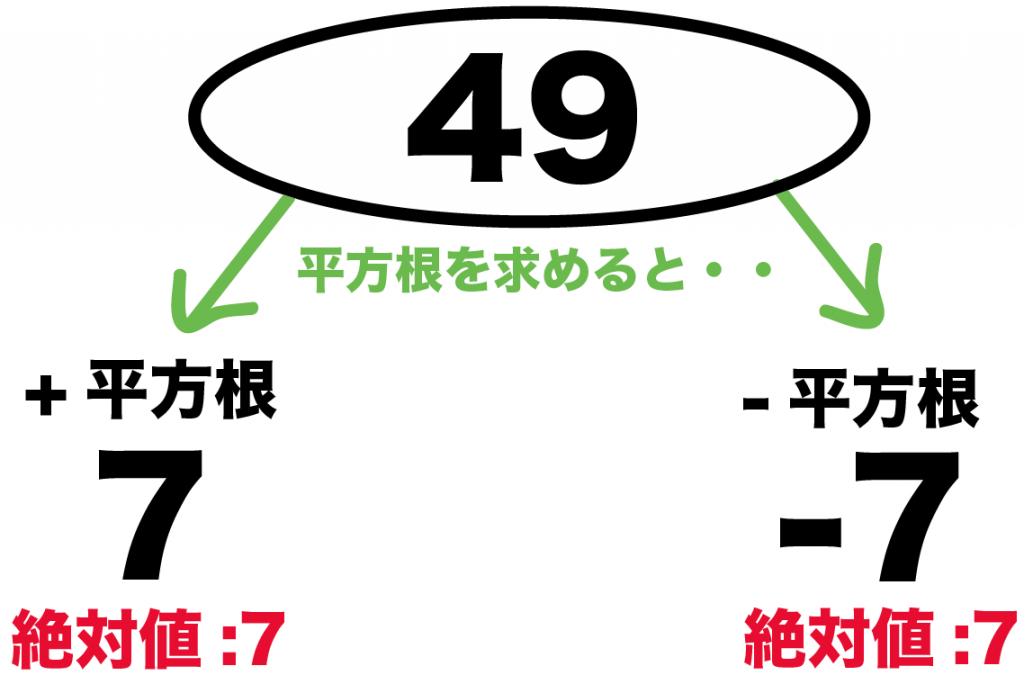
これが2つめの平方根の性質だ。
ある正の数の平方根には、
っていう性質がある。
こいつらをうまくつかうと、
2つの平方根を1つで表せるんだ。
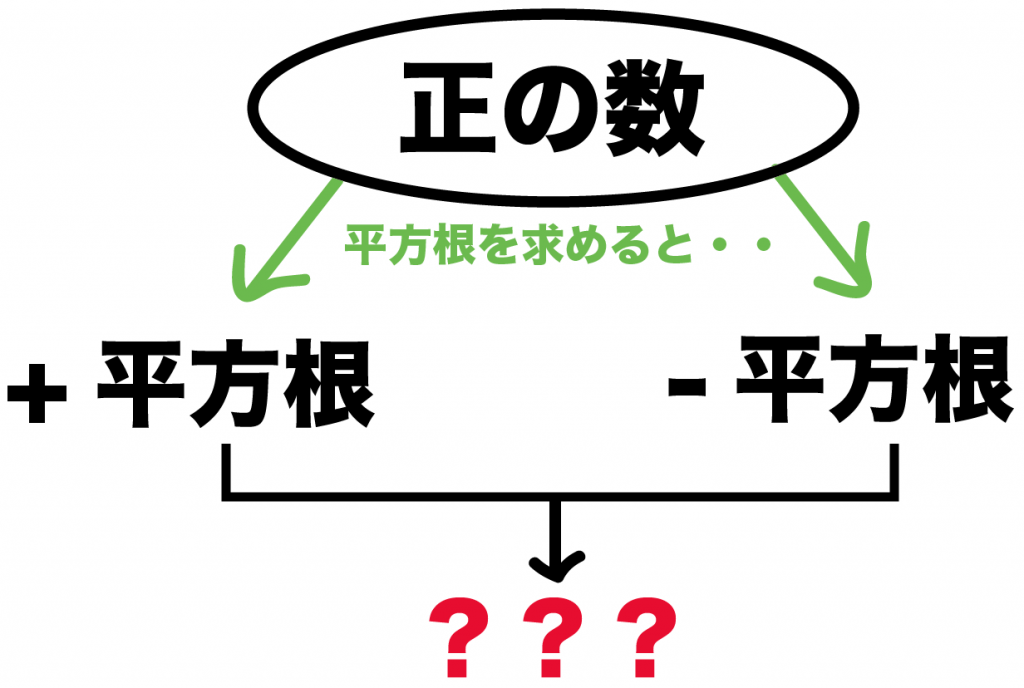
2つの平方根を1つの平方根であらわすには、
±(プラスマイナス)
っていう符号をつかうよ。

これはむちゃくちゃシンプルな記号。
上に「 +」、下に「-」がついてるから、正負の2パターンを同時に表現できるんだ。
プラスマイナスで平方根をあらわしてみると、
±平方根
になる。
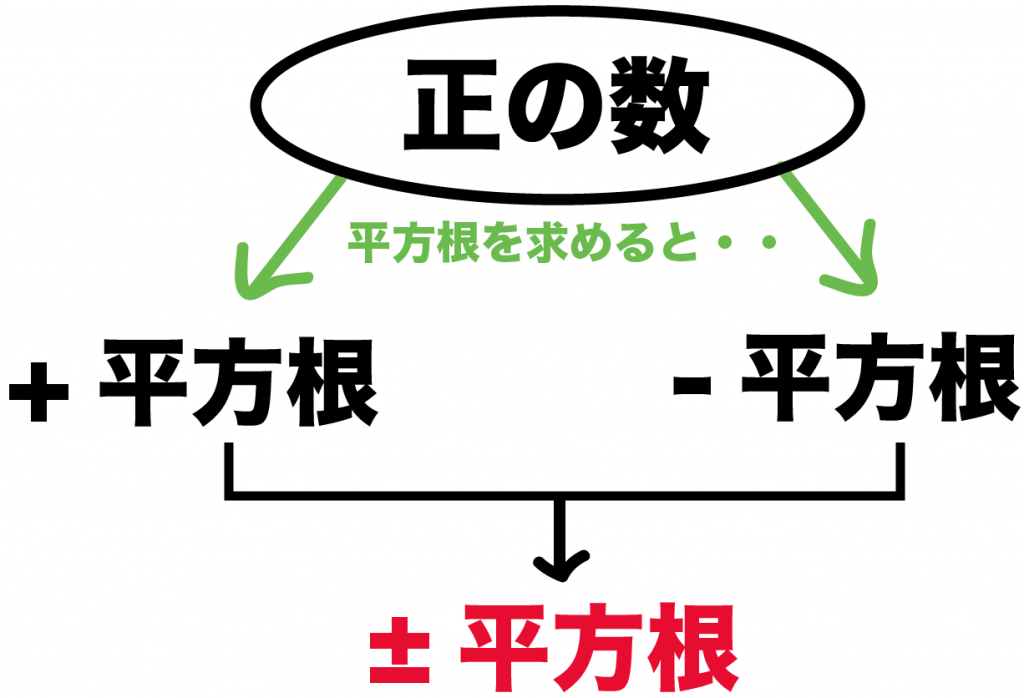
たとえば、49の平方根は、
の2つだったね??
こいつらをプラスマイナスで1つにすると、
±7
になるわけさ。
どう??
平方根の性質もしっくりしたかな??
平方根の性質には、
ってやつがある。
んで、
プラスマイナスをつかえば一気にあらわせるんだ。
これから平方根を勉強していくから、しっかり基本をおさえておこう。
そんじゃねー
Ken
こんにちは!この記事かいているKenだよ。鮭はたれが決め手だね。
中3数学になると、いきなり、突然、
√
っていう記号が出現するね。
はじめてみたときは、まじ意味不明。
ほかにも、わけのわからない、
平方根、ルート、根号・・・
みたいな用語がでてくる。
数学が苦手だったら、逃げ出したくなるね。
うん。まちがいない。
今日は苦手克服のためにも、
平方根・ルート(√)の意味とは???
を振り返ってみよう!
= もくじ =
まずは、
平方根(へいほうこん)の意味
だ。
漢字をちら見すると、
「根」
っていう漢字がみえるね。
漢字から推測しちゃうと、
大根や人参みたいな根菜の一種かと思うかもしれない。
だけどね、これは野菜、じゃない。
ある一種の数字のことなんだ。
えっ。もったいぶらずに早く言えだって??
そうだね。
じつは、平方根の意味とは、
2乗したら「ある数」になる数のこと
なんだ。
この数を「ある数」の平方根とよんでいるんだ。
たとえば、25の平方根を考えてみよう。
平方根を考えるときは、
なにを2乗したらその数になるんだっけ??
って考えてみればいいのさ。
えっと、、、、
2乗にしたら25になる数字かああー
うーん、ぬーん、
・・・・・
は!
5
だ!
だって、ごごにじゅうごだもんね。
5を2回かけたら25になるじゃん!!?
だから、25の平方根は5のはずだ!!
・・・・・・
ってかんじで平方根をみつけてみようw
あと、じつはね。
平方根にはプラスとマイナスの2パターンあるんだ。
だから、25の平方根は5のほかにも、
-5
があるよ。
なぜなら、-5を2回かけても25になるからね。

こんな感じで、
ある数の平方根は「+」と「-」の2通りある
っておぼえておこう。
⇒ 詳しくは平方根の性質をよんでみて
数学界には便利な記号がある。
それは、
√
ってやつだ。
名は、
根号(こんごう)
というんだ。英語っぽく読んでやると、
ルート
と発音するよ。
どっちかっていうと、
「ルート」って読むヤツの方が多いね。
ぶっちゃけ、
「根号」とよむやつはマイノリティ。
じゃあいったい、根号・ルートってなんなんだろうね??
こいつらは、
数字や文字にかぶせるだけで、平方根をつくれる記号
なんだ。
ちょっと特殊なマジックハットだと思ってもらえばいい。
ハリーポッターでいうと組み分け帽子みたいなもんだ。
たとえば、「正の数a」の平方根を√(ルート)であらわすと、
√a
と
-√a
になる。
なぜなら、
「√a」を2乗したらaになるし、
「-√a」を2乗してもaになるからね。
たとえば、さっきの例の25の平方根だったら、
の2つになるはず!
2回かけて25になる数は、
の2つだったよね??
つまり、
ってわけさ。
どう??
ルートってむちゃ便利でしょ!!?
かぶせるだけで平方根をつくれちゃうんだもん。
平方根は、
2乗したらある数になる数のこと
だったね??
んで、
かぶせるだけで平方根に変身させちゃう魔法のツールが、
ルート(根号)
ってわけだ。
平方根とかルートはたくさん登場してくる。
しっかり基礎をおさえておこう!
そんじゃねー
Ken