【連立方程式】食塩水の文章題を攻略する3つのステップ
連立方程式で食塩水問題を解けだって?? こんにちは!この記事をかいているKenだよ。水、うまいね。 連立方程式の文章題ってヤッカイだよね。 うん。 むちゃくちゃわるよ、その気持ち。 だけど、もっとメンドクサ…
 中2数学
中2数学
連立方程式で食塩水問題を解けだって?? こんにちは!この記事をかいているKenだよ。水、うまいね。 連立方程式の文章題ってヤッカイだよね。 うん。 むちゃくちゃわるよ、その気持ち。 だけど、もっとメンドクサ…
 中1数学
中1数学
食塩水の問題の解き方わからん! こんにちは!この記事をかいているKenだよ。バームクーヘンっておいしいね。 食塩水の文章問題が苦手な子って多いよね。 何を隠そう。 ぼくも中学生の頃、チョー苦手だったよ。 な…
 中2数学
中2数学
連立方程式の文章題の解き方がわからない!? こんにちは!この記事をかいているKenだよ。うなぎ好きだね。 連立方程式の文章題って苦手。 ふつうの計算ならできるんだけどなあ・・・・ って思ってない?? &nb…
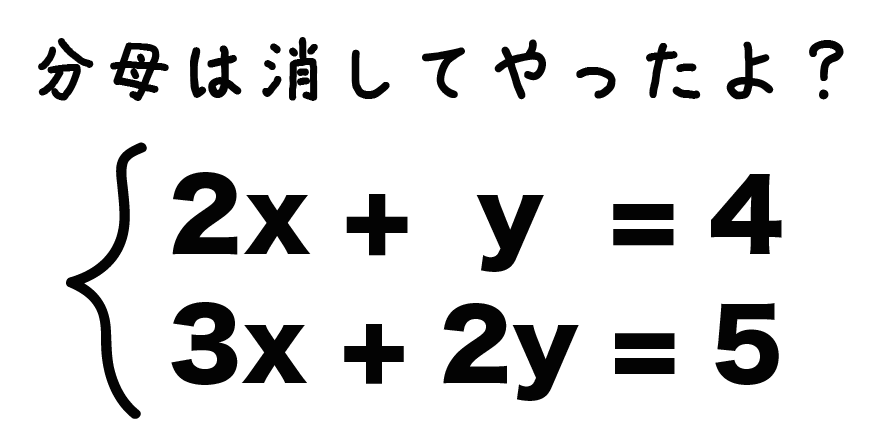 中2数学
中2数学
連立方程式に「分数」がいる?? こんにちは、この記事をかいているKenだよ。ジムに通い始めたね。 分数がはいっている連立方程式 って、たまにあるよね?? ↓ たとえばこんな感じ ↓ 例題 つぎの連立方程式を…
 中2数学
中2数学
連立方程式の加減法の解き方はムズい?? 連立方程式の加減法はチョー便利。 テストではだいたい「加減法」を使うからね! 「代入法」を使うのは結構だるいんだよ。 「加減法」なら楽できるってわけさ。…
 中2数学
中2数学
連立方程式の解き方の解説がほしい! こんにちは!この記事をかいているKenだよ。昼寝は好きだね。 連立方程式ってムズいよね。 加減法や代入法とかあるし、 方程式も2つあるからクラクラしてこない?。 今日はそ…
 中2数学
中2数学
連立方程式の解き方はよくわからん!? 連立方程式の解き方には2つある。 それは、 加減法 代入法 だったね。 連立方程式の解き方が2つもあって便利・・・ って思うじゃん?。 だけれども、 「加…