こんにちは、Drリードだよ。
ここまで相似な図形を勉強してきたよね。
相似の記号もおぼえたし、
相似比も求められるようになった。

今日はね、もう一歩踏み込んで、
相似な図形同士がもつ性質を勉強していこう。
相似な図形たちはどんな性質をもっているんだろう??
さっそく相似な図形の性質を紹介しよう。
つぎの性質があるんだ。
つぎの△ABCを想像してみて。
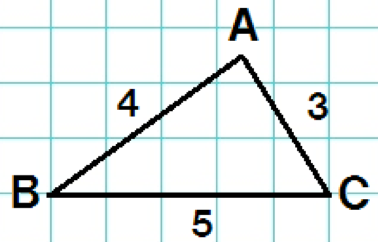
こいつを2倍に拡大してみよう。
スマホやタブレットの画面で、
「ピンチ」して2本指で画面を拡大したことあるよね?

その調子で、△ABCも拡大してみると、
ほれ!
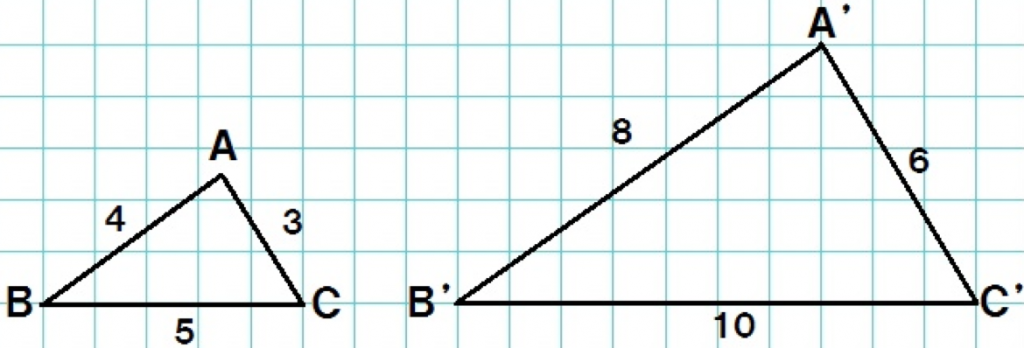
△ABCの2倍の△A’B’C’のできあがりさ。
この2つの三角形をつかって、
相似な図形の性質を確認していこうか。
相似な図形の性質の1つめは、
対応する線分の長さの比が等しい
ってやつだ。
つまり、ぜんぶの辺の比が同じになってるって性質ね。
それじゃあ、
「△ABC」と「2倍に拡大した△A’B’C’」の、
対応する辺を確認していこう。
対応する辺はそれぞれ、
だね。
色でわけてみたよ↓↓
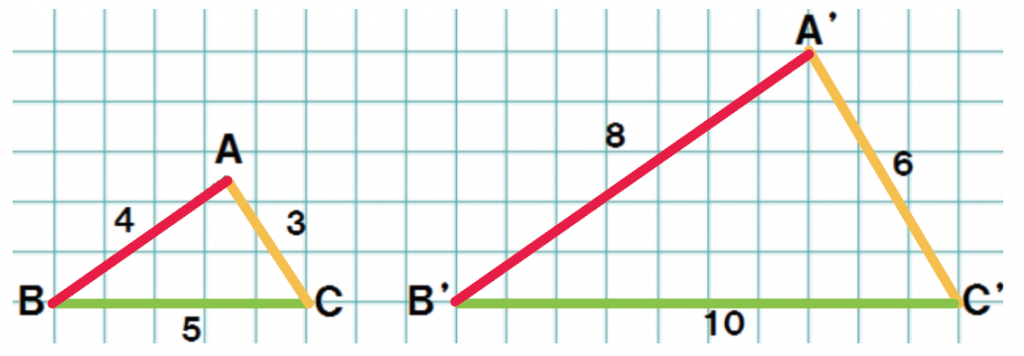
対応する辺の長さについて調べみると、
うんうん、
△A’B’C’ の辺の長さは△ABCの辺の2倍になってるね。
辺の長さの比を書くと、
になってるね。
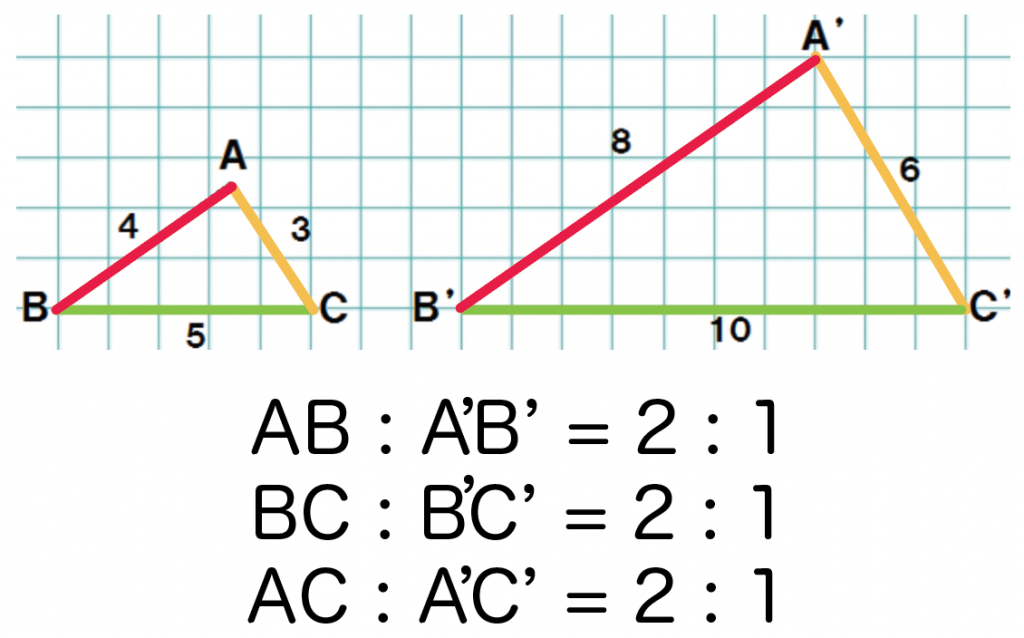
あ!
ぜーんぶの比が2: 1になっとるやん!
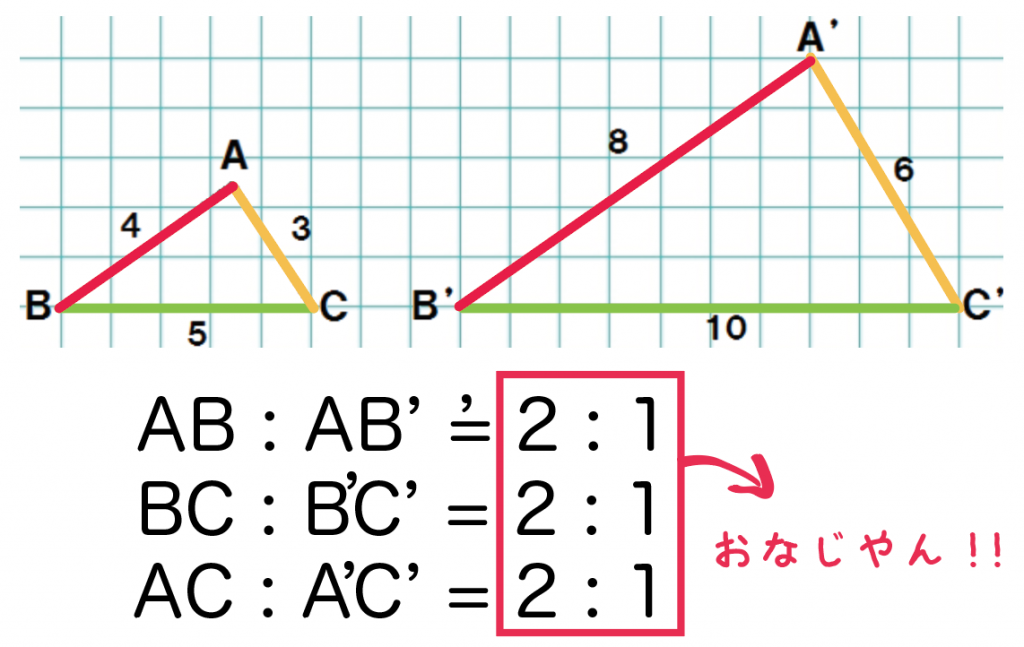
ってことは、
対応する辺(線分)の長さの比はすべて等しい
っていえるね。
これが相似な図形の1つめの性質だ。
2つめの相似な図形の性質は、
対応する角の大きさが等しい
ってやつね。
簡単にいってやると、
相似な図形の角度はぜんぶ等しいよ!
ってこと。
ためしに、△ABCと△A’B’C’をみてみようか。
実際に分度器で角度をはかってみると、
うわ!
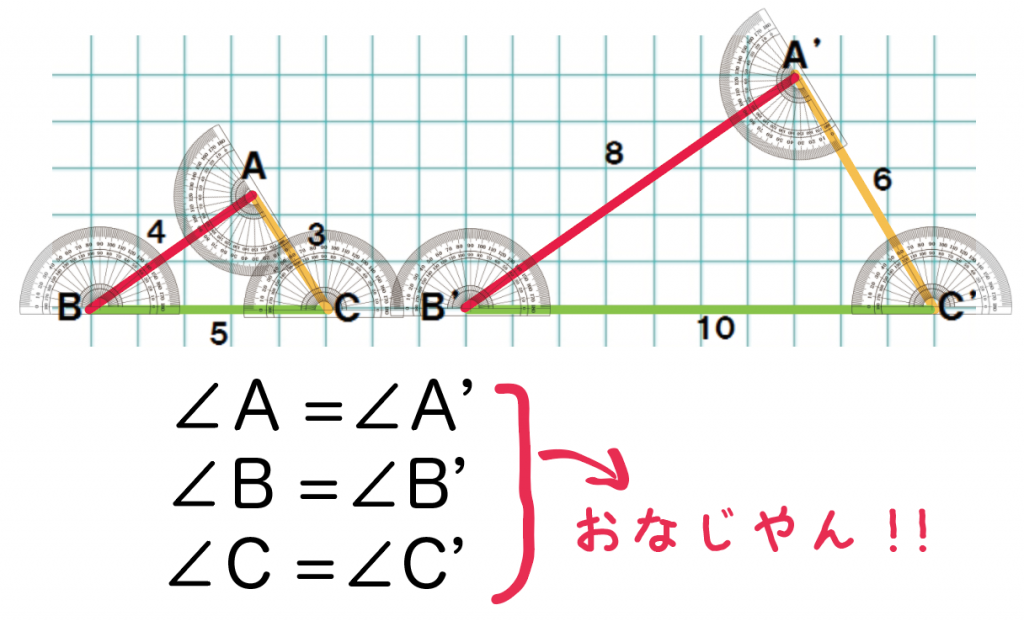
いっしょじゃん!
対応する角たちが等しくなってる!!
えっ。うさんくさいって??
そういうときは、2つの図形をかさねてみて。
ほら?
きれいに重なるでしょ?
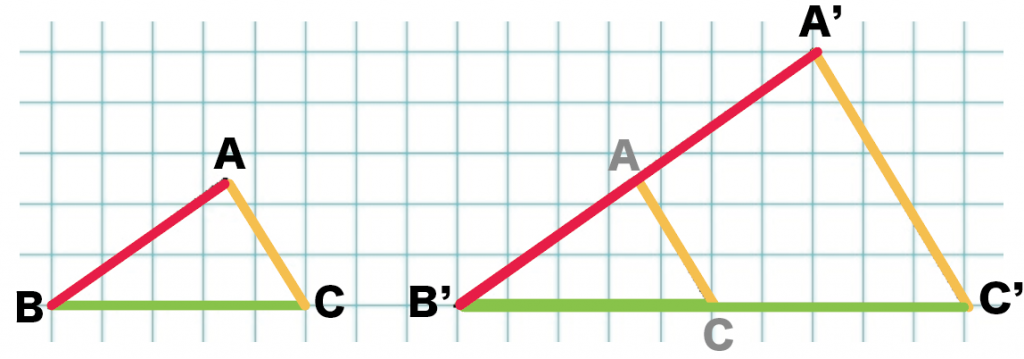
こんなかんじで、
2つの相似な図形の角度は、
ぜーんぶ等しいっていう性質があるんだ!
相似な図形の性質を忘れないように復習しておこう。
相似な図形の性質は、
の2つだったね??

この2つの性質は基本中の基本。
相似な図形を見たときに,
「あ,こことここの角度同じ!」
「相似だから,こことここの比が同じ!」
って気がつくことが大事。
相似の基本的なことだけど、重要だよ。
性質を必ず頭に叩き込んでおこう。
それじゃあ、
Drリード
どーも、ぺーたーだよ。
図形と相似の単元で、
中点連結定理
を勉強していくよね。
えっ、忘れたって!?
中点連結定理を簡単にいってやると、
三角形の2辺の中点を通る線が、
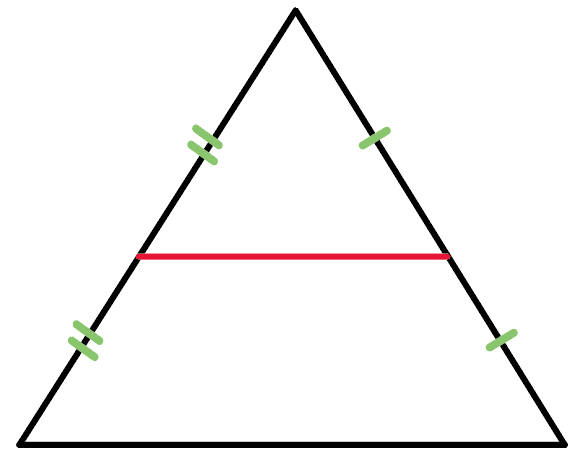
底辺に平行で、
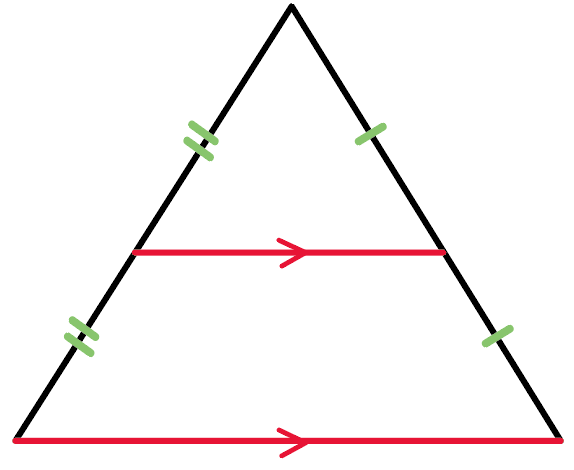
なおかつ、
底辺の半分になってるよー
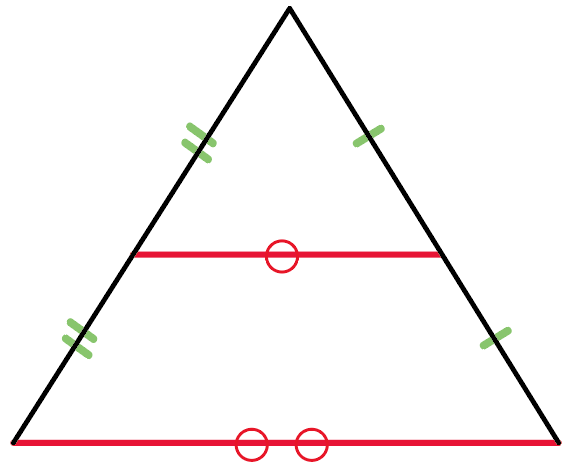
っていう定理なんだ。
けっこう便利なんだけど、
なんでそうなるの?
って思ったことはないかな?
思ったことがなくても、
中点連結定理を使えれば大丈夫なんだけどねw
ってことで、今日は、
なんで中点連結定理が使えるか??
を証明していくよ!
さっそく中点連結定理を証明していくよ。
3ステップで証明できちゃうんだ。
中点連結定理を証明するために、
つぎの、
△ADEと△ABC
を思い浮かべてみて。
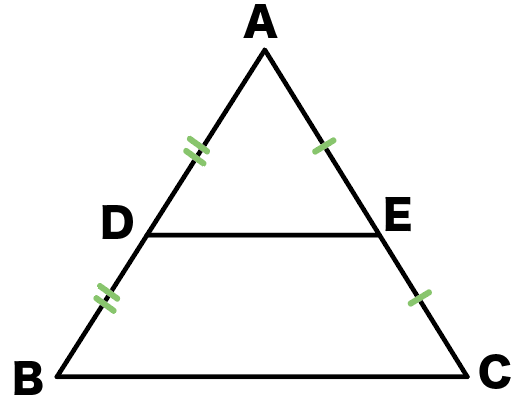
DとEはそれぞれ、ABとACの中点ね。
中点連結定理の証明のゴールは、
を証明することだよ。
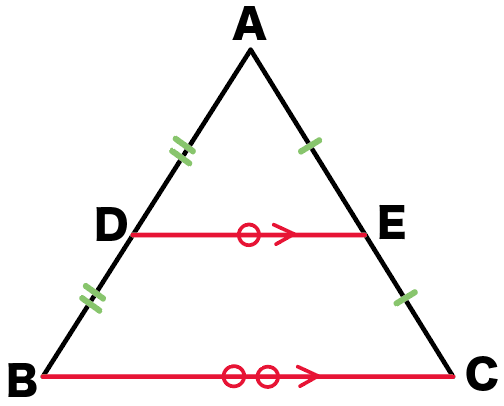
さっそく証明していこう!
まずは△ADEと△ABCの相似の証明だ。
D・Eはそれぞれの中点だから、
だよね??

ってことは、比であらわすと、
になるはずなんだ。
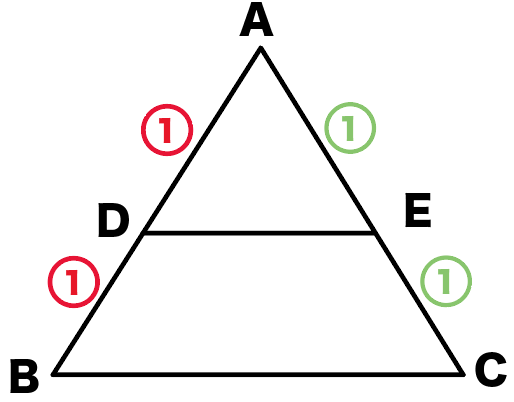
ADとDBの比を合わせると、
AD:AB=1:2…①
ACの比も同じ考え方でAEとECの比を合わせると、
AE:AC=1:2…②
になるね。
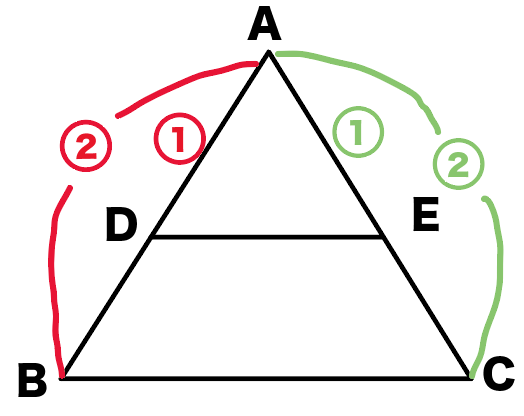
んで、
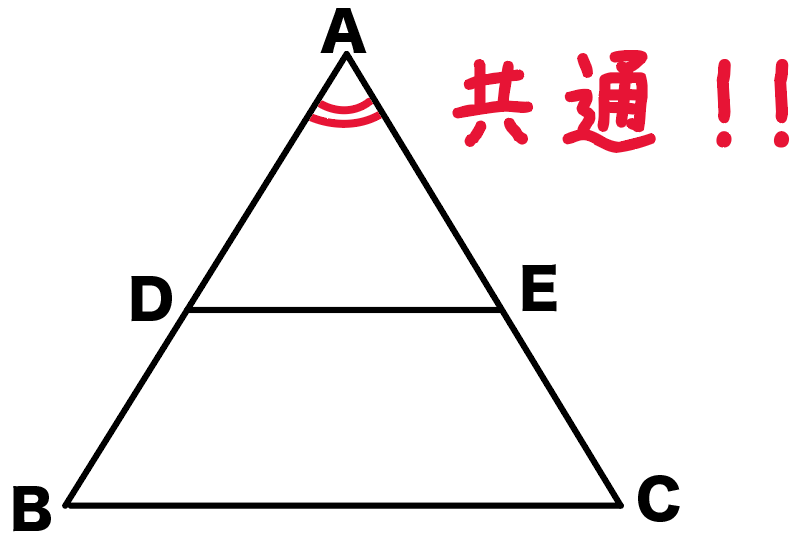
△ADEと△ABCは角Aを共有してるよね??
ってことで、
角DAE = 角BAC (共通)…③
だ。
①、②、③より、三角形の相似条件の、
2組の辺の比とその間の角がそれぞれ等しいが使えるから、
△ADE∽△ABC
になるね。
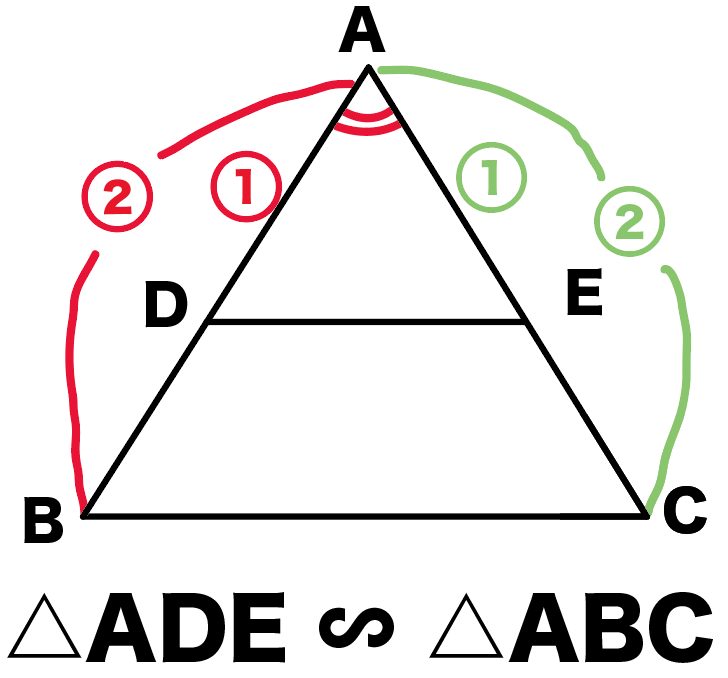
これで相似の証明はできた!
三角形の相似比を求めてみよう。
①のAD:AB=1:2より、
△ADEと△ABCの相似比は1:2になるよ。
なぜなら、
ADとABは対応してる辺どうしだからね。

つまり、
△ADEと△ABCの対応する辺の比は全て、
1:2になるはずなんだ。
ってことは、残りの対応する辺の、
DEとBCの相似比も1:2になるね。
DE:BC=1:2
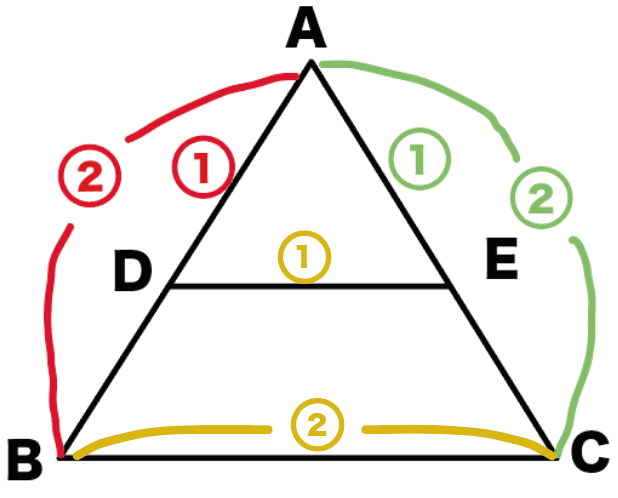
こいつを別の言い方をすると、
DE=1/2BC
ともできるよね。
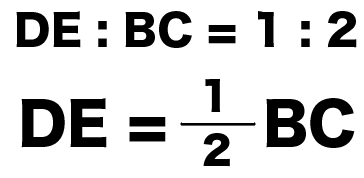
これでDEがBCの半分になるってことはわかったね!
あとは、
DEとBCが平行であること
を証明していこう。
これで中点連結定理の証明が完了するね。
平行の証明には、
同位角が等しいこと
をつかっていくよ。
△ADE∽△ABCだから、相似の図形の性質をつかうと、
対応する角はすべて等しいはずだね。
ってことは、
角ADE = 角ABC
がいえちゃうんだ。
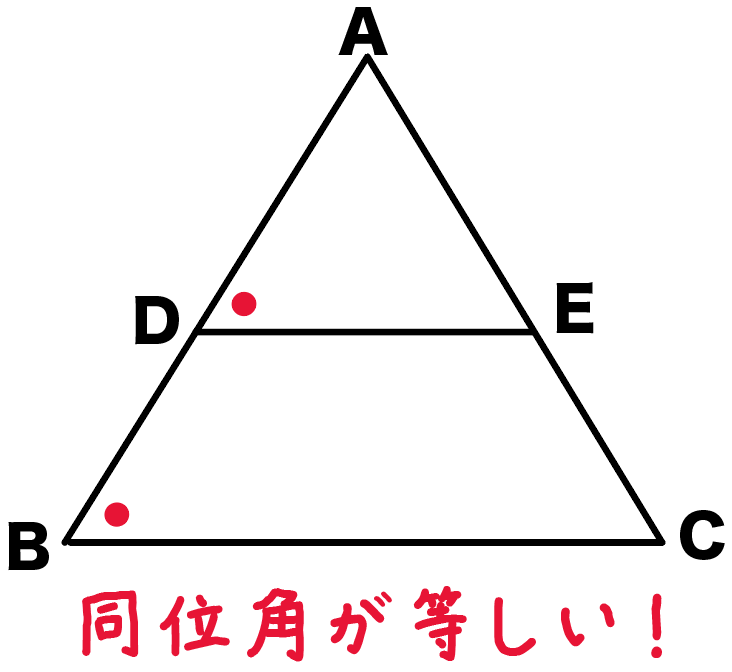
こいつらは、どうみても同位角。
同位角が等しいから、
同位角をつくってるDEとBCは平行
ってことがいえるんだ。
ってことで、
DE // BC
になるよ。
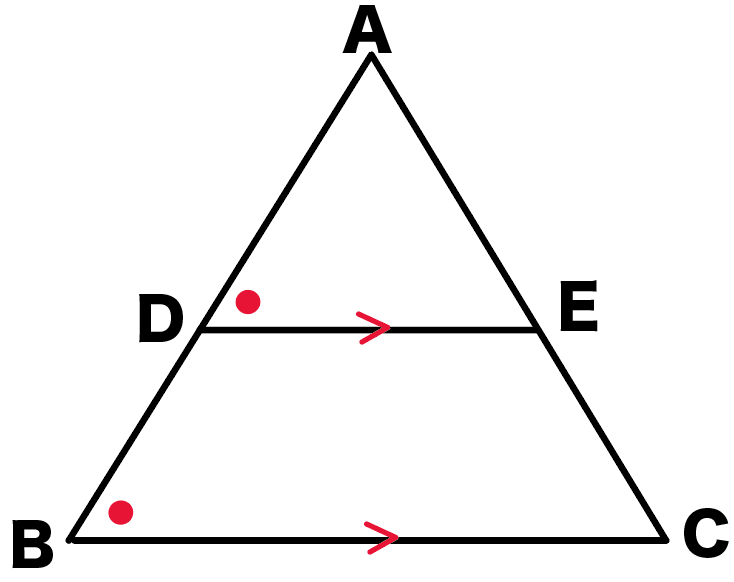
ここまでの3つのステップから、
DE//BC
DE=1/2BC
であることが言えるんだ。

おめでとう!
中点連結定理を証明できたね!!
ここまでで、中点連結定理は証明できたね??
べつに証明はできなくてもいいけど、
なぜ、中点連結定理がつかえるのか??
ということは、ふんわりでもいいから頭の片隅においておいてね。
じゃ、またね!
ぺーたー
こんにちは!ぺーたーだよ。
相似の単元の勉強はどうかな??
相似の証明問題だったり、
相似比を求める問題が出たり
あれこれ大変だね。
今日はもう1つ新しい、
相似比をつかった体積の比の求め方
を解説するよ!
ついでに表面積の比の出し方も説明するから、
セットで覚えてあげよう。
相似比から体積比をだすときは、
つぎの公式をつかってみよう。
それは、
相似比の3乗が体積比になるよ
っていう公式だ。
くわしくいうと、
2つの相似な立体があって、相似比がn:mのとき、
2つの立体の体積比は、
n^3 : m^3
になるってこと。
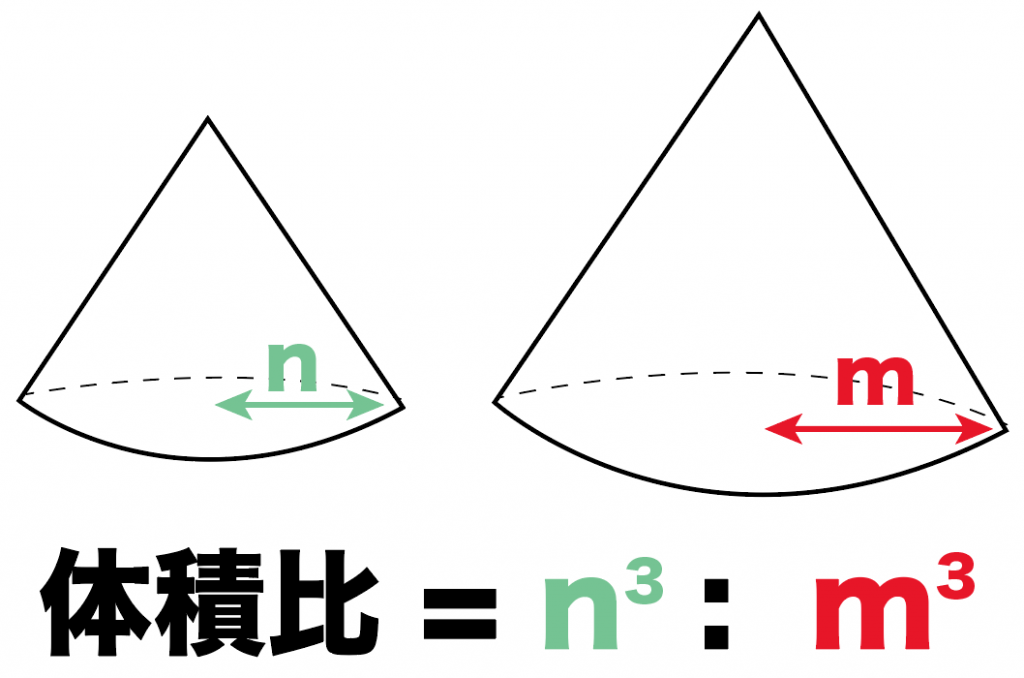
この公式で練習問題をといてみよう。
練習問題
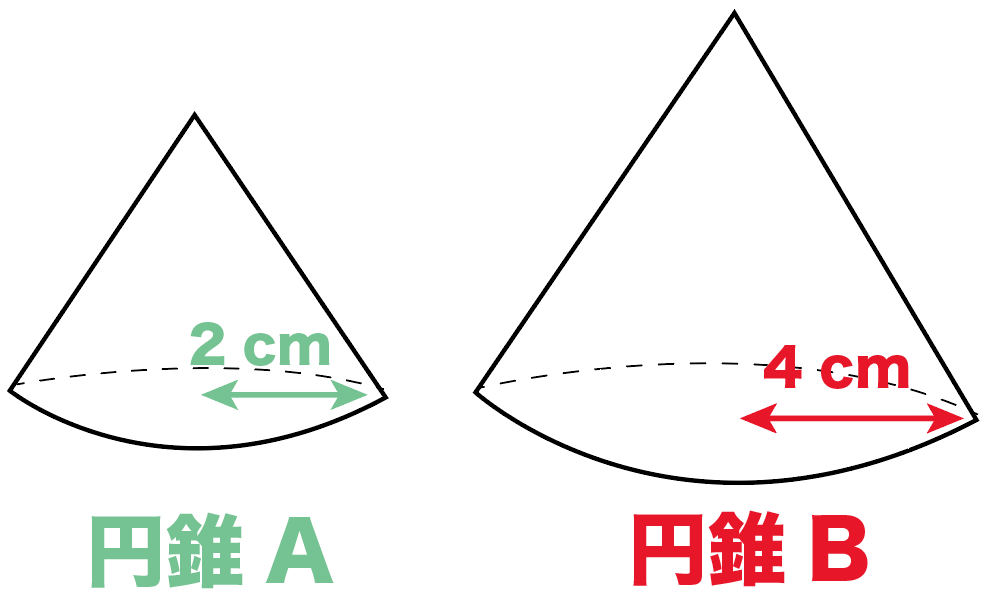
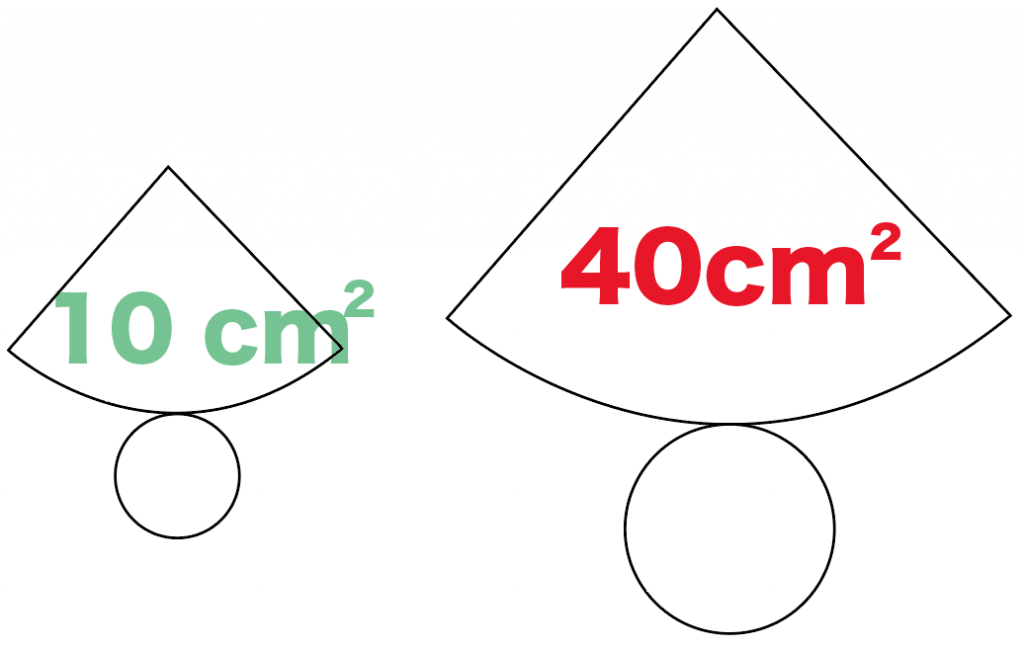
次の円錐は相似の関係です。
体積比と表面積の比を求めてください。
この体積比の問題は、2ステップでとけちゃうんだ。
立体の体積比を求めるには、
相似比
が必要なんだ。
練習問題をみてみると、
2つの円錐は相似である
ってかいてあるね。
わざわざ相似を証明する必要ないからうれしい!
さっそく相似比を求めてみよう。
対応する辺を「半径」として、相似比をもとめてみてね。
2つの円錐の底面の半径はそれぞれ、
だったよね??
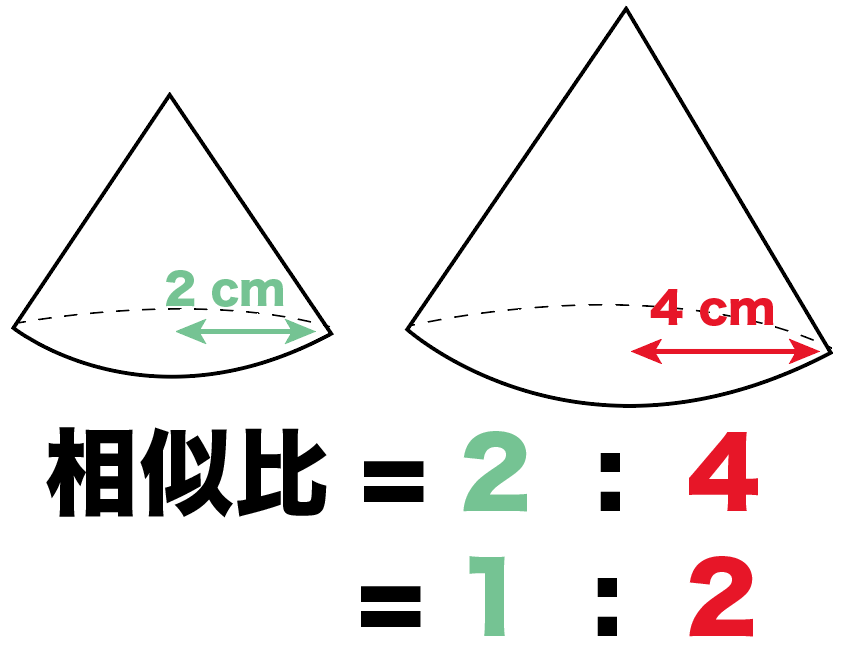
ってことは、こいつらの相似比は、
2: 4
= 1: 2
になるんだ。
相似比が出たら、
体積比はとっても簡単!
体積比の公式の、
相似比を3乗してやると体積の比になる
を使えばいいのさ。

練習問題でも体積比の公式をつかっていこう。
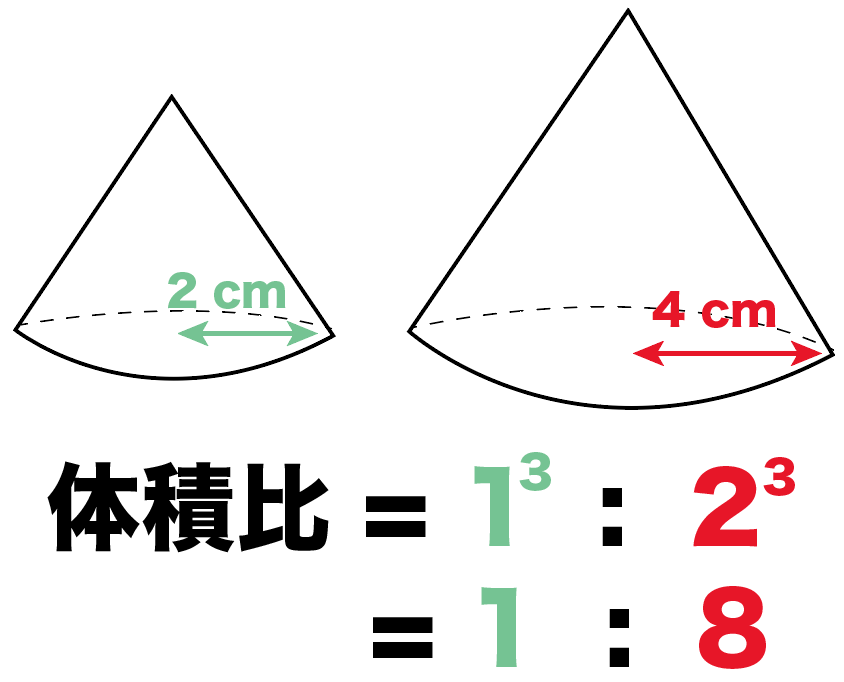
相似比は1:2っていうことがわかったね。
体積比はその相似比を3乗した、
1^3:2^3
= 1 : 8
になるね。
ってことで、
この2つの立体の体積比は「1 : 8」。
やったね!
えっ。
体積比は何の役にたつのかって??
じつは、体積比がわかると、
「ある立体の体積」から「べつの立体の体積」が計算できちゃうんだ。
たとえば、さっきの練習問題で、
円錐Bの体積が80 [cm^3]だったとしよう。
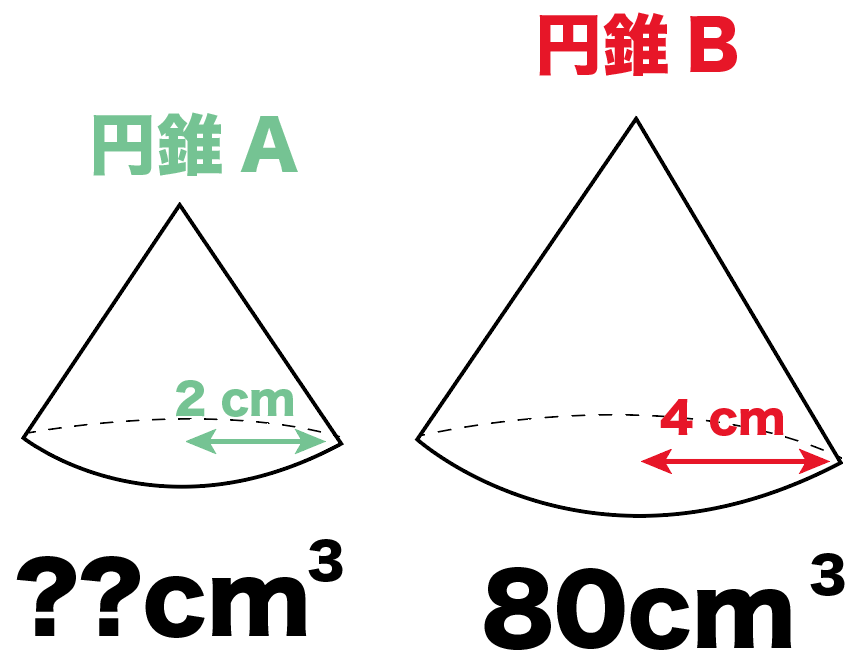
この2つの立体の体積比は、
1: 8だったよね??
ってことは、
「円錐Aの体積」は「円錐Bの体積」の8分の1。
ってことは、円錐Aの体積は、
(円錐Bの体積)×1/8
= 10 [ cm^3 ]
になるんだ。
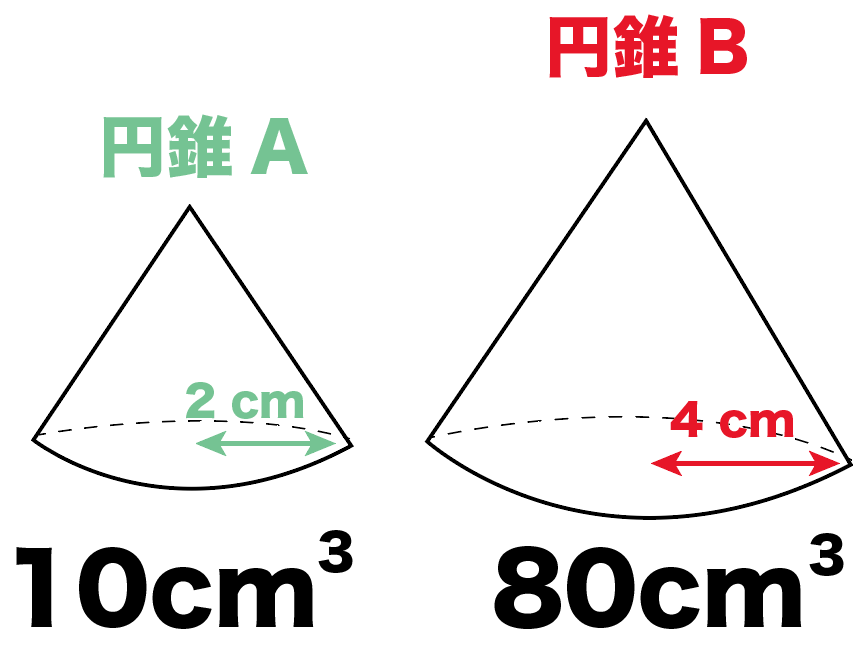
ね??
体積比をつかうと立体の体積がわかっちゃうんだ!
相似比から体積比が求められたね!
おめでとう・・・・・・!!
っていうのはまだはやい。
じつは、練習問題の最後に、
表面積の比も求めなさい
ってかいてあるじゃん?
せっかくだから、表面積の比も相似比から計算してみよう。
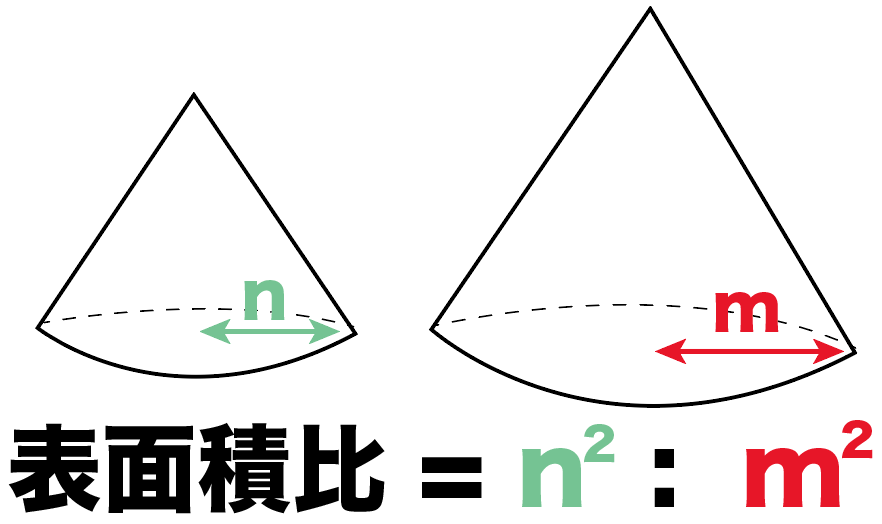
ずばり、表面積の比の求め方は、
面積比の求め方といっしょ。
つまり、
相似比の2乗の比になってるのよ。
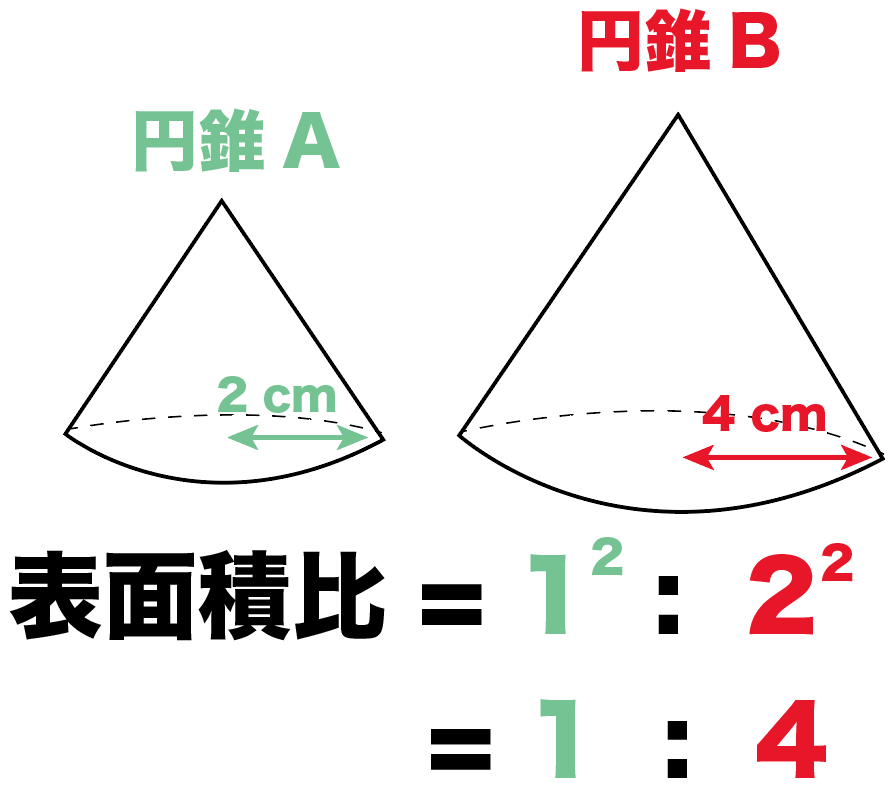
相似比が1:2の「円錐A・Bの表面積の比」は、
1^2 : 2^2
= 1 : 4
になるわけね。
もし、円錐Bの表面積が40 [cm^2]だったら、
円錐Aの表面積は10 [cm^2]
になるわけだね。
おめでとう!
相似比から表面積の比も求められたね!
体積の比も、表面積の比も公式を覚えちゃえば楽勝。
しっかり公式を覚えてあげようね。
問題をときまくって段々なれていこう!
じゃあ、またね
ぺーたー
どーも、ぺーたーだよ。
中点連結定理をつかった証明問題はたくさん、ある。
なかでもよくでてくるのは、
平行四辺形であることを証明する問題
だ。
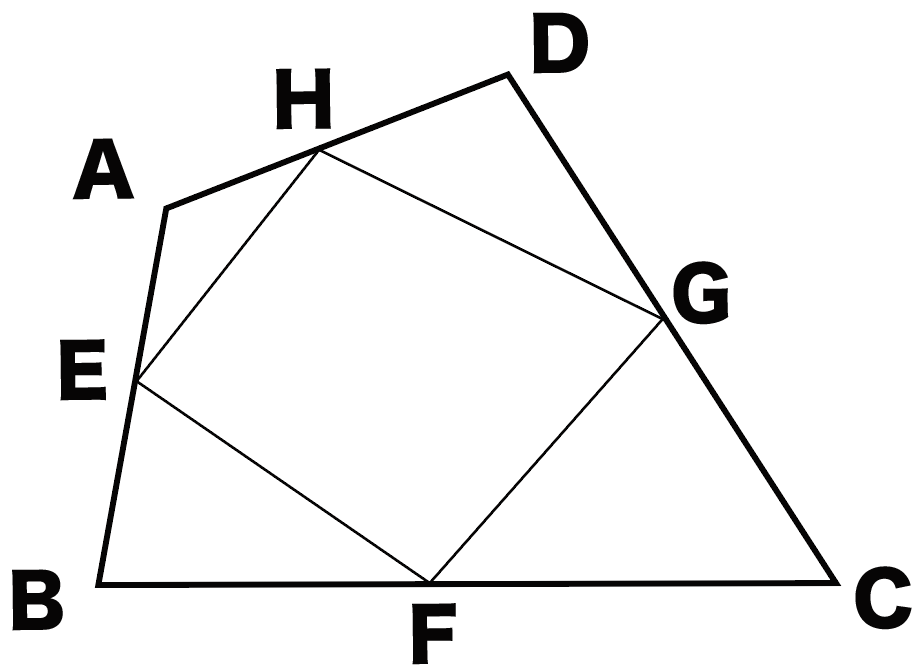
たとえば、つぎみたいな証明問題ね。
このとき四角形EFGHが平行四辺形になることを証明しなさい。
みんなけっこう難しいって
思ってるんじゃないかな?
今回はどうやって、
中点連結定理で平行四辺形を証明するのか
を3ステップで証明していくよ。
さっそく証明問題をといていくよ。
四角形ABCDの4辺AB、BC、CD、DAのそれぞれの中点をE、F、G、Hとする。
このとき四角形EFGHが平行四辺形になることを証明しなさい。

証明を始める前に1つだけやることがあるんだ。
それは、
対角線を1本かいてあげること!
そうするとこうなるね ↓↓
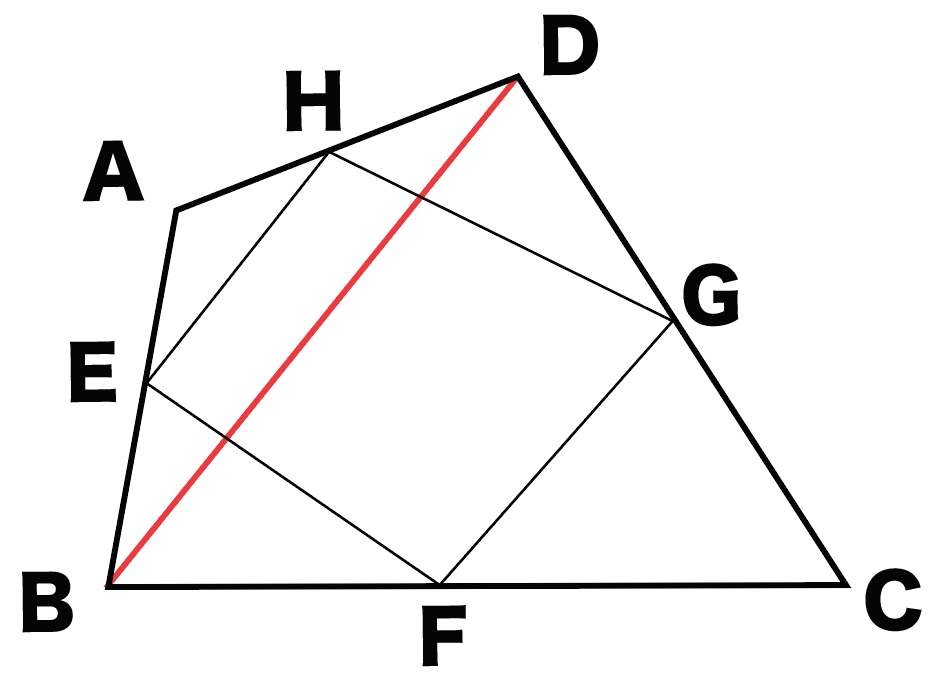
今回は、対角線BDをひいたけど、ACでも同じだからね。
対角線を引いたら、いくつか三角形が見えてくるよね?
練習問題でいうと、
の4つだね。

平行四辺形を証明するために
2組の三角形に分けてみてみよう。
まずは△AEHと△ABDに注目してみて。
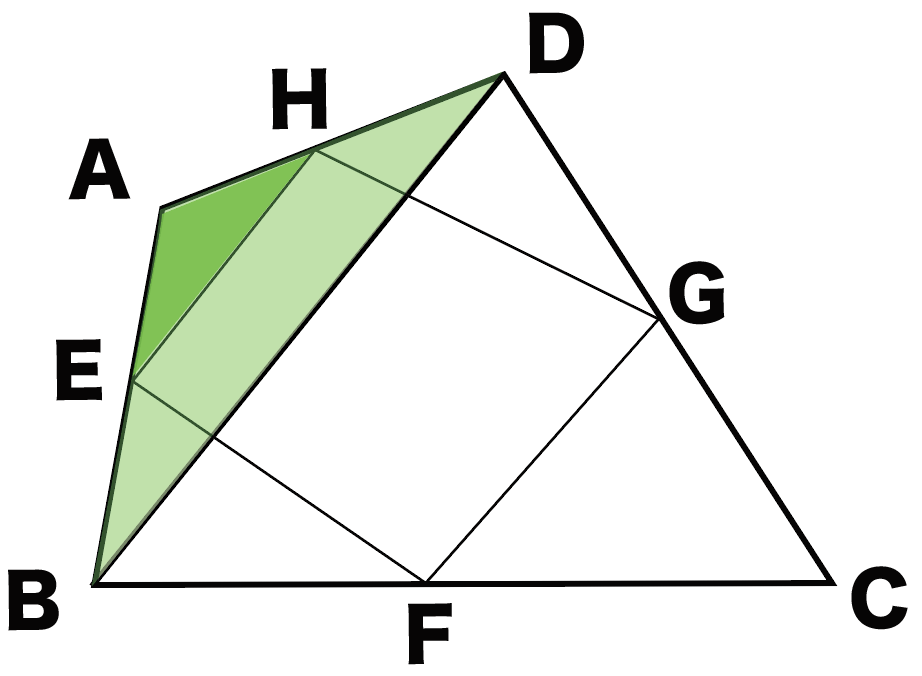
EとHはそれぞれ、
辺ABと辺ADの中点だよね??
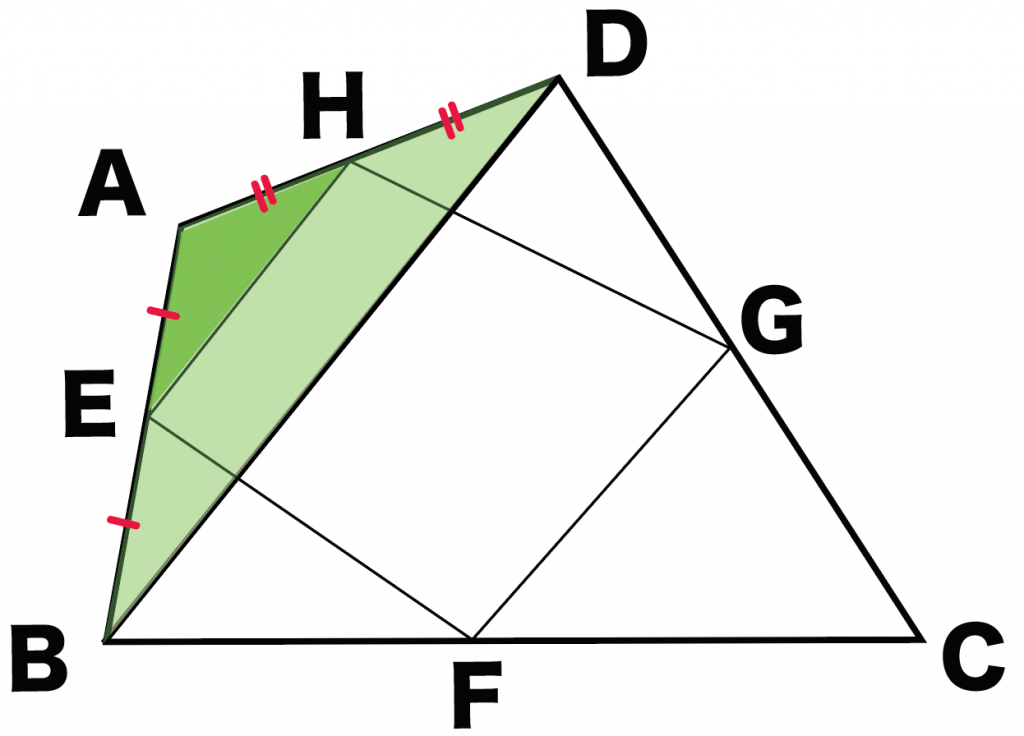
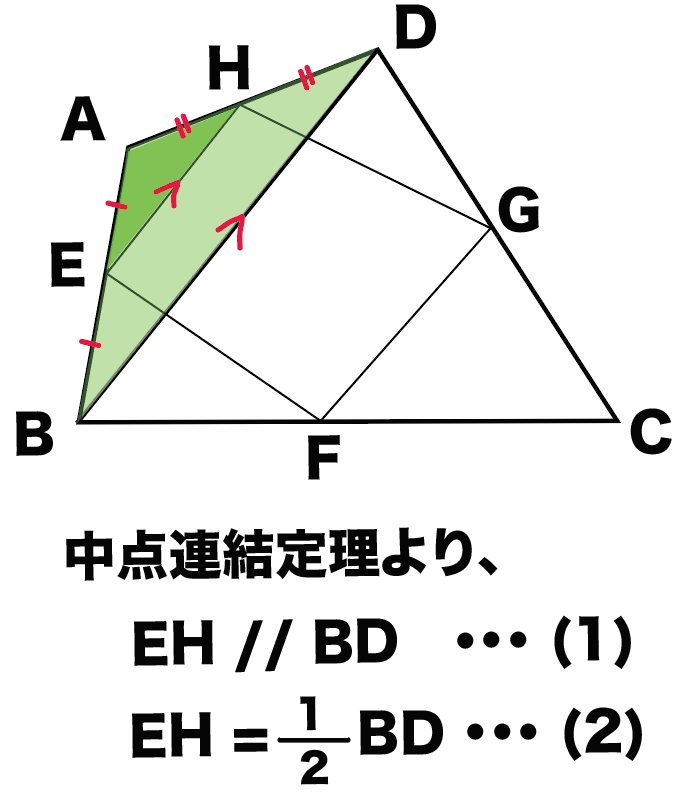
ってことは、中点連結定理をつかうと、
EH // BD・・・(1)
EH = 1/2 BD・・・(2)
がいえるんだ。
おなじことを△CGFと△CDBでもやってみよう。
FとGは、辺BGと辺DCの中点。
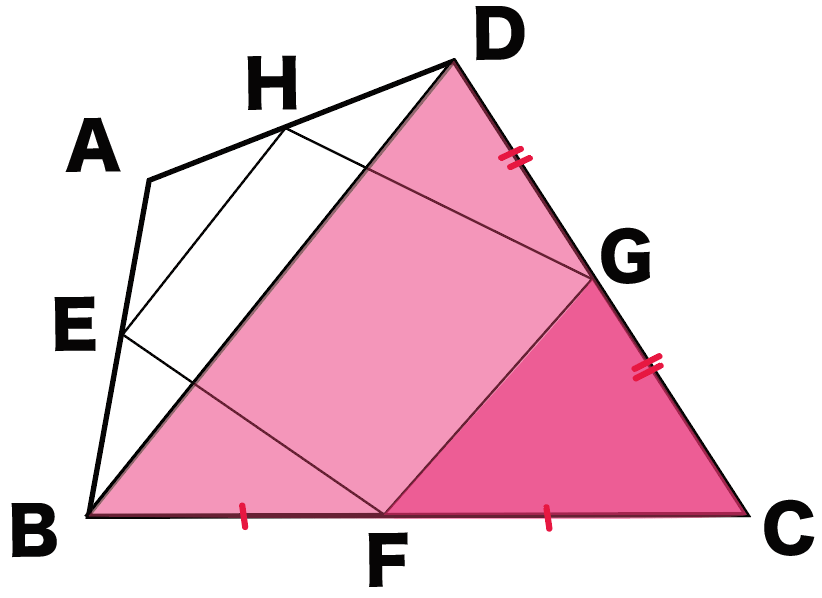
ってことで、中点連結定理がつかえるから、
FG // BD・・・(3)
FG = 1/2 BD・・・(4)
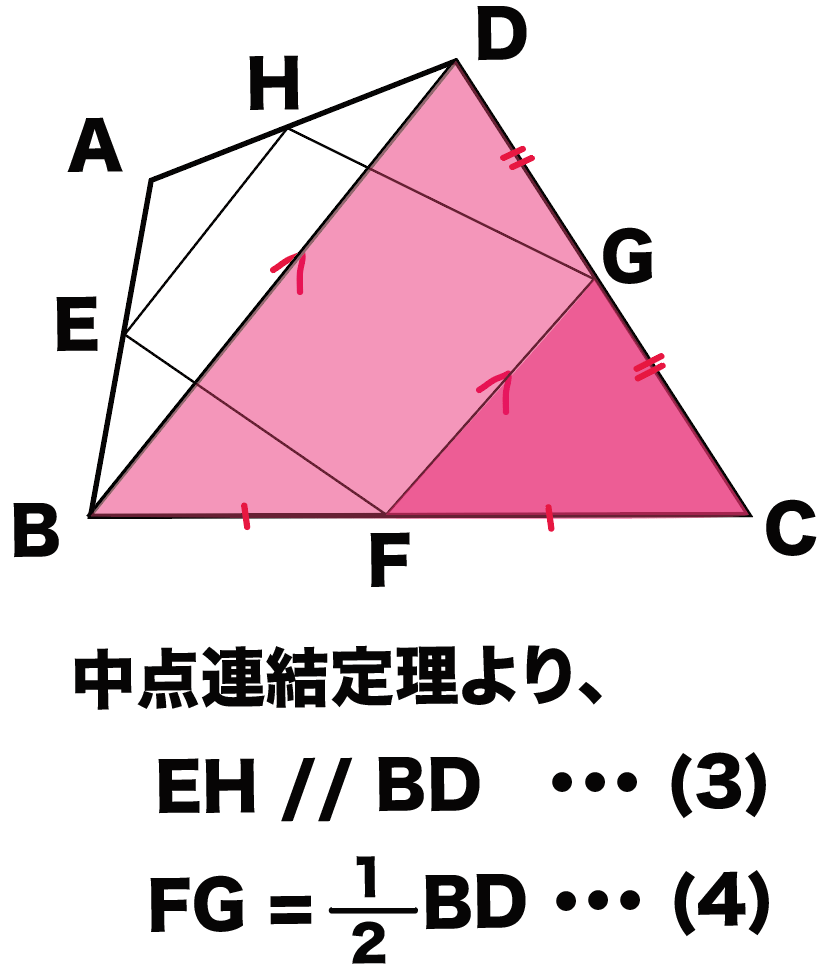
になるね。
最後は平行四辺形になる条件をつかうよ。
5つの条件を見なくても言えるかな?(。)
くわしくは平行四辺形になるための5つの条件をよんでみてね。
ちなみに、中点連結定理を使って平行四辺形を証明する問題は
1組の対辺が平行で長さが等しい
を使うのがほとんど。
今回もこの条件をつかうよ。
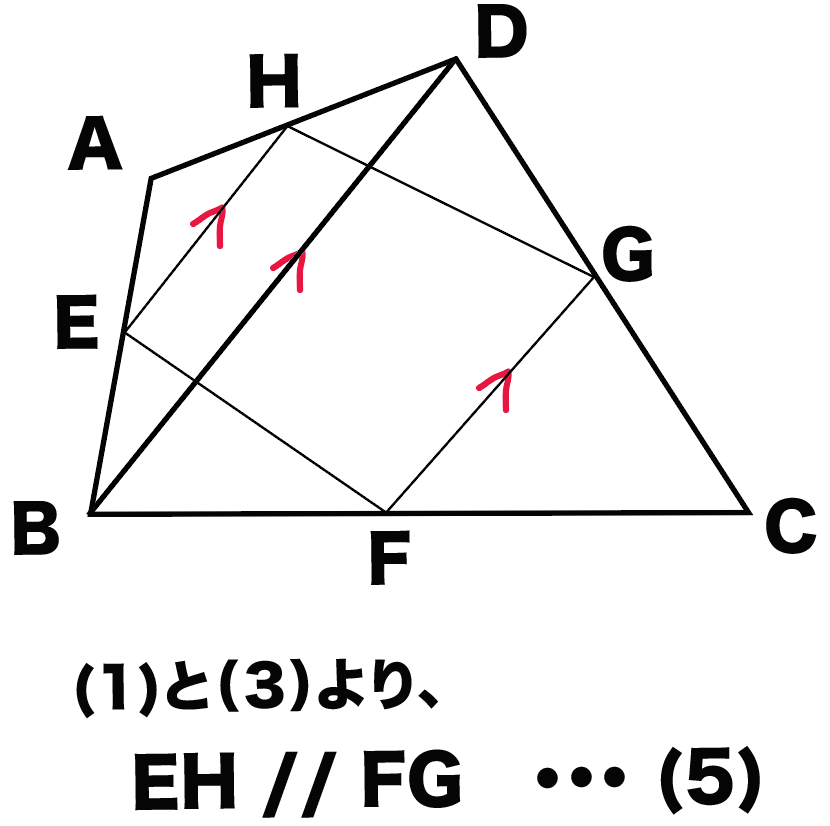
(1)と(3)から、
EH//BD//FGになるね。
つまり、
EH//FG・・・(5)
がいえるわけだね。
また、(2) と (4)から、
EH = FG = 1/2 BD・・・(6)
がいえるね。
EHとFGの両方がBDの半分になってるからさ。
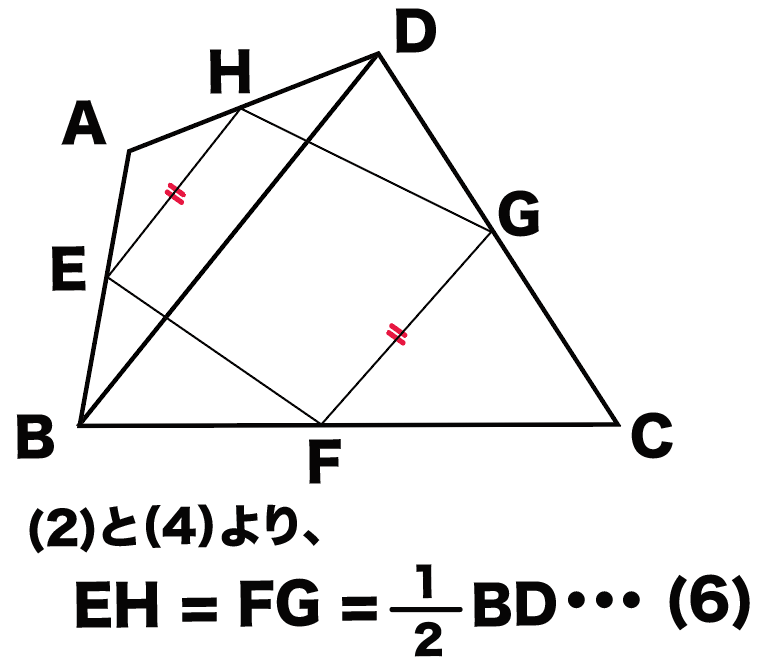
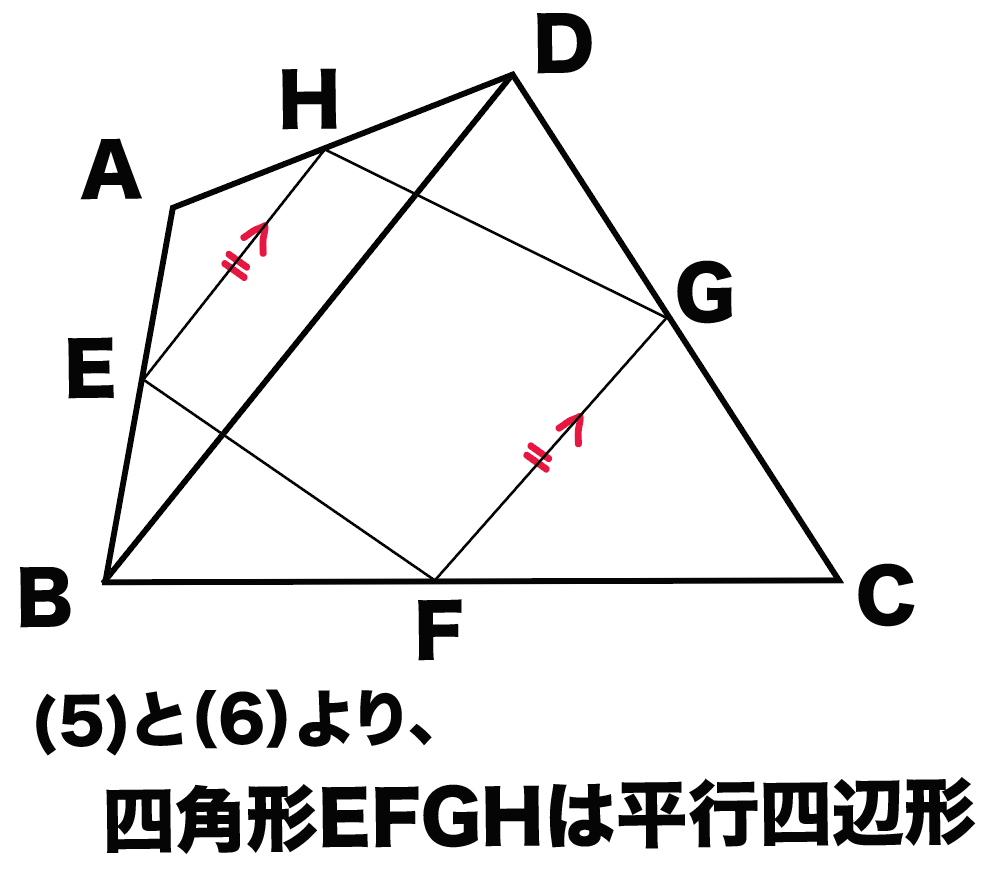
んで、
(5)と(6)より、平行四辺形になる条件の、
1組の対辺が平行で長さが等しい
がつかえるわけだね。
だから、
四角形ABCDは平行四辺形
ってわけ。
おめでとう!
これで証明おしまい!
中点連結定理をつかった平行四辺形の証明はどうだった??
この問題のポイントは、
対角線の補助線がひけるかどうか
だね。
平行四辺形を証明する問題は数をこなすのが一番!
おぼえるまで何回かといてみてね。
じゃあねー
ぺーたー
ある日、数学が苦手なかなちゃんは、
相似と合同の違いがわからなくなってしまいました。

どっちも図形の問題だね。
いっとくけど、
相似と合同はべつものだよ。
えー!
でも、2つの図形を比べるとか、
ちょっと似てない?
どっちかわかんなくなる。
確かに、ちょっと紛らわしいかも。
違いを見つけていこう!
ういす!!
相似と合同の違いはつぎの3つかな。
3つもあるんだ!
たいへん!!
ゆっくりみていけば大丈夫。
それじゃあいくよー!
まずは言葉の意味から!
えっと・・・・
合同が「同じ」で、
相似が「似る」・・・・・?

うわ! ぴったり重なった!!
すげえ!
じゃあ相似は??
こんな感じで、形は一緒だけど、
大きさが違う!

なんか、拡大コピー見てるみたい。
そうだね!
小6で出てきた『拡大と縮小』を思い出せるといいね。
あー!あいつか!
対応している角度
と
辺の比
が等しくなっているんだ。
へー!
くわしくは、
相似な図形の性質を復習してみてね。
相似と合同では、
成立条件
に違いがあるよ。
せいりつじょうけん??
へー!
合同条件と相似条件ってことかな??
そうそう!
三角形の相似条件と合同条件をみてみよっか!

パッと見ただけじゃわからない…
じゃあ、
1つ目の条件を見比べてみよう!
1つ目?あっ!
相似は辺の「比」が等しいけど、
合同は辺の「長さ」が等しいとこかな!
そう!
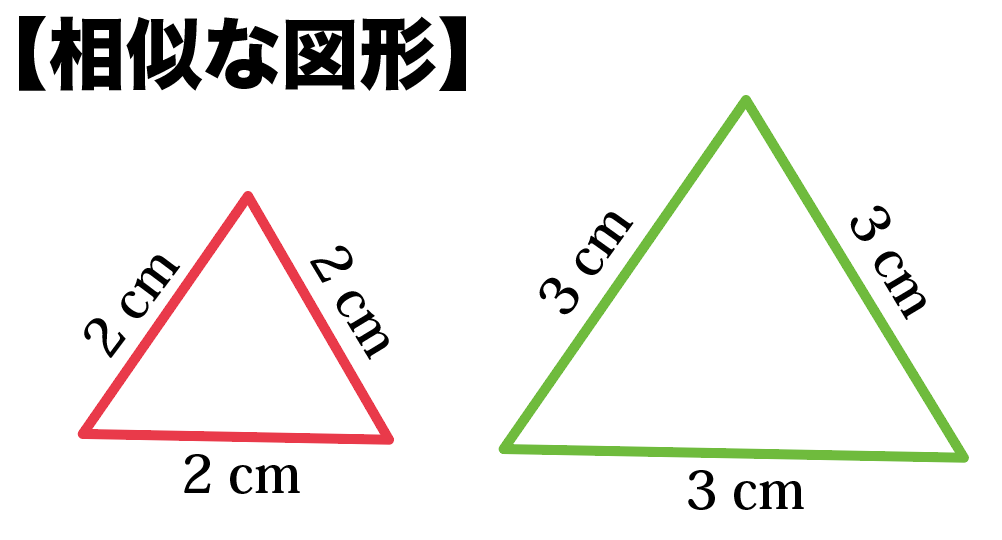
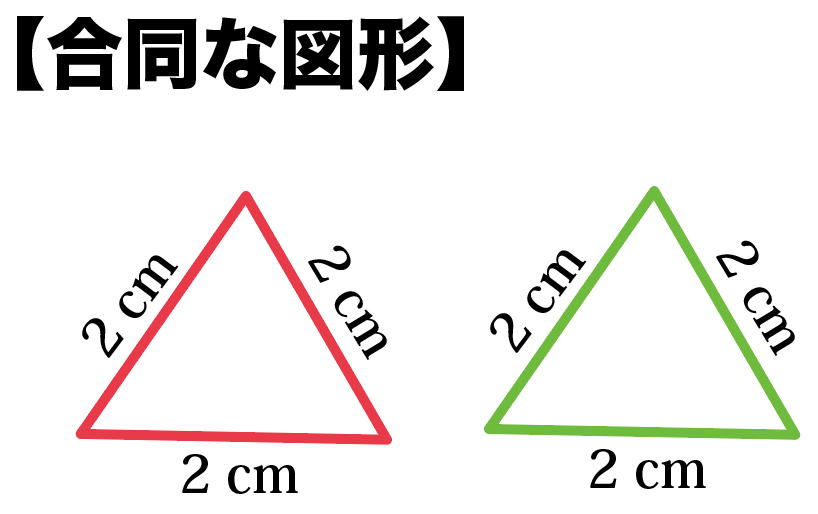
図で表すとこんな感じ。
下の三角形は辺の比が1: 1: 1だから、
辺の比が等しい。
だから、相似っていえる!
なるほど!
一方、
辺の長さがぜーんぶ等しかったら、
合同っていえるわけ。
なるへ!
くわしくは、
「三角形の合同条件と相似条件の違い」
をよんでね。
記号の違いもある!
今回紹介する最後の違いだ!!
うす!!
相似と合同の記号のはつぎのやつだよ↓↓

めっちゃ違うじゃん!!
そうだね。
相似記号は、
アルファベットのSを横に倒したような記号。
合同記号は、
=に一本書き足したような記号
になっているね。
書き間違えないようにしようっと!
どう??
相似と合同の違いはわかったかな??
えっと、
『合同』は全く同じ図形だから、辺の長さまで同じ。記号は『≡』。
『相似』は似ている図形だから、辺の長さの比が一緒になる。記号は『∽』。
完ぺきじゃん!
『似ているけど同じじゃない』
それが『相似』だ!
やったあーー!
やあ、ぺーたーだよ。
中3になると、相似を勉強するよね。
覚えること多くて大変。
相似の証明したり、相似比を求めたり…ほんといろいろ。
中でもよくでてくるのが、
相似比から面積比を求める問題。
むずかしそうにみえるけど、公式さえ分かってれば大丈夫。
面積比は絶対に求められる!
今日はこの面積比の公式を紹介していくよ〜
面積比にはつぎの公式があるよ。
「面積比」は「相似比の2乗」になる
ってやつだ。
たとえば、△ABCと△A’B’C’の相似比が「n:m」だとしよう。
このとき面積比は、
n² : m²
になってるんだ。
せっかくだから、この面積比の公式をつかってみよう。
つぎの2つの三角形をイメージしてみて。
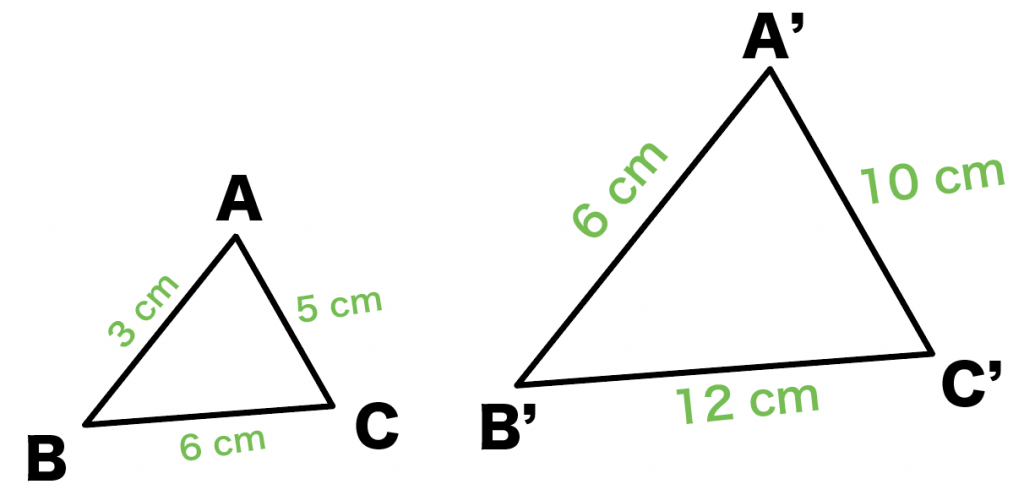
△ABCと△A’B’C’の辺の長さがそれぞれ、
と、
になってるよ。
この2つの三角形の面積比をだしてみよう!
公式なら2ステップで面積比だせちゃうんだ。
まず相似比を出してやろう!
相似比の求め方は覚えてる??
相似な図形同士の、
対応する辺の長さの比
を求めればよかったね??
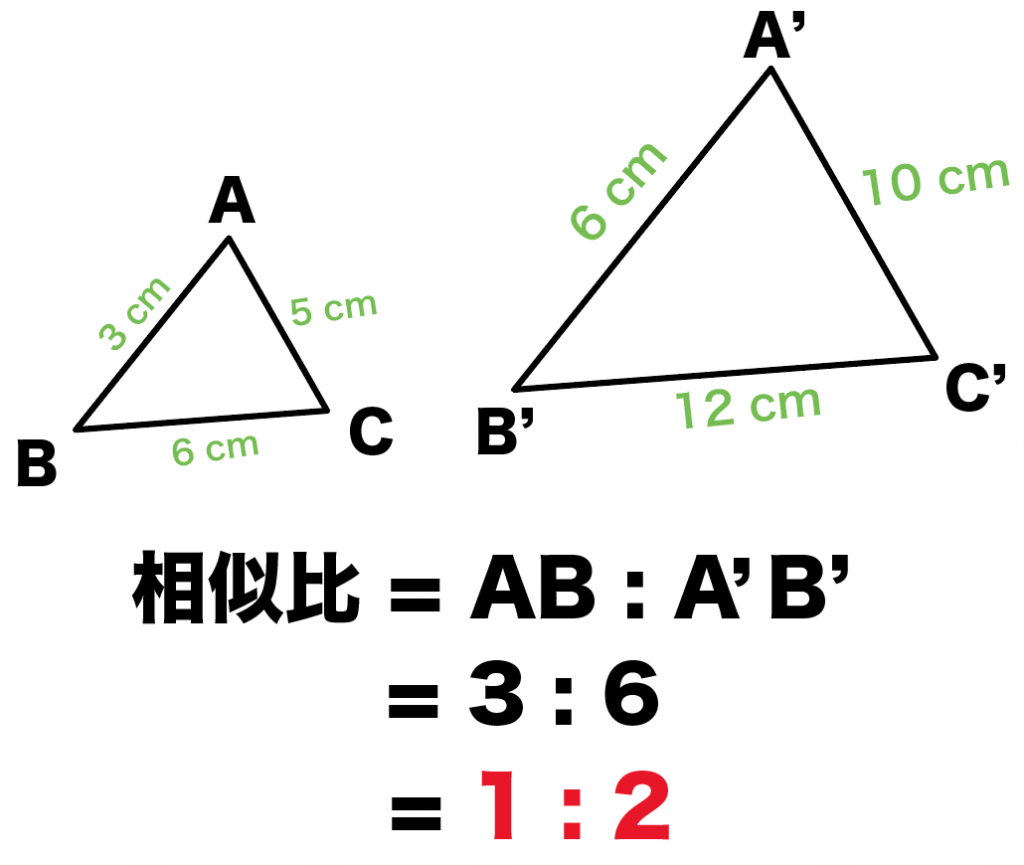
今回でいうと、辺ABに対応する辺は辺A’B’。
AB=3cm, A’B’=6cmだから、
相似比は、
AB : A’B’
= 3: 6
= 1 :2
になるね。
相似比が出ちゃえばあとは簡単。
相似比を2乗すれば面積比がでるってわけ。
△ABCと△A’B’C’の相似比は、
1: 2
だったね??
面積比は2乗してやった比の、
1² : 2²
= 1 : 4
になるはず!
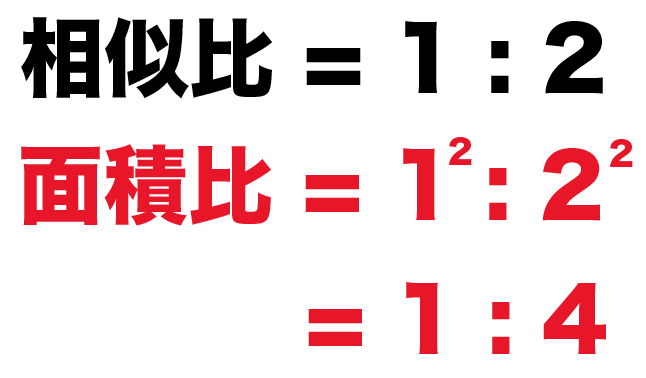
おめでとう!
相似比から面積比を計算できちゃったね。
面積比の公式でもう1つ問題を解いてみよう。
公式はつかっておぼえるのが一番!
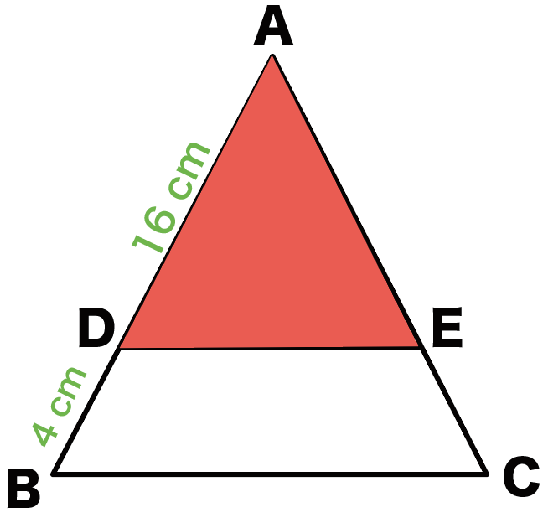
つぎの図の△ABCにおいて、AD = 16cm、DB = 4cmで、
△ADEと△ABCは相似です。
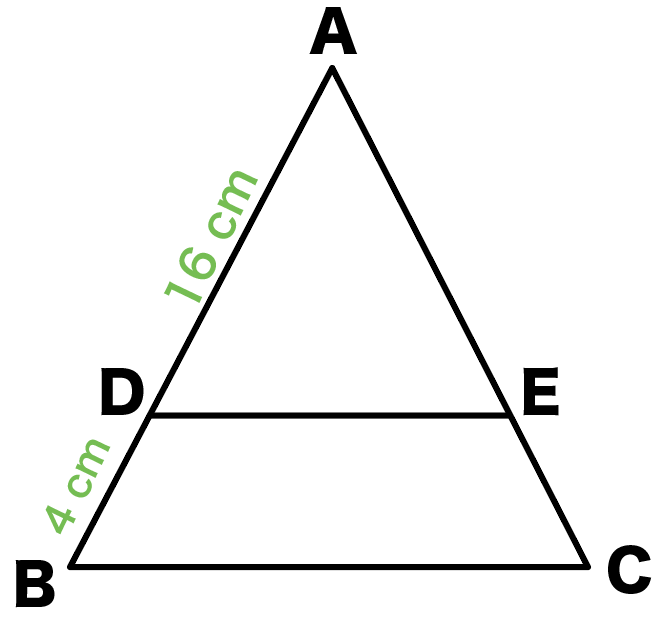
まずは相似比を求めるよ。
この場合、対応する辺は分かるかな?
色で分けるとこうなるよ!
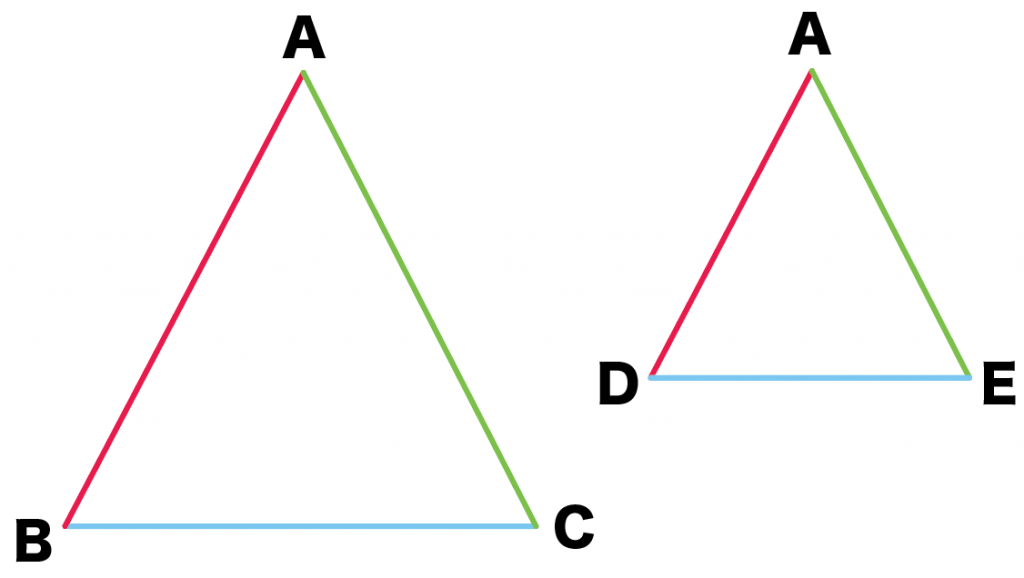
この問題では、ADの長さ(16 cm)が分かっているから、
赤色の辺を使って考えてみよう。
ABの長さはわかるかな?
そう、そうだね。
AB
= AD + DB
= 16 + 4 = 20
になってるはず。
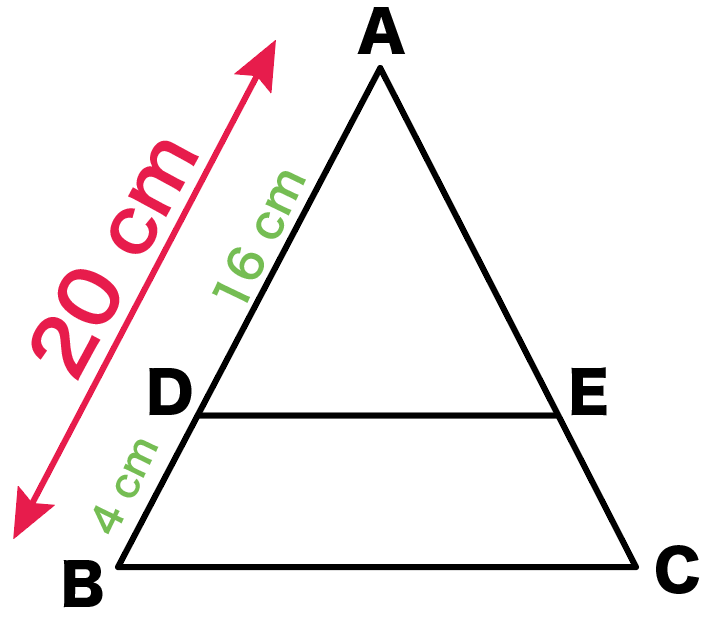
AD=16cm、AB=20cmだから、
相似比は…
△ADE : △ABC
= 16 : 20
= 4:5
だ!
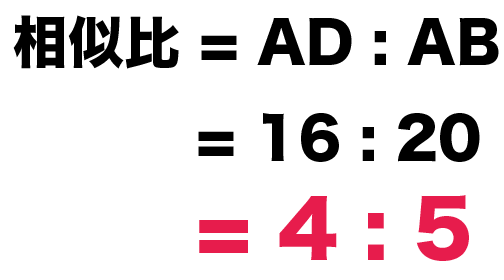
面積比はさっきの公式で一発!
面積比は相似比の2乗になる
だったよね??
この公式をあてはめると、
面積比
= 4² : 5²
= 16 : 25
になるね。

ってことで、答えは16:25!
最後は△ADEの面積だ。
さっきの面積比で求めていくよ。
△ADEの面積がわからないから、x[ cm²] とでもしておこう。
んで、
△ADEの面積:△ABCの面積 = 面積比
っていう比例式をつくってみようぜ。
だから、比例式は、
△ADEの面積:△ABCの面積 = 16 : 25
x : 50 = 16 : 25
になるね。
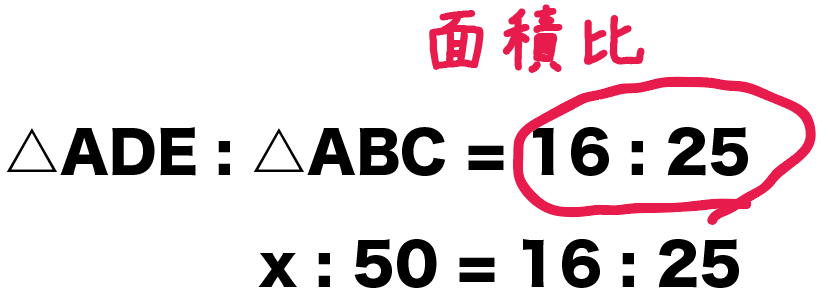
比例式の解き方でといてやると、
x : 50 = 16 : 25
25 x = 16×50
x = 32 [cm²]
になる。
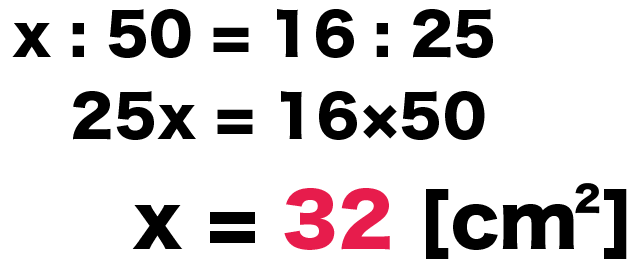
つまり、
△ADEの面積は32 [cm²]ってわけ!
相似比で面積比もとめられた??
相似比の2乗が面積比になる
っていう公式さえおぼえてれば怖くない。
面積比を求める問題はきっと大丈夫!
じゃ、またね!
ぺーたー
こんにちは!この記事をかいてるKenだよ。肉摂取しすぎたね。
図形と相似の単元では、
相似の利用
を勉強していくよ。
相似を日常でもつかってみよう!
っていう単元。
なかでもよくでてくるのが、
校舎の高さを求める問題
だ。
今日は、この問題のパターンを2つ紹介するよ。
これならどんな校舎がきてもイチコロさ。
まずは、
影で校舎の高さを求める問題を解説していくよ。
つぎの練習問題をといていこう。
この問題は3ステップでとけちゃうよ。
相似な図形をさがしてみよう。
影をつかう問題では、
の2つが相似になってるよ。
なぜなら、三角形の相似条件の、
2つの角がそれぞれ等しい
にあてはまるからね。
人と校舎は地面に対して垂直にたってるね。
だから、地面と接してる角度は90°。
ある時刻における、
地面と太陽の角度、
つまり、太陽高度はおなじだから、
の2つが等しいはずだね。
だから、
が相似なんだね。
つぎは相似比を計算してみよう。
2つの三角形の「影の辺の長さ」に注目してみよう。
それぞれ、
だったね??
2つの三角形の相似比は、
(人の三角形):( 校舎の三角形) = 0.8 : 12.5
になるはず。
相似比から校舎の高さを計算してみよう。
校舎の高さをx m とすると、
1.6 : x = 0.8 : 12.5
0.8x = 1.6×12.5
x = 25
になるね。
おめでとう!
校舎の高さゲットできたね。
おつぎは、
縮図で校舎の高さを求める問題だよ。
これは作図しなきゃいけないから、
を用意してね。
つぎの練習問題をといてみよう。
身長1.6mの人間が校舎から20m離れたところから、校舎の頂点をみつめています。
ちょうど校舎のてっぺんが水平方向から42°のところにみえるとします。
このとき、400分の1の縮図で校舎の高さを計算しなさい。
この手の問題はつぎの3ステップでとけちゃうよ。
まずは、
「人の目」と「校舎」がつくる三角形
に注目しよう。
この三角形の縮図をかけばいいんだ。
問題文では、
400分の1の縮図をつかえ
っていう指示だったね。
「校舎までの距離20m」を400分の1にすると、
5cm。
角度が42°の直角三角形をかいて、その高さをだせばいいってことだね。
まず定規で5cmの直線をかいてあげて、
分度器で42°をはかって直線をひいてみる。
あとは、直角三角形の直角が必要だから垂線をかこう。
コンパスを持ち出す。
そして、5cmのところで半円をかく。
半円と辺の交点にコンパスの針をおき、チョビ円をかく。
逆側の交点にも針をおき、チョビ円をかく。
チョビ円どうしの交点とはじめの半円の中心をむすべば直角のできあがり!
⇒くわしくは垂線のかきかたをよんでね
こんなかんじで、
角度42°の直角三角形の縮図がかけたね。
おそるおそる、直角三角形の高さをはかってみると・・・・
ん!?
4. 5 cm
じゃないか!
直角三角形の高さは、
校舎の高さを400分の1に縮めたもの
だ。
400倍して校舎の高さにもどそうか。
実際の校舎の高さ
= 4.5 × 400
= 1800 [cm]
= 18 [m]
になるね。
・・・・おっとあぶねえ。
これは、
人の目線〜校舎のてっぺん
までの距離だ。
「地面」から「人の目線」までの距離
をたさないとね。。
ひとの目線の高さをたしてやると、
18 + 1.6
= 19.6 [m]
になる。
これが校舎の高さだ。
おめでとう!
これで縮図で校舎の高さを求められたね。
相似の利用の校舎の問題はどうだったかな??
校舎の高さを2つの方法で計算できれば大丈夫。
テストに校舎の高さの問題がでても、相似を利用してやればどうにかなるのさ。
そんじゃねー
Ken