こんにちは!この記事をかいているKenだよ。ビタミンCがほしいね。
数学の証明を勉強していると、
仮定
とか、
結論
っていうムズい用語言葉がでてくるね。
日常生活で使わないから、
わけわからないよね??

そこで今日は、
「仮定」と「結論」という用語をわかりやすく解説していくよ。
よかったら参考にしてみてね。
〜もくじ〜
まずは仮定からみていこう。
意味を辞書(デジタル大辞泉)でしらべてみると、
1) 未定のこと、不確かなことを仮にこうと定めること。また、仮に定めた事柄。「今ここにコップがあると仮定してみよう」「仮定の上に立って物を言う」
2 ) 論理学などで、ある命題を導き出す推論の出発点におかれる前提条件。
ってかいてある。
数学の証明では2つめの意味がそれにあたるんだけど、正直よくわからないよね?。
あまりにも中学生にはむずかしすぎる・・・たぶん、大人にもむずい・・・
そこで、もう少し簡単にいってやると、
ある問題においてのみ、仮に正しいとされたこと
といえる。
えっ。これでもよくわらかないって!?
そうだな、たとえばつぎの問題があったとしよう。
例題
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
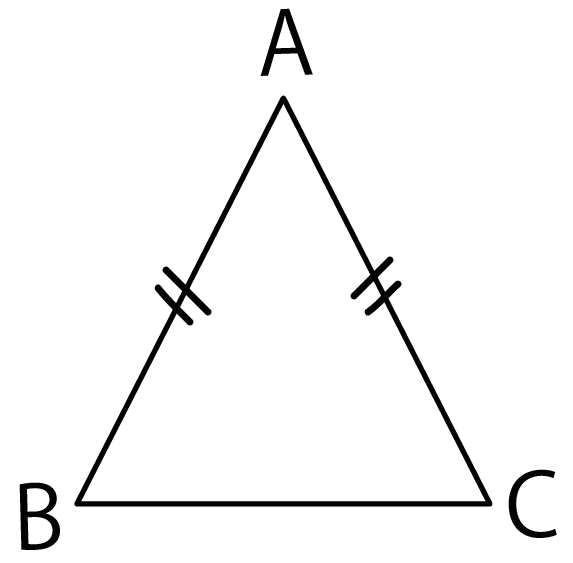
この問題のいっちゃんはじめに、
AB = AC である△ABCがあるとします。
ってかいてあるね。
じつはこの「AB = AC」はこの問題限定でいえること。
世界中に存在する△ABCのすべてが「AB = AC 」ってわけじゃあない。
AB = BCの△ABCもいるかもしれないし、
はたまた、
辺がぜんぜん等しくない△ABCもいるかもしれないね。
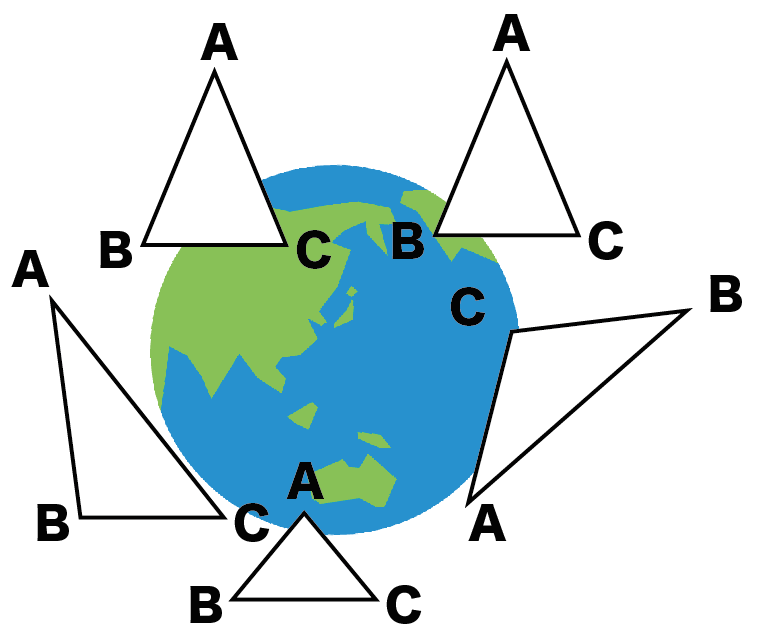
だから、
「AB = AC」は例題限定で正しいとしていることだから、
こいつは「仮定」なんだ。
どう?ちょっとスッキリしたかな?
結論は、
仮定をつかって正しいといえること
だよ。仮定がなければ結論をみちびけない。
たとえ、どんなに天才だとしてもね。
さっきの例題をみていみよう。
例題
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
この問題の仮定は、
AB = AC
だったね。
この仮定があるから、結論である「△ABCは二等辺三角形である」っていう結論がみちびけるんだ。
なぜなら、2つの辺が等しい三角形は二等辺三角形だからね。
もし、仮定がない問題だったら↓↓
例題
△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
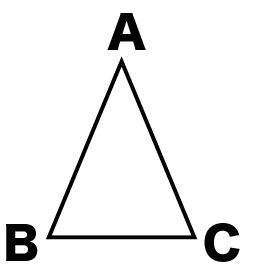
これはね、無理。無理だよ。
この問題には仮定がどこにもない。
△ABCが二等辺三角形であるって結論を導けるわけがないんだ。
「仮定」をつかってみちびける事実を「結論」という
ことをおぼえておこう。
「仮定」と「結論」は証明問題には必要不可欠なものさ。
なぜなら、証明とは、
与えられた仮定をつかって結論を論理的にみちびくこと
だからね。
「仮定」や「結論」がない証明問題はたとえるなら、
豚肉がない生姜焼きみたいなもんさ。
テスト前にもう一度復習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。トイレットペーパーに助けられたね。
中学2年生になると、
数学の証明
がはじまる。
いままでの数学では、
図形の面積をだしたり、
xにyを代入したりすればよかったね。
だがしかし、証明はそーはいかない。
ぜんぜんタイプが違うんだ。
むずいというか、うざい。
そんなタイプの単元だ。
今日はやっかいな証明を攻略していくために、
証明とはなにか??
ということを解説していくよ。
Wikipediaによると「証明」とは、
ある事柄が真理もしくは事実であることを明らかにすること
ってかいてあるね。
んでもこれじゃあ、よくわからない。
「数学の証明」って何を明らかにするんだろう??
って疑問に思うはずだ。
数学の証明とは簡単にいうと、
ある仮定(問題文であたえられている条件)が成り立つとしたときに
結論(証明のゴール)が正しいと明らかにすること
なんだ。
「仮定」から「結論」を明らかにするために、
いままでならってきた
「根拠となることがら」をつかっていくよ。
「根拠となることがら」ってたとえば、
三角形の合同条件とか、
対頂角は等しい
とかだね。
イメージでいうと証明は「カレー作り」に似ている。
仮定っていう「具材」を、
根拠のあることがらっていう「包丁」とか「鍋」で調理して、
結論っていう「おいしいカレー」をつくる
って感じ。
だから証明の問題では、
いかに多くのの「根拠となる事柄」(包丁や鍋)をつかって、
仮定(具材、ルー)から結論(カレー)をみちびくか??
がポイントなのさ。
つまり、
「根拠となることがら」をたくさん暗記すると有利ってことになるね。
証明の例を紹介するよ。
つぎの例題をみてみて。
例題
つぎの三角形ABCと三角形DEFが合同であることを証明してください。

まず仮定(問題文であたえられている条件)
と、
結論(証明のゴール)
を整理してみよう。
この問題の仮定は、
だね。だって、問題文がそう言ってるからさ。
んで、
結論は、
だ。
この2つの三角形が合同だってことをいえばゴールってわけ。
証明は基本的に、
の順番でかいていけばいいよ。
実際に例題の証明をかいてみるとこうなる ↓↓
△ABCと△DEFにおいて、
BC = EF = 6 cm
角B = 角 E = 60°
角C = 角F = 70°
よって、
1組の辺とその両端の角がそれぞれ等しい
ので、
△ABC ≡ △DEF
となる。
っていう感じ。
っていう順番になっていることを確認してね^-^
証明ってはじめてきくと、むちゃくちゃむずそう。
でも大丈夫。
証明なんてただの「カレー作り」さ。
「仮定」っていう具材を、
「根拠となる事柄」をつかって調理して
「結論」っていうカレーをつくってあげよう!
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよー。コーヒーは何度飲んでもうまいね。
「円とおうぎ形」という単元では、
という2つの図形について勉強していくよ。
前回まで、
っていう2つの公式をマスターしてきたね。
今日は、「扇形の面積」について詳しく勉強していこう。
「面積の求め方の公式」をおぼえていればテストでも楽勝さ。
~もくじ~
「おうぎ形の面積の求め方」はつぎの公式であらわされるんだ。
半径をr、面積をS、円周率をπ、中心角をαとすると、
S = πr² × α / 360
になるんだ。
つまり、
円周率×半径×半径×中心角÷360
ってわけさ。
たとえば、半径3cm、中心角が90度の扇形があったとしよう。扇形の公式をつかってやれば、
S = 3×3×π×90/360
= 9π/4
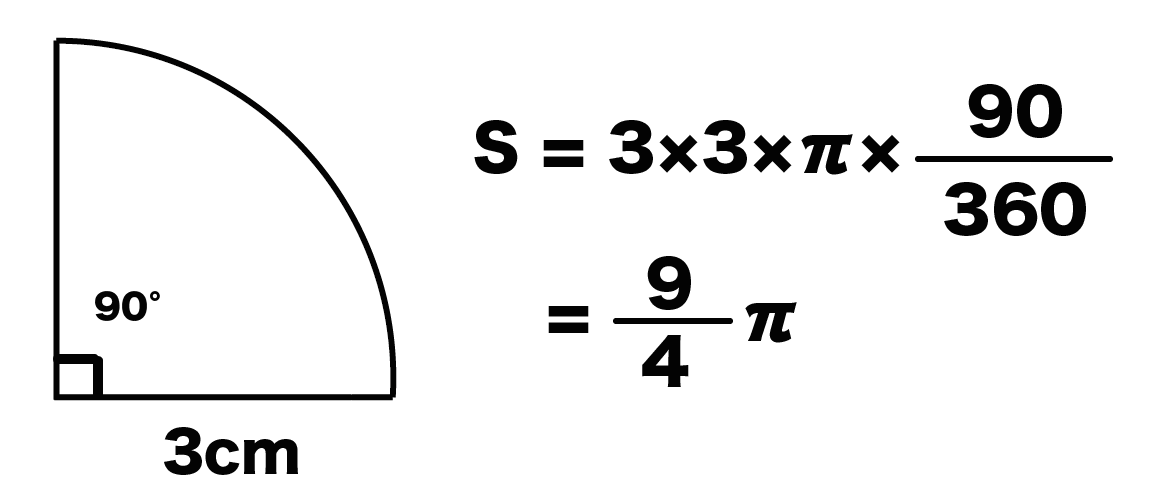
になるんだ。どんな扇形の面積でもバッチコイだね!!
扇形の面積の求め方はあんまり難しくない。シンプルさ。
ただ、半径rの「円の面積」に「おうぎ形パワー」をかけているだけなんだ。
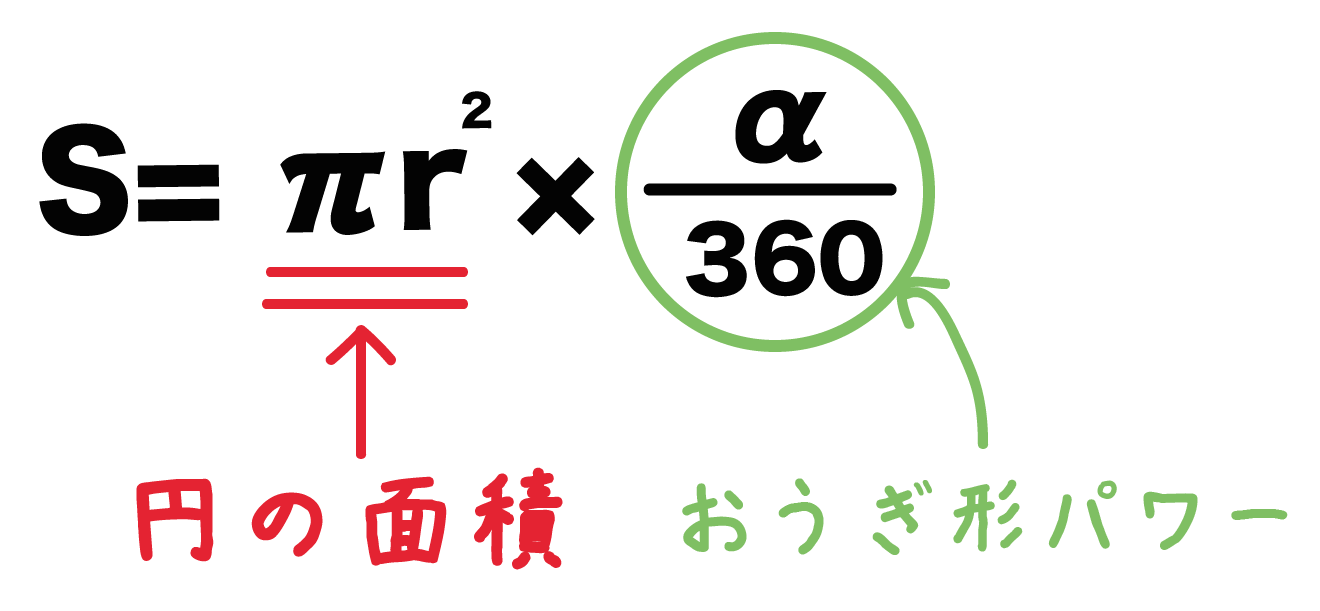
ここでいう「おうぎ形パワー」っていうのは「扇形の大きさ」をあらわしている指数のことさ。
扇形が大きければ大きいほど大きくなる。
おうぎ形パワーとは、
「同じ半径の円」に対して「扇形」がどれくらいの割合になっているか??
ということを表したものなんだ。
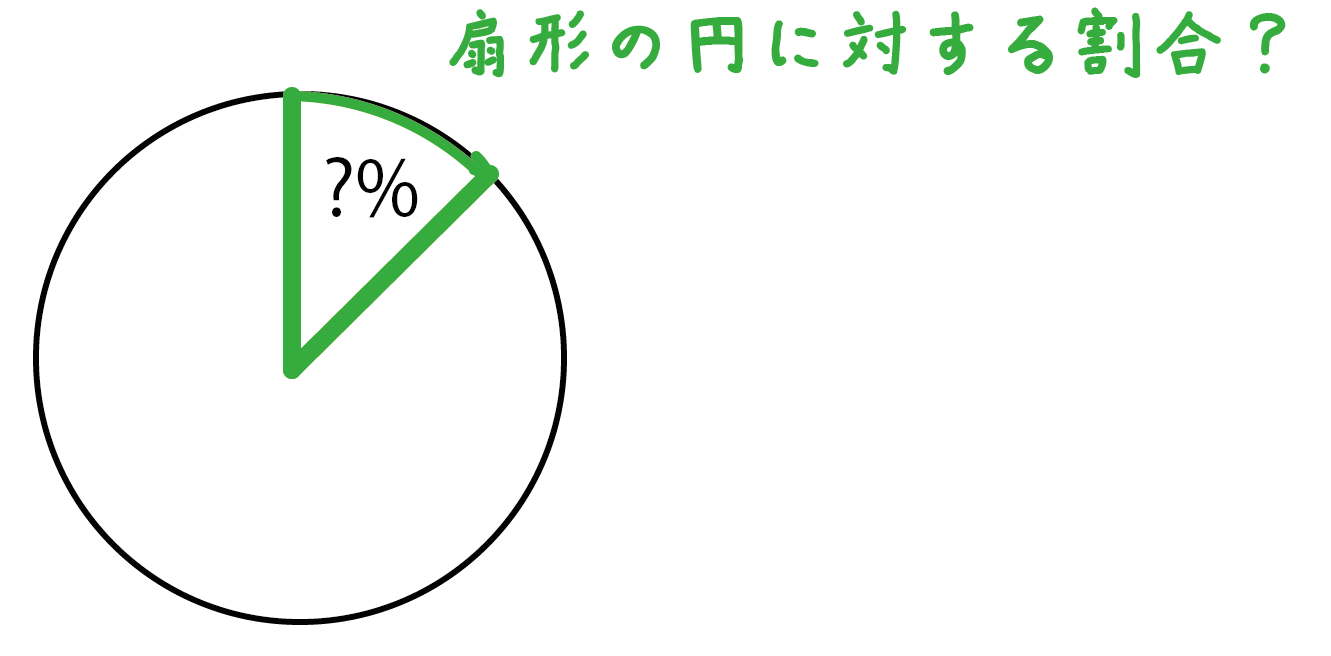
この割合を計算するためには、
「扇形の中心角」が360°中どれだけ大きいか??
ということをみればいい。だって、円の中心角はぐるっと回った360°だからね。
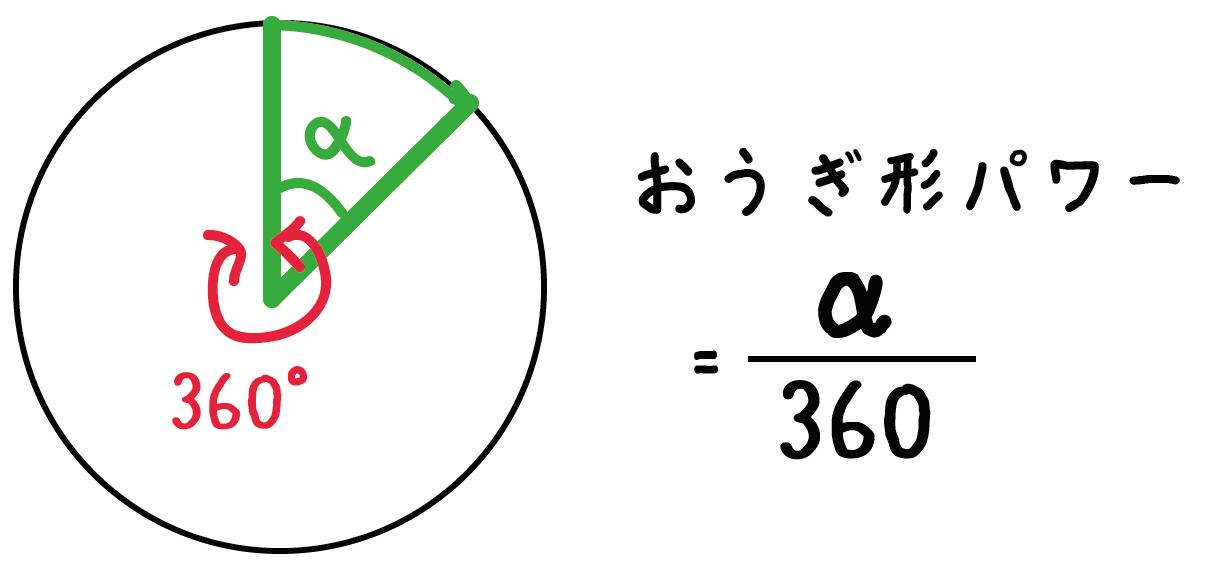
だから、おうぎ形パワーは中心角αを360°でわった、
α/360
になるんだ。
これはなんという偶然か、ピザを切り分けるときと一緒。
一枚まるまる1200kcalのピザがあったとしよう。こいつを6枚に切り分けると、カロリーはその1/6の200kcalになるでしょ??
これは一枚のピザにたいしてどれぐらいの大きさをしているか、ということを表しているんだ。
「扇形の面積の公式」を忘れたら「ピザ」を思い出そう。
扇形の面積の求め方はどうだった??
円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。
S = πr² × α / 360
「円とおうぎ形」がテストにでるときに確認したいね。
おうぎ形の面積をマスターしたら次はおうぎ形の中心角を求めてみよう!
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。コーヒーは一日一杯までだね。
中1数学の平面図形で勉強する図形の移動には、
の3種類があるって勉強してきたね。どれもテストで狙われやすいやつばっかだけど、一つ一つ順番にみていこう。

今日は2つめの「回転移動」の書き方をわかりやすく解説していくね。
テスト前に参考にしてみてね。
回転移動では回転移動の性質を使うと一発で終わるんだ。
教科書によると、
対応する点は、回転の中心からの距離が等しく、回転の中心と結んでできた角の大きさはすべて等しい
という性質があるって書いてある。
これはどういうことなんだろう??
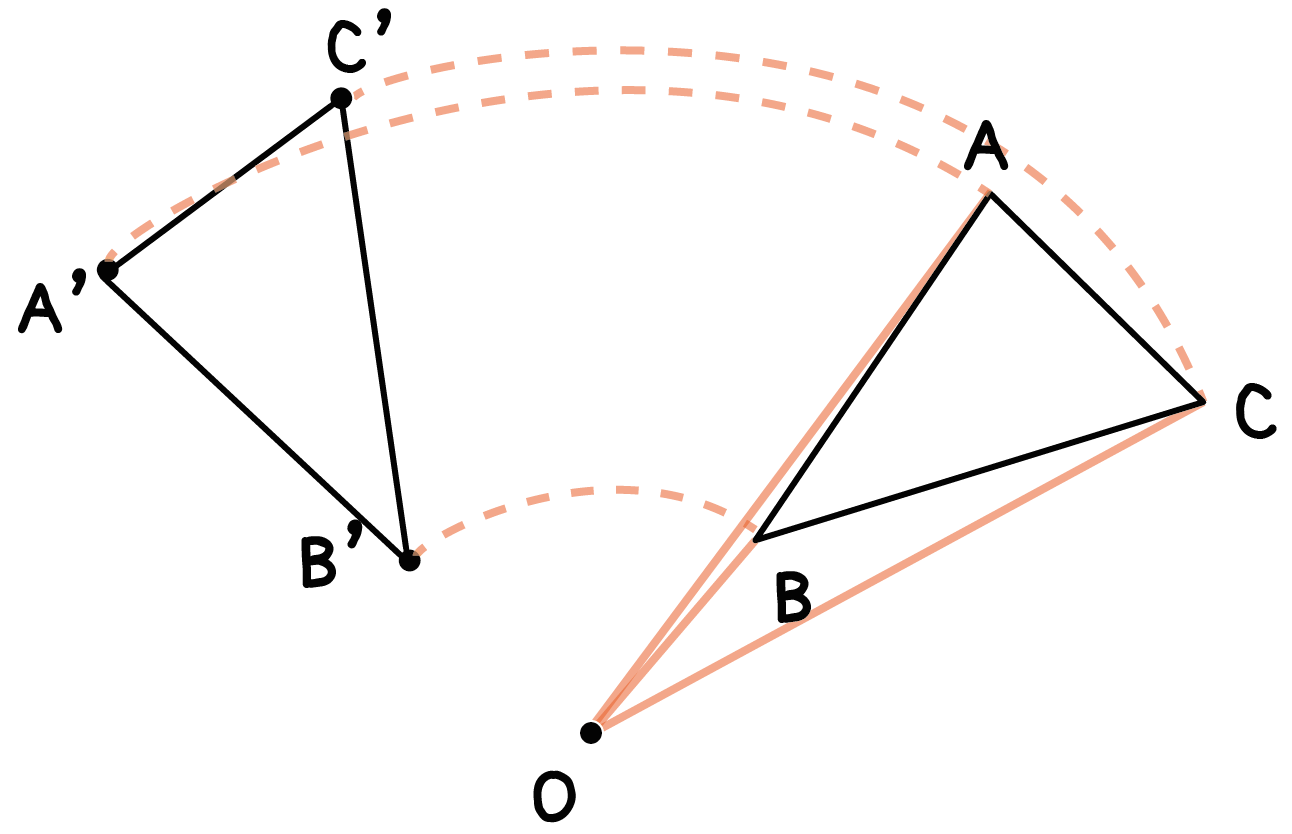
たとえば、点Oを「回転の中心」として三角形ABCを回転移動させてやるとしよう。
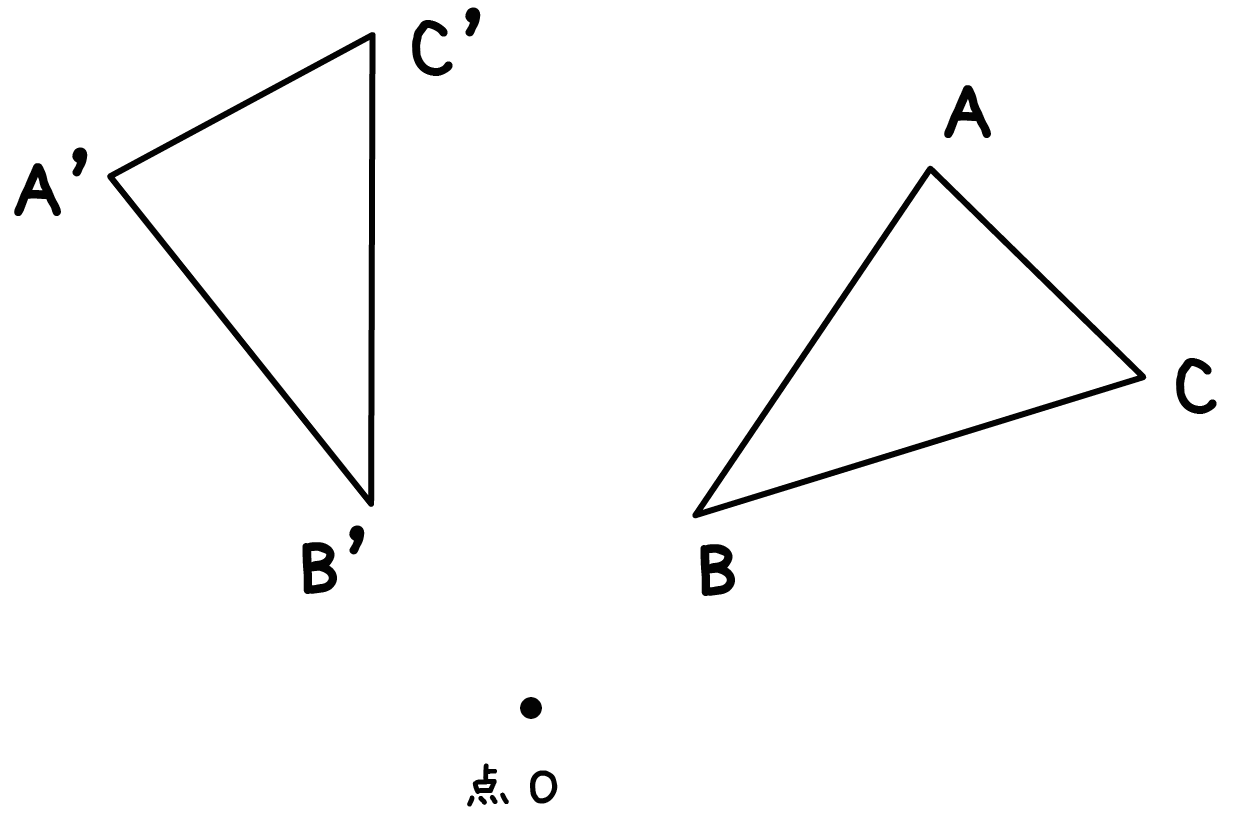
このとき、対応する点BとB’は、
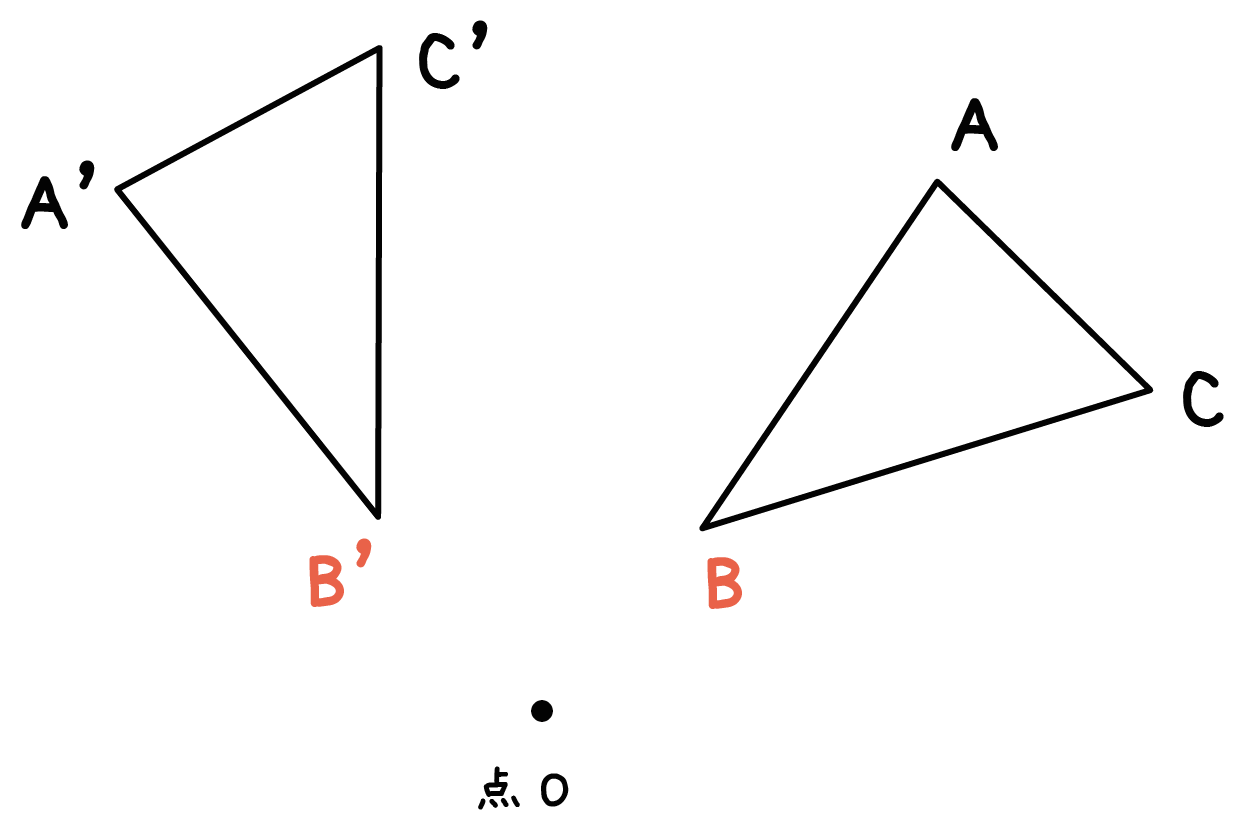
回転中心Oからの距離が等しい ( 線分OB=線分OB’)。
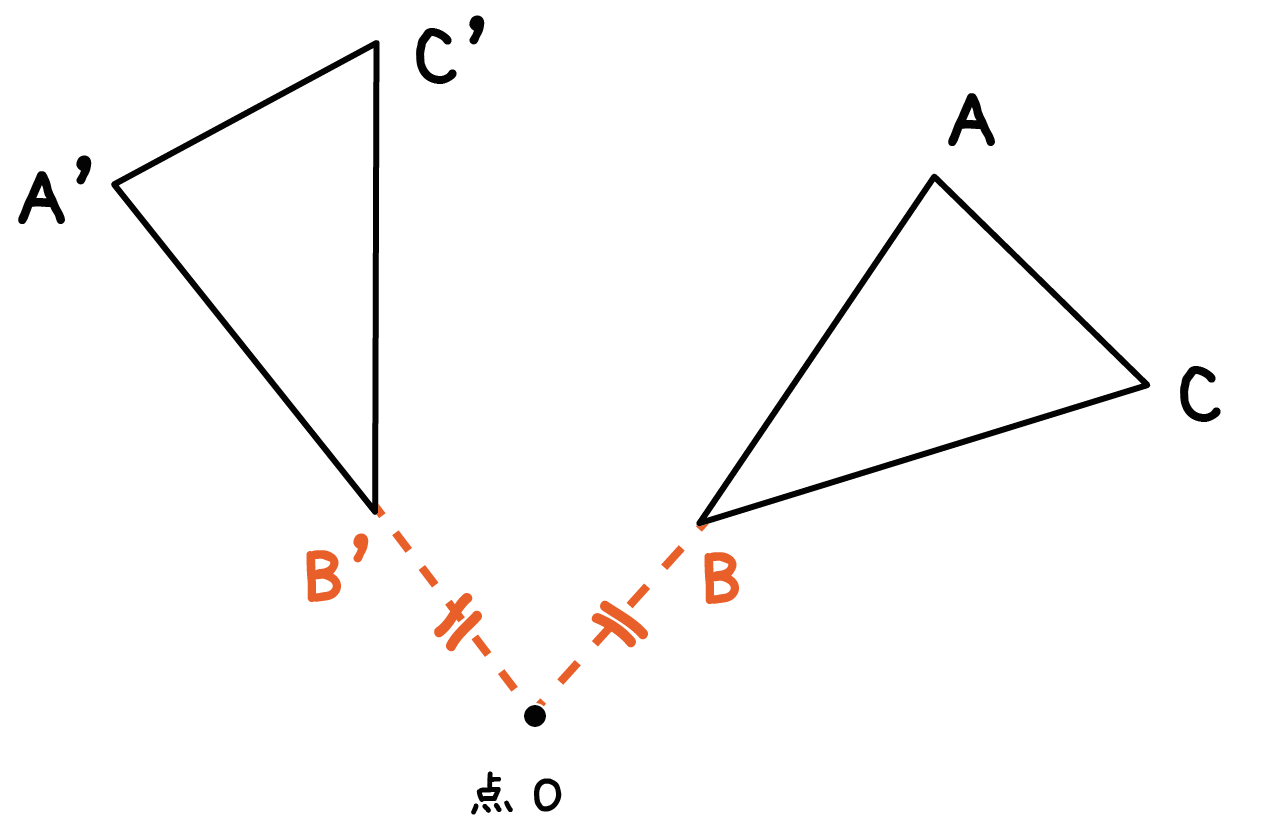
さらに、回転の中心と結んでできた角の大きさ(角BOB’)は、
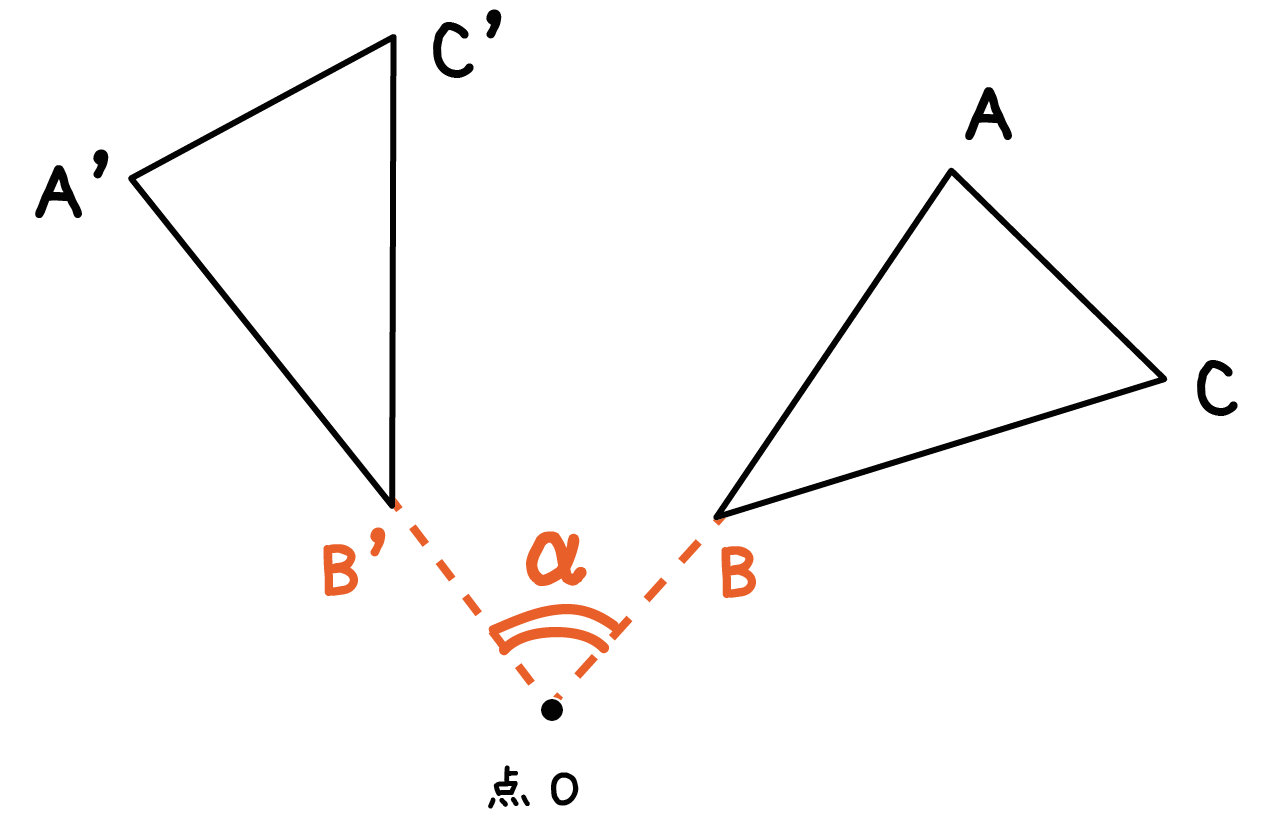
他の頂点の場合のそれとすべて等しい (角BOB’ = 角AOA’ = 角COC’)ってことなんだ。
これが回転移動した図形の性質だね。
こいつらをウマくつかってやれば、自由自在に回転移動できるようになるよ。
それじゃあ、さっそく回転移動の書き方を解説していこう。
よーくみてみると、回転移動はつぎの5つのステップで書けることがわかる。
「回転の中心」と「1つの図形の頂点」を結んであげよう。
そして、あたらしい線分をつくってあげるんだ。
たとえば、
三角形ABCをOを中心に反時計まわりに90°回転移動させよ!
っていう問題があったとしよう。
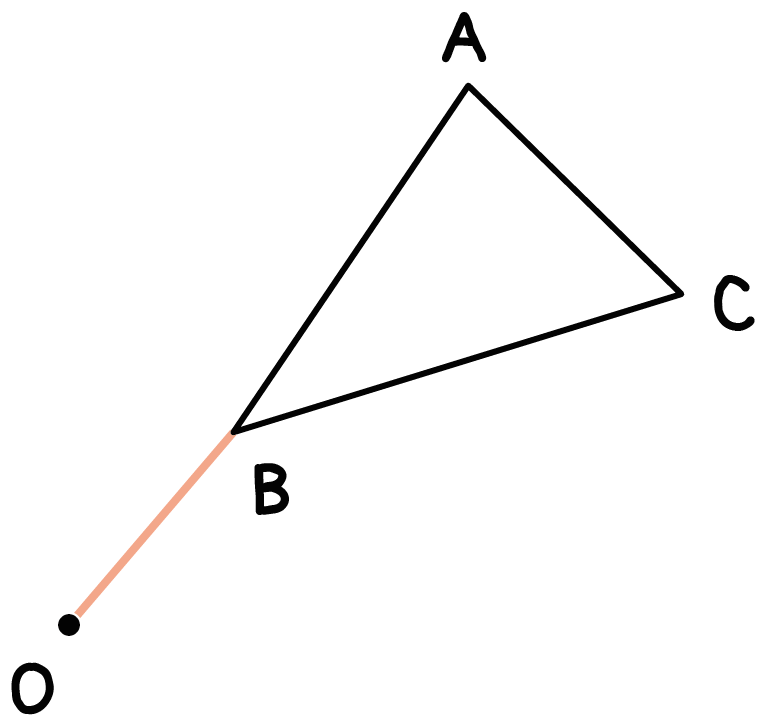
この場合なら、OとBを結んで線分をOBをつくってあげるって感じ。
これが第一ステップさ。
つぎは、コンパスの出番だ。
ステップ1でつくった線分を半径として、回転の中心から「孤」を書いてみよう!
コンパスの針を「回転の中心O」において、
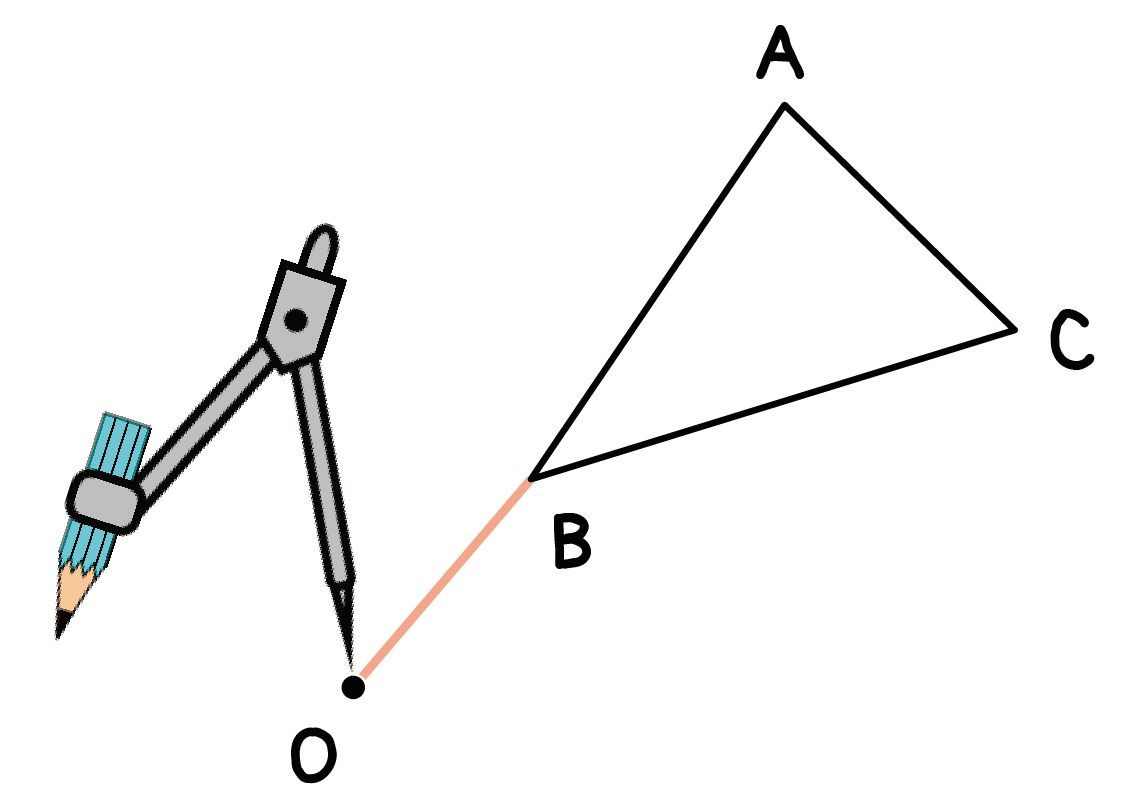
コンパスの鉛筆側を頂点Bにあわせ、
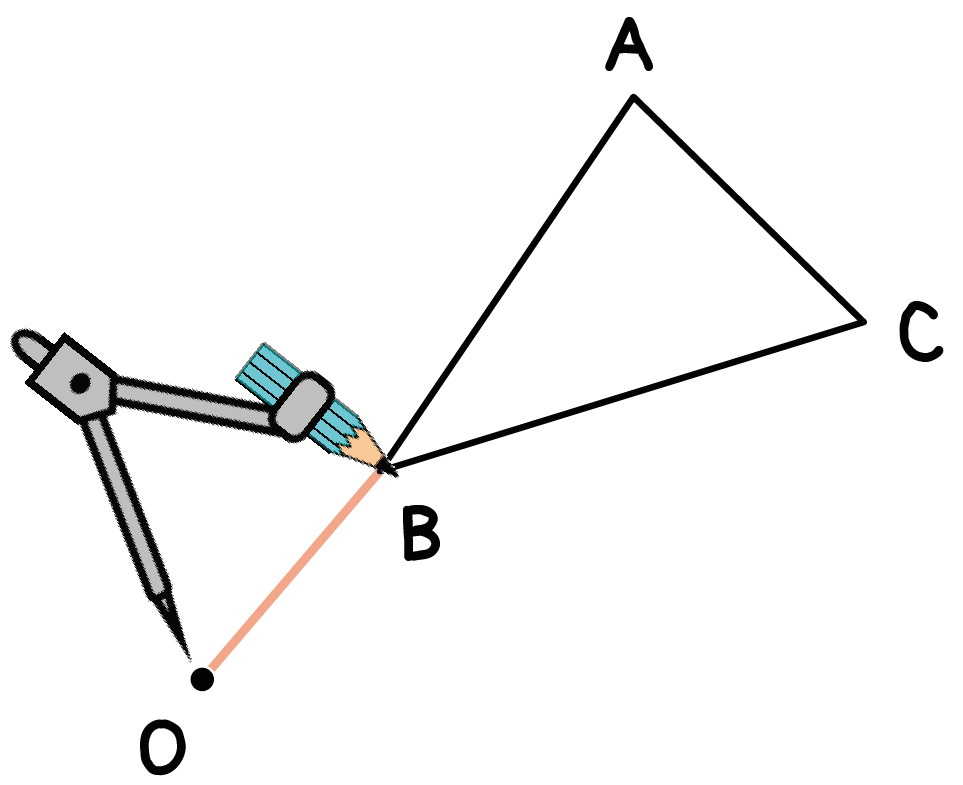
反時計回りに90°以上の孤をてきとーに書いてあげよう。
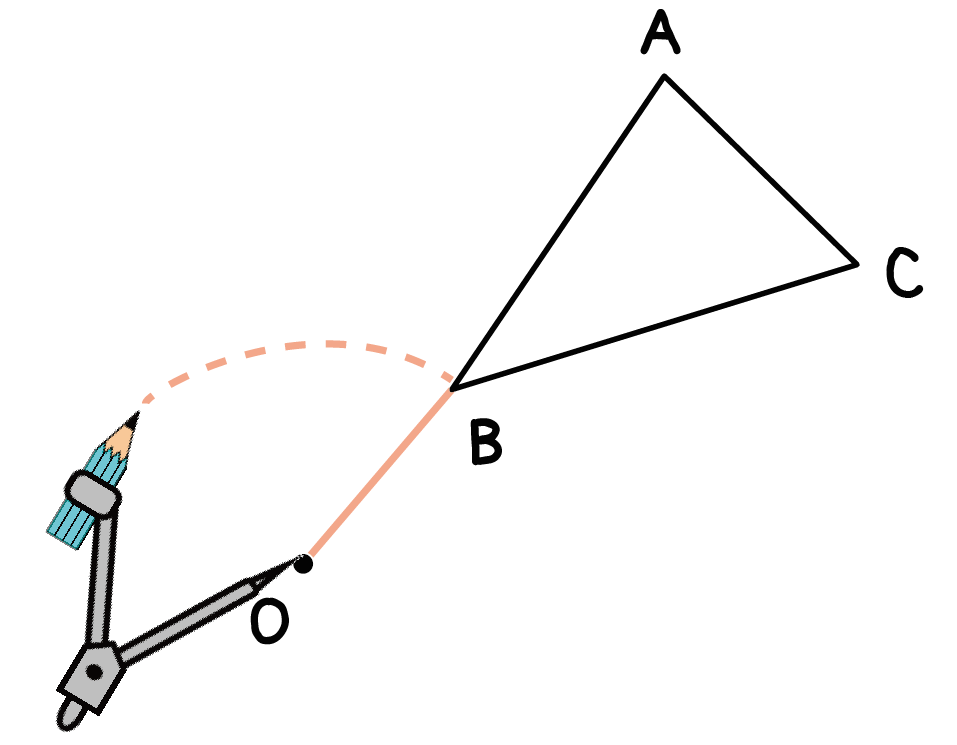
つぎは、回転させる角度をはかっちゃおう。
この例題では、反時計まわりに90°図形を回転移動させる問題だから、
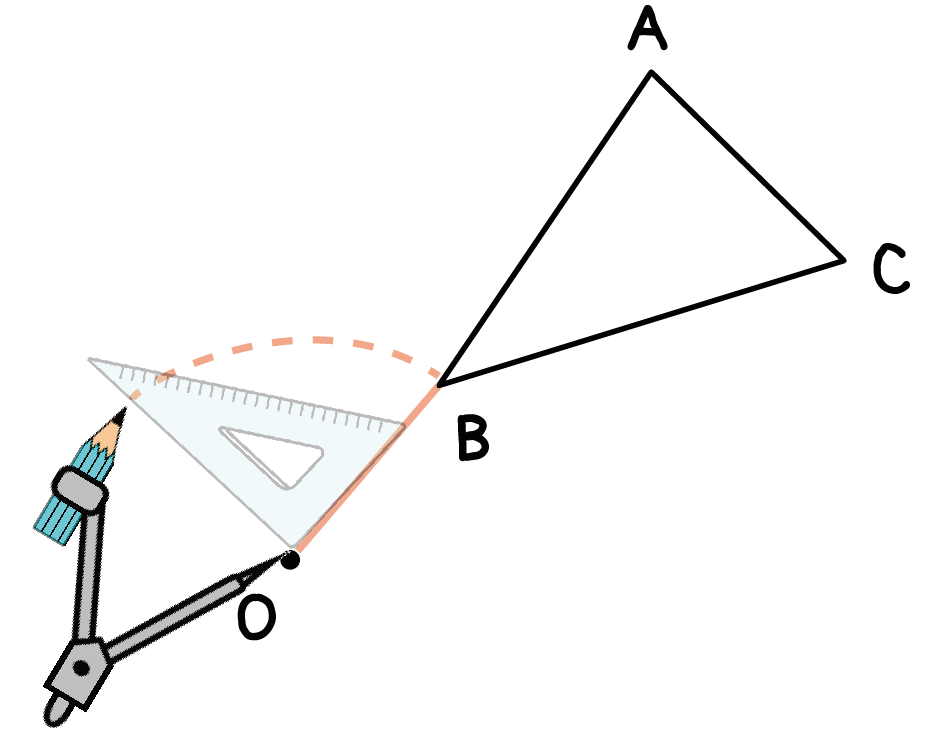
孤の半径となっている線分OBから反時計回りに90°の角度をはかってあげよう。
角度を測る方法としては、
などがあるよ。もし、分度器を使うな!って問題でいわれたら、三角定規とコンパスでねばってみよう!!
回転させる角度を測った??
あとは、その角度上の孤に「点」をうってあげるだけ。
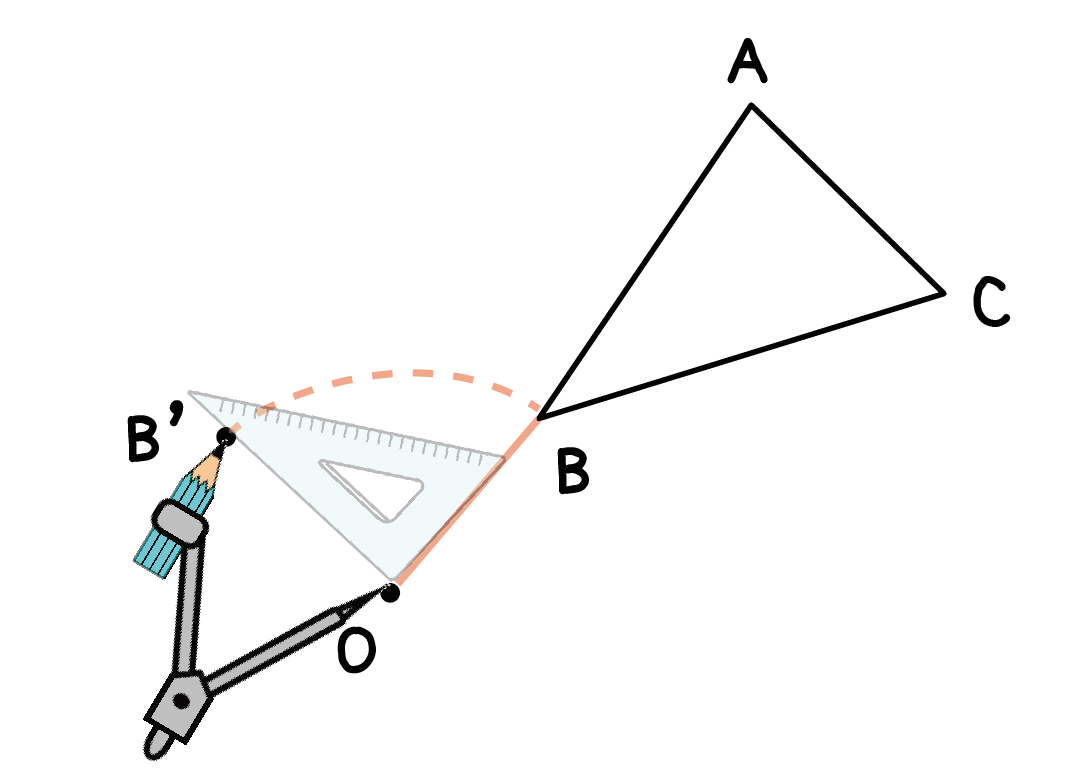
さっきの例でいえば、
孤の90°の角度上に点B’がうてる。
同じ手順をのこりの頂点でもやってみよう。
この例題だと、点AとCだ。
点Bと同じように、
という動作を繰り返せばいいんだ。
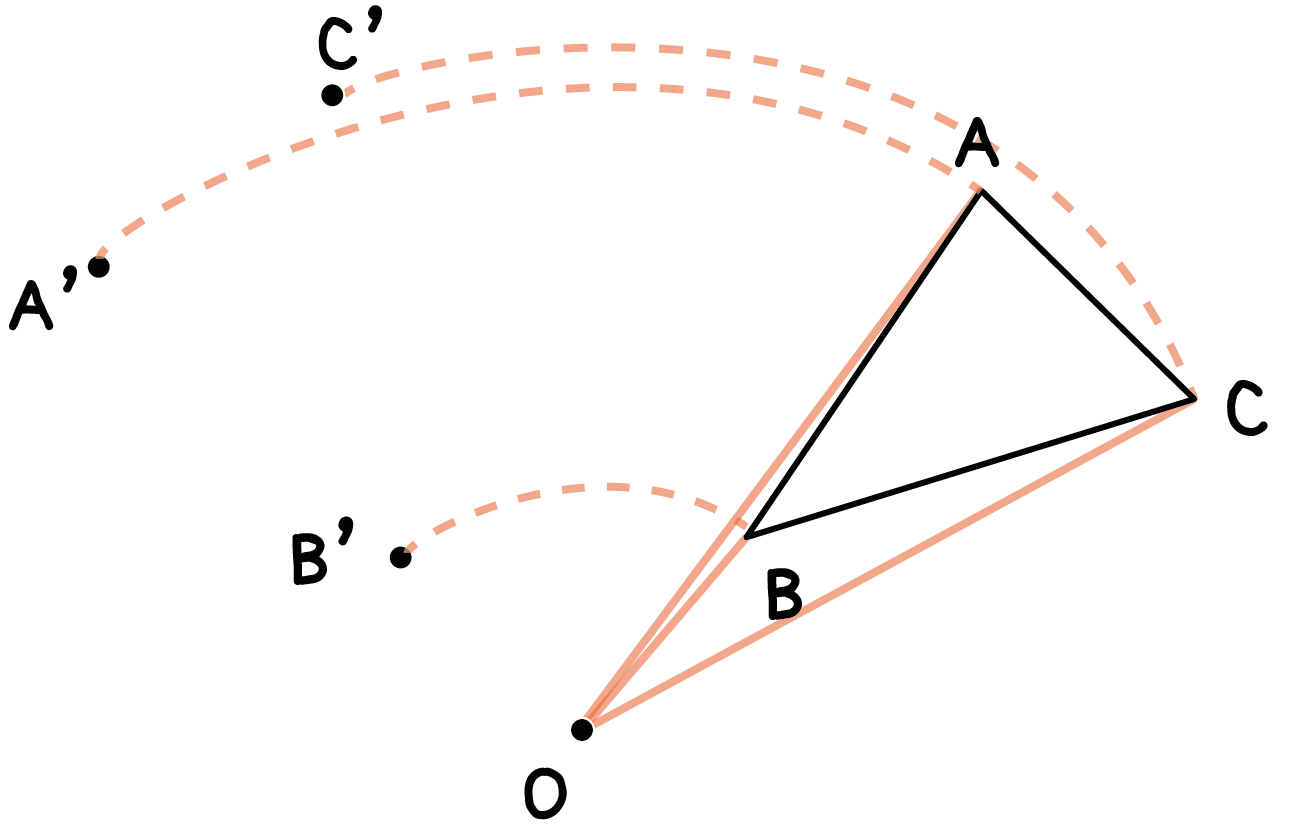
そんで、ぜんぶ書き終えたら結んでみよう!
この新しくできた三角形A’B’C’が「回転移動した図形」だ!
やったね! 疲れたー
回転移動の書き方はどうだった???
コンパス、三角定規、分度器っていう3つのアイテムでチョちょいのちょい。
テストでも落ち着いて図形を移動させていこう!
次回は対称移動の書き方を解説していくね。
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。メガネふきが欲しいね。
「図形移動」の方法って次の3つあったよね。
こいつらを「【中1数学】平面図形で勉強する「図形の移動」3つのまとめ」でだいたい確認してきたけれど、図形の移動を知っているだけじゃ問題は解けない。
じつは、
作図方法を知っていないとテストで点数はとれないんだ。

だから今日は、
平行移動の書き方・作図
をわかりやすく3つのステップで解説していくね。テスト前に参考にしてみてね。
~もくじ~
平行移動のために使うことはたった1つ。
それは、
平行移動した図形の性質だ。
平行移動した図形同士には、
対応する点を結んだ線分は、それぞれ平行で、その長さは等しい
という性質があるね。これは教科書にのっていることだ。
たとえば、三角形ABCを平行移動させたとすれば、
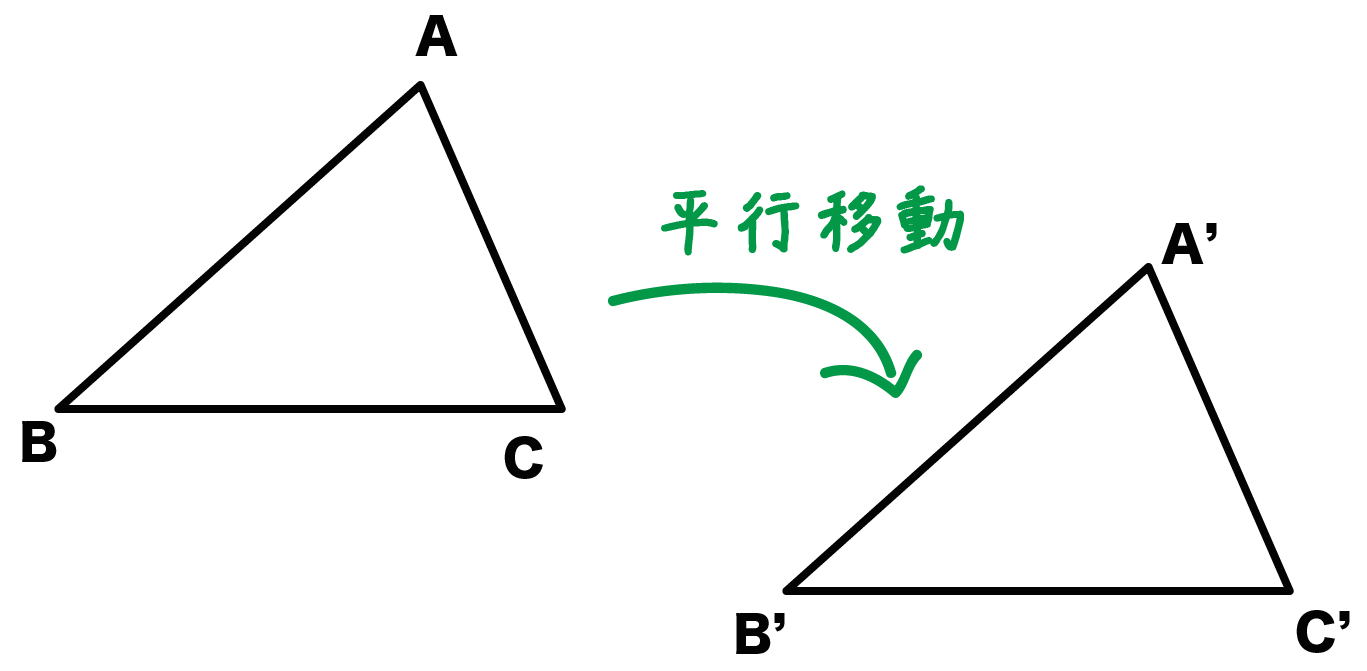
対応する点同士である、
を結んだ線分たちは、
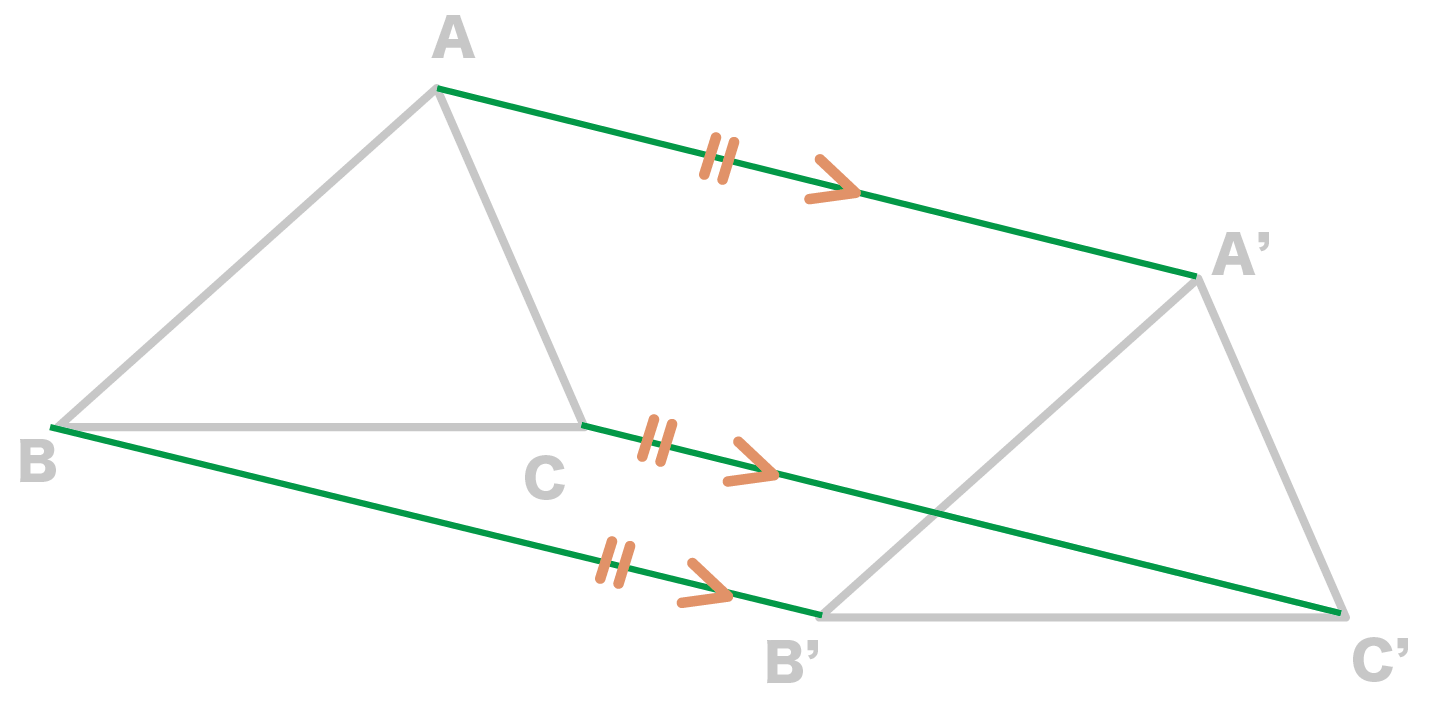
という性質があるんだ。
これをつかえば作図がつぎの5ステップでできるよ。
つぎのような作図問題が出されたとしよう。
問題:三角形ABCの頂点Aを点Pに移すように平行移動した図をかいてね。
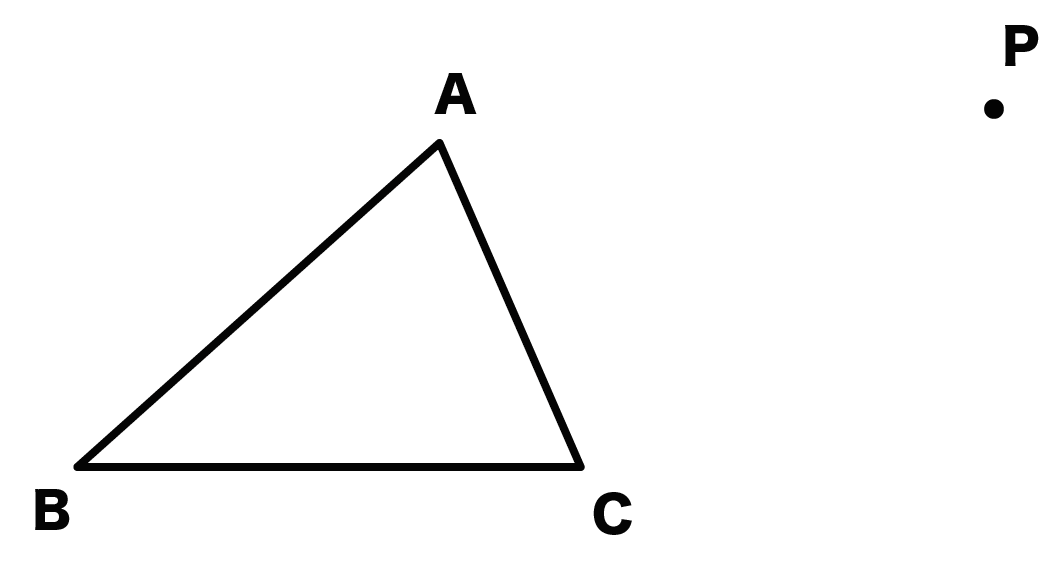
これをもとにしながら平行移動の書き方を解説してくね。
まず、対応する2つの点を結んでしまおう!
ここでいう「対応する点」とは、
「移動する前の点」と「移動後の点」
のことだ。さっきの問題でいうと、点Aと点Pがそれにあたるね。
ってなわけで、
対応する点AとPをむすんで線分APをつくっちゃおう!
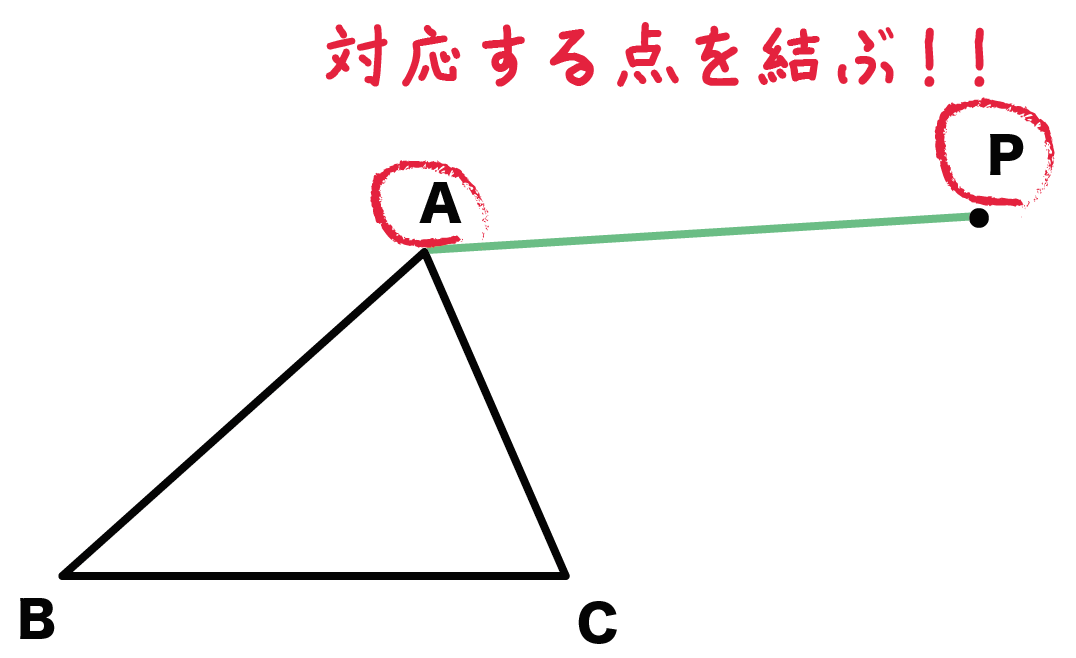
これが平行移動の作図の第一ステップさ。
次に、さっき引いた線分の平行線を残りの頂点からひいてあげよう!
この問題では点BとCから線分APとの平行線をひくってことだね。
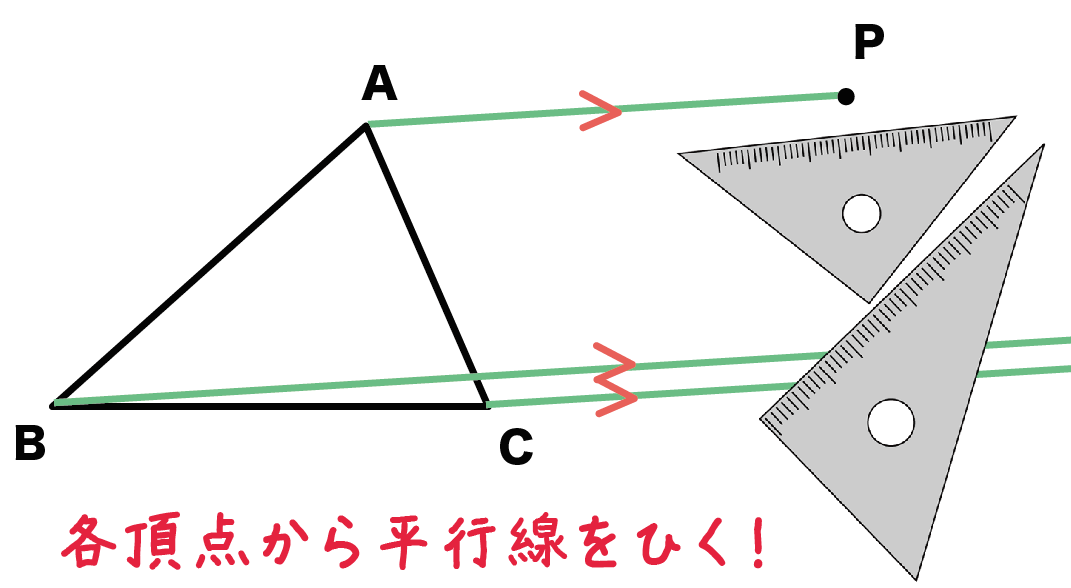
平行線をひくときはコンパスでも三角定規でもかまわない。
ただ、勘やひらめきで平行線をかかないようにしよう。
>>平行線の書き方はコチラ!!
つぎに、対応する点を両端とする「線分の長さ」をはかろう!!
ここでは線分APの長さってことだね。
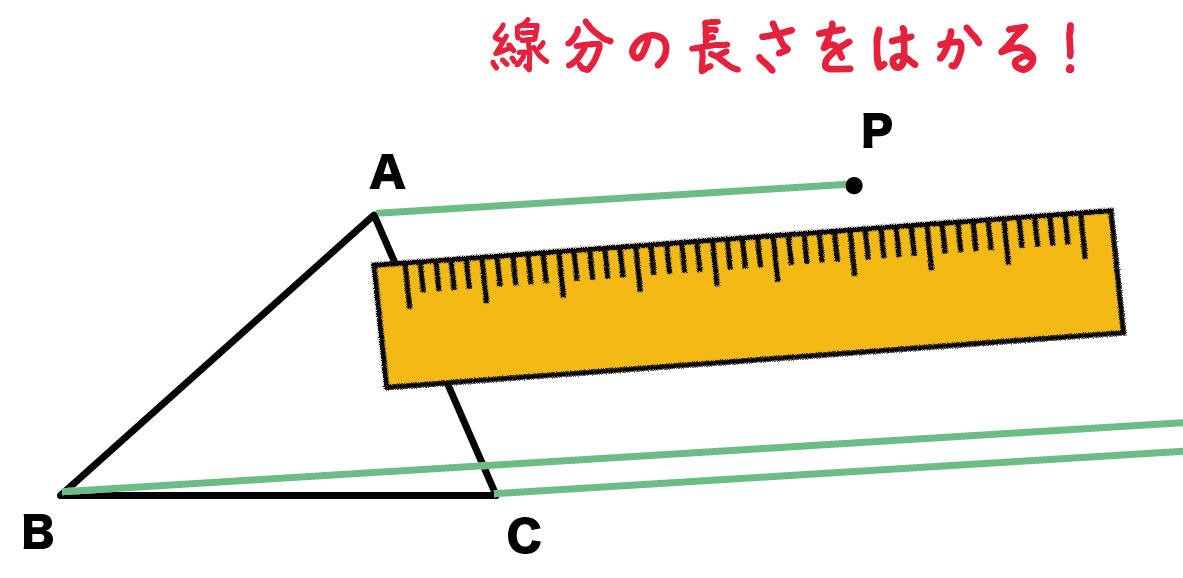
新しくできた線分に定規をあてるだけ。ゆっくり落ち着いてね。
ステップ3で測った長さを使うよ。
平行線上に、各頂点からその長さ分はなれたところに点をうつんだ。ちょっと言葉じゃ説明しずらいから下の図をみてくれ。
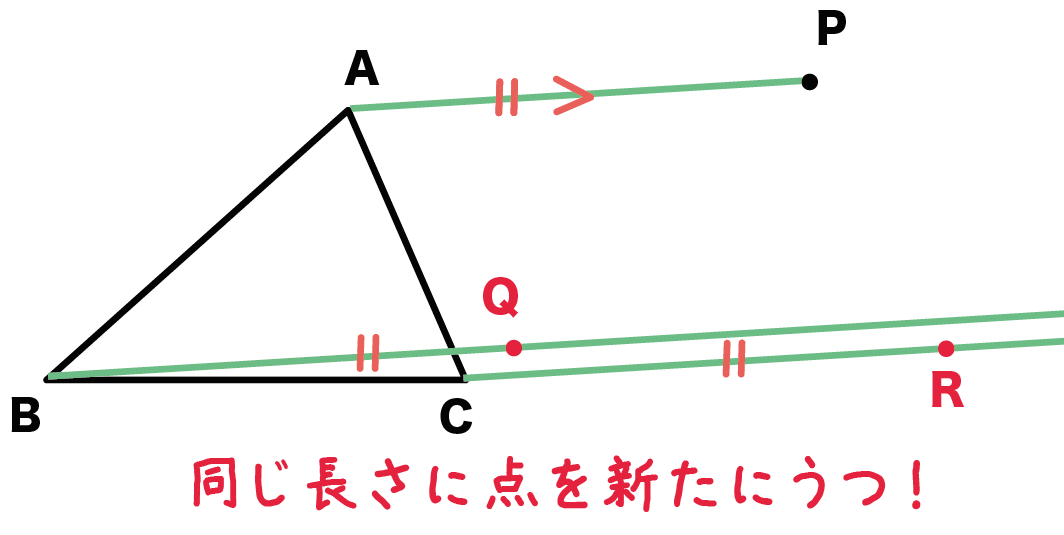
つまり、
AP = BQ = CR
となる新しい点Q・点Rを2つの平行線上にうつんだ。
これが第四ステップ。あと1つだね。
最後のステップはとってもカンタン。
ステップ4まで苦労して打ってきた点同士を結ぶだけだ。
さっきの例でいうと、
だね。そんで、点Pはもともと問題であたえられていた移動後の頂点。
だからこれも結んであげる。
そうすると、
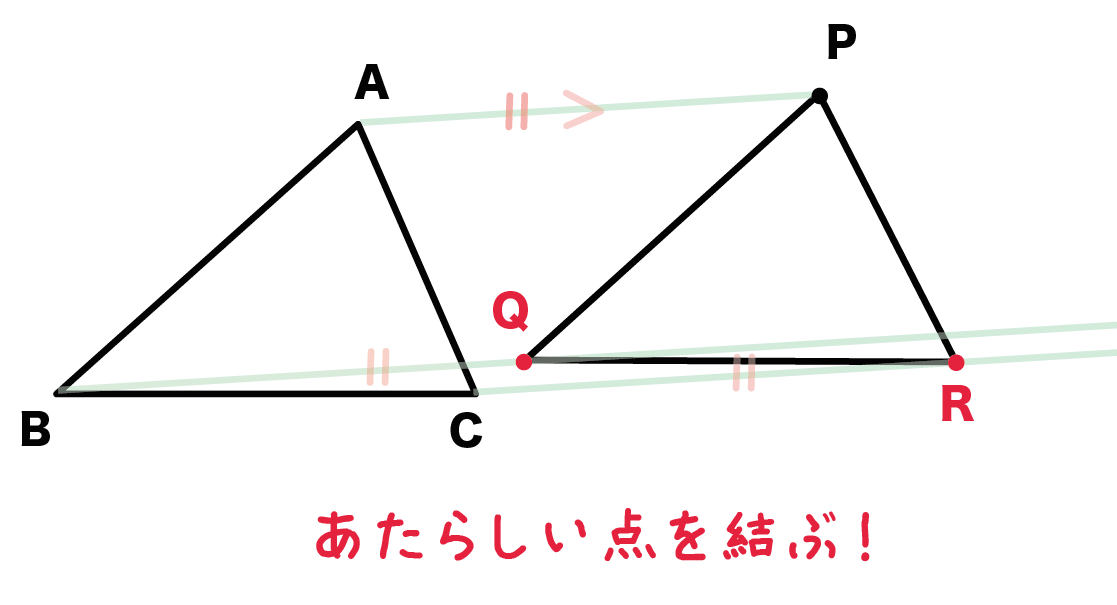
こんな感じで、
平行移動した三角形PQRが書けるんだ。
案外、平行移動の作図もカンタンそうでしょ!??
ここまでみてきた平行移動の作図はどうだった??
5つのステップでゆっくりかけば大丈夫。
あせって間違えるより確実に問題に答えたいね。
つぎは「回転移動の作図」について解説してくねー!
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。カピバラと温泉に入りたいね。
いよいよ中1数学の「平面図形」という単元にはいっていくよ。
いままで方程式とか関数とか勉強してきたけど、こっからは新しい「図形」というモンスターとたたかっていく。

今日は、「平面図形」という単元を楽に勉強するための、
中1数学の平面図形の攻略のコツ
を3つ紹介していくね。平面図形が苦手で泣きそうなときに参考にしてみてくれ。
つぎの3つのコツを押さえてしまえば平面図形がむちゃくちゃ楽勝になるんだ。
中1数学の「平面図形」の最大の特徴は、
図形の専門用語がたくさんでてくる
ということさ。
たとえば、
・・・・などなど。
数え始めればキリがない。平面図形という単元となかよくなるためには、まずはこれらの「図形ことば」を覚える、少なくとも馴れなければならない。
えっ。暗記が苦手だって!??
そういうときは、とりあえず楽な気持ちで進み続けよう。勉強していくうちに新しい言葉になれていくから大丈夫!
中一数学の「平面図形」では、図形を作図する問題がでてくる。
作図ってつまり、
図を自分で作る
ってことさ。

とくに教科書にどっさり載っている、
という3つはしっかりと押さえておきたい。これは期末・中間テストでねらわれやすいし、入試問題ではこれらを応用した問題がどしどし出題される。
中1数学の作図は一度マスターしちゃえばこっちのもの。
あとは何度も作図の練習を繰り返せばいいんだ。
作図をマスターすると人気者になりそうな気もするし、やっておくに越したことはないね。
中1数学の平面図形で最後にやることは、
図形のスペックを計算することさ。たとえば、円の面積とか三角形の面積の計算とか・・・・だ。
人間だって体重計で太っとかどうか調べるでしょ?? それと同じさ。
このダンジョンをクリアするためには、
という2つのソードが必要になってくる。
教科書にでてくる図形の公式をちょっと覚えて、算数でつちかった計算能力を発揮するだけ!!
これで平面図形の計算問題は大丈夫。きっと無傷でダンジョンから脱出できるはずさ。
中1数学の平面図形は、中学校で勉強する図形のほんの入り口。
ここでつまずいて血を流さないように、
という3つのコツで乗り切っていきたいね。
次回は線分について解説していくね。
そんじゃねー
Ken