Dr.リードだよっ。
円周角の定理の使い方にも慣れてきたかな?
今日はな、
円周角の定理の証明
を解説していくぞ。
つまり、
なぜ、円周角の定理が使えるのか??
ってことを暴いていくわけだ。
別に知らなくてもいいけど、知っておいた方がスッキリするだろ?
今日は長い長い話になる。
ピザでも食べながら行ってみよう!


「円周角の定理」を証明していくぞ。
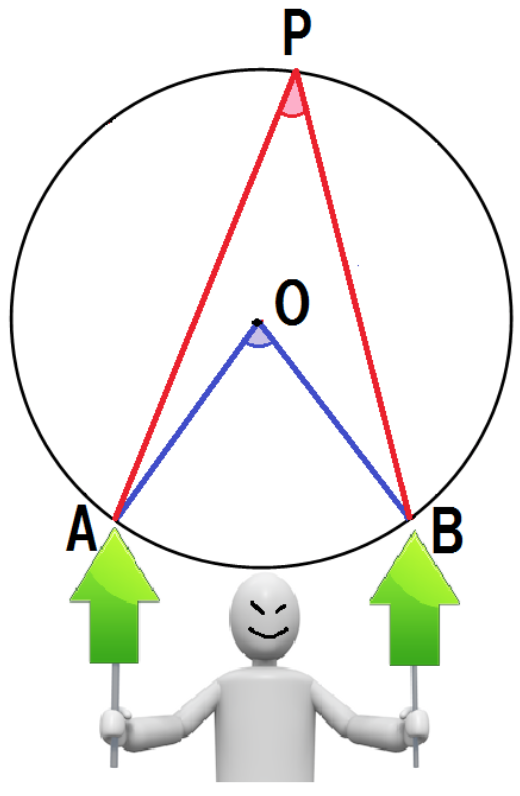
3点A・B・Pがある円Oを想像してくれよな。
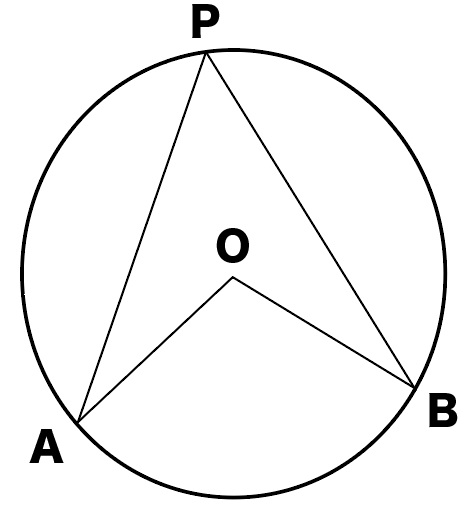
円周角と中心角の位置関係はつぎの3通りある。
それぞれの場合を証明していけばいいんだ。
まずは点P がOBの延長上にきてる場合ね。
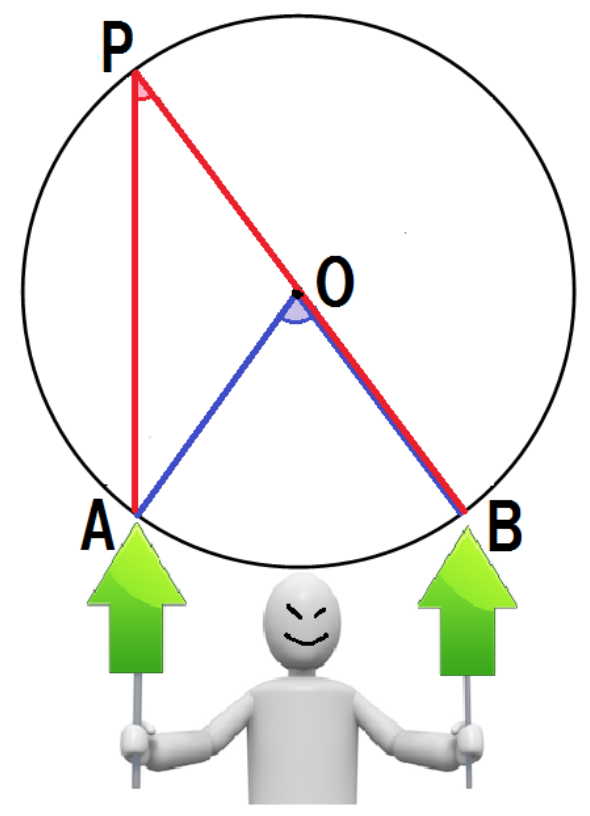
このパターンでは、
をうまく使っていくよ。
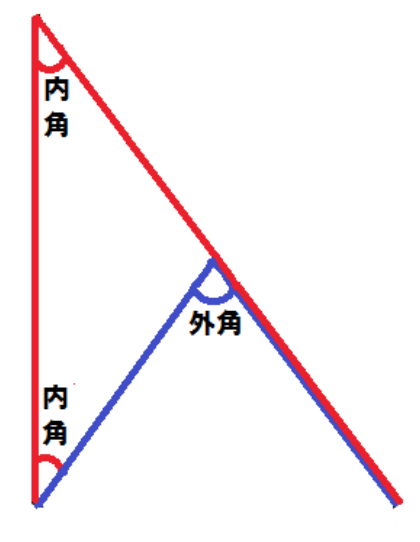
えっ。三角形の外角の定理なんて忘れた?!
三角形の1つの外角はそれと隣り合わない2つの内角の和に等しい
っていう定理だったね。
こいつをうまく使って証明してみよう。
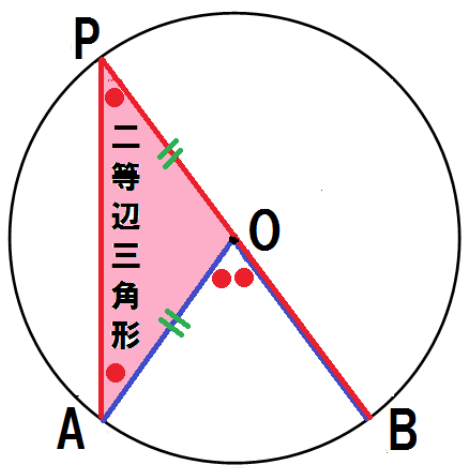
OP・OAはそれぞれ円Oの半径だから、
OP = OAよって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)三角形の外角の定理より、
∠AOB = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APB = 1/2∠AOB
「二等辺三角形の性質」と「外角の定理」を知ってれば証明できるね!
さあ、サクサク行くぞ。
つぎは、
中心Oが円周角の内部におさまってる形だ。
補助線を緑で引いていくぞ。
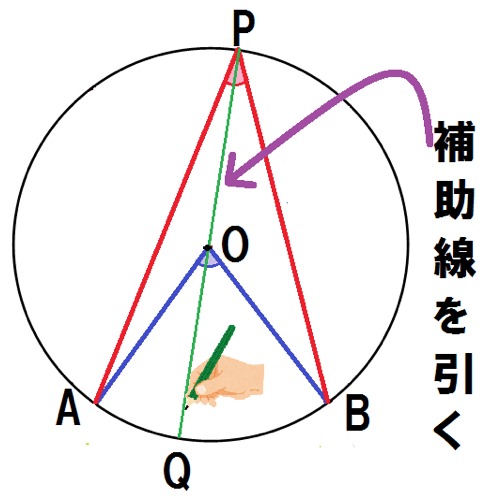
点Pと中心Oを結び延長して、交点をQとしよう。
中心を通るから、PQは円Oの直径ってことになるね。
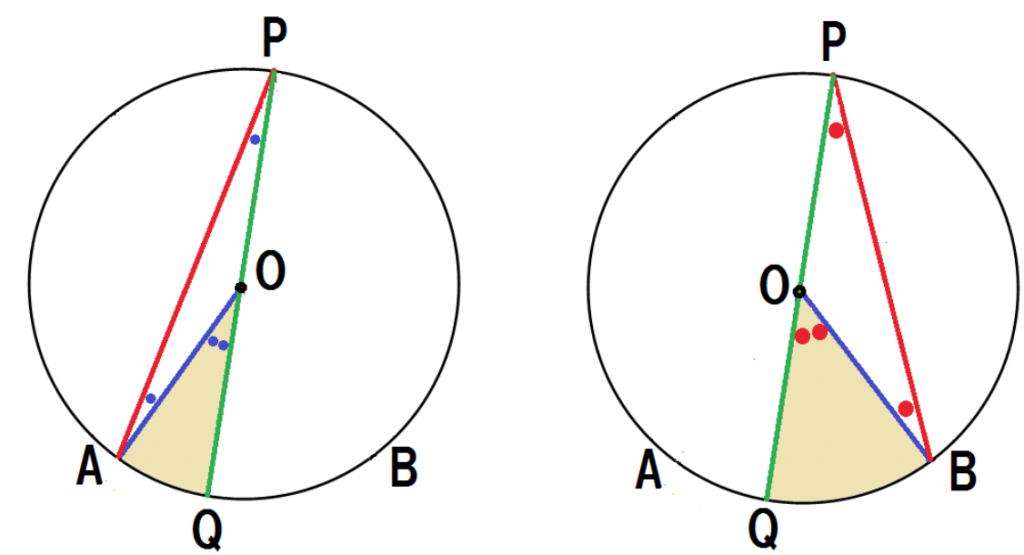
上の図みたいに補助線を中心に2つの図形に分けてみて。
の順番で証明していくよ。
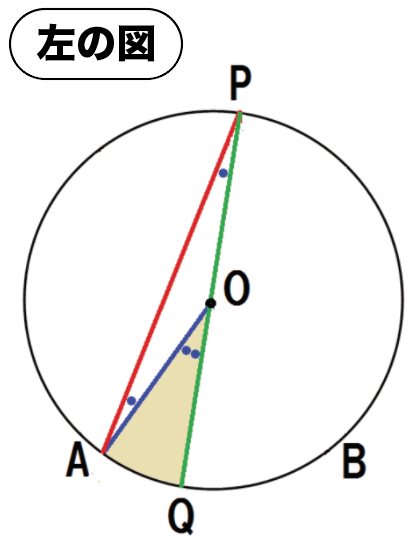
OP・OAはそれぞれ円Oの半径だから、
OP = OA
よって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)
三角形の外角の定理より、
∠AOQ = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APQ = 1/2∠AOQ・・・(3)
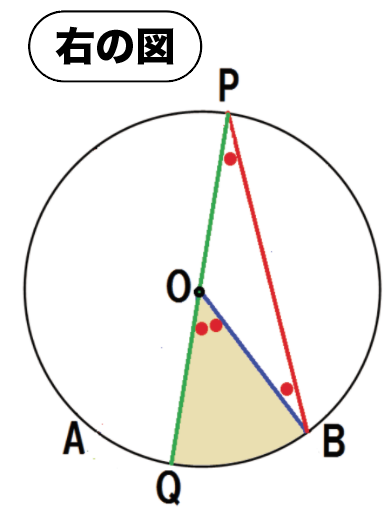
OP・OBはそれぞれ円Oの半径だから、OP = OB
よって、△OPBはOP = OBの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OBP = ∠OPB ・・・ (4)
三角形の外角の定理より、
∠BOQ = ∠OBP + ∠OPB・・・(5)
(4)、(5)より、
∠BPQ = 1/2∠BOQ・・・(6)
で,右半分の図と左半分の図を元通りに重ね合わせると,
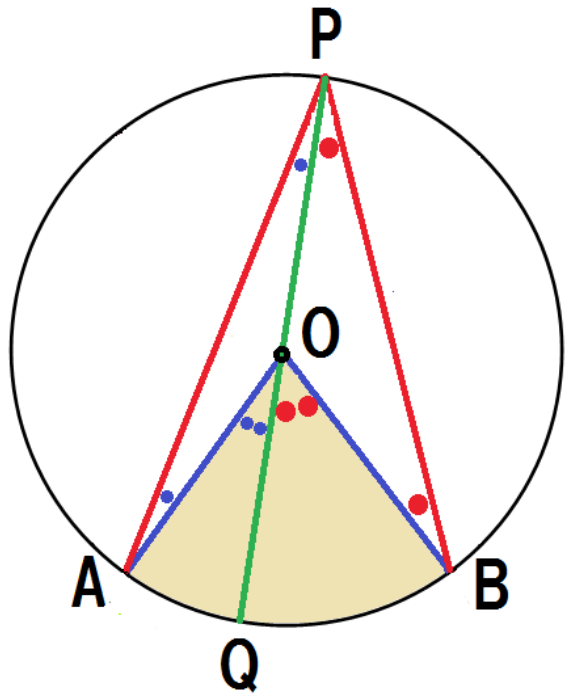
(3)+(6)より、
∠APQ +∠BPQ= 1/2∠AOQ + 1/2∠BOQ
よって、
∠APB = 1/2∠ AOB
よって、
円周角∠APBは中心角∠AOBの半分である。
最後は、
中心Oが∠APBの外にあるパターンね。
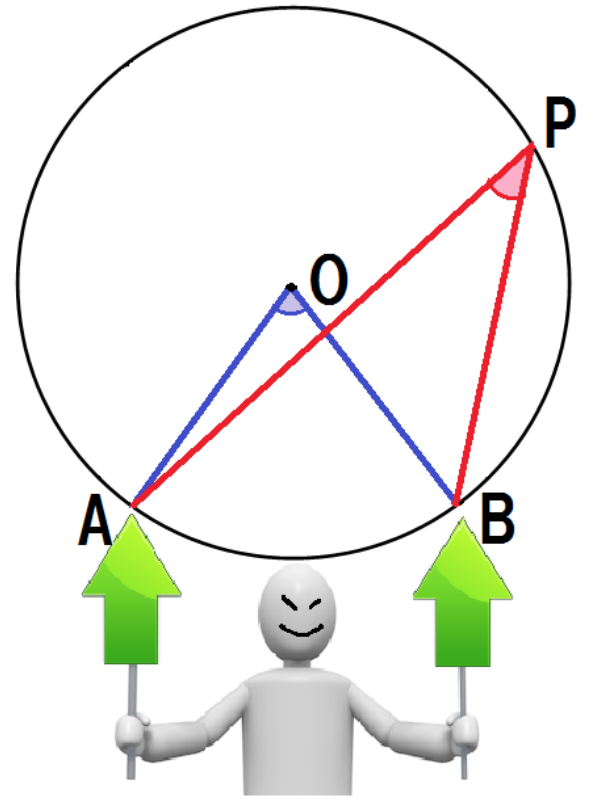
またまた補助線引くよ。
OPを延長した線分と円周の交点をQとするぞ。
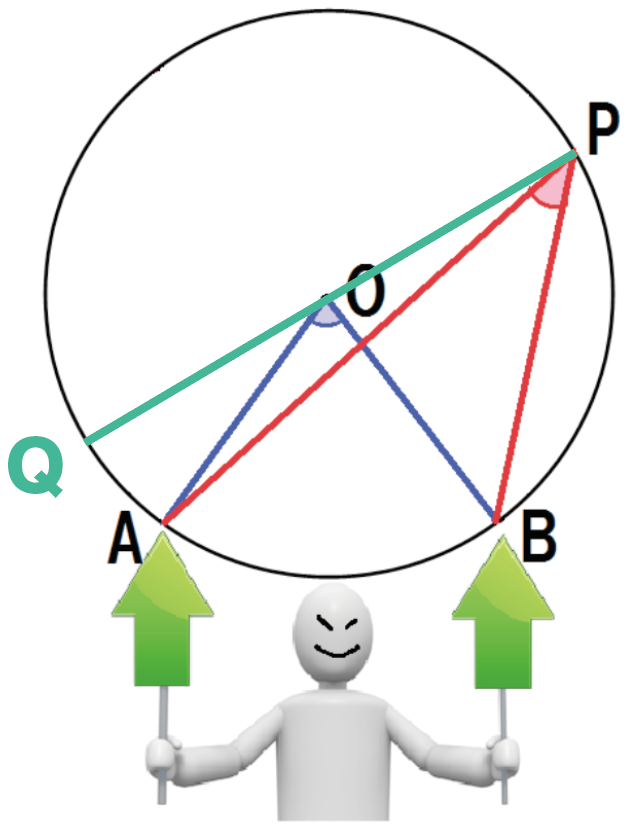
ややこしいから、目を皿のようにして見とけよ!

同じように図形を分解して、見やすくしてみるね。
重なりをバラバラにして、
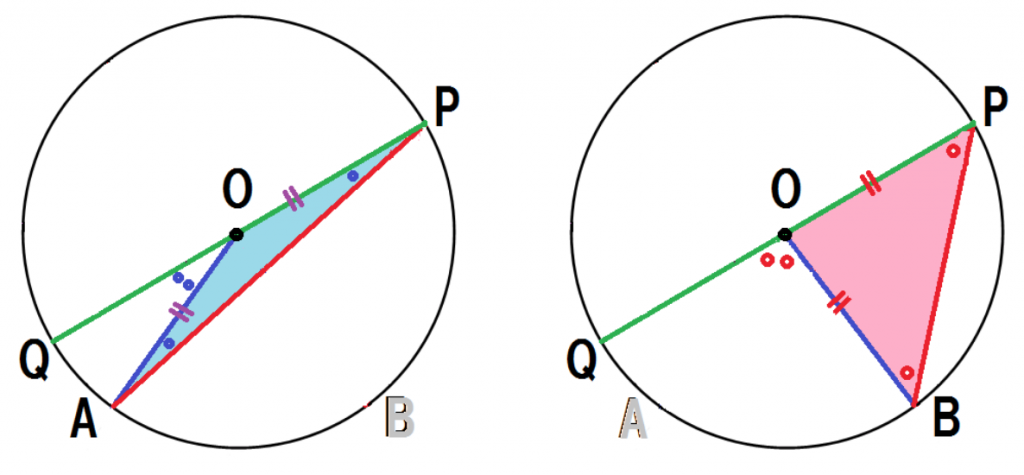
左と右でそれぞれ分けて考えてみるよ。
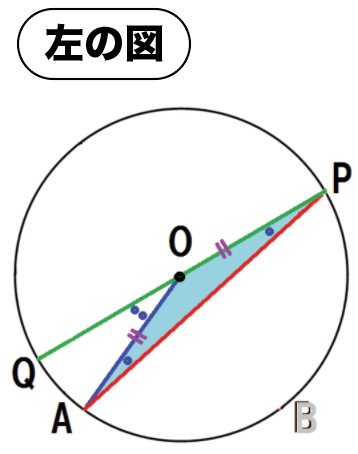
OP・OAはそれぞれ円Oの半径だから、
OP = OA
よって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)
三角形の外角の定理より、
∠AOQ = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APQ = 1/2∠AOQ・・・(3)

OP・OBはそれぞれ円Oの半径だから、
OP = OB
よって、△OPBはOP = OBの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OBP = ∠OPB ・・・ (4)
三角形の外角の定理より、
∠BOQ = ∠OBP + ∠OPB・・・(5)
(4)、(5)より、
∠BPQ = 1/2∠BOQ・・・(6)
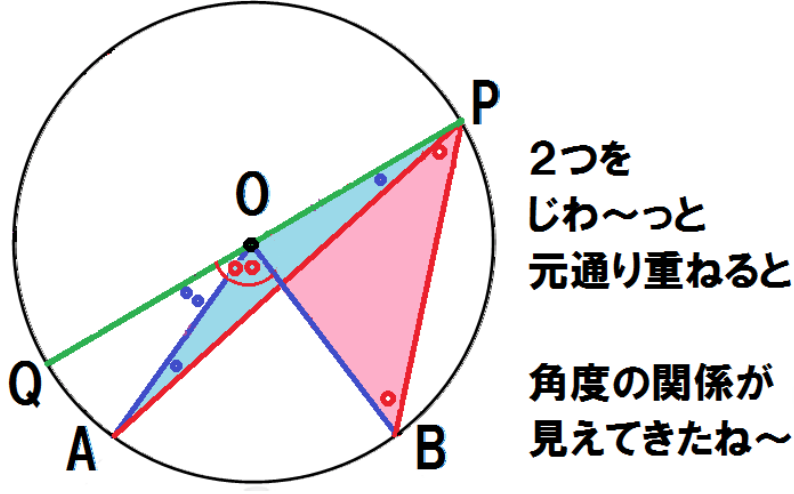
(3)・(6)より、
∠BPQ -∠APQ = 1/2∠BOQ – 1/2∠AOQ
よって、
∠APB = 1/2∠AOB
よって、
円周角∠APB は∠AOBの半分である。
円周角の定理の証明はどうだったかな??
つぎの3パターンの証明ができればよかったよね?
3パターンとも証明しちゃったんだから使いホーダイ。

円周角の定理を心気なくガシガシ使っていこう。
じゃあな。
Dr.リード
どーもー!ぺーたーだよ。
今日は、
「円」と「三平方の定理」を合体させた問題の説明をするよ。
その一つの例として、
円の弦の長さを求める問題
が出てくることがあるんだ。
たとえば、次のような問題だね。
練習問題
半径6cmの円Oで、中心Oからの距離が4cmである弦ABの長さを求めなさい。

弦っていうのは、弧の両端を結んでできる直線だったね。
ここでは直線ABが弦だよ。
この「弦の長さ」を求めてねっていう問題。
この問題を今日は一緒に解いてみよう。
自分のペースでついてきてね!
弦の長さを求める問題は次の3ステップで解けちゃうよ。
練習問題
半径6cmの円Oで、中心Oからの距離が4cmである弦ABの長さを求めなさい。

まずは、
「弦の端っこ」と「円の中心」を結んで、
直角三角形を作っちゃおう。
練習問題では、
AからOへ、BからOへ線を書き足したよ。

弦ABとOの交点をHとすると、
△AOHは直角三角形になるよね?

これで計算できるようになるんだ。
次は、直角三角形で「三平方の定理」を使ってみよう。
練習問題でいうと、
△AOHは直角三角形だから三平方の定理が使えそうだね。

三平方の定理を使って残りの「AHの長さ」を出してみようか。
こいつに三平方の定理に当てはめると、
4²+x²=6²だから
16+x²=36
x²=3²-16
x²=20
x>0より
x=2√5
になるね。

だから、AH=2√5㎝になるってわけ。
あとは弦の長さを求めるだけだね。
弦の性質を使ってやればいいのさ。
弦の性質についておさらいしておこう。
円の中心から弦に垂線をひくと、弦との交点は弦の中点になる
って性質だったね。
「えっ、そんなの聞いたことないんだけど」
って人もいるかもしれないけど、意地でも思い出してほしいね。
∠AHO=90°ってことは、OHは垂線ってことだね。
だから、弦の性質を使うと、
Hは弦ABの中点なんだ!

ABの長さはAHの2倍ってことだから、
AB = 2AH
=2√5×2=4√5
つまり、
弦ABの長さは 4√5 [cm] になるんだね。

おめでとう!
弦の長さの問題はどうだったかな??
の3ステップでじゃんじゃん弦の長さを計算していこう。
じゃあ今日はこれでおしまい!
またね!
ぺーたー
やあ,Dr.リードだぞいっ!!
円周角の定理は頭に入ったよな!!
だよな!
円周角の定理はおぼえるだけじゃだめだ。
実際に、いろんな問題を解いてみることが大事なんだ。
円周角の問題を解くコツは、
でっかく自分で図をかいてみること。
問題集の円なんて、小さすぎて見にくいだろ??
これだと考えにくいから、
ノートや別の紙にお皿くらいでっかく描いて考えてみるといいな。
そうそう。でっかくでっかく。
中華料理のターンテーブルみたいにさ、くるくる回しやすいだろ?

今日は、テストにでやすい円周角の求め方を3パターン紹介していくぞ。
円周角の求め方は意外とシンプルでわかりすいんだ。
まずは、円周角の定理を使った求め方だね。
円周角の定理は、
の2つだったよな?
忘れたら円周角の定理の記事で復習しような。
それじゃあ円周角の問題を解いていくぞ。
次の角xを求めなさい。
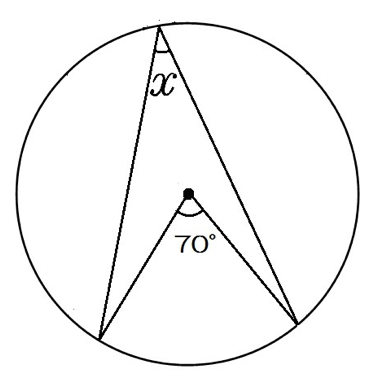
この問題では円周角の定理の、
1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である。
を使っていくぞ。
円周角は中心角の半分。
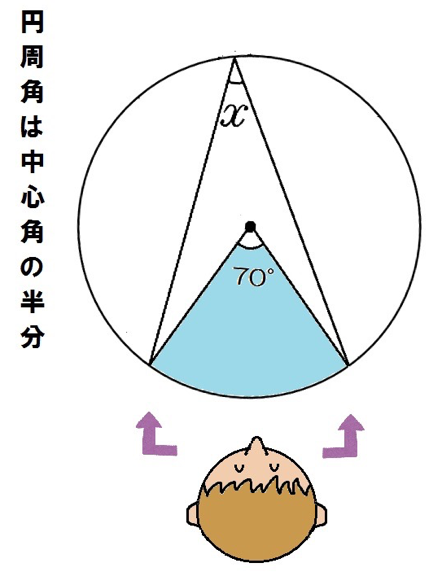
だから、xは35°だ。
次の角xを求めなさい。
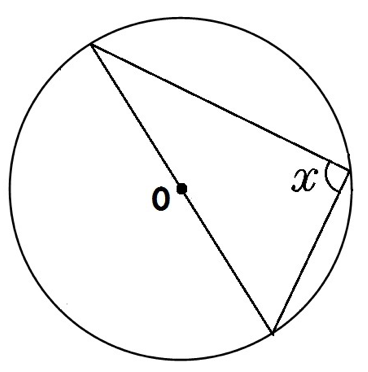
この円周角の求め方もさっきと同じ。
同じ孤に対する円周角は中心角の半分。
この円は円の半分だから、中心角は180°。
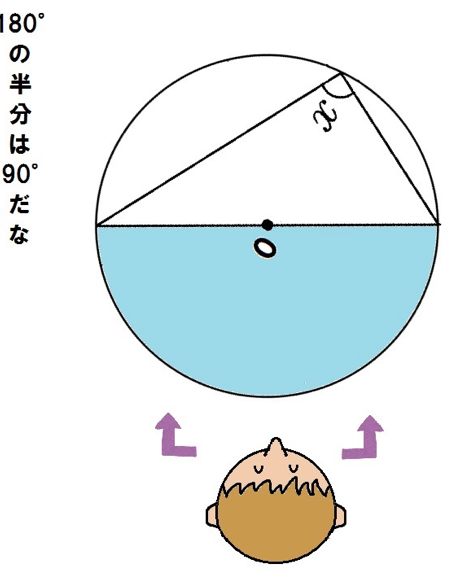
よって、円周角のxは90°。
これも基本通り。
直径に対する円周角は90° はよくでてくるぞ。
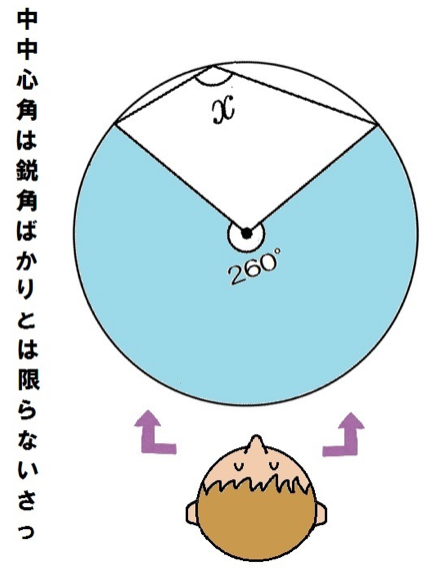
次の角xを求めなさい。
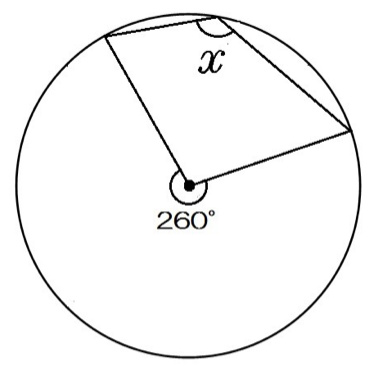
この問題も同じさ。
中心角が260度だから、円周角xはその半分で
130度。
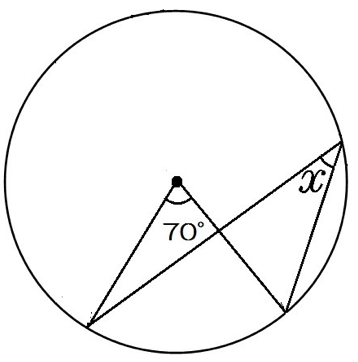
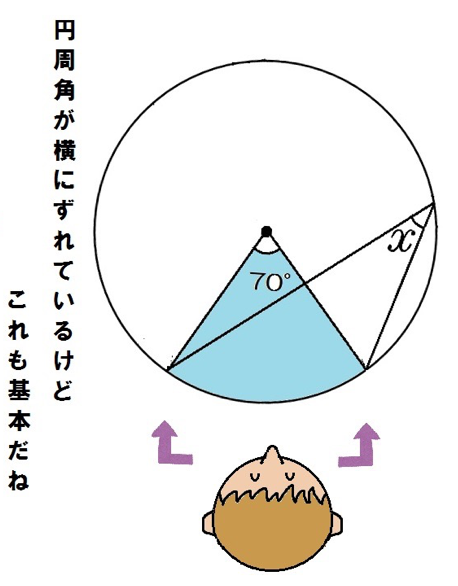
円周角の頂点が中心角からずれてるパターン。
基本の求め方は同じだぞ。
円周角は中心角70°の半分だから35°だ。
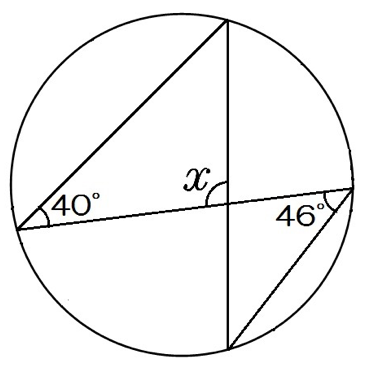
リボンタイプの問題っておぼえておくといいよ。
中心角はかかれてない。
この問題では、
同じ弧の円周角はどこも同じってことを利用する。
角xは、
180-40-46=94°
になるね。
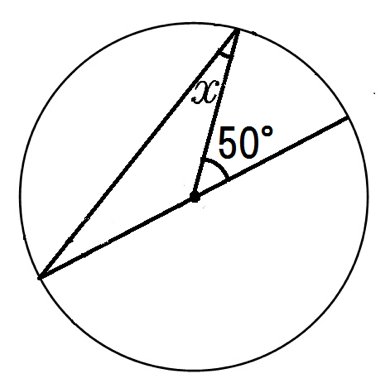
げっ、円周角じゃないとこきかれてるじゃん。
でも中心角を頂角にする三角形が「二等辺三角形」ってことを利用すると・・・
つまり50°の半分、25°が円周角だね。
二等辺三角形の底角は等しいからxも25°。
次はちょっと難しい問題。
補助線を引かないと円周角が求められないやつだ。
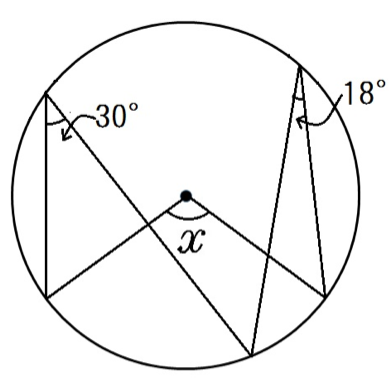
さあ、補助線を引くぞ。
中心角を2つに分けられる補助線を引けばいいんだ。
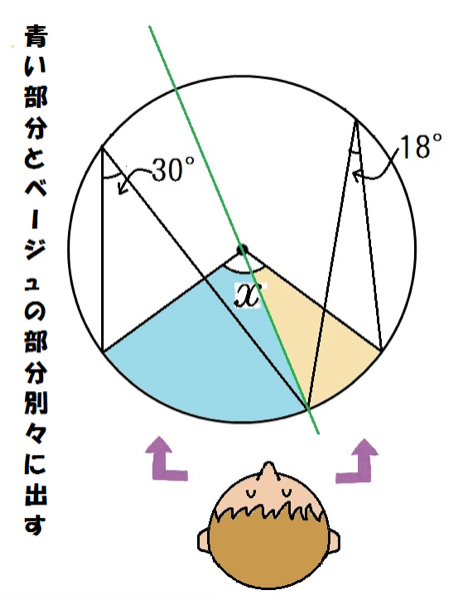
補助線さえ引けたら,円周角の問題が2つドッキングしてるだけなんだよね。
青いほうが円周角の2倍だから60°。
ベージュのほうが円周角の2倍で36°。
合計でxは96°だ。
補助線引けないと手も足も出ないが、コツさえつかめばだいじょうぶ。
最後は、中心角・円周角出したその先がある問題。
もうひと踏ん張りのパターンだ。
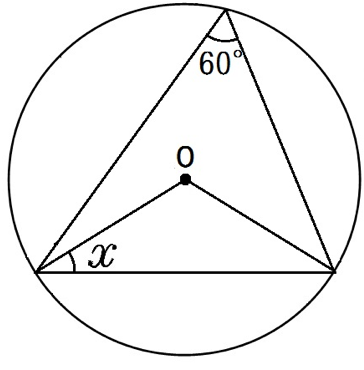
円周角60°ってことは、中心角は2倍の120°。
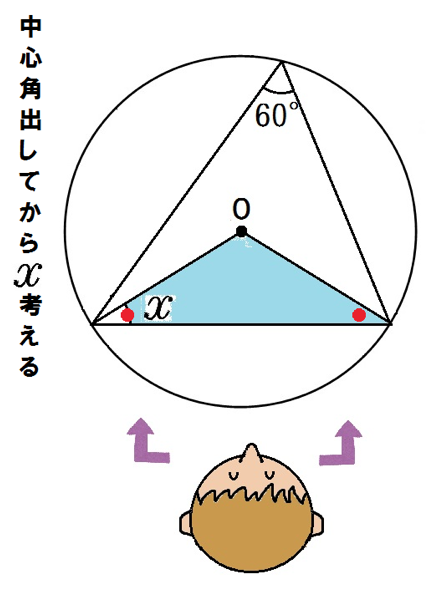
水色の三角形は二等辺三角形だから底角は等しい。
よって、底角のxは、
(180-120)÷2=30
になるぞ。
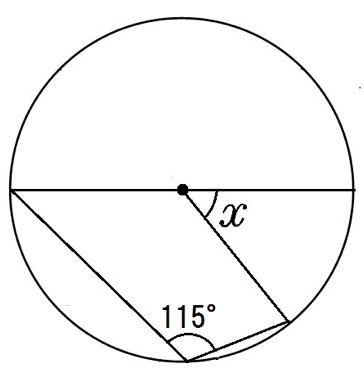
円周角115°だから、赤い中心角は2倍の230°。
紫のとこは、
360-230=130°
だから、求めるxは、
180-130=50°
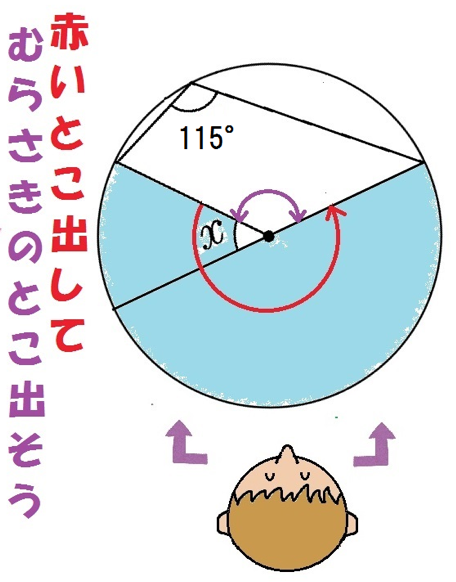
うんうん。
みるからに50°だ。
円周角の求め方はパズルみたいだね。
変に難しく考えなくて大丈夫。
あとは円の見方を変えたりするぐらいかな。
テストによく出てくるから復習しておこうぜ。
じゃ、おつかれさん。
一緒に中華料理でも食うかな!
Dr.リード

こんにちは!ぺーたーだよ。
中3数学の「円の性質」では、
を勉強してきたね。
今日はこいつらを使って、
円周角で角度を求める問題
にチャンレジしていこう。
円周角の定理をむちゃくちゃ使うから、
「まだよくわかんない…」っていう人は、
円周角の定理を復習してみてね。
さっそく、円周角で角度を求める問題をといていこう。
テストで役立つ3つの問題をいっしょにといてみよう。
つぎの円Oにおいて角度xを求めなさい。
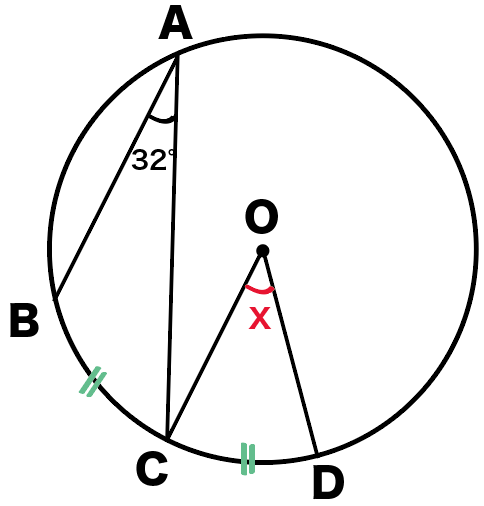
ただし、
孤BC = 孤CDとします。
この問題では、円周角の性質の、
1つの円で等しい弧に対する円周角の大きさは等しい
をつかっていくよ。
孤BC = 孤CDだから、
孤BCと孤CDがつくる円周角は等しいはずだね。
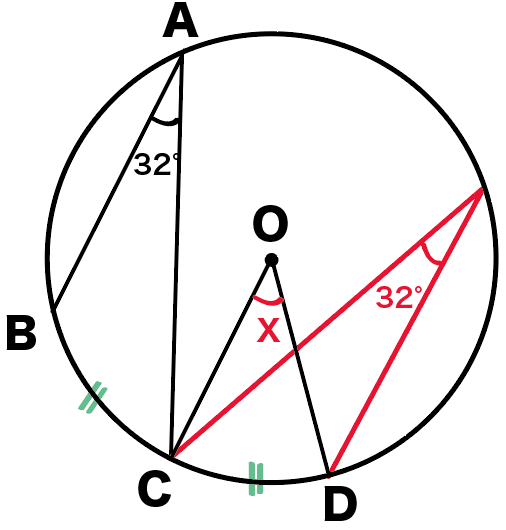
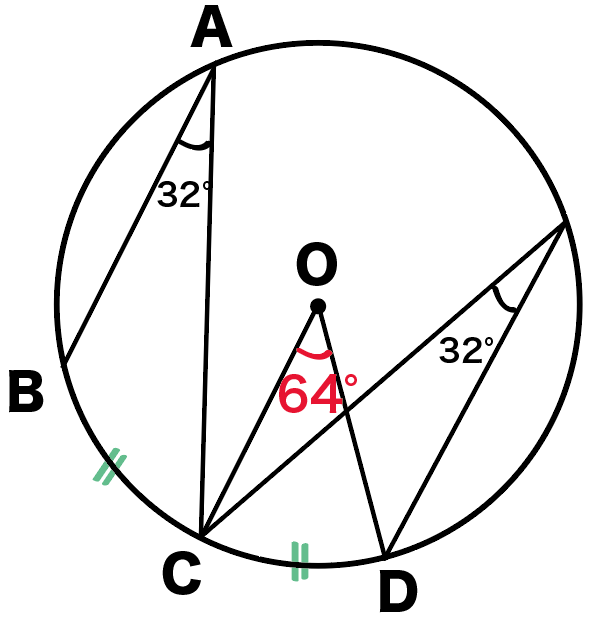
ってことは答えはもう簡単!
弧BCの円周角BACが32°だから、
弧CDの円周角も32°ってことだね!
でも、問題で求めたい角xは、
孤CDの円周角じゃなくて中心角だ。
円周角の定理より、
同じ孤の円周角を2倍すると中心角になるんだったね??
ってことは、角xは円周角32°を2倍した、
∠x = 64°
になるはず。
つぎの円Oにおいて角xを求めなさい。
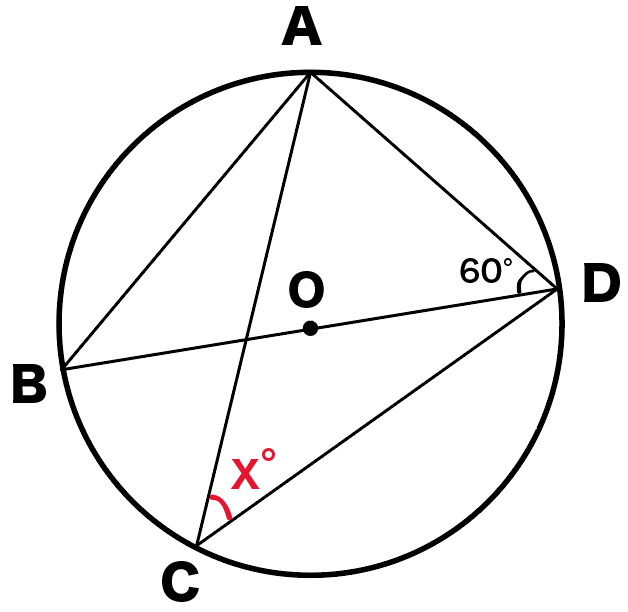
この問題では、
をフルフルにつかっていくよ。
まず、円周角の性質の、
半円の孤に対する円周角は90°
ってやつをつかってみよう。
円周角BADは半円に対する円周角だから、
∠BAD = 90°
になるね。
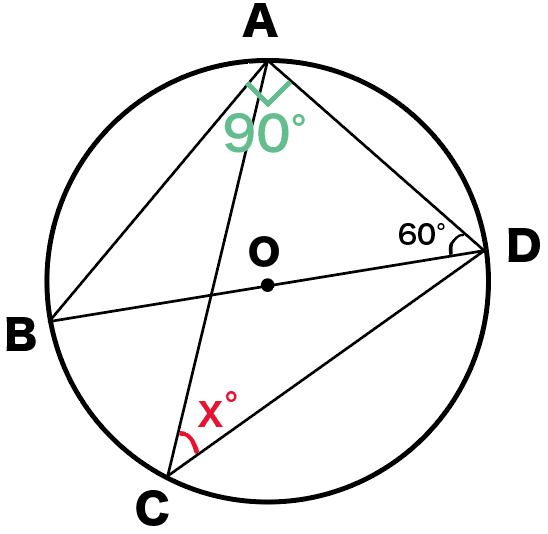
んで、ここで△ABDに注目してみよう。
三角形の内角の和は180°だったよね??
△ABDの内角のうちの2つの、
がわかってるよね??
ってことは、残りの内角の∠ABDは、
∠ABD
= (三角形の内角の和)- (∠BAD + ∠ADB )
= 180 – (90+60)
= 30°
になるね!
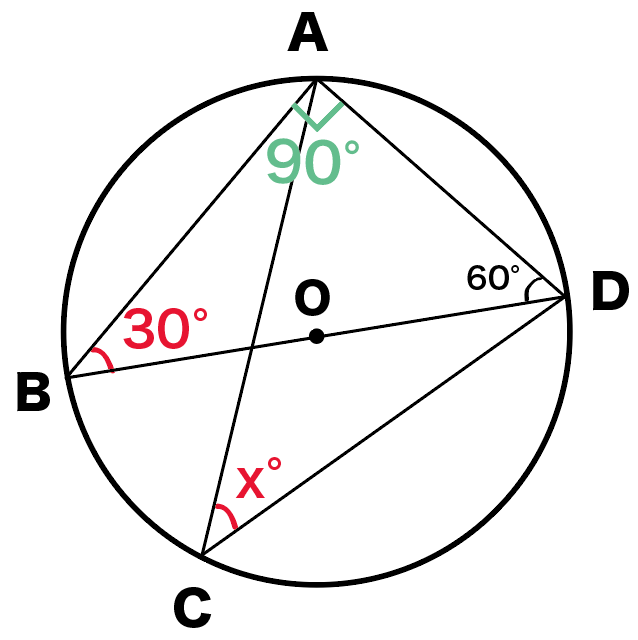
つぎは、円周角の定理をつかうね。
同じ弧に対する円周角は等しい
っていう定理をつかうと、
∠ABD = ∠ACD = 30°
になるね。
なぜなら、
両方とも孤ADに対する円周角だからね。
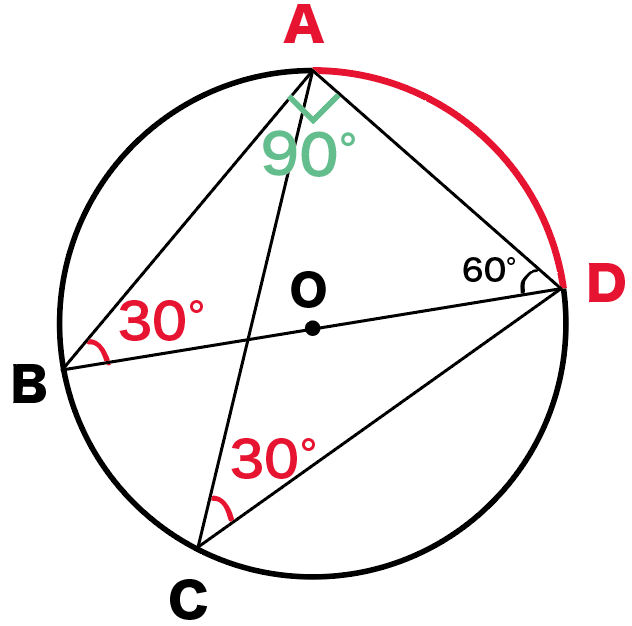
ってことで、
xは30°ね!
つぎの円Oにおいて∠xを求めなさい。
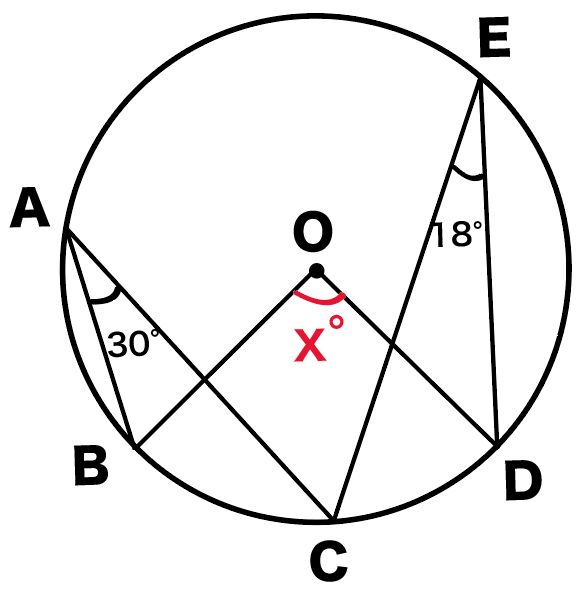
次はちょっと手ごわそうだねー。
こいつはこのままだと答えまで出すのは
難しいかもしれないね。
だから、自分で線を1本足してあげよう。
どこに付け足すかわかるかな?
そう。そうだよ。
AとDをむすんでみて!
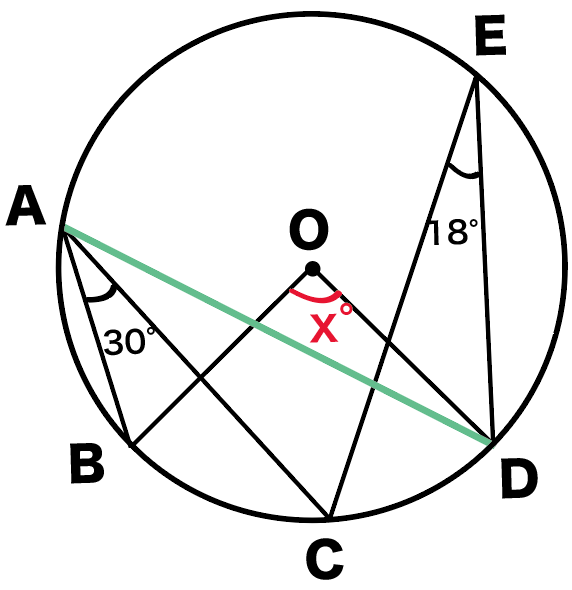
この1本の補助線が答えまで案内してくれるよ!
同じ弧の円周角は等しいんだったよね?
ってことは、
∠CED = ∠CAD = 18°
になるね。
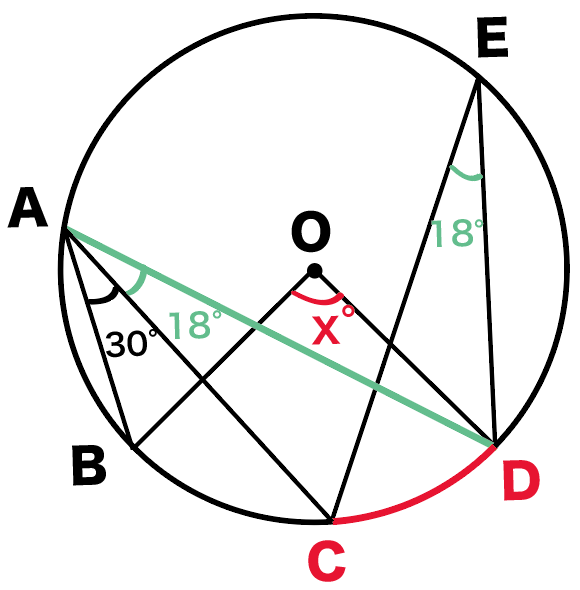
そうすると今度は、
∠BAD = 48°
になるね。
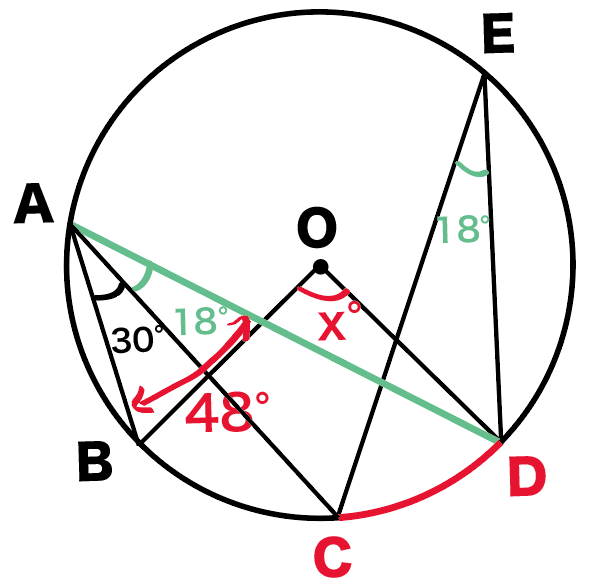
∠BADは求めたい∠BODの円周角。
ってことは、
円周角の定理の、
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分
ってやつをつかえばいいね。
すると、
x= ∠BAD×2
= 48°×2 = 96°
になるね!
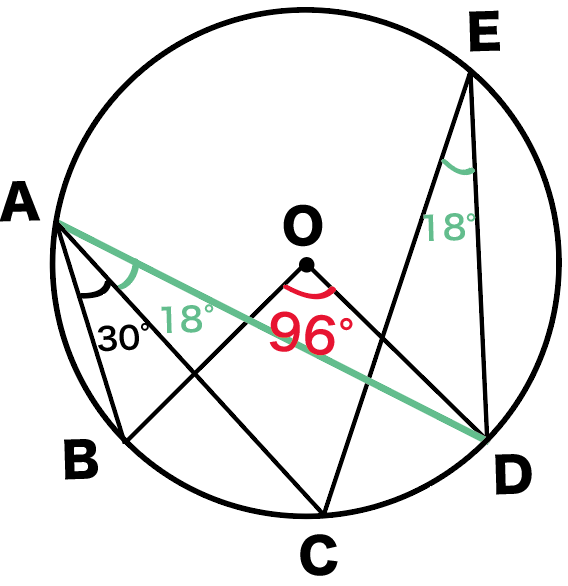
円周角の角度の問題はどうだった??
最初は慣れないかもしれないけど、
とけると面白いはず。
円周角を求める問題が出てきたら、
解いてみるといいね!
じゃあ、今日はここまで!
ぺーたー
こんにちは!ぺーたーだよ。
この前は、円周角の定理とはなにか??
ってことを勉強してきたよね。
今日はもう一歩ふみこんで、
円周角の性質
をまなんでいこう。
中学数学で勉強する円周角の性質は、
ぜんぶで3つ。
3つ覚えておけばいろんなとこで活躍するよ。
「できれば覚えておいてほしい」というよりは、
「絶対言えるようになってね!」っていう内容だね。
どんな性質なのか見ていこう!
中学数学で役に立つ「円周角の性質」はつぎの3つだよ。
それぞれ順番にみていこうか。
これは円周角の定理の復習。
円周角の定理に、
同じ弧を共有してる円周角はどれも等しい
っていうやつがあったよね。
これはね、円周角の問題を解く時によくでてくるから、
絶対におさえておきたい性質だね。
たとえば、つぎの円Oがいたとしよう
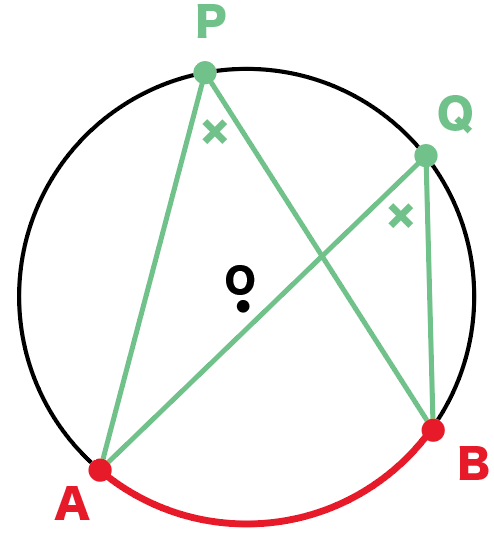
このとき、
角APBと角AQBは、
弧ABの円周角だよね??
さっきでてきた円周角の定理をつかうと、
角APB = 角AQB
ってことがいえるんだ。
たとえば、角APBが50°だとすると、
角AQBもおなじ50°になるわけ。
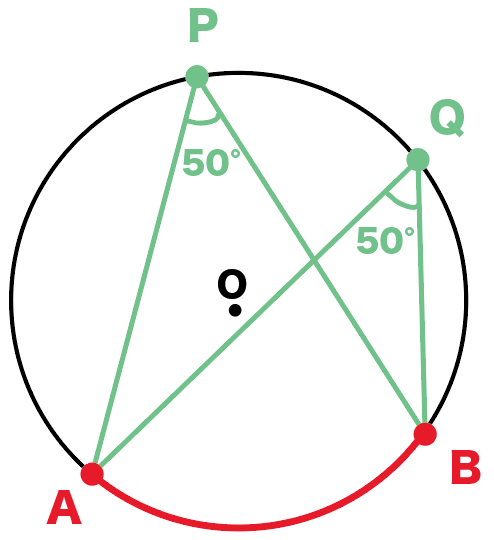
これは円周角の問題では絶対に知っておきたい性質だね。
2つ目の円周角の性質は、
等しい弧の円周角は等しいよ
ってやつね。
円周角の問題でむちゃくちゃよく使うよ。
たとえば、つぎの下の円をイメージしてみて。
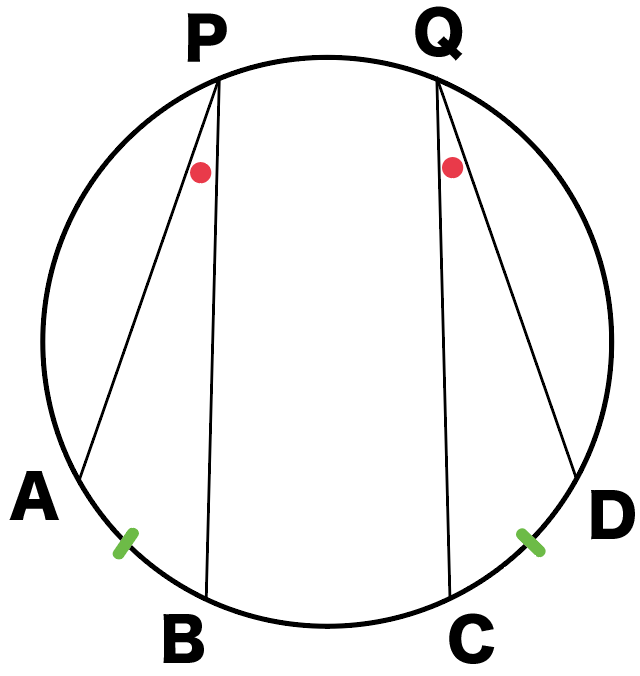
円周上に弧ABと弧CDがあるよね。
それぞれ円周角∠APB、∠CQDがあるけど、
2つの弧の長さが等しいとき(弧AB=CD弧)、
円周角も同じ大きさになるっていう性質だよ。
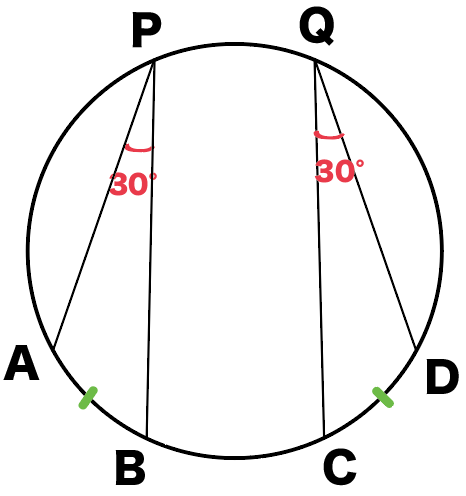
つまり、
∠APB=∠CQD
がいえるんだ。
だから、
∠APB=30°だとしたら、
∠CQDも30°になるってわけ。
この円周角の円周角の性質はちらっとでてくることがあるよ。
よく復習しておこう。
いよいよ最後の円周角の性質。
もし、弧が半円のやつだったら、そいつの円周角は、
90°になる
っていう性質だね。
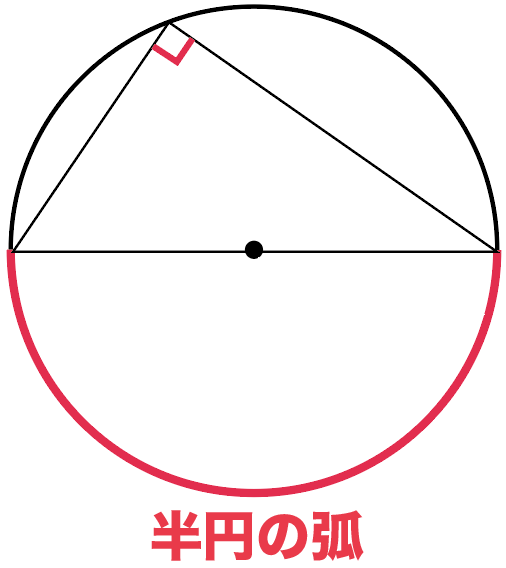
「えっ、そうなの!?」
ってびっくりする人もいるかもしれない。
これも、知っているのと知らないのとでは
問題を考えるときに大きな違いが出てくるから
ぜひ覚えておきたいところだね!
図で表すとこんな感じだ。
たとえば、下の円Oを想像してみて。
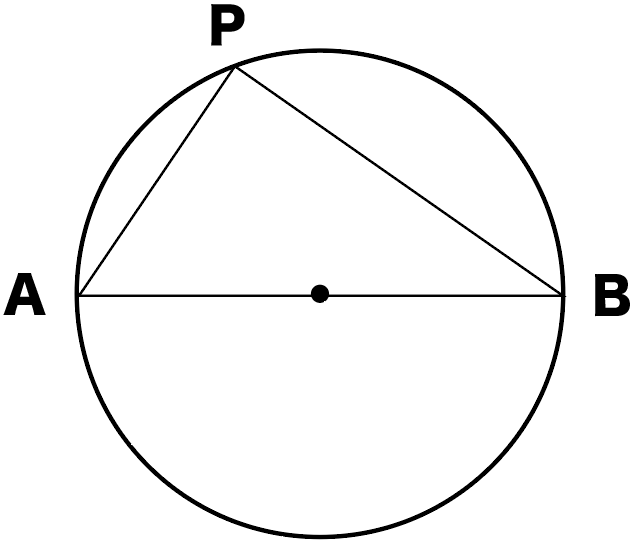
直線ABは中心Oを通ってるから、
円の直径になってるよね。
直径ABで円を切ると半円になるから、
弧ABは半円の弧になってることがわかる。
よって、
半円の弧に対する円周角の角APBは90°になってるわけ。
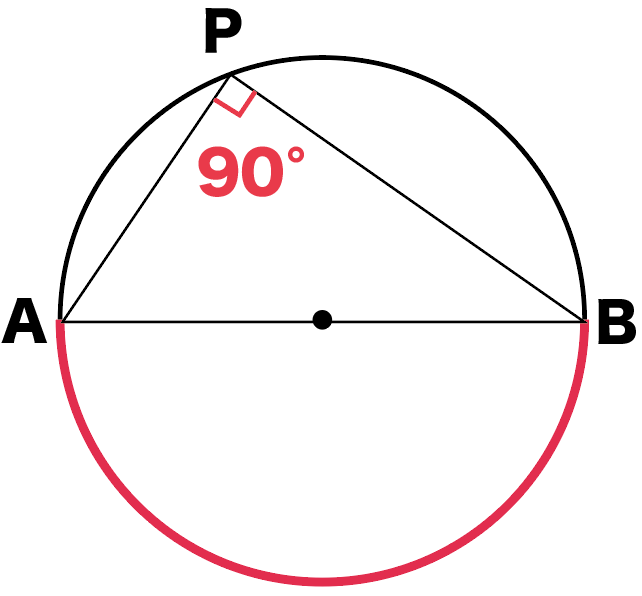
えっ。なんで半円の弧に対する円周角が90°になるのかって??
って人のために、
なぜ、半円の孤に対する円周角は90°になるのか
を説明しておこう。
って言っても、これ自体はめちゃ簡単。
円周角の定理をつかえば説明できちゃうんだ。
半円の弧に対する中心角
に注目してみて。
さっきの弧ABに対する中心角をみてみると、
直線ABがつくる180°
であることがわかるね。
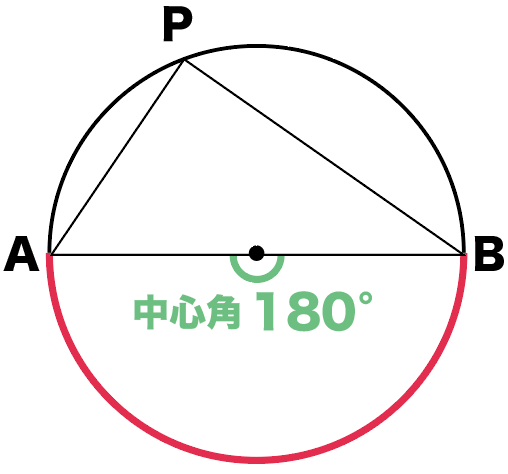
で、あとは円周角と中心角の関係を思い出そう。
1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である
だったから、
中心角の半分の大きさが円周角になるんだ!
で、中心角の∠AOBって180°だよね?
その半分が円周角なんだから、
円周角の∠APB=90°になるんだ!
これで説明終わりだよ。
意外と簡単だったでしょ?(。)
円周角の性質はどうだったかな??
ここで出てきた性質は問題を解く上では必須。
絶対忘れないようにしてね!
この円周角の性質と同じぐらい大事なのは、
だね。こっちも忘れかけてたら復習してみてね。
じゃあ、今日はこのへんで。
またね!
ぺーたー
やあ、ぺーたーだよ。
中3数学もいよいよ大詰め。
いよいよ、
円の性質っていう単元
を勉強していくよ。
今日は、この単元でいちばん大事な、
円周角の定理とはなにか??
をまとめてみたんだ。
計算や証明で使ったりするから、しっかりおさえてあげてね。
= もくじ =
円周角の定理を理解するためにはまず、
の2つの意味を知らないとね。
まず円周角からだ。
円周角とはなんだろう??
Wikipediaをみてみると、
ユークリッド幾何学においてある円周上の一点から、この点を含まない円周上の異なる二点へそれぞれ線分を引くとき、その二つの線分のなす角のことである。
ってかいてある。
これはちょっとむずかしいw
正直、ユークリッドとかわけわからんよね。
円周角をもうちょっと簡単にいってあげると、
「円周上の1点」と、
そいつと被らない円周上の2つの点を、
線分でむすんだときに、
できる角度のことを、
円周角(えんしゅうかく)
とよんでいるんだ。
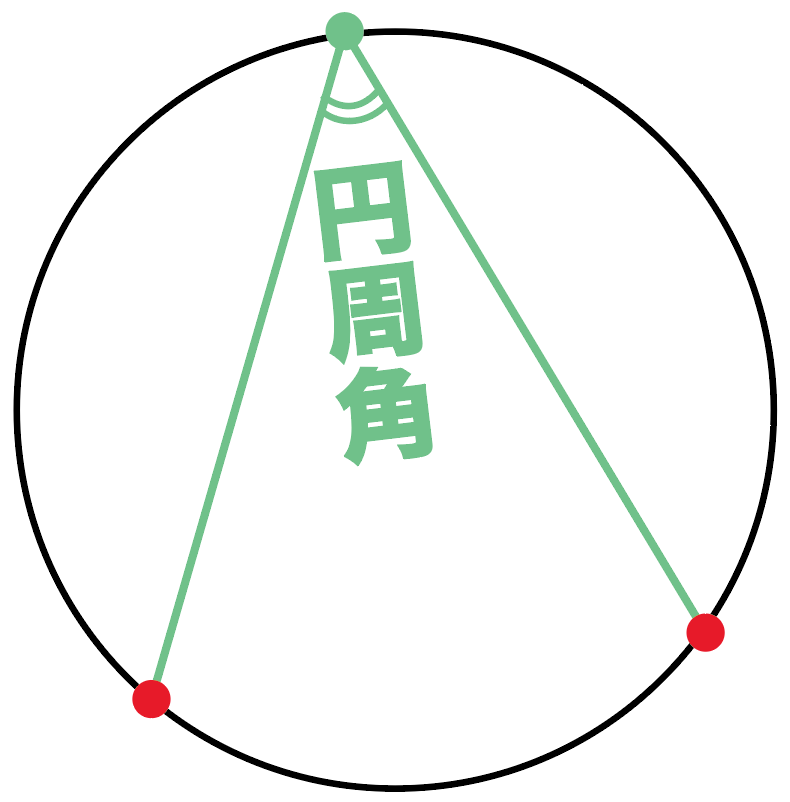
たとえば、つぎの円Oがあったとしよう。
円周上の点をA・B・Pとするよ。
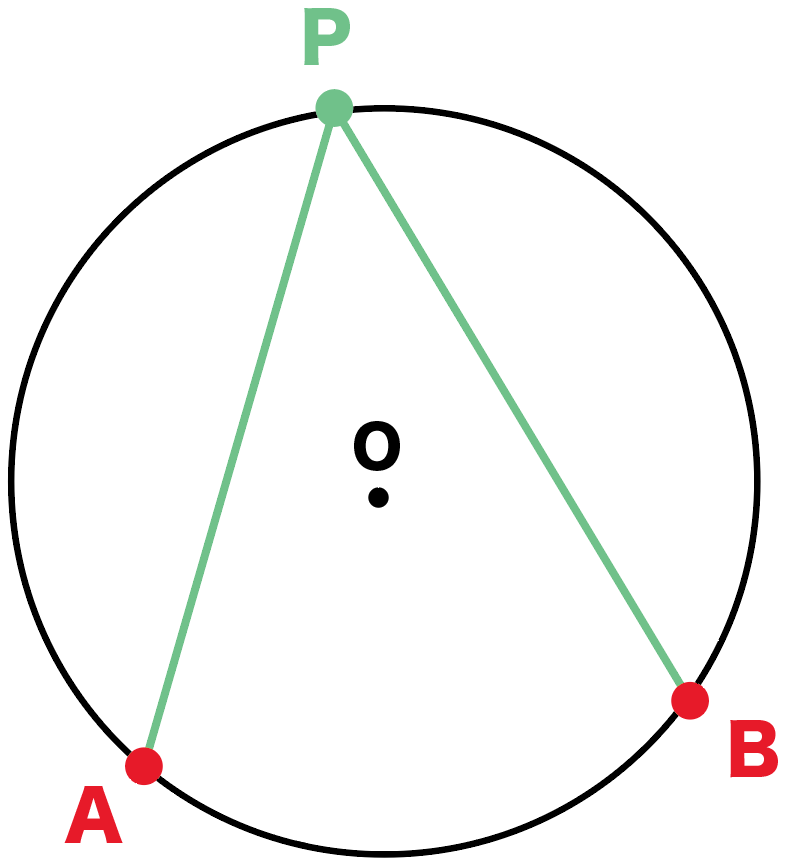
このとき、
∠APBを弧ABに対する円周角
っていうんだ。
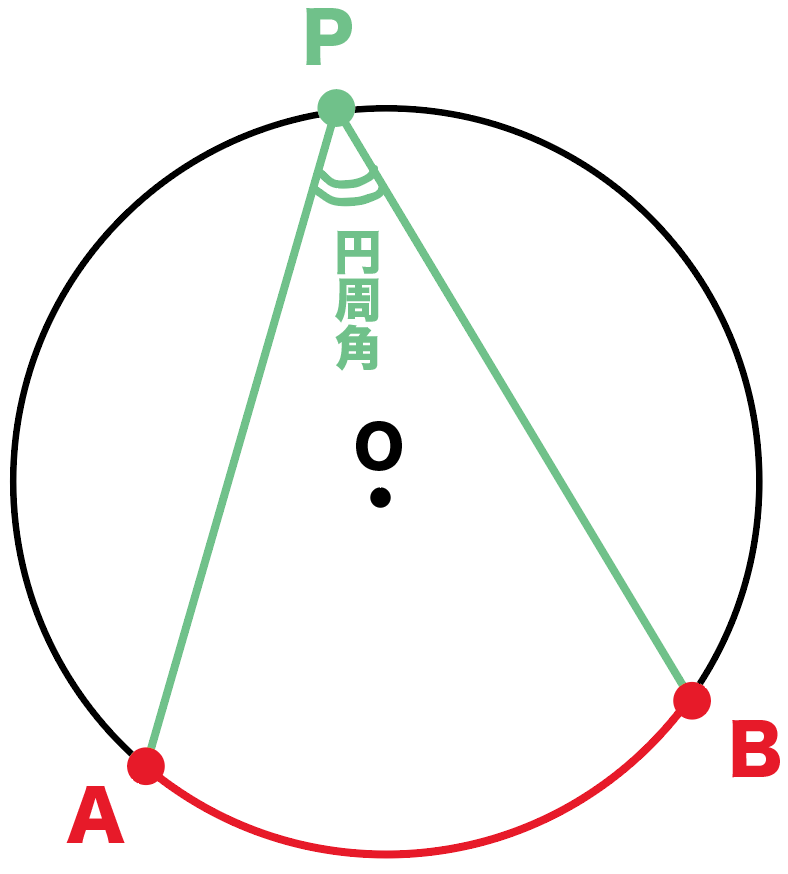
こんなかんじで、円周角には、
弧○○の円周角
というかんじで、どこかの弧に属してるってわけ。
つぎは中心角。
中心角を数学用語集でしらべてみると、
弧の両端を通る2つの半径の作る角
らしいね。
これはわかりやすい。
「円の弧」の、
「両端を通る2つの半径」が、
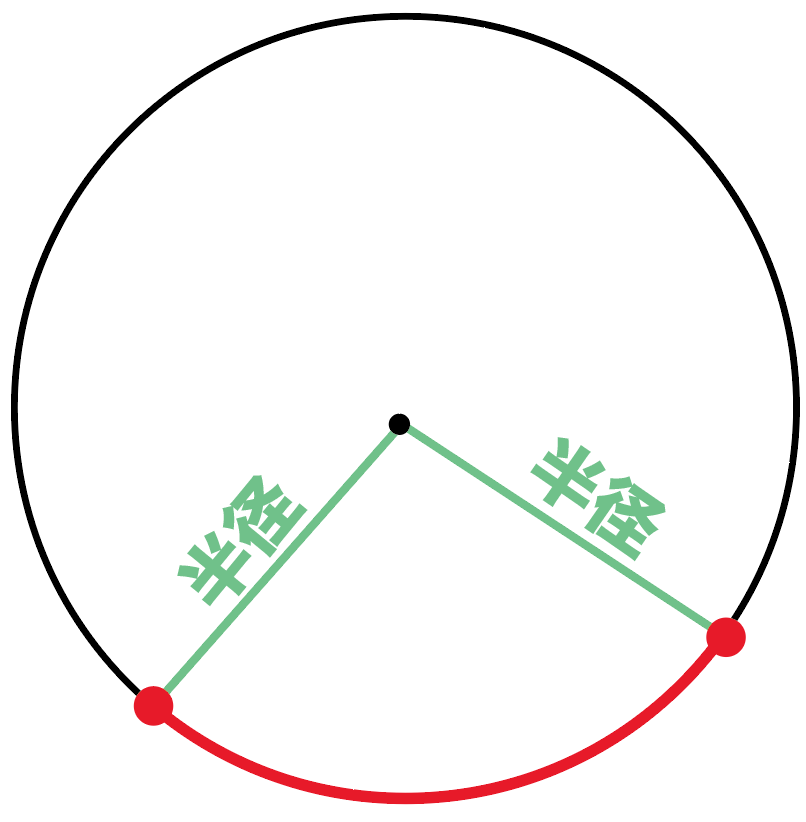
つくる角を、
中心角(ちゅうしんかく)
というんだ。
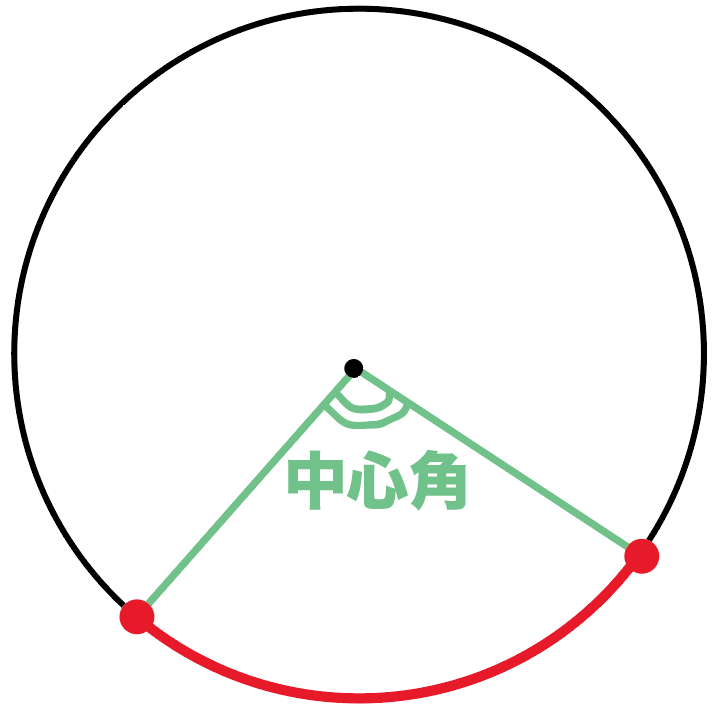
たとえば、下の円Oだったら、
∠AOBが弧ABに対する「中心角」
ってわけね。
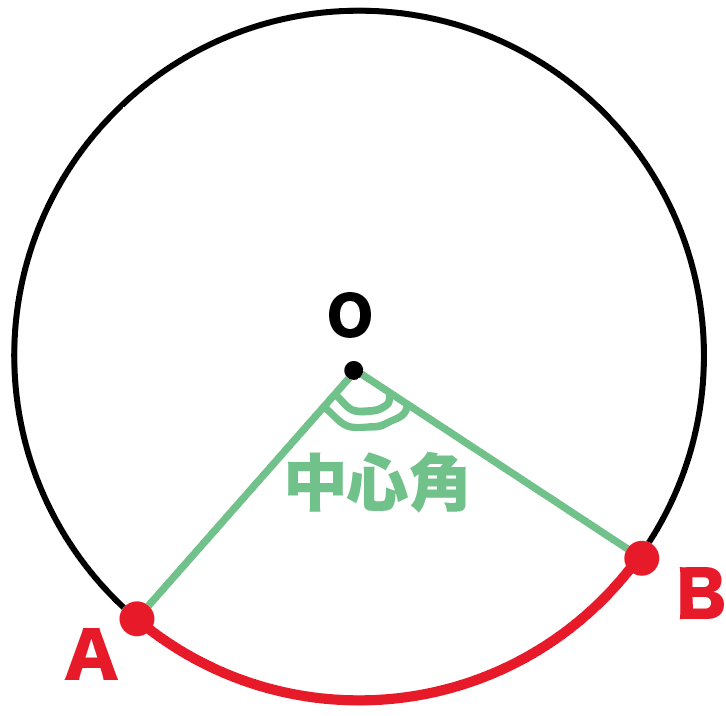
中心角も円周角とおなじように、
弧○○っていうかんじでどこかの弧に属しているよ。
円周角と中心角の違いはOKかな?
この2つの違いはしっかり理解しておいてね!
円周角の定理は、
円周角の決まりみたいなもんだ。
大切だからきっちり覚えてね!
円周角の定理は2つの性質があるよ。
つまり、
の2つの円周角の定理があるんだ。

どっちも、
「同じ弧に対する」
っていう条件が含まれてることに注意ね。
まずは、円周角と中心角の性質からだね。
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分である
っていう定理なんだ。
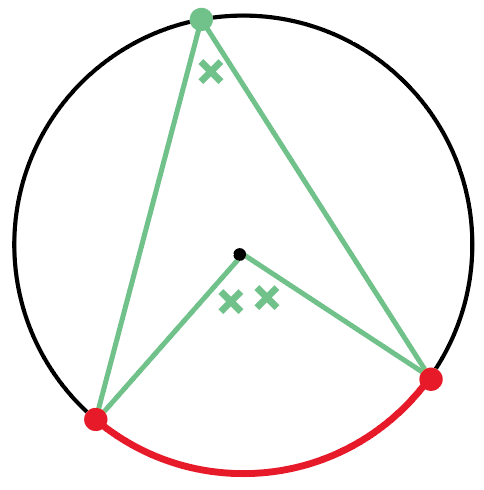
たとえば、つぎのような円Oがあったとしよう。
このとき、円周角APBは中心角AOBの半分になるんだ。
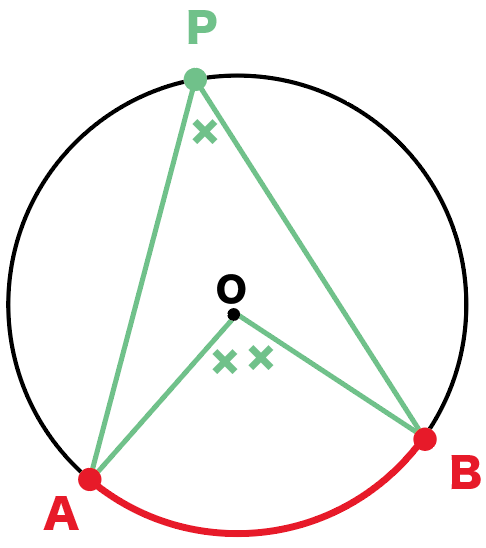
式であらわしてやると、
角APB = ½ 角AOB
になるね。
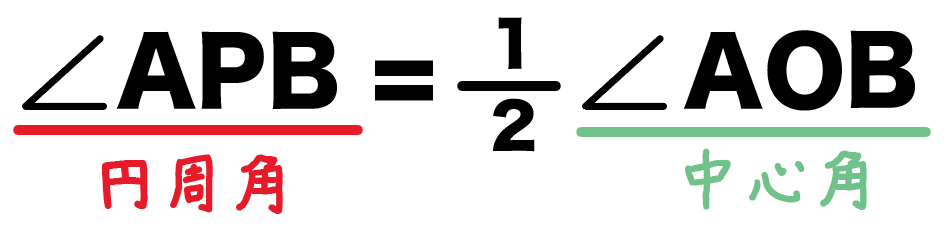
これが、円周角の定理のうち、
同じ弧に対する円周角と中心角の関係ってやつね。
だから、もし、円周角APBが「50°」だとしたら、
中心角AOBは「100°」になるってわけだね。
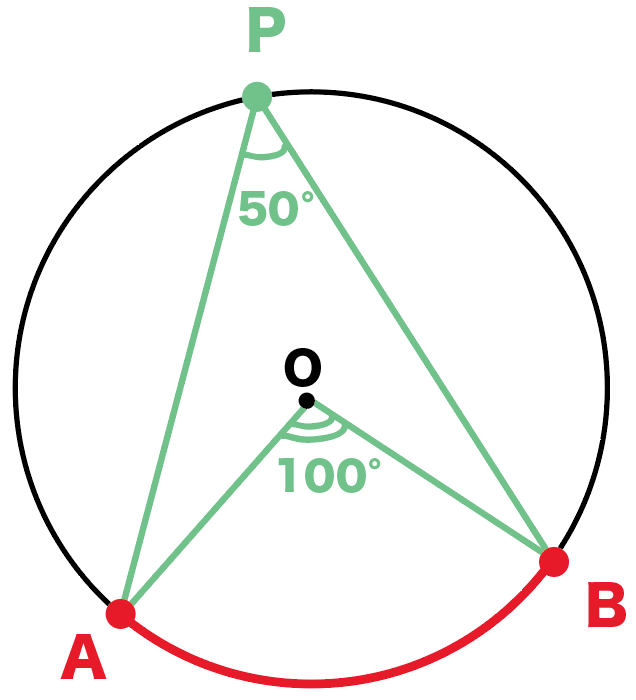
つぎは、円周角の性質だね。
なんと、同じ弧の円周角ならすべて等しいんだ。
この定理でも、
“同じ弧に対する”
っていう点に注意してね。
たとえば、下の円Oをみてみて。

もし、弧ABに対する円周角APBが「50°」だとしたら、
∠AQB = 50°
になるはずなんだ。

なぜなら、
両方とも弧 ABの円周角だからね。
円周角の定理がどんなものかわかったかな?
最後に円周角の定理を使った例題を解いてみよう。
次の図の∠xの大きさを求めてみて。
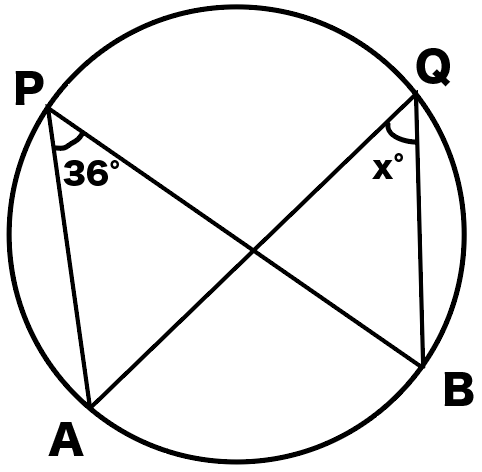
こいつはそんなに難しくないかもね!
1つの弧に対する円周角の大きさは等しいから、
∠APB = ∠AQB
になるんだ。
だから∠x=36°だね!
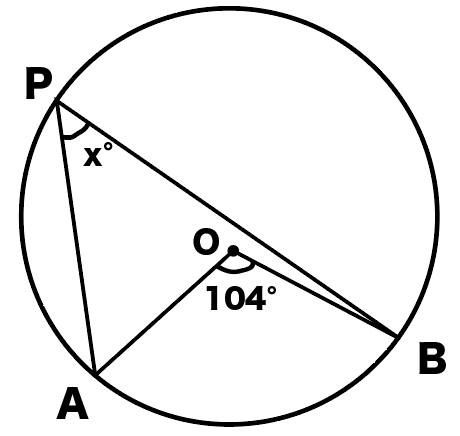
この問題は解けそうかな?
弧ABの円周角がx、∠AOBが弧ABの中心角
っていうことを見抜けると答えが出るよ。
そうすると円周角の定理の、
1つの弧に対する円周角の大きさは
その弧に対する中心角の半分である
をあてはめてやって、
∠x=104÷2
=52
ってことで、
答えは52°だね!
どうだったかな?
円周角の定理がどんなものか
理解できたかな?
どこが円周角で、どこが中心角なのか
ぱっぱと頭の中で分かるようになるのがカギだね。
円周角の定理を使った問題をくりかえしやってみてね。
最初にも言ったけど、証明問題でも活躍するから覚えといてね!
じゃあ、お疲れ!またね!
ぺーたー