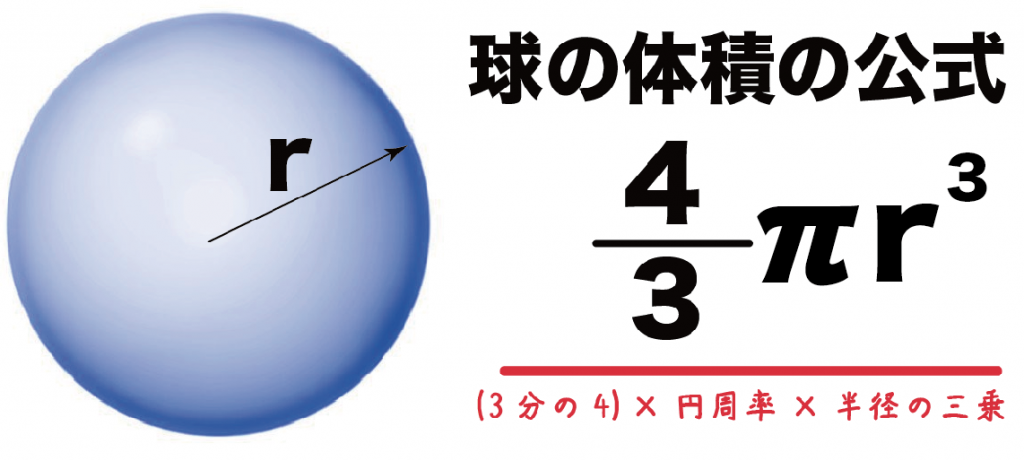
【中学数学】球の体積の求め方の公式を1発で覚える方法
球の体積の求め方の公式が覚えられねえ!!
こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。
球の体積の求め方には公式があるんだ。
球の半径をrとすると、体積の求め方は、
$$\frac{4}{3}πr^3$$
になるよ。
つまり、
3分の4 × 円周率 × 半径 × 半径 × 半径
ってことだね。
この公式でどんなボールの体積も計算できちゃうんだ。
たとえば、半径30 [cm]のサッカーボールがあったとしよう。

こいつの体積は「4/3 × π × 半径の三乗」という公式をつかってやると、
$$\frac{4}{3} × π × 30 × 30 × 30= 36000π [cm³]$$
になるね。
これってサッカーボールの中にどれぐらい空気が入っているか?ってことなんだ。
ちょっとすごくない。?
ただ、この公式にも一つだけ欠点がある。
それは、
むちゃくちゃ暗記がむずかしい
ってことさ。
3分の4なんてどっから来た数字かわからないし、半径を何回かけたらいいのかわからない。
これじゃあ球の体積の問題をだされたらやばすぎる・・・・
そこで、今日は、
中学生でもおぼえられる「球の体積の求め方」を解説していくよ。
球の体積の公式を忘れちゃったときに参考にしてみて。
球の体積の公式を1発で覚える方法
「球の体積の公式」を暗記する方法を伝授しよう。
3分の4 × 円周率 × 半径の三乗
という公式はつぎの語呂を使えばおぼえられちゃうよ。
さんしろう、おいしいパイを持ってある日参上

えっ。
あ、大事だからもう一度繰り返すよ。
さんしろう、おいしいパイを持ってある日参上
なぜこの語呂で「球の体積の公式」おぼえられるのか。
それは、
さんし(3分の4)ろう、美味しいパイ(π)を持ってある(r)日参上(三乗)
になるからさ。
つまり、
- 「さんしろう」→「$\frac{4}{3}$」
- 「おいしいパイ」→「π」
- 「ある日」→「r」
- 「参上」→「三乗」
という感じで、それぞれの言葉が対応してるってわけ。
だから、
さんしろう、美味しいパイを持ってある日参上

という語呂を覚えてしまえば「球の体積の求め方」の公式も一生忘れないってことさ。
おめでとう!!
まとめ:中学数学の「球の体積の公式」は語呂で制す
中学数学では「球の体積の公式」が使える理由がわからない。
完全に理解するためには「積分」という知識を使わなきゃいけないんだ。
だからこそ、中学生の間は、
さんしろう、美味しいパイを持ってある日参上

という語呂で「球の体積の公式(3分の4 × 円周率 × 半径の三乗)」をおぼえてしまおう。
テスト前にがんばって暗記してみてね。
そんじゃねー
Ken
なぜ球の公式がつかえるのか気になったらみてみて↓