「ねじれの位置」にある2直線をみつける3つのステップ
「ねじれの位置」とか、よくわからんわ!
こんにちは、この記事をかいているKenだよ。インスタントみそ汁は神だね。
中1数学にでてくる謎の1つに「ねじれの位置」というものがある。
えっ。ねじれの位置!? なにがねじれているんだろう・・・・
教科書で「ねじれの位置」について調べてみると、
空間内の2直線が、平行でなく、交わらないとき、その2直線は、ねじれの位置にあるといいます。
ってかいてあるね。
つまり、
ねじれの位置は「2つの直線の位置関係」の1種
ってことなんだ。

そこで今日は、
「ねじれの位置」の直線をみつける方法を3ステップで解説していくよ。
よかったら参考にしてみてね。
ねじれの位置をみわける3つのステップ
ねじれの位置は、
空間内における「2直線の関係」のことだったね。
「ねじれの位置」以外にどんな直線の関係があるのかっていうと、
- 交わる
- 平行である(同じ平面上で)
という他の2つがあるんだ。
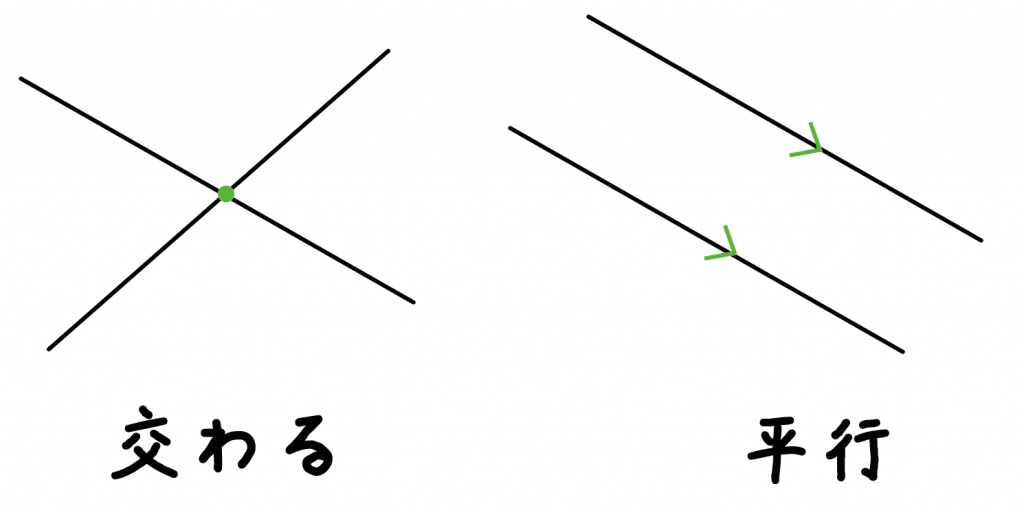
だから、「ねじれの位置」にある直線をみわけるためには「交わらない」し、「平行じゃない」位置関係にある直線をさがせばいいんだ。
つまり、
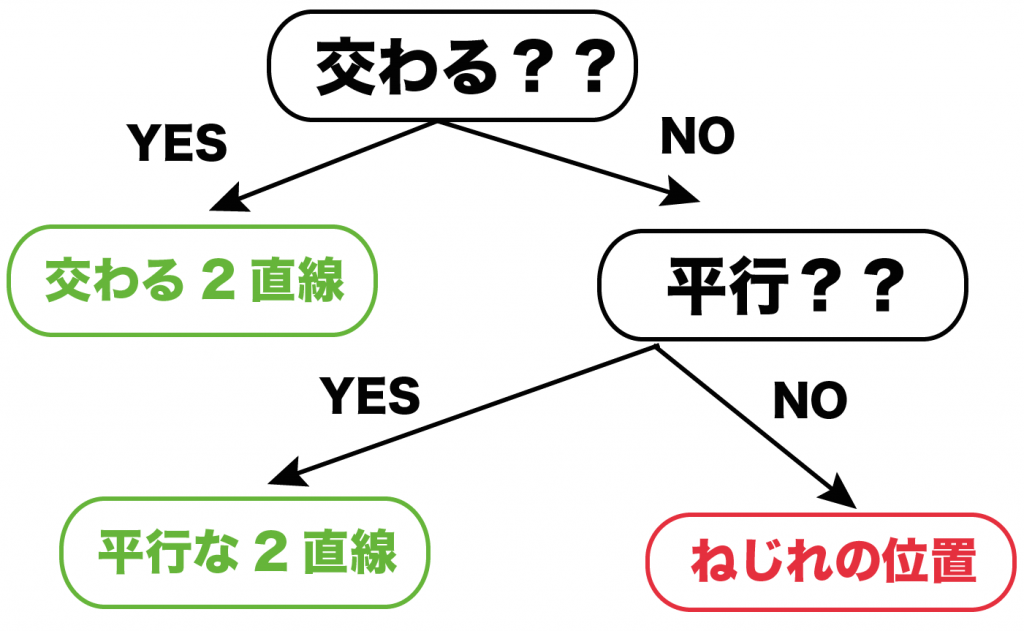
- 交わるかどうか??
- 平行かどうか??(同じ平面上で)
という2つの項目でチェックしてやればいい。
それで、ある直線と交わらないし、平行じゃない直線がでてくるはず。それが「ねじれの位置」にある直線ってことになるんだ。
つぎの問題を解きながら「ねじれの位置」の見分け方をみていこう。
例題
つぎの立方体で直線EFと「ねじれの位置」にある直線をすべてあげてくれ。
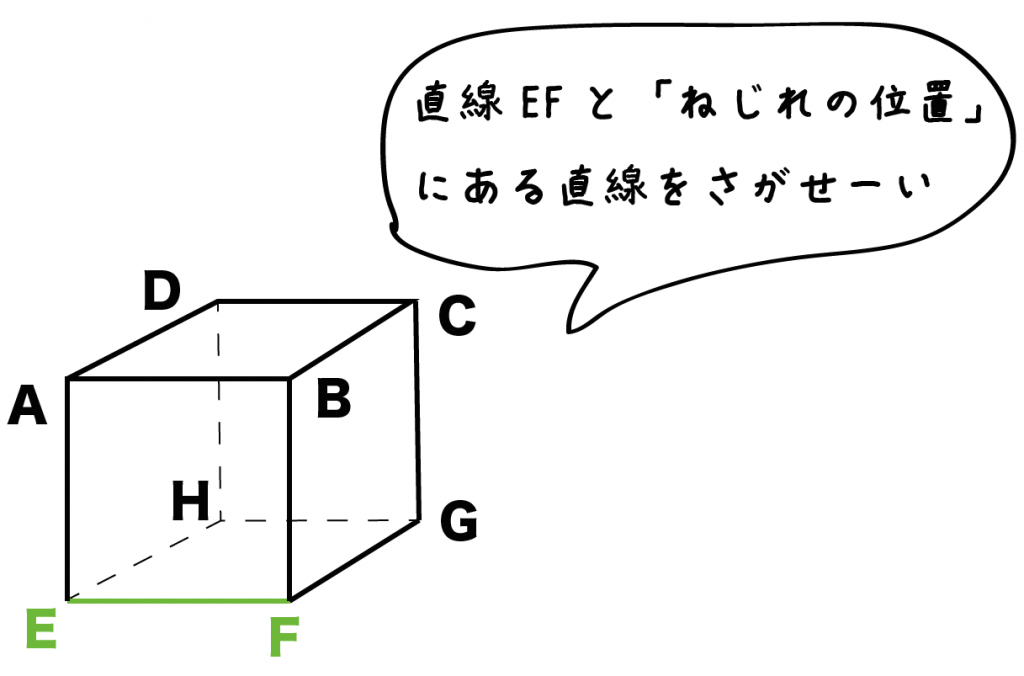
つぎの3ステップで「ねじれの位置」の直線をさがそう!
Step1. 「交わる直線たち」をみつける!
交わっている直線は「ねじれの位置」の関係じゃないんだ。そいつらは「交わっている」という関係になっているよ。
だから、
交わっている直線たちを選択肢からはずしちゃおう!
もう部屋の隅にでも置いておいてくれ。
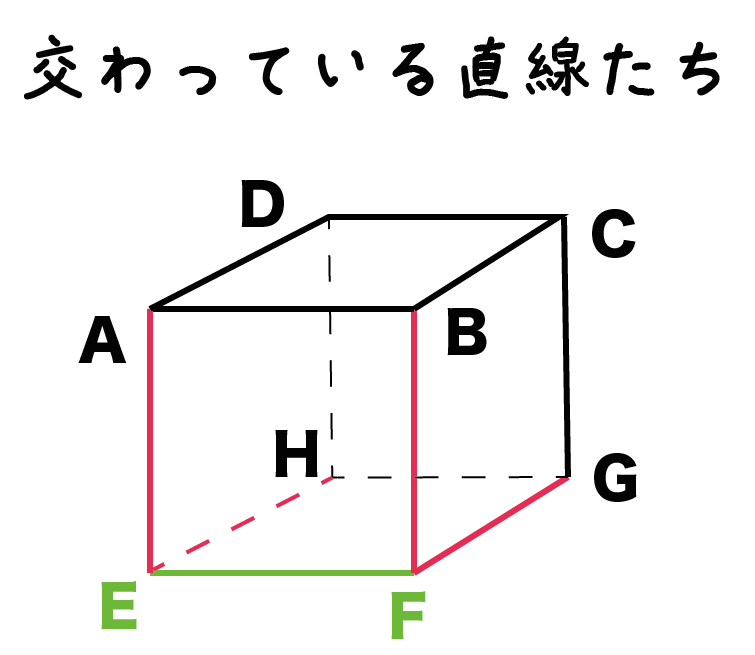
例題でいうと、
直線EFと交わっている直線はつぎの
- 直線AE
- 直線EH
- 直線BF
- 直線FG
の4つだね。「E」か「F」がふくまれるすべての辺がアウトってことさ。
こいつらは「ねじれの位置」なんかでもなんでもない!
Step2. 「平行な直線たち」をみつける!
同じ平面上で平行な直線も「ねじれの位置」の関係になってない。選択肢からはずしてしまおう。
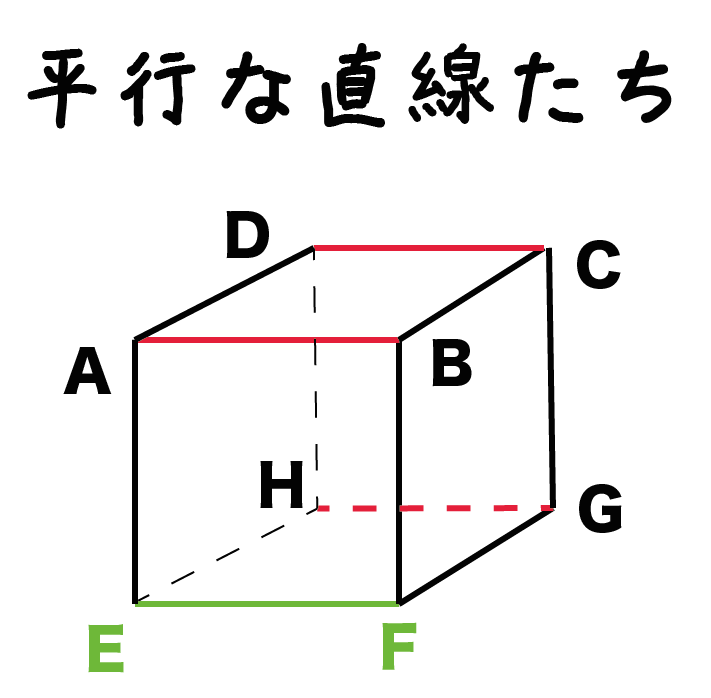
例題でいうと、
- 直線AB
- 直線DC
- 直線HG
が直線EFと同じ平面上で平行になっているよ。
どうやったら「同じ平面上で平行になっているか」を確認できるんだろう??
じつはとっておきの方法を開発しちゃったんだ。それは、
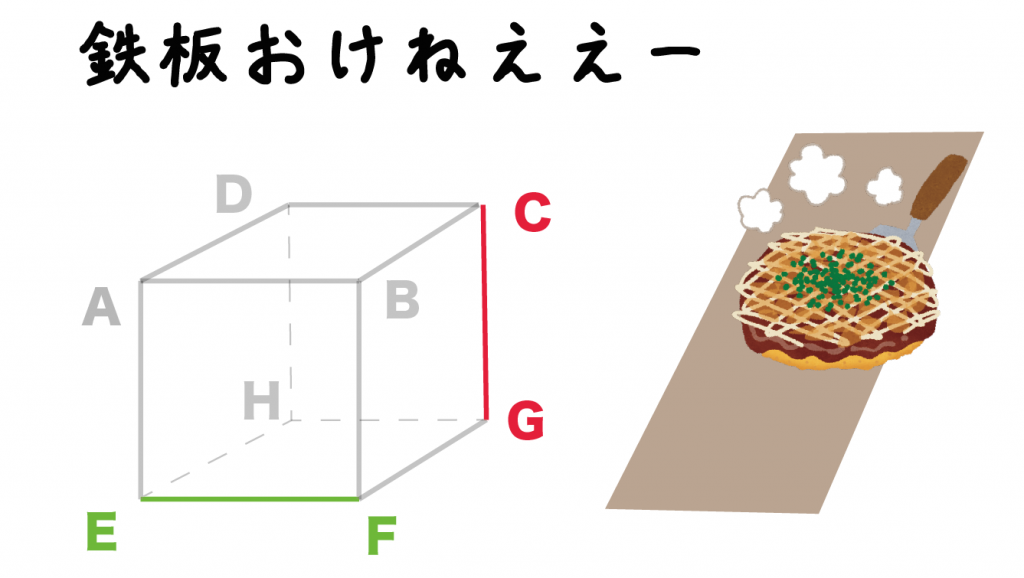
2つの直線の上に鉄板を置いて料理できるか??
を考えてみる方法さ。
たとえば例題の、
直線DCとEFが「同じ平面で平行になっているか」を確認してみよう。
この2つの直線の上にアツアツの鉄板をおいて、
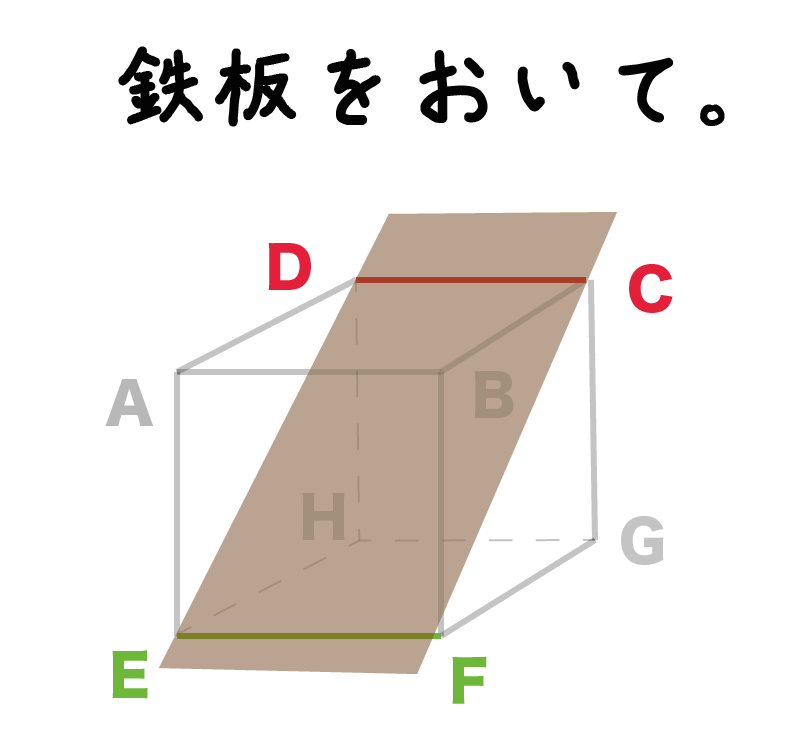
お好み焼きやホットケーキを料理できるか??
って考えてみよう。
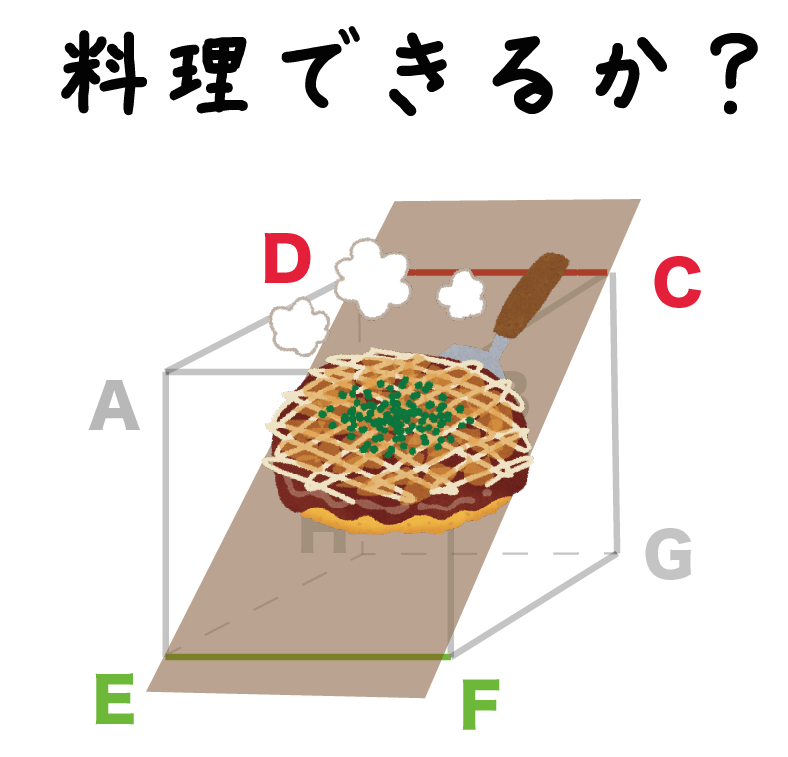
ようは、鉄板という平面を2直線上においたときに、料理ができるぐらいに安定しているかどうか、ってことさ。
それじゃあ、辺CGと辺EFをみてみよう。
こいつらの上にはどう頑張っても鉄板は置けないね。 よほどバランス感覚のあるコックじゃなきゃ無理だ。あくまでも想定するのはアマチュアコックさ。
平行な直線をみつけられないときはこの方法で突破してみよう!
Step3. 残った辺がすべて「ねじれの位置」にある直線
最後に「交わらない」「平行じゃない」直線をすべて洗い出してみよう。
こいつらが「ねじれの位置にある」直線ってことになるんだ。
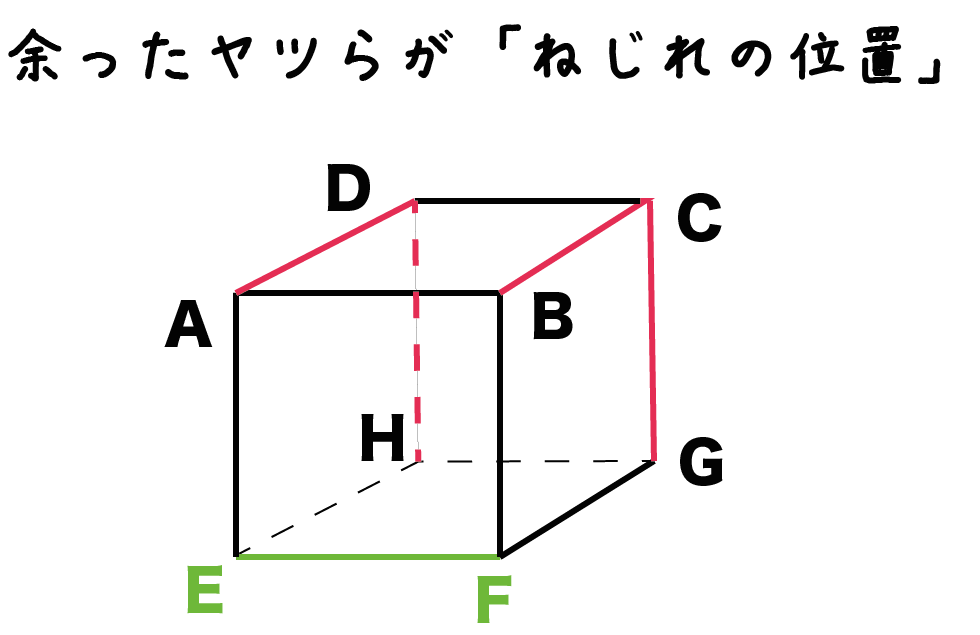
例題でいうと、
- 直線AD
- 直線BC
- 直線DH
- 直線CG
の4つの直線たちだね。こいつらぜんぶが、
直線EFとねじれの位置にある
ってことが言えるんだ! やったね。
まとめ:「ねじれの位置」は消去法でさがすっ!
空間図形の山場である「ねじれの位置」。
名前が名前だけに、問題をだされたら混乱しちゃうかも。 ただ、この記事で紹介したように、
- 交わる直線をはぶく!
- 平行な直線をはぶく!
というふうに、
「ねじれの位置じゃない直線たちをみつけて排除する!」
だけでいいんだ。
ゆっくり焦らず、ひとつひとつの直線について「ねじれの位置」を疑ってみてね。
そんじゃねー
Ken