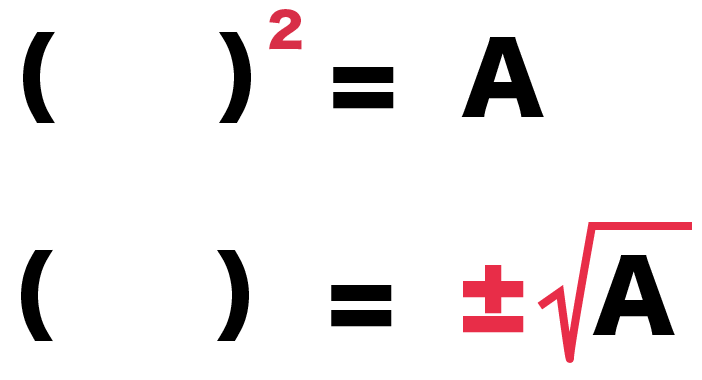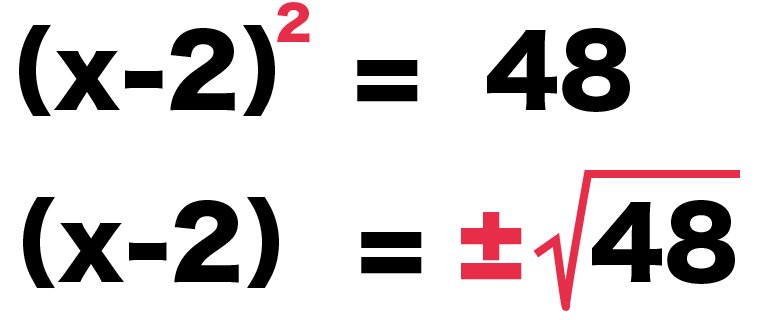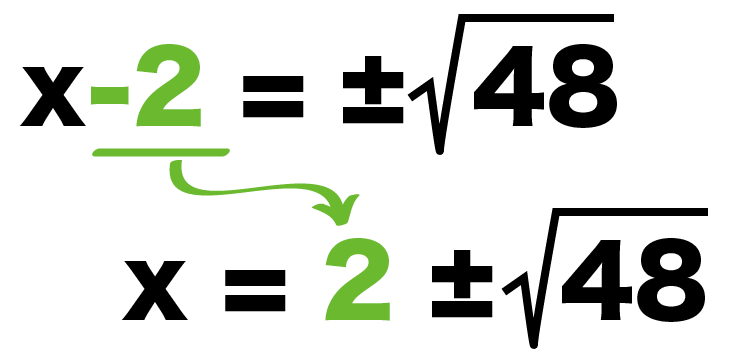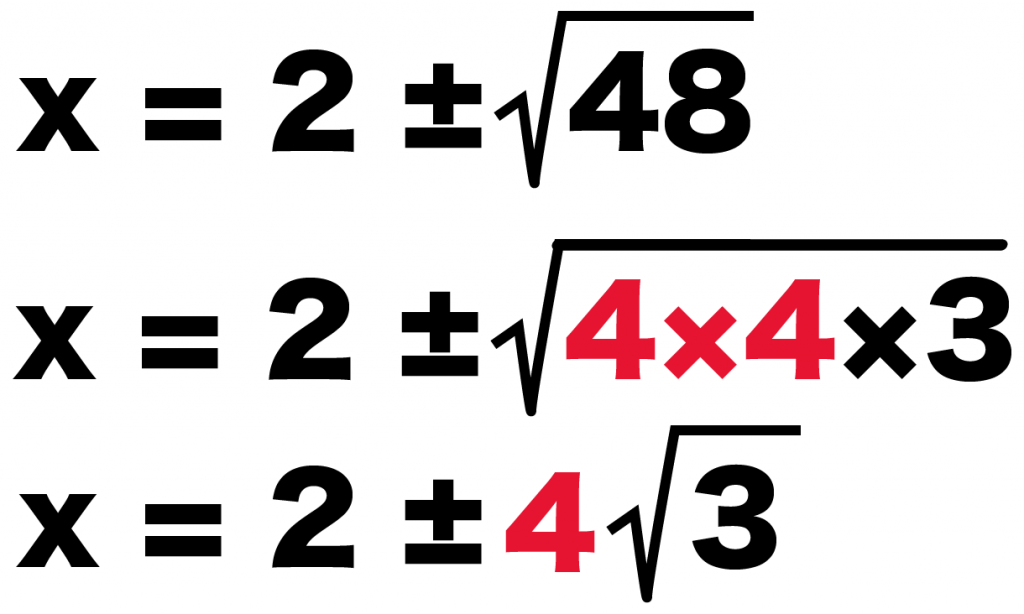平方根をつかった二次方程式の解き方？？
こんにちは！この記事をかいてるKenだよ。天にのぼりたいね。
二次方程式の解き方にはいろいろある。
因数分解の公式をつかったり、
解の公式をつかったり、
たすきがけの因数分解をつかってみたり、、、、
と大忙しだ。
ぶっちゃけ、どの解き方を使えばいいかわからんよね？？
今日は、もう1つ新しい2次方程式の解き方を紹介するよ。
その名も、
平方根をつかった二次方程式の解き方だ。
2次方程式の基礎だから、しっかりおさえておこうね。
平方根をつかった二次方程式の解き方がわかる4ステップ
さっそく、平方根をつかった解き方を紹介していくよ。
つぎの練習問題をといてみよう。
練習問題
つぎの二次方程式を解きなさい。
（x-2）^2 -48 = 0
Step1. 移項する
「（）の2乗」以外を右辺に移項しちゃおう。
例題でいうと、
48
が（）の2乗以外の項だね。
こいつを右辺に移項してやると、
（x-2）^2 -48 = 0
（x-2）^2 = 48
になるね。
Step2. 二乗をとる
つぎは左辺の2乗をとってみよう。
左辺の2乗をとるだけじゃなくて、その分、右辺を「左辺の平方根」にしてあげてね。
つまり、
右辺に±とルートをつければいいのさ。
練習問題でもおなじ。
左辺の2乗をとって、右辺を「左辺の平方根」にしてやると、
（x-2）^2 = 48
（x-2）= ±√48
になるね。
Step3. 移項する
つぎはx以外を右辺に移項しよう。
最終的に「x＝」にもっていきたいからね。
練習問題の左辺には、
-2
っていうx以外の項が残ってるね。
こいつを右辺に移項すると、
（x-2）= ±√48
x = 2±√48
になる。
Step4. ルートを簡単にする
最後にルートを簡単にしてあげよう。
ルートの中身の「2乗の因数」を外にだせばいいんだったね？？
やんなくても間違いじゃないけど、
やったほうが計算の余地が確認できてスッキリするよ。
練習問題のルートの、
±√48
に注目してみて。
ルートのなかの「48」を素因数分解してみると、
48 = 2×2×2×2×3
になるよね？？
ってことは、
2の2乗（4のこと）
を√の外にとりだせそうだ。
さっそく、√48を簡単にしてやると、
x = 2±√48
x = 2 ± 4√3
になるね。
これで二次方程式がとけちゃったんだ。
平方根をつかうと簡単に解けるね。
まとめ：平方根をつかった二次方程式の解き方は移項しまくれ！
平方根をつかった二次方程式は4ステップでとけちゃうよ。
- 移項
- 二乗をとる
- 移項
- ルートを簡単にする
みたかんじ、移項できればとけそう。
ガンガン平方根をつかっていこう。
そんじゃねー
Ken
