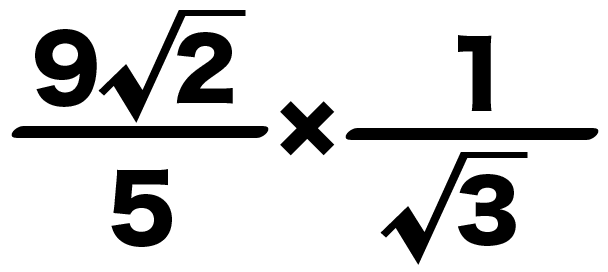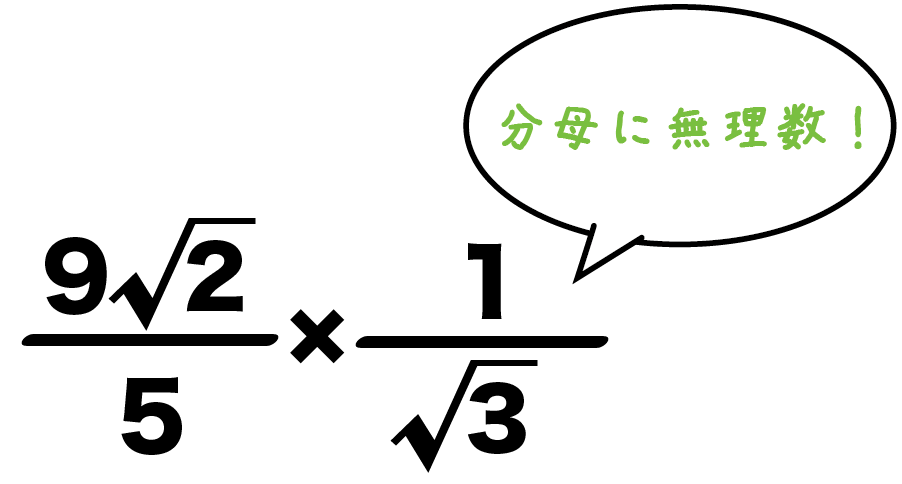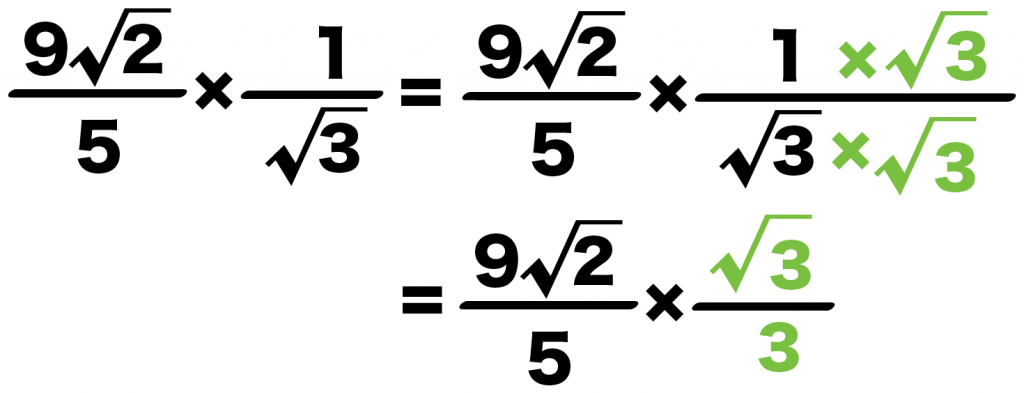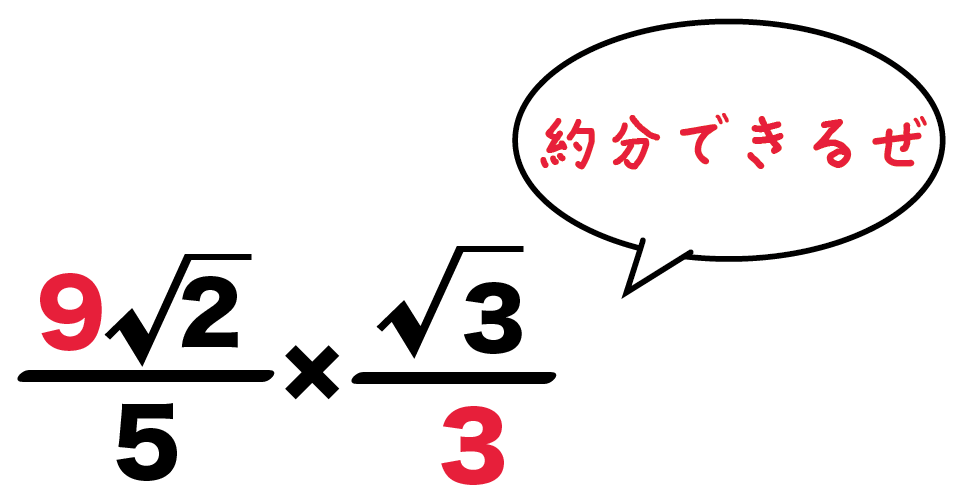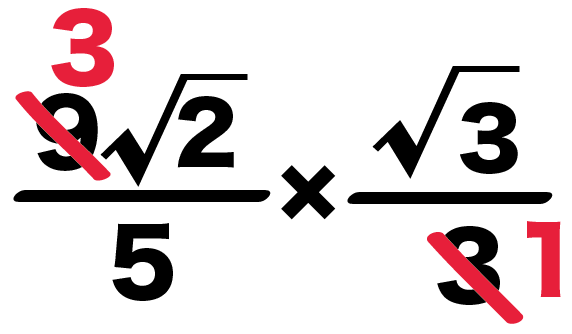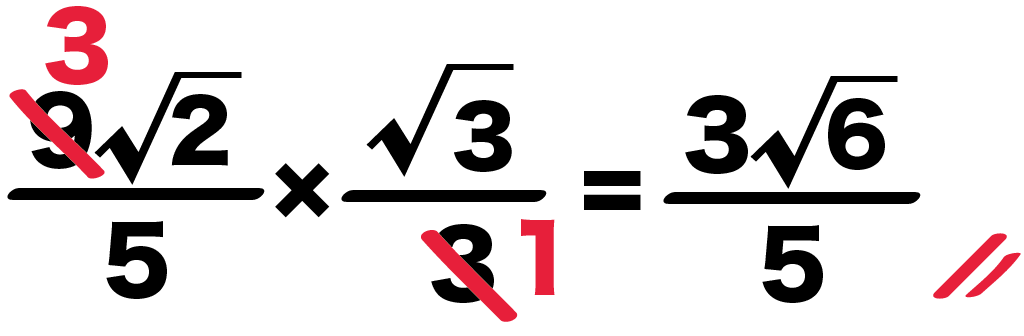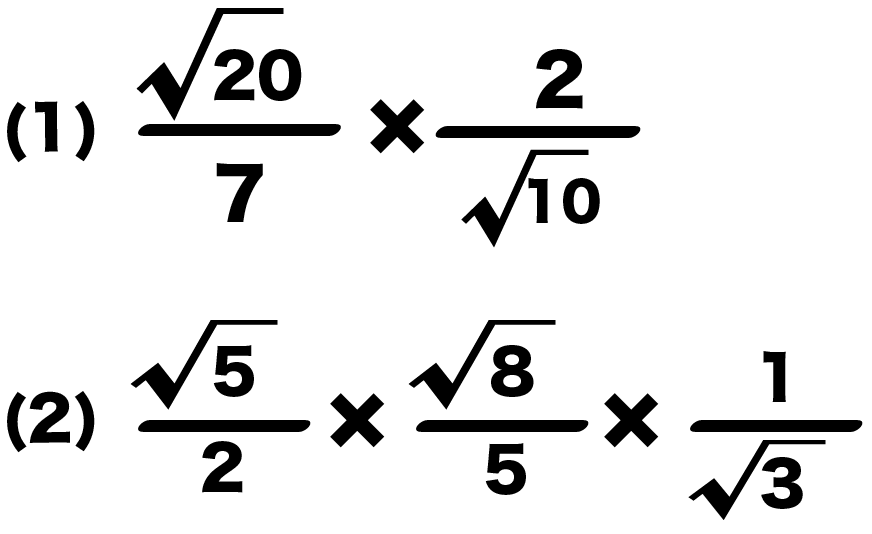ルート分数の掛け算の計算方法は？？
こんにちは！この記事をかいているKenだよ。野菜摂取したいね。
ルート計算でヤッカイなのは、
分数がまじった問題
だ。
シンプルな平方根の計算ならいけるんだけど、
分数がからむとヤッカイだ。
そこで今日は、
ルート分数の掛け算の計算方法
を3ステップで解説するよ。
よかったら参考にしてみて。
ルート分数の掛け算の計算方法がわかる3ステップ
例題をといていこう。
例題
つぎの平方根の計算をしなさい。
5分の9√2 × √3分の1
ルート分数の掛け算は3ステップでとけちゃうよ。
- 分母の有理化
- 約分
- 分母・分子同士をかける
Step1. 分母を有理化する
分母を有理化しよう。
答えは有理化しなきゃいけないから、先にやっちまうのがベストだ。
⇒ 分母の有理化の方法はこちら
例題では「√3分の1」の分母にルートがあるね？？
こいつを有理化しちゃおうぜ。
分母から√3を消し去るために、分母・分子に√3をかけてみて。
すると、
5分の9√2 × √3分の1
= 5分の9√2 × 3分の√3
になるね。
Step2. 約分する
もし、分母・分子に公約数があるなら約分すればいい。
例題でいうと、
- 5分の9√2 の分子の「9」
- 3分の√3の分母「3」
が約分できそうだ。
なぜなら、
「9」と「3」の公約数は3だからね。
こいつらを約分してみると、
5分の9√2 × 3分の√3
= 5分の3√2 × 1分の√3
になるね！
Step3. 分母・分子どうしを掛け算
分母・分子を掛け算しよう。
ルートの掛け算では、中身を掛け算しちゃえばよかったね？？
⇒ルートの掛け算の仕方はこちら
例題でも計算してみると、
5分の9√2 × 3分の√3
= 5分の3√2 × 1分の√3
= 5分の3√6
になるね。
おめでとう！
ルート分数の掛け算もバッチコイだ。
練習問題：ルート分数の掛け算は有理化をまず先に！
最後に、計算問題をといてみて。
練習問題
つぎの平方根をふくむ計算をしなさい。
- 7分の√20 × √10分の2
- 2分の√5 × 5分の√8 × √3分の1
⇒練習問題の解答はこちら
どう？？うまくとけたかな？！
問題をといて掛け算に慣れていこう。
そんじゃねー
Ken
