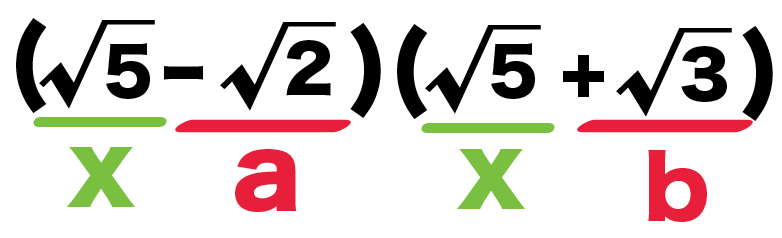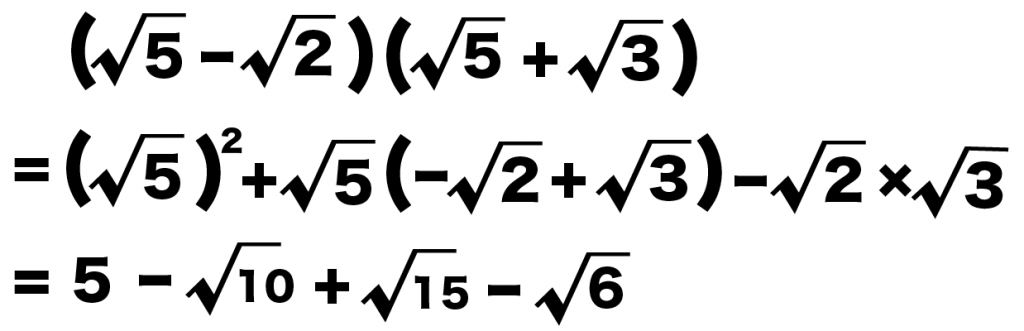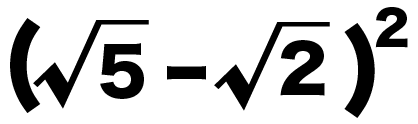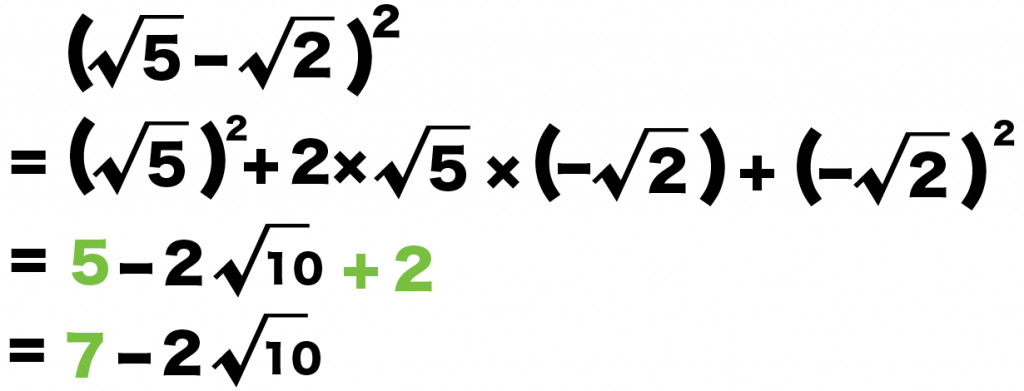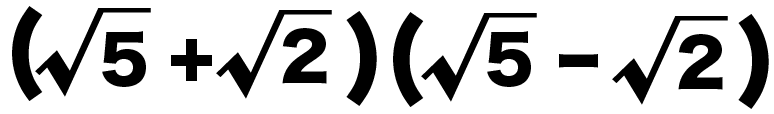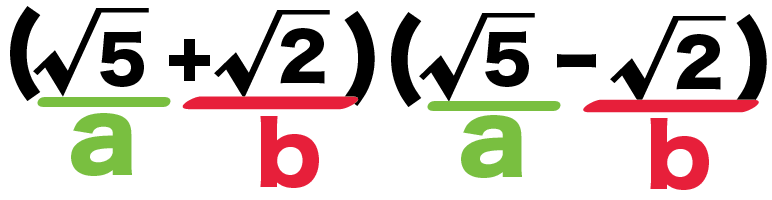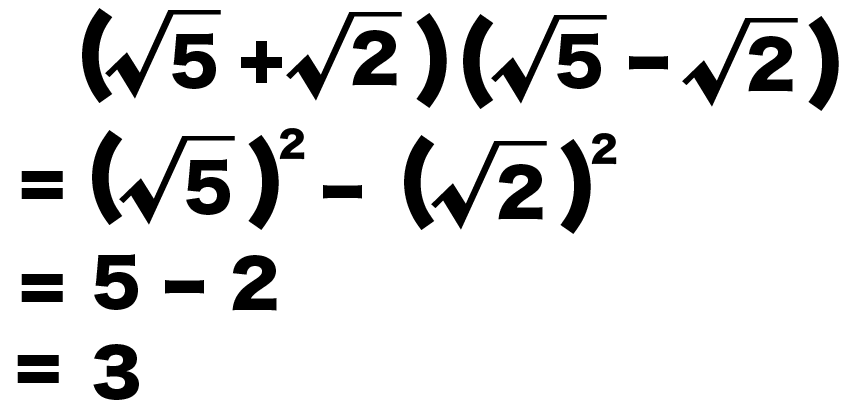【ルート計算】展開公式をつかう3つの平方根問題の解き方
ルート・平方根で展開公式はつかえるの??
こんにちは、この記事をかいてるKenだよ。ワッフルにもいろいろだね。
平方根の計算問題をたくさんといてきたね。
たぶんね、これからもルート計算をガシガシやっていくよ。
悲しいけどこれが現実だ。
んで、その計算問題のなかには、
展開公式をつかう問題
がでてくると思うんだ。
えっ。
展開の公式なんて忘れてたって?!?
ノンノン。
展開公式にはつぎの3つがあったよね。
- (x+a) (x+b)の展開
- 平方の公式
- 和と差の積
こいつらは平方根の計算式につかってもOK。
むしろ、ガンガン使って欲しいね。
今日は、
3つの展開公式を使った平方根の計算問題をといていこう!
=もくじ=
- 展開公式をつかう問題の基本
- 3つのルート計算問題
ルートの式に展開公式をつかう問題の解き方
展開公式をつかう問題はシンプル。
つぎの2ステップでとけちゃうよ。
- 展開公式をつかう
- ルートの足し算・引き算する
ようするに、展開公式で簡単にして、いつも通り計算ってわけだ。
今日は展開公式を3つ使ってみよう。
- (x+a) (x+b)の展開
- 平方の公式
- 和と差の積

問題1. 「(x+a)(x+b)の展開」
まず展開公式1つめの、
(x+a)(x+b) = x^2 + (a+b)x + ab
をつかおう。
たとえば、つぎのような計算問題だ。
練習問題
つぎの平方根の計算をしなさい。
( √5 – √2 ) (√5 + √3 )
この計算式では、2つの()のなかに、
√5
があるよね??
で、そいつらに、
- -√2
- √3
がそれぞれ足されてる。
ってことは、展開公式でいうと、
- x = √5
- a = -√2
- b = √3
になってるわけさ。
(x+a)(x+b)の展開公式をつかうと、
( √5 – √2 ) (√5 + √3 )
= √5^2 +√5 (-√2 + √3) – √6
= 5 -√10 + √15 – √6
になるね。
さてと・・・ルートの足し算をっと・・・
っていいたいところだけどね、これ以上計算できないんだ。
なぜなら、
ルートの中身がぜんぶ違うからね。
これで計算終了だ!
問題2. 「平方の公式」をつかう
おつぎは平方の公式の、
(a+b)^2 = a^2 +2ab + b^2
をつかってみよう。
つぎの例題をといてみて。
( √5 – √2 )^2
平方の公式で展開すると、
( √5 – √2 )^2
= ( √5 )^2 – 2×√5 × √2 + (√2 )^2
= 5 -2√5 +2
になる。
あとはルートの足し算・引き算するだけ。
数字同士でまとめると、
( √5 – √2 )^2
= ( √5 )^2 – 2×√5 × √2 + (√2 )^2
= 5 -2√5 +2
= 7 -2√5
になるね。
これで計算終了だ^-^
問題3. 「和と差の積」をつかう
最後は、和と差の積の公式をつかってみよう。
(a+b)(a-b) = a^2 – b^2
つぎの計算問題をといてみよう。
練習問題3.
つぎの平方根の計算をしなさい。
( √5 + √2 ) (√5 – √2 )
公式にあてはめると、
- a = √5
- b = √2
になるはずだ。
なぜなら、
2つの()に√5があって、√2は符号違いだからね。
和と差の積の公式で計算すると、
( √5 + √2 ) (√5 – √2 )
= ( √5 )^2 – ( √2 )^2
= 5-2
になるね。
あとはルートの足し算・引き算だ。
この計算式だと、ルートもくそもない。
整数同士で計算してやると、
( √5 + √2 ) (√5 – √2 )
= ( √5 )^2 – ( √2 )^2
= 5-2
= 3
になるね!
これで計算終了だ。
まとめ:ルートの計算式だろうが展開公式つかおうぜ!
平方根の式に展開公式つかえたかな??
- (x+a) (x+b)の展開
- 平方の公式
- 和と差の積
を使い分けよう。
あとは、問題演習あるのみ。
展開しまくっていこう。
そんじゃねー
Ken