正三角形の高さの求め方の公式はあるの？？
こんにちは！この記事をかいているKenだよ。ごぼうがうまいね。
正三角形の高さの求め方には公式があるよ。
それも、むちゃくちゃシンプル。
正三角形の1辺をa とすると、その高さは、
√3/2 a
で計算できちゃうんだ。
つまり、
（正三角形の1辺の長さ）× √3 ÷2
ってことだね。
たとえば、
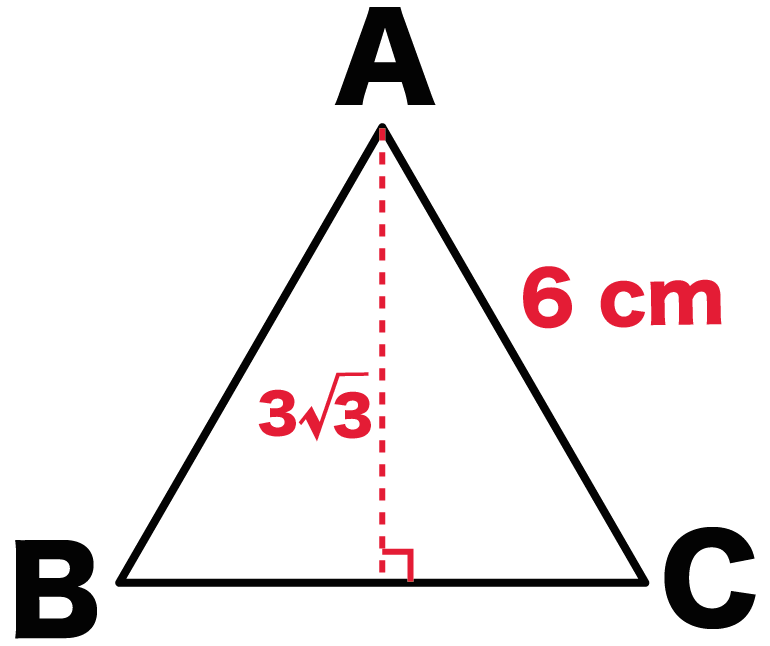
1辺が6cmの正三角形ABCがあったとしよう。
公式で高さを計算すると、
6 × √3 ÷2
= 3√3 [cm]
になる。
ね？
簡単でしょ？？
正三角形の高さの求め方がわかる3ステップ
公式はむちゃ便利。
だけど、
忘れたら何もできなくなっちゃうよね？
だから今日は、
正三角形の高さの求め方を3つのステップで紹介していくよ。
公式をおぼえるのが苦手な人は参考にしてみてね。
例として、1辺6cmの正三角形ABCの高さを求めていこう！
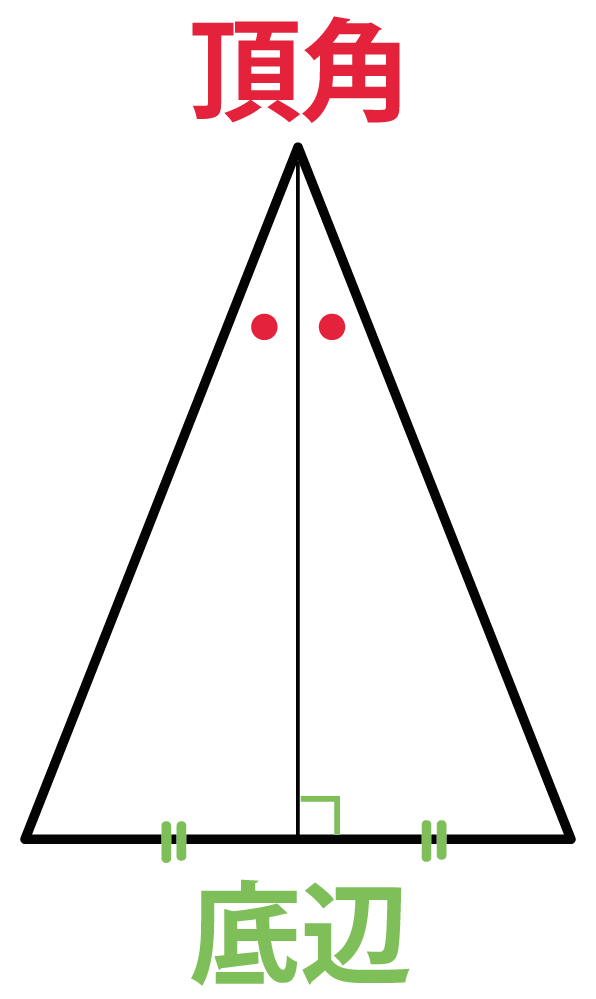
Step1. 頂角の二等分線をひっぱる
頂角から底辺に二等分線をひいてみよう。
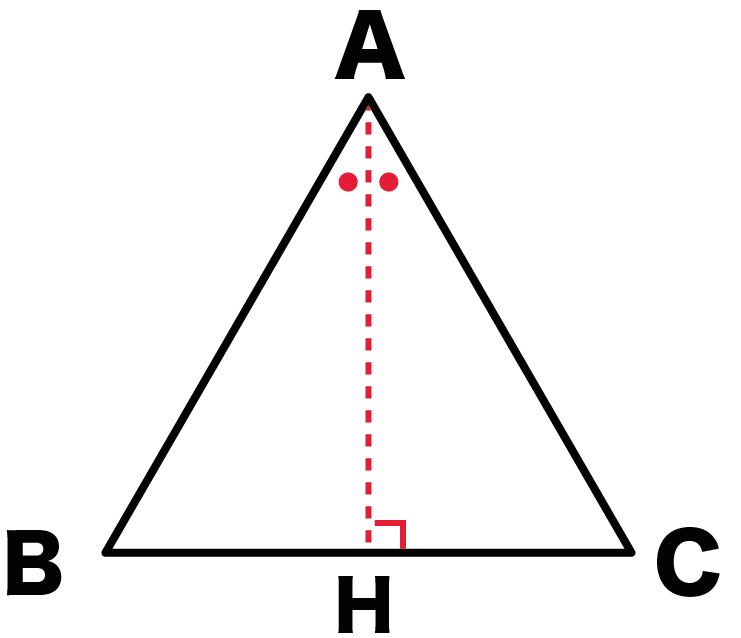
三角形ABCでいうと、
角Aが二等分される直線を、
BCにすーーーっとひけばいいんだ。
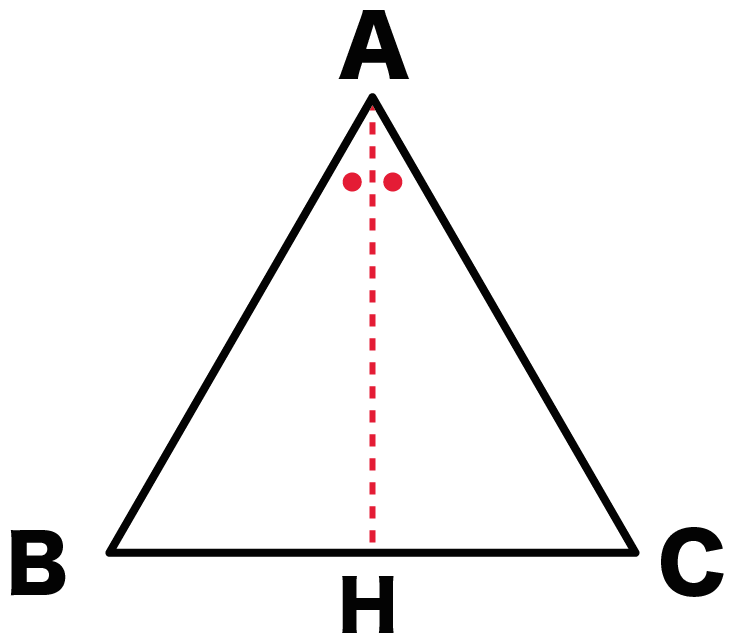
BCと二等分線の交点をHとおくよ。
これが第一ステップさ。
Step2. 二等辺三角形の性質をつかう！
頂角の二等分線は底辺を垂直に2等分する
をつかってやろう。
正三角形は二等辺三角形の仲間。
だから、性質がつかえちゃうんだ。
これをつかえば、
AHはBCの垂直二等分線になっているはず。
よって、
AH ⊥ BC
になるね。
Step3. 直角三角形の比をつかう！
直角三角形の比で高さを計算しよう。
二等分線でできた、
小さい三角形に注目して。
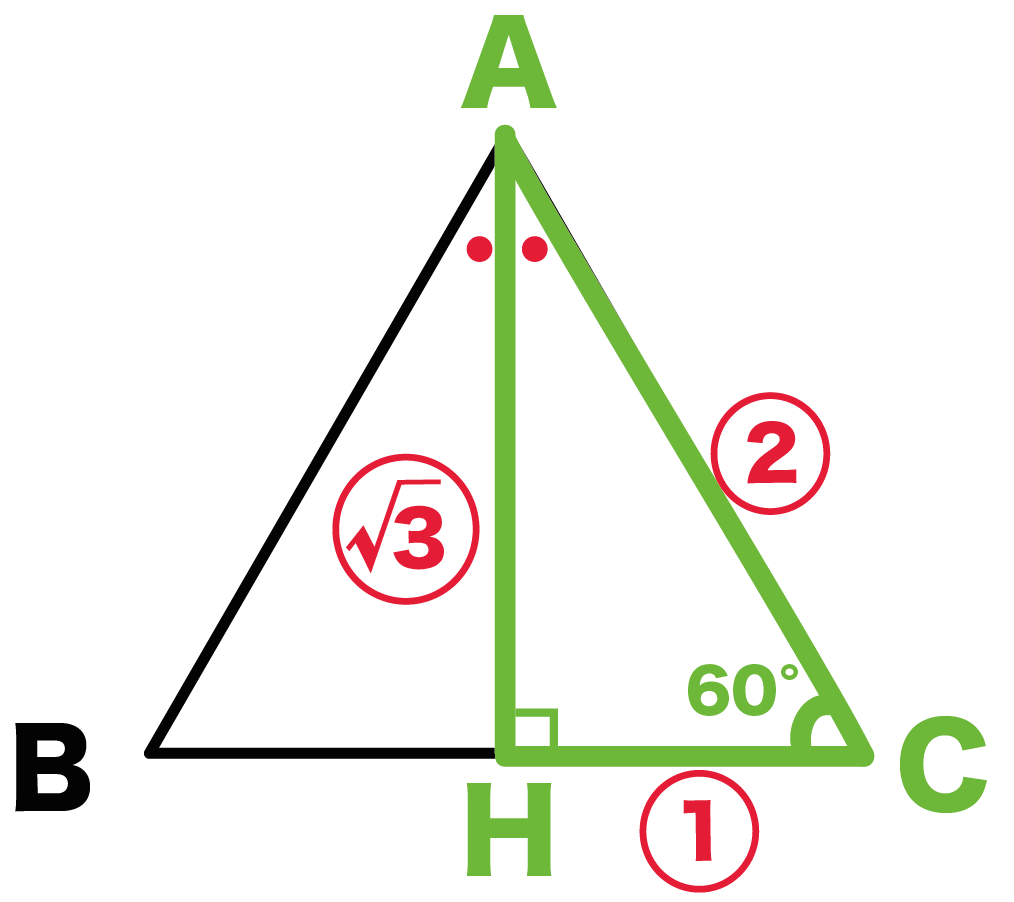
△ABCでいうと、△ACHだね。
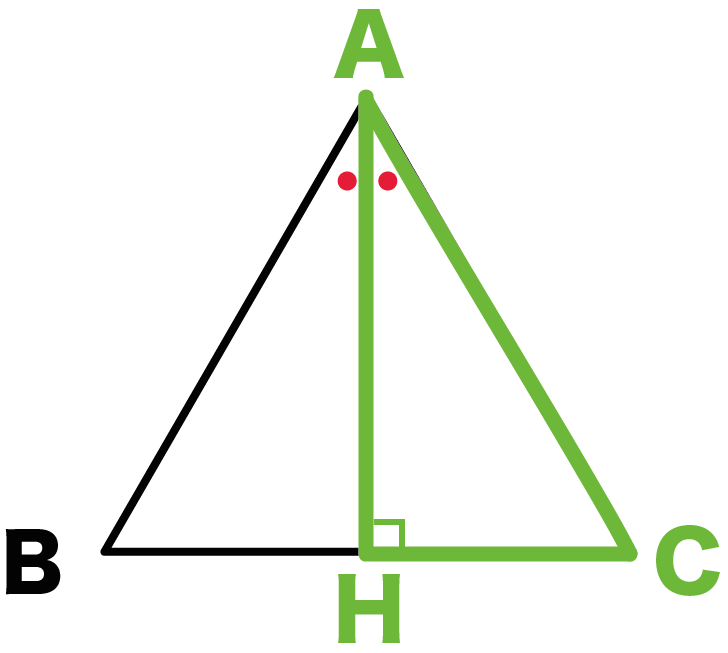
角Cは60°だよね？？
だって、
正三角形の角度の大きさはぜーんぶ60°だからさ。
だから、
直角三角形ACHの各辺の比は、
1:2:√3
になっているはずだ。
AC = 6 cmだから、比をつかって高さAHを計算すると、
AH = 6 ×√3/2
= 3√3
になる。
これで正三角形の高さが計算できたね。
まとめ：正三角形の高さの求め方は比をつかえ！
正三角形の高さはシンプル。
- 頂角から二等分線をひく
- 二等辺三角形の性質をつかう
- 直角三角形の比をつかう
の3ステップでいいんだ。
じゃんじゃん攻略していこう！
そんじゃねー
Ken
