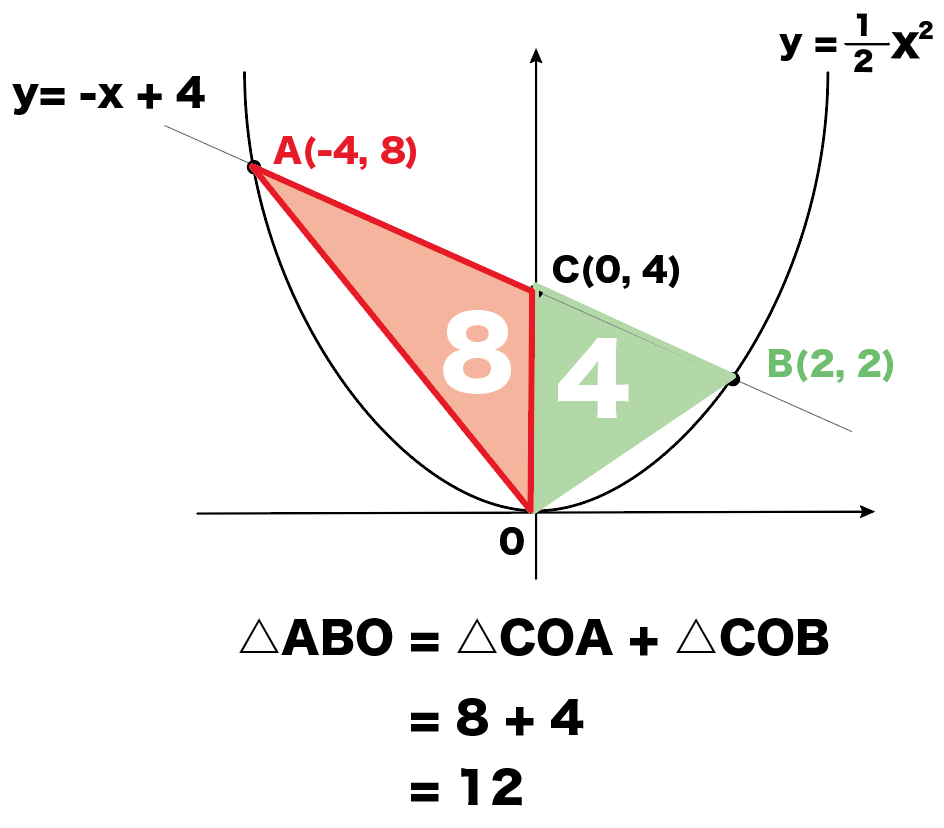
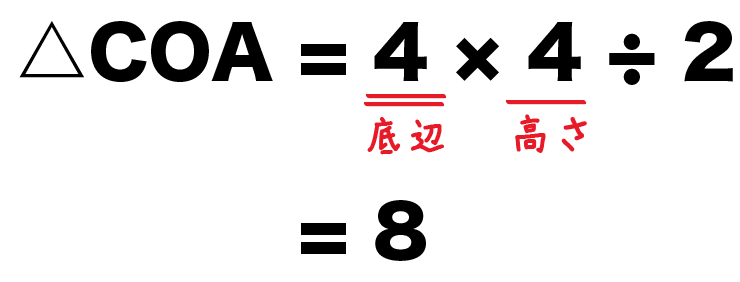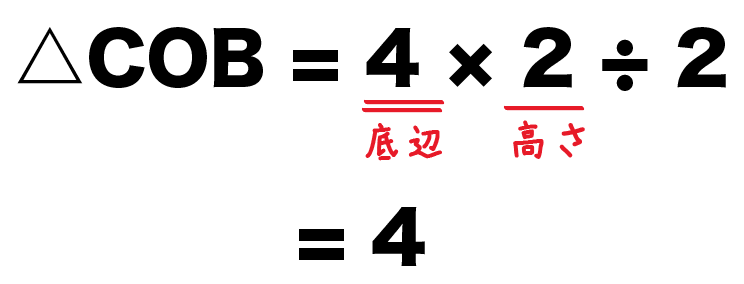二次関数のグラフで三角形の面積を求める問題の解き方の4ステップ
二次関数で三角形の面積を計算しろ??
やあ、ぺーたーだよ。
二次関数のテストでよくでるのは、
三角形の面積を求める問題。
難しいからみんな嫌がるよね??
図形と関数のコラボとかやめてほしいけど、
テストに出てきちゃう。
何とか解けるようにしたいね。
そこで、今日は、
二次関数の三角形の面積の求め方
を3ステップを紹介するよ!
二次関数で三角形の面積を求める4ステップ
つぎの問題をといてみよう!
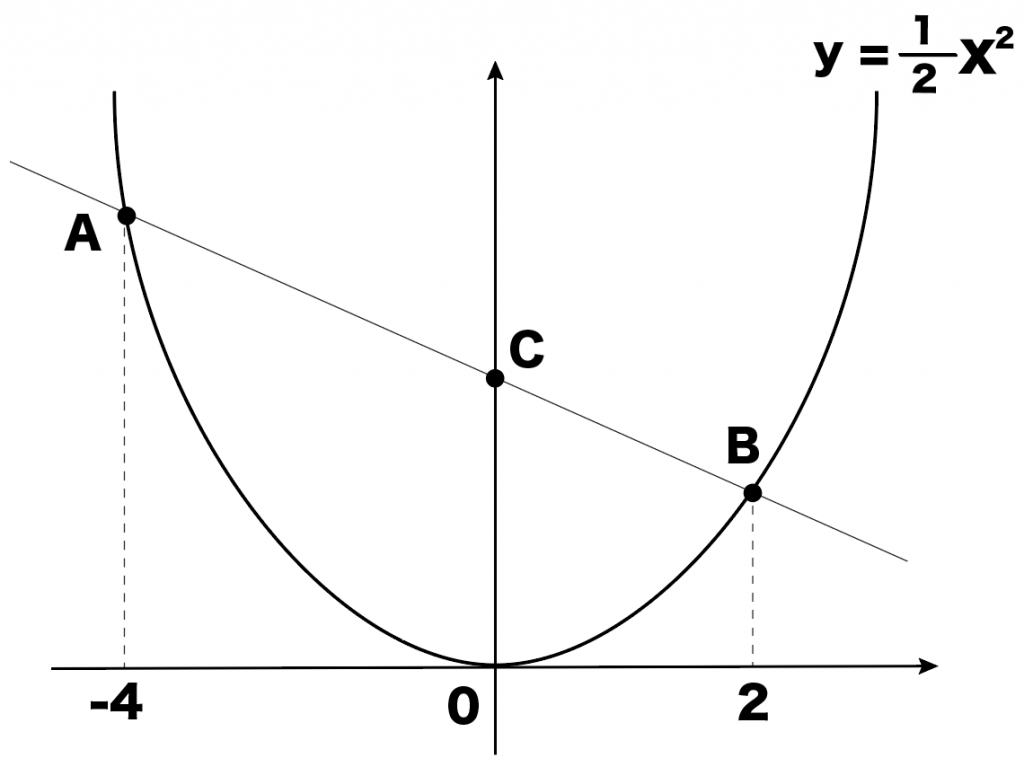
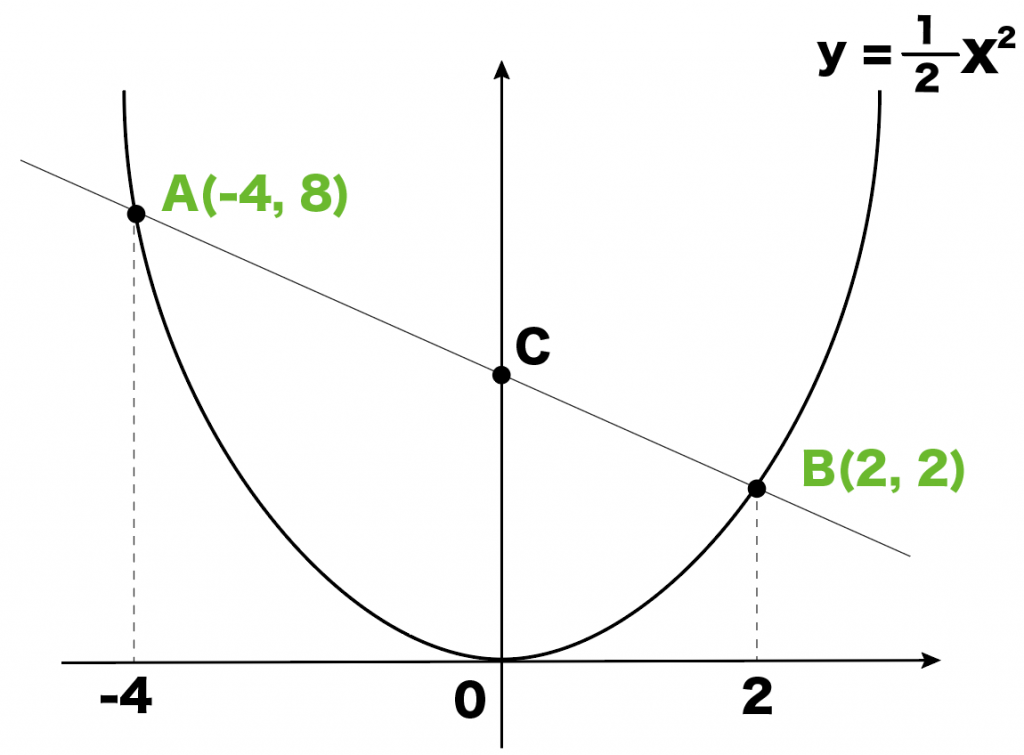
y = 1/2 x² のグラフ上に2点A, Bがあり、
それぞれのx座標は-4と2です。
直線ABとy軸の交点をCとするとき△AOBの面積を求めてください。
3ステップでとけちゃうよ。
- 座標を求めよう
- 三角形を二つに分けよう
- 二つ三角形の面積を求めよう
Step1. 座標を求めよう
まず座標を求めてみよう。
練習問題でいうと、
- 点A
- 点B
- 点C
の3点の座標ね。
この問題では、それぞの点のx座標がわかってる。
だから、
二次関数にxを代入すればいいね。
y = 1/2 x²にそれぞれ代入すると、
- 座標Aのy座標: y = 1/2 ×(-4)×(-4)= 8
- 座標Bのy座標: y = 1/2 × 2 × 2 = 2
になる。
ってことは、
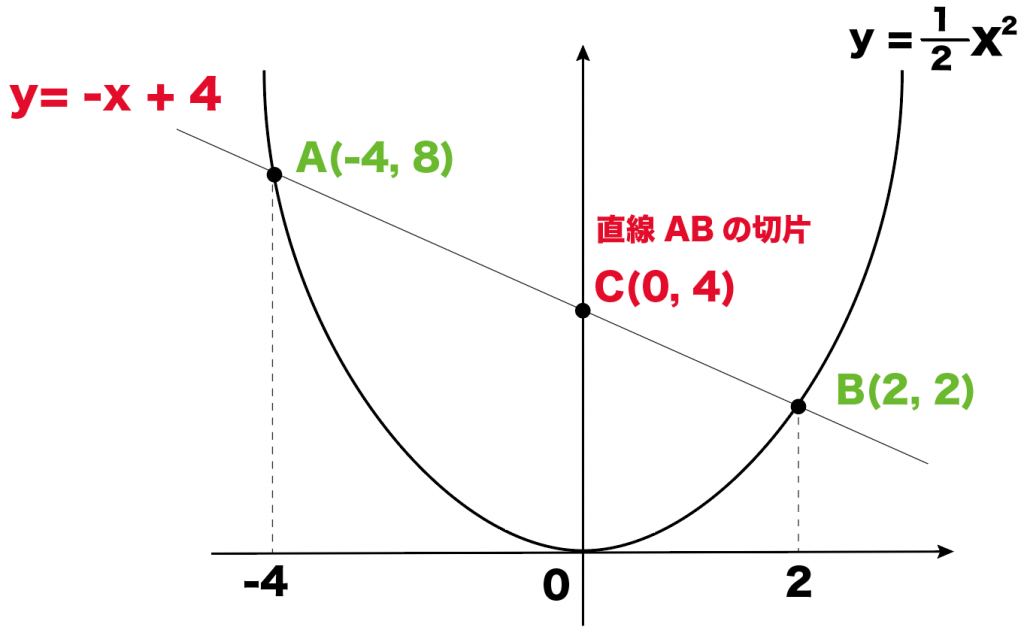
- 座標A:(-4, 8)
- 座標B:(2, 2)
になるはずだ。
あとは点C。
こいつは、直線ABの切片だね??
直線ABの式がわかればCの座標もわかるってわけ。
直線ABの式は2点は、
- 点A(-4, 8)
- 点B(2, 2)
だ。
y=ax+bに代入して連立方程式をつくると、
8 = -4a + b
2 = 2a + b
ってなる。
こいつをとくと、
- a = -1
- b = 4
になるね。
つまり、直線ABの式は、
y = -x + 4
になるんだ。
点CはABの切片だから、
C (0, 4 )になるね。
ちょっと長くなったけど、分かった座標を図に書き込むよ!
Step2. 三角形を2つにわける!
三角形の面積を2つにわけて考えてみよう。
練習問題では、
△AOBの面積
を求めたかったよね??
だがしかし、
そんな三角形見当たらない。
だから自分で、
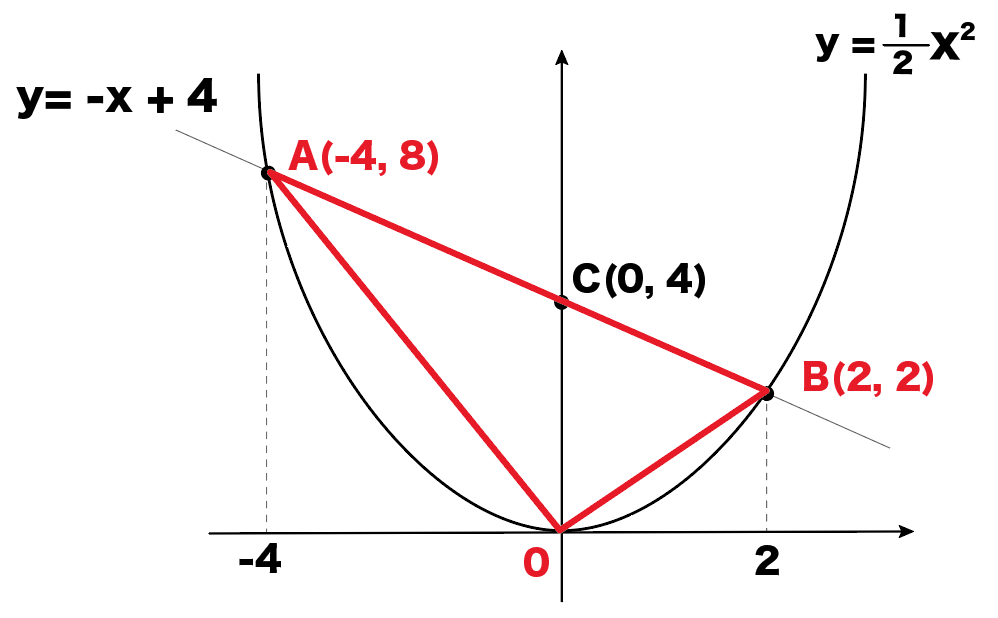
△AOBを書き込むんだ。
すると、こんな三角形ができあがるよ!
さあ、これで三角形の面積を求めよう!
…と言いたいところなんだけど、このままだと難しいんだ。
なぜなら、
底辺も高さもわかってないからね。
じゃあどうすればいいの!?
よーく見ると三角形が見えてこない?
そう!
△AOBで見るんじゃなくて、
三角形を2つに分けて考えるんだ!
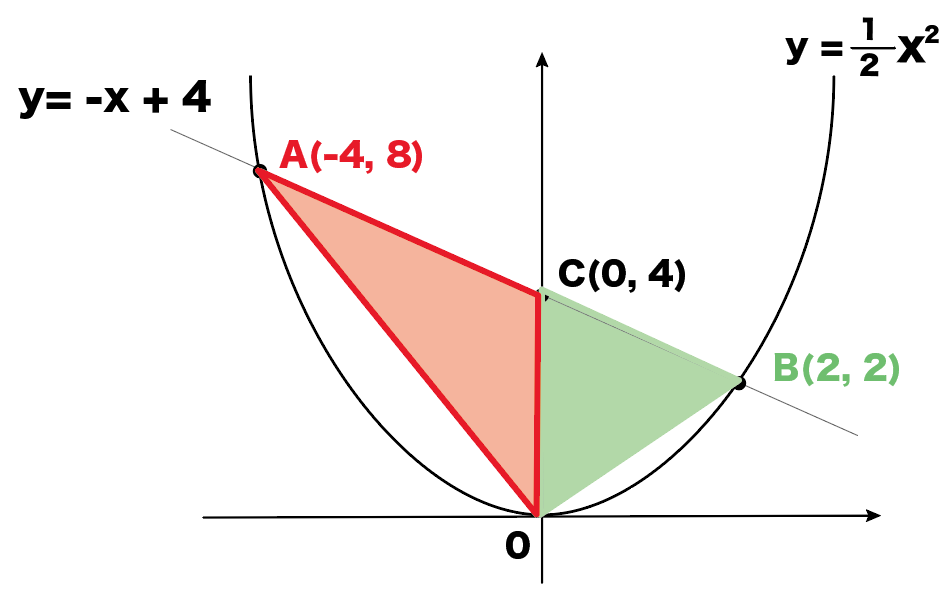
どう分けるかというと…
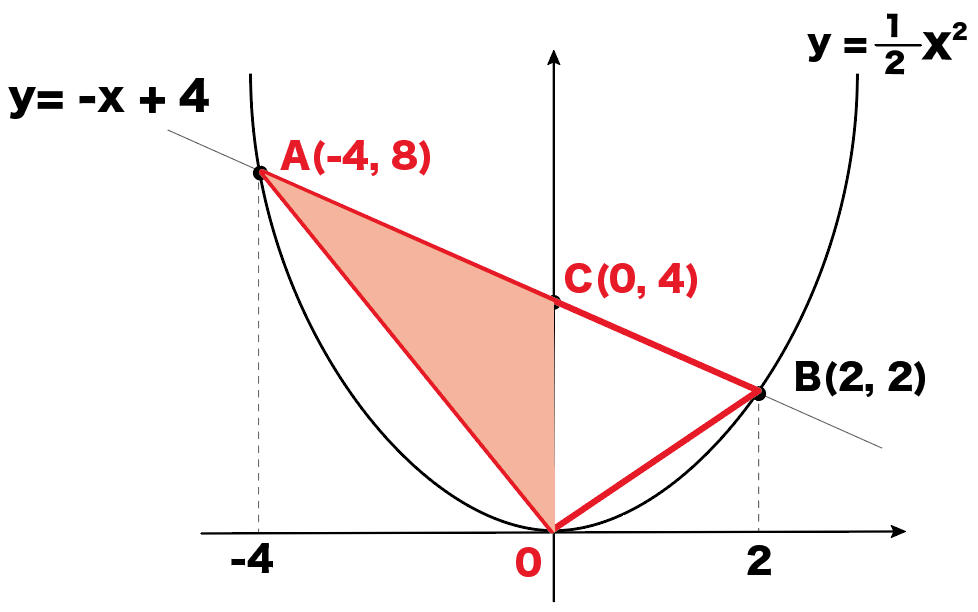
△COAと、
△COBでわけるんだ。
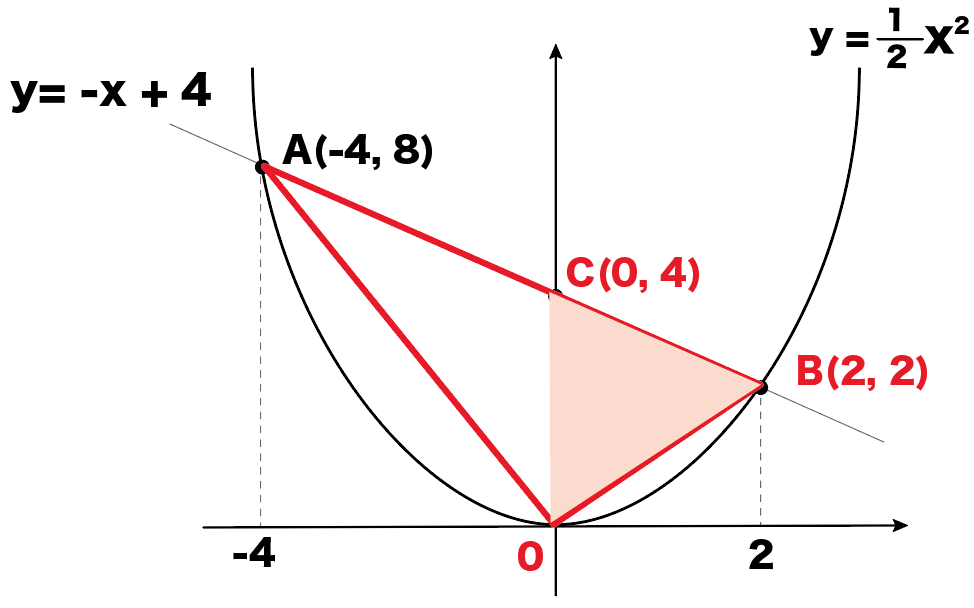
Step3. それぞれの面積を計算
三角形の面積を計算しよう。
わけた2つの三角形の面積をそれぞれ計算すればいいのよ。
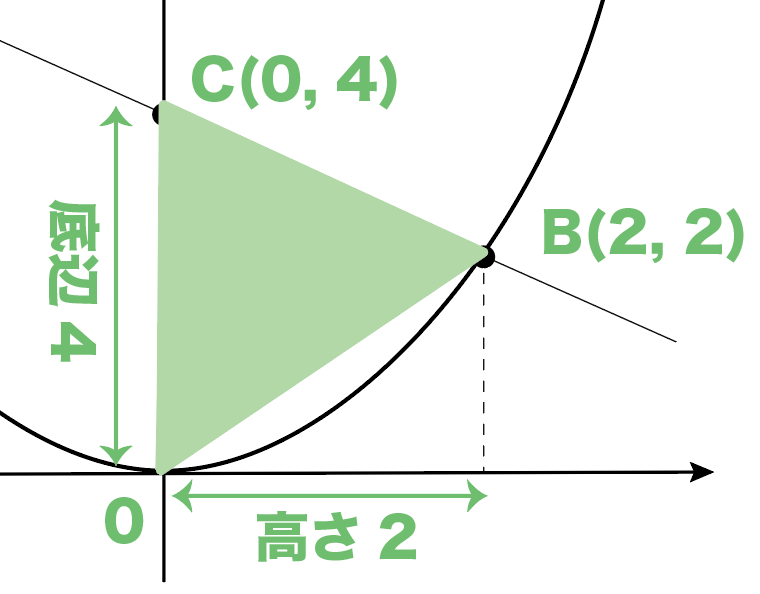
まず△COAの面積。
COを底辺、Aのx座標を高さとしてみてね。
Oのy座標は0、Cのy座標は4だから
底辺=4。
高さは「Aからy軸まで」の長さ。
つまり、Aのx座標のことだから、
高さ=4だね。
三角形の面積の公式は「底辺×高さ÷2」だったよね??
こいつで計算してやると、
△COA
= 底辺×高さ÷2
= 4×4÷2
= 8
になる。
次は△COB。
COを底辺、Bからy 軸までを高さと考えてみると、
△COB
= 底辺×高さ÷2
= 4×2 ÷2
= 4
になるね。
Step4. 三角形の面積をたす
2つの三角形を足しちゃえば終わり!
練習問題でいうと、
△AOB = △COA + △COB
ってわけだね。
実際に計算してみると、
△AOB
= 8 + 4
= 12
になる。
だから答えは12なのさ。
大変だったね。お疲れさま!
まとめ:二次関数の三角形の面積はわけて計算!
二次関数で三角形の面積を求める問題は、
- 座標を求める
- 三角形を分けて考える
の2ステップで大丈夫。
難しいけど、慣れれば絶対に解けるようになるよ。
じゃ、今回はここまで。
じゃあねー
ぺーたー