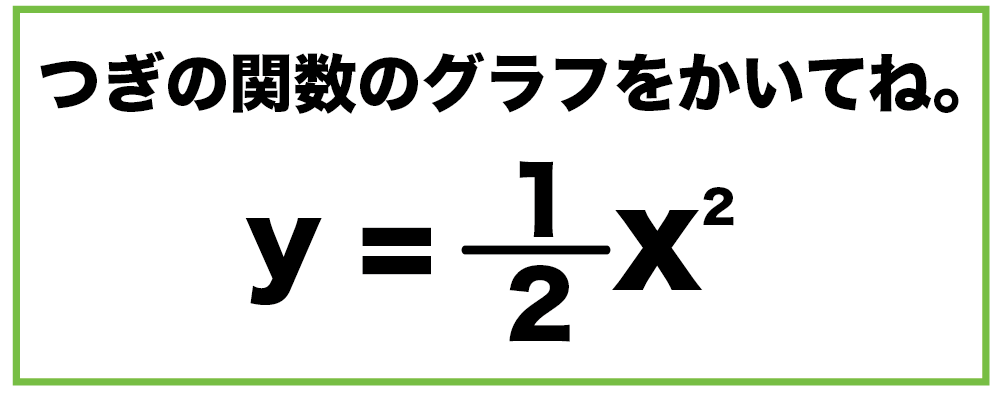二次関数y=ax2のグラフの書き方がわからない！
みんな、元気にしてる？そらだよ☆彡
今日は二次関数y = ax2 のグラフをかくんだ！
どちらかというと、今日は「絵を描く」感覚(^_-)-☆
え？絵を描くの苦手？
大丈夫だよ、グラフは絵とはべつものだし！
いっしょに二次関数y=ax2のグラフの書き方を勉強していこう！！
二次関数y=ax2のグラフの書き方がわかる 3つのステップ
二次関数y=ax2のグラフの書き方はつぎの3ステップ。
- 点をたくさんゲット
- 座標に点をうちまくる
- 点と点をむすぶ
グラフが通る点をたくさんゲットして、
雰囲気で放物線をかけばいいのさ。
「グラフ」はたくさんの値＝「点」の集まりの「線」だよね。
ということは、まずは「値」を求めなきゃ、グラフは描けないよね。
そして今度は、点たちを座標に書き込むことができる。
点を描き込むことができれば、できたも同然！
あとは点と点を結んで「線」（放物線）を描けちゃうんだ。
今日はいっしょに、
y=1/2x^2
の二次関数のグラフをかいていこうか。
書き方1. 「点データの作成」
xとy データの「表」をつくるよ！
紙と鉛筆の用意はできたかな？
さっそく始めるよ！
まず、xの値の範囲を決めよう。
沢山あったほうがより正確なグラフがかける。
だけど、今はおおよその形がわかればいいから、
データは10程度あればいいかな。
ってことで、今回はxの変域を「-5 ≦ x ≦ 5」と範囲を決めよう。
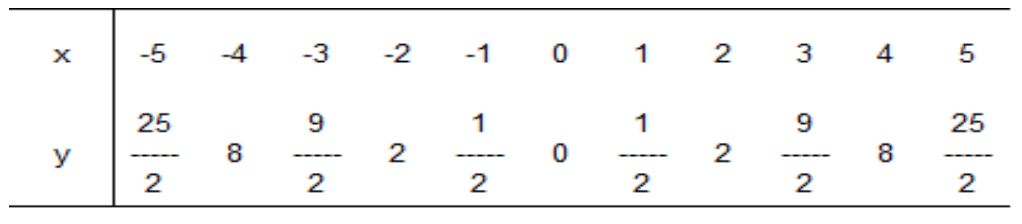
そうすると、表はこんな感じになる。
つぎはxの値をいれたときのyを求めればいいね。
地道に計算してみると、こうなる↓↓
- x=-5のとき、y=1/2 × ( -5) × ( -5 ) = 2分の25
- x=-4のとき、y=1/2 × ( -4 ) × ( -4 ) = 8
- x=-3のとき、y=1/2 × ( -3) × ( -3 ) = 2分の9
- x=-2のとき、y=1/2 × ( -2) × ( -2 ) = 2
- x=-1のとき、y=1/2 × ( -1) × ( -1 ) = 2分の1
- x= 0のとき、y=1/2 × 0 × 0 = 0
- x=1のとき、y=1/2 × 1 × 1 = 2分の1
- x=2のとき、y=1/2 × 2 × 2 = 2
- x=3のとき、y=1/2 × 3 × 3 = 2分の9
- x=4のとき、y=1/2 × 4 × 4 = 8
- x=5のとき、y=1/2 × 5 × 5 = 2分の25
計算ばっかでやんなっちゃうけど、ここは我慢しようね。
あとは計算結果を表にうめるだけ。
できたー？
書き方2. 「座標に点をうつ」
さっきの点データを座標にかきこんでいくよ。
今回グラフをかくのは、メモリの単位が1のの座標でかくんだ。
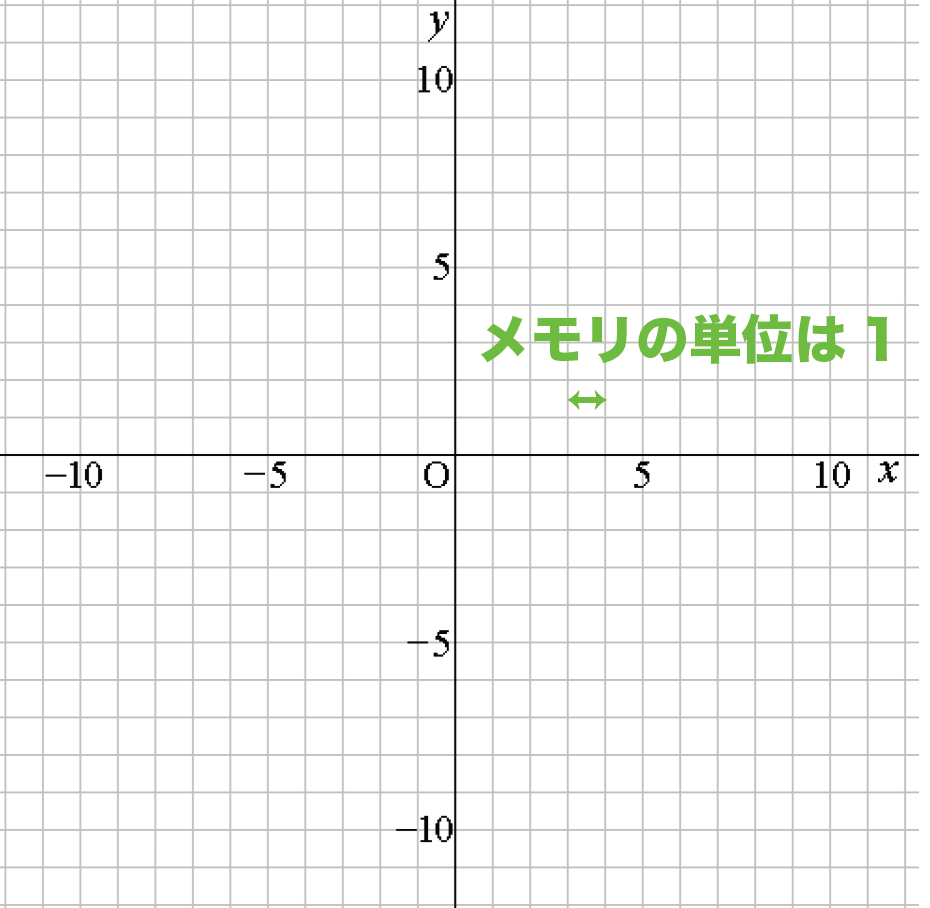
だから、座標の点はxとyが整数の点だけでいいね。
y=1/2x^2の点データでいうと、
- (-4, 8)
- (-2, 2)
- (0, 0)
- (2, 2)
- (4, 8)
の5つの点だね。
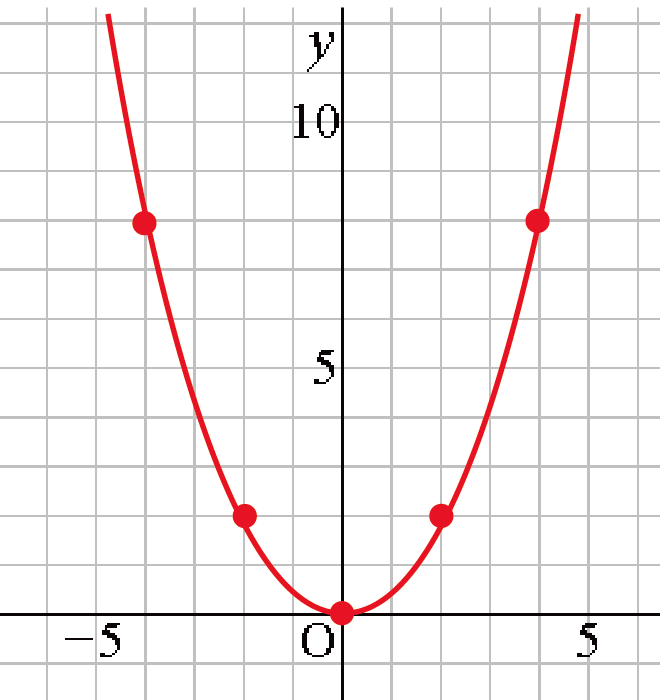
こいつを座標にうちこんでみると、
こうなるね。
書き方3. 「点と点をむすぶ」
最後に点と点を結んでいくよ！
フリーハンドでもいいし、ものさしを使ってもいいよ。
座標の点をもとに雰囲気と直感でかいていこう。
座標をうてないところは点データをもとに、
そこらへんを通るように調整しよう。
おーーーらっよっと、
全部頑張って描きあげたよ！
こんな感じになったかな？
まとめ：二次関数y=ax2のグラフの書き方は3ステップでイケル！
二次関数y=ax2の書き方はどうだったかな？？
きれいな二次関数の放物線のグラフをかくコツは、
たくさん点データを求めること。
これにつきるかな。
雰囲気の部分がすくなくなるからね。
あとは、いろんなグラフを描いてみよう。
またね(^_-)-☆
そら
