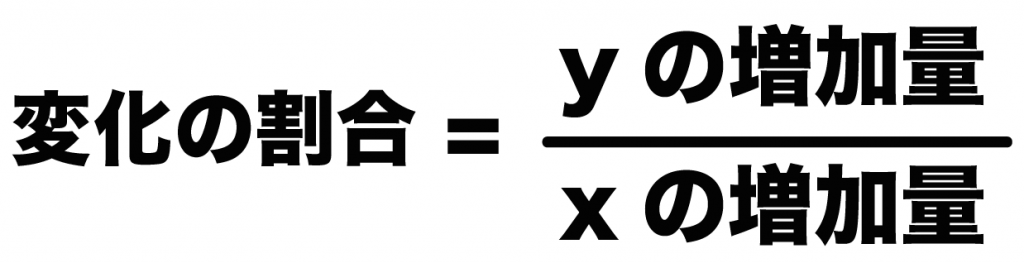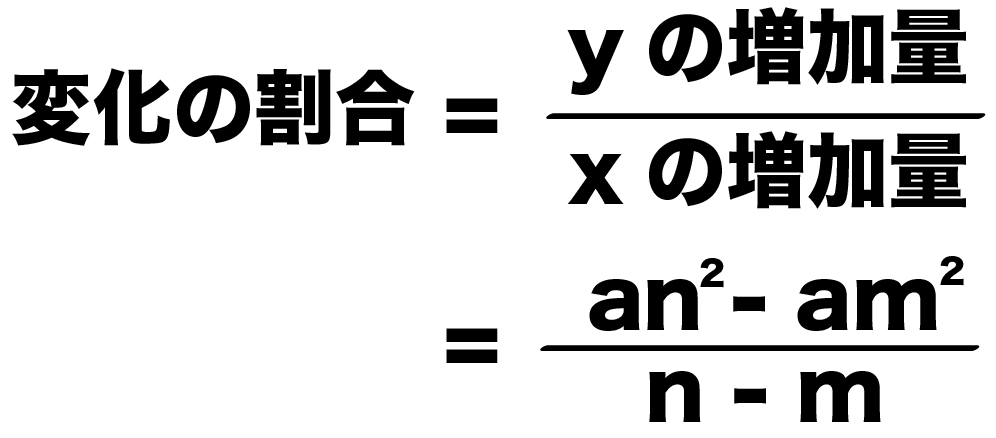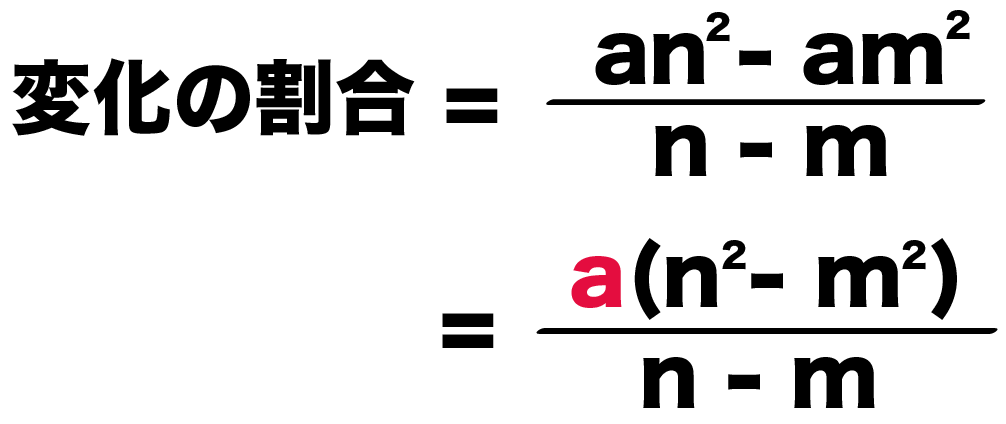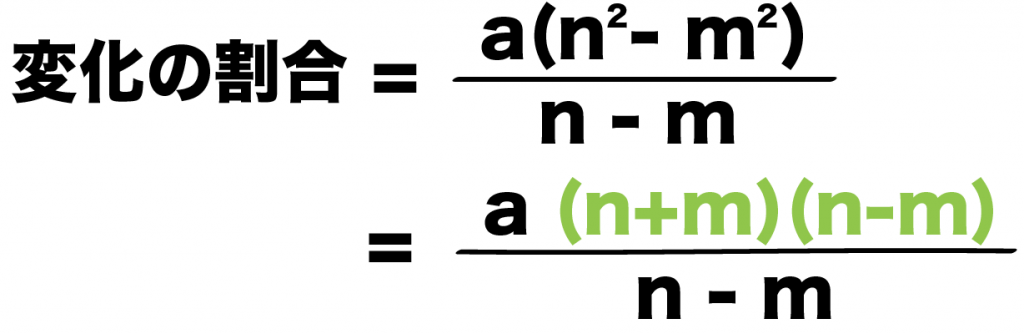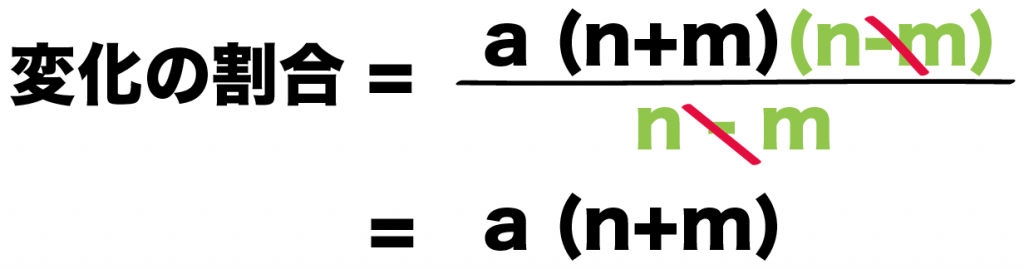二次関数y=ax2の変化の割合を3秒で計算できる公式
二次関数y=ax2の変化の割合の求め方に公式あるの??
こんにちは!この記事をかいてるKenだよ。服、ほしいね。
二次関数y=ax2の変化の割合の求め方には公式があるよ。
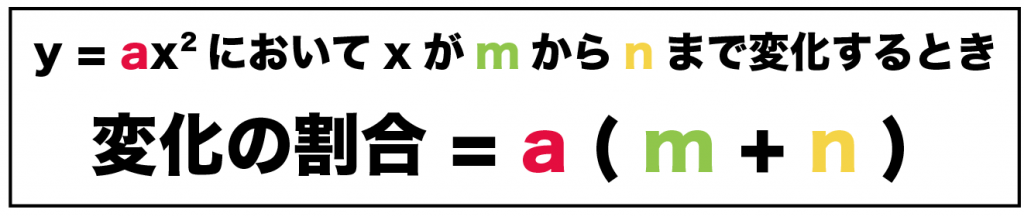
xの値がmからnまで増加するとき、変化の割合は、
a (m+n)
になるんだ。
つまり、
(比例定数)×(xの小さい値 + xの大きい値)
っていう計算。簡単だ!
さっそく、この公式で変化の割合を求めてみよう。
たとえば、
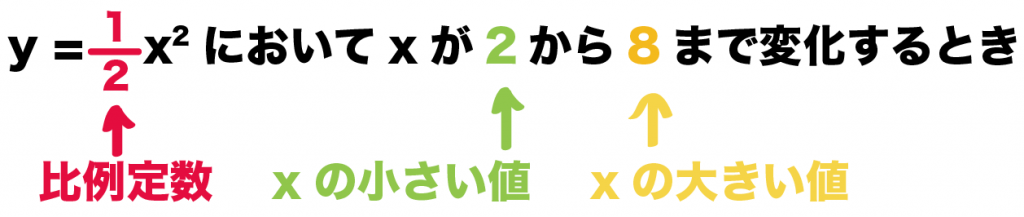
y=1/2x^2 でxが2から8まで増加するときの変化の割合を計算してみて。
この二次関数では、
- 比例定数a: 1/2
- xの小さいほうの端 m:2
- xの大きいほうの端 n:8
になってるね??
こいつをさっきの公式に代入してやると、
1/2 (2 + 8)
= 5
になるね。
つまり、
y=1/2x^2 でxが2から8まで増加するときの変化の割合は「5」になるわけ。
どう??簡単に計算できたよね??
なぜ、二次関数の変化の割合が公式で計算できるの??
二次関数の変化の割合の公式は便利。
どんな変化の割合の問題でもとけそうだ。
でもさ、
なんで変化の割合の公式がつかえちゃうんだろうね??
ちょっと便利すぎて怖い。
不安になってきたから、なぜ公式がつかえるのかを振り返ってみよう。
二次関数y=ax2がmからnまで変化するときを想定してみて。
このときの変化の割合を、二次関数の変化の割合の求め方で計算すればいいんだ。
- yの値を計算する
- 変化の割合を計算する
- 因数分解する
- 約分する
Step1. yの値を計算する
まずyの値を計算してみよう。
- xの小さい値 : m
- xの大きい値 : n
のときに、yの座標がいくつになるのか??
を求めればいいのさ。
それぞれのx座標をy = ax2に代入すればいいね。
y = ax2にmとnを代入してyを求めてやると、
- x = m のときy = am^2
- x = n のときy = an^2
になる。
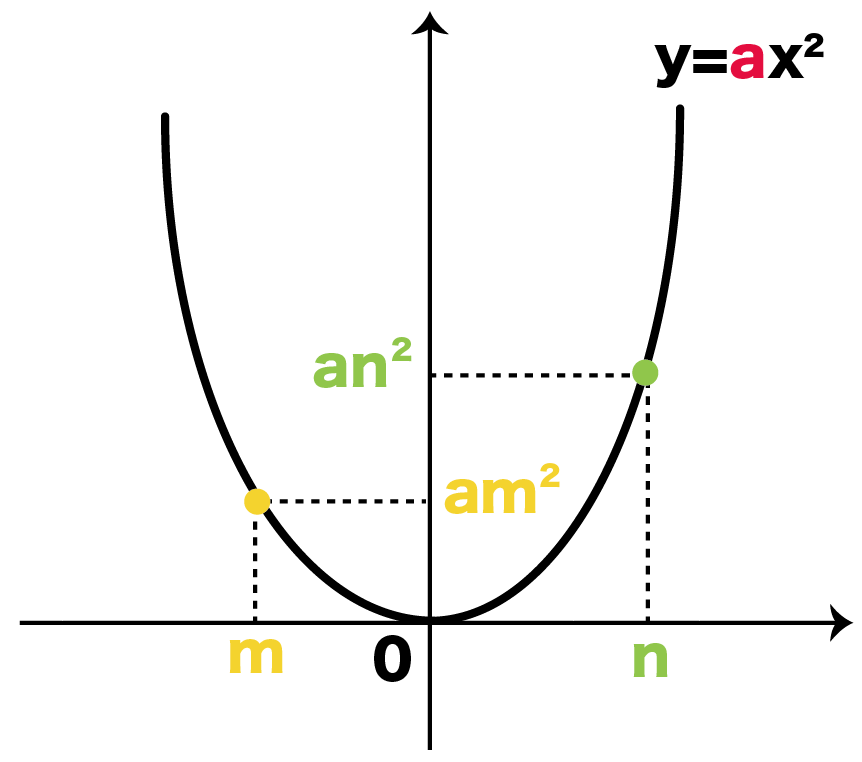
Step2. 変化の割合を計算する
つぎは変化の割合の求め方で計算してみよう。
(yの増加量)÷(xの増加量)
ようは、
xが1変化するごとにyはいくつ変化するのか??
ってことを調べるわけだ。
この計算式をつかうと、
変化の割合
= (yの増加量)÷(xの増加量)
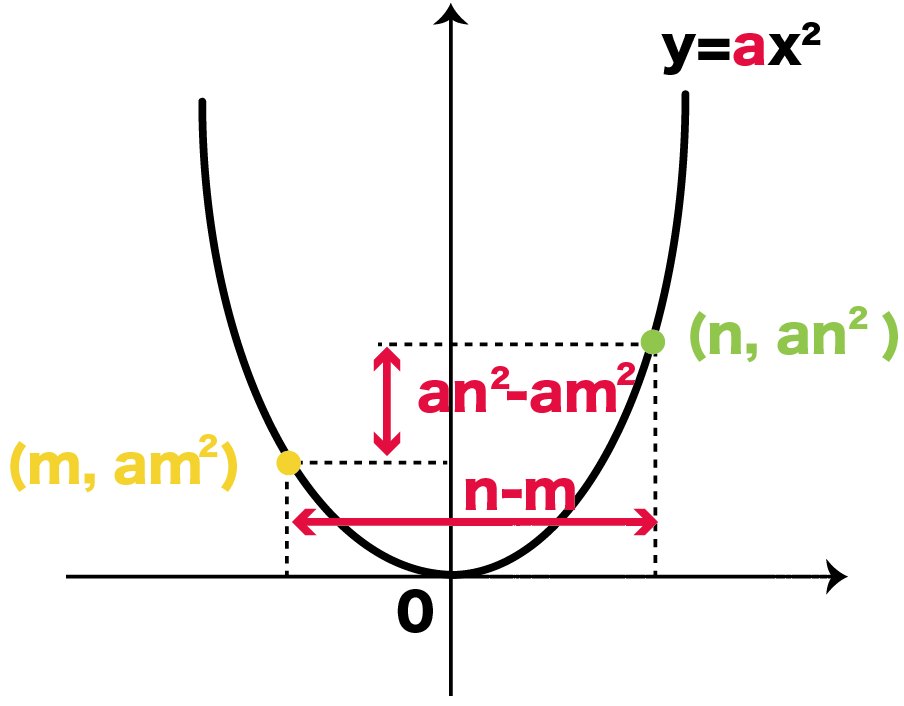
= (an^2 – am^2)÷(n – m)
になるね。
Step3. 因数分解する
さっきの変化の割合を因数分解してみよう。
分子の、
an^2 – am^2
がむちゃくちゃ因数分解できそうだ。
まず共通因数aでくくってやると、
a(n^2 – m^2)
になるね。
んで、さらに、()のなかの、
n^2 – m^2
を因数分解の公式で計算すると、
n^2 – m^2
= (n+m) (n-m)
になるじゃんね。
Step4. 約分する
最後に約分してあげよう。
変化の割合の分子と分母に共通の、
n – m
っていう因数があるよね??
そこで、
(n – m)で分子・分母を割ってやると、
a(n+m) (n-m) ÷ (n-m)
= a (n+m)
になるんだ。
xが増加する(または減少する)ときの話をしているから、
n と mが一緒であることはありえないはず。
つまり、
n≠m
だから、n-m≠0。
よって、n-mでわってもいいから大丈夫だ。
あ。
こ、これはいちばん最初に紹介した、
変化の割合 = a (m+n)
っていう公式になってるね。
こんなかんじで、変化の割合の求め方で計算すれば公式が導けるのさ。
やったね。
まとめ:二次関数y=ax2の変化の割合の公式は便利すぎて注意
二次関数y=ax2の変化の割合は公式なら簡単。
すぐに変化の割合をだせるね。
便利な公式をおぼえるのも大事だけど、
なぜ、公式がつかえるのか?
ってこともおなじぐらい重要。
公式がつかえる理由をわかってから公式をつかおうね。
そんじゃねー
Ken