二次関数の利用の文章問題が苦手！
ある日、数学が苦手なかなちゃんは、
二次関数の利用の文章題に逆ギレしていました。
あー、もうやだ！！
なんで二次関数y=ax2でも、
文章問題でてくんだよ！？
あー、なるほどね、
うわあっ！？
先生か、びっくりした……
せっかく二次関数y=ax2に慣れてきたのに……
式が立てられないから、
解けないのかな？
！？
なんでわかるの？
先生って超能力者？
そういう人、結構いるよ。
1年、2年でも関数の文章題出てきたけどね
わたし苦手だった！
そんな文章題アレルギーっ子への朗報！
へっ？何？？
えっ、そうなの？
そう！
基本のパターンを理解すれば……
じゃあ、二次関数の文章題を攻略しよう！
あれっ？
すごくやる気だね……
てへ！
二次関数の利用の3つの文章問題
二次関数の利用の文章問題には3パターンあるよ。
- 表から式をよみとる
- 二次関数の式に代入する
- 変化の割合と変域をよみとる
3つもあるんだ！
おもいやられるわ。
どれもわかりやすいから大丈夫！
順番にみていこう。
はい！！
文章題1. 「表から式を読み取る」
1つめの文章題は、
xとyの表から式をよみとるだけ！
へ？
読み取るだけ？？
そう！
たとえば、つぎのような問題ね。
練習問題1.
ボールが天から落ちています。
落下し始めてからの時間をx秒、
その間に落下する距離をymとします。
xとyの関係は以下の表の通りです。
このとき、
xとyの関係を式であらわしなさい。
ｘが1増えると、yが5増えて、
ｘが2増えるとyが20増え……
比例と全然違う！！
実は、これも比例なんだけどね。
じゃあ、1倍、2倍って考えてみよう。
ｘが2倍になると、yは4倍で、
ｘが3倍になると、yは9倍で……
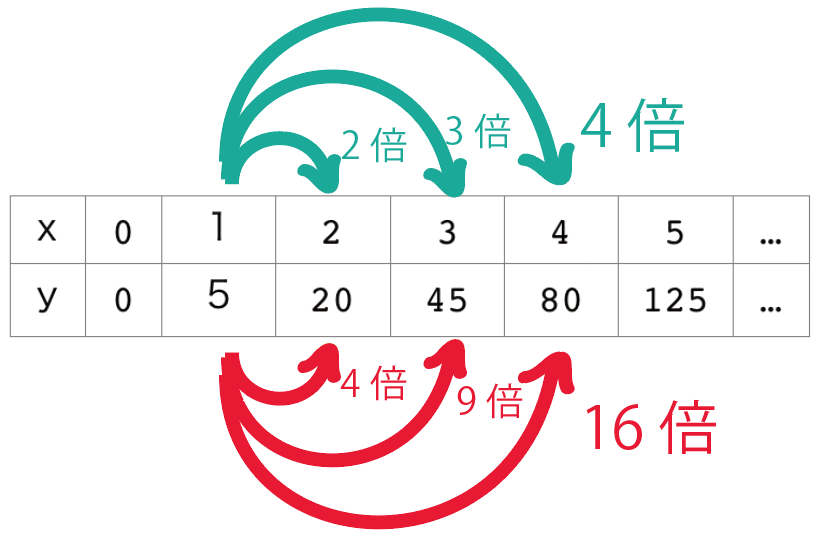
4，9，16って聞いて何か気付くことは？
あっ、何かの2乗になってる！！
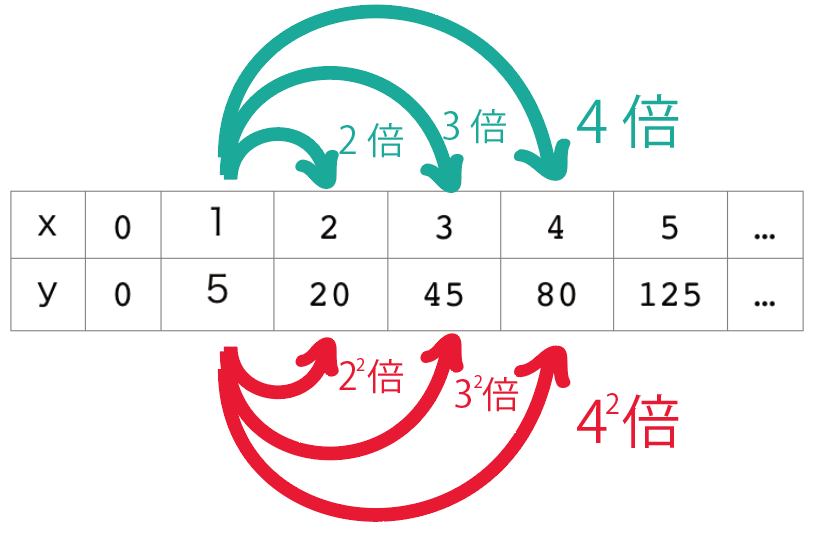
こんな関係のときに使うのが、
y=ax²！
なるほど！
この表の関数の式はどうなるかな？
xとyを「y=ax2」に代入すればよかったよね？
お、いいんじゃない？
x=1、y=5を代入して……
5=aになるから、y=5x²！
そう！
これで一つ問題が解けるようになった！
にやり
文章題2. 「式に代入する」
2つめの文章問題は、
二次関数y=ax2に代入するやつ。
代入かああ・・・
そうそう！
むずくないから大丈夫！
たとえば、つぎのような文章題だよ。
練習問題2.
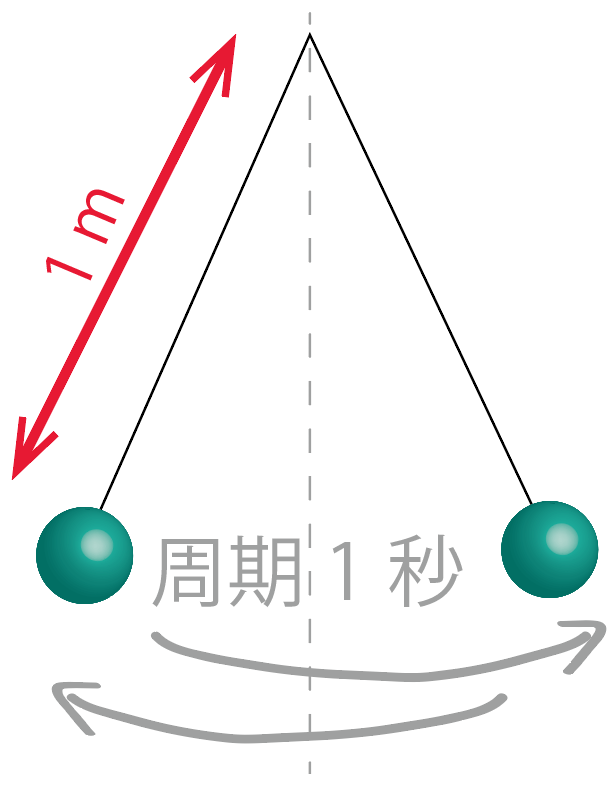
振り子があります。
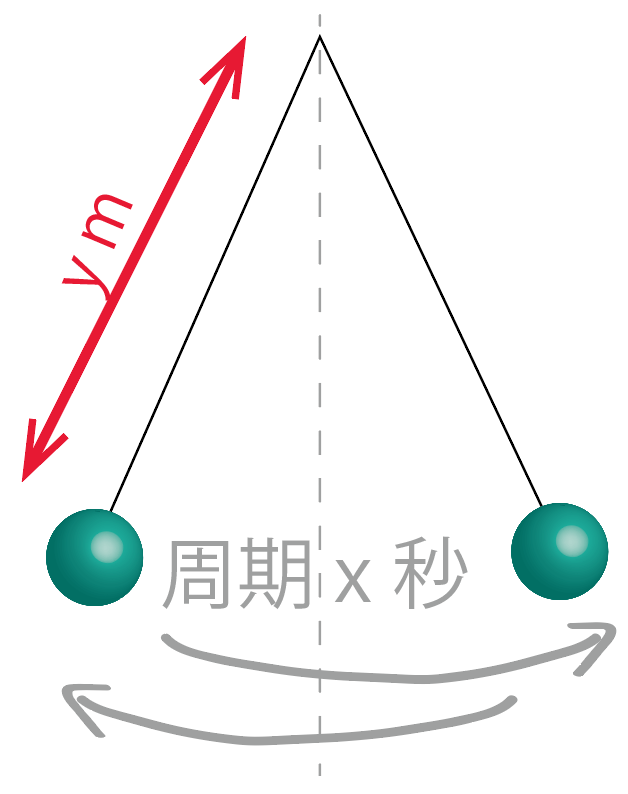
周期がx秒の振り子の長さをymとすると、
y=x²っていう関係になります。
周期が1秒の振り子の長さは何mでしょう？
振り子ってなんだっけ？？
よく漫画ででてくるよ。
ワンピースでいうと、
ジャンゴ。
ポケモンでいうと、
スリーパーがもってるやつよ。
あ、あれか！
そこで、問題！
周期が1秒の振り子の長さは何mでしょう？
式に代入しちゃえばいいんだ！
周期はxだから、x=1を代入しよう。
y=x^2
= 1^2 = 1
になる！
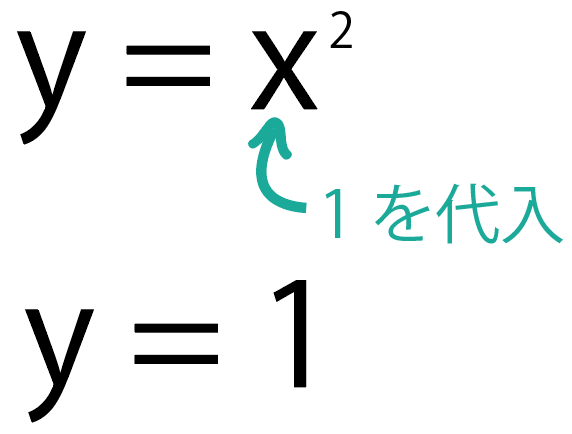
そう！だから、
振り子の長さ は1 m
になるよ！
いぇーい
文章題3. 「変化の割合を求める」
二次関数y=ax2の変化の割合
をもとめる問題。
なんか、難しそう。
そんなことないよ！
たとえば、こんな問題！
練習問題3.
ボールが72mの坂を転がり始めてからの時間をx秒、
その間に転がる距離をymとします。
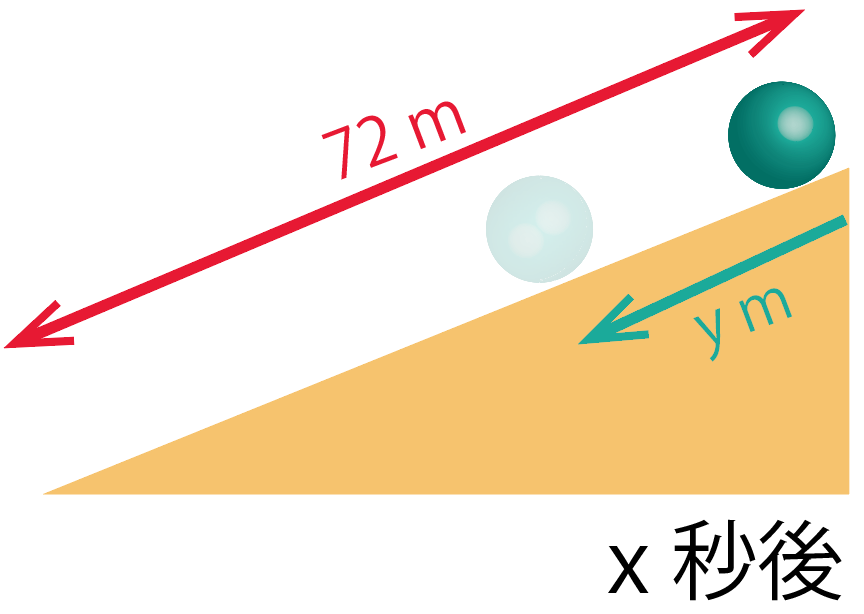
なんと、xとyには、
y=2x²という関係がありました。
このとき、1秒後から3秒後までの平均の速さを求めなさい。
また、xの変域もだしてね。
うわぁ、なんか、
文章題っぽい文章題でイヤだ。
でも、見て！
2次関数の式が問題に書いてある！
あっ、y=2x²のことかな？
そう。
もう一つ注目してほしいのは、
【平均の速さ】
どう注目すればいいの？
平均の速さは、
【変化の割合】と同じ意味を持っている！
え！なんで？！
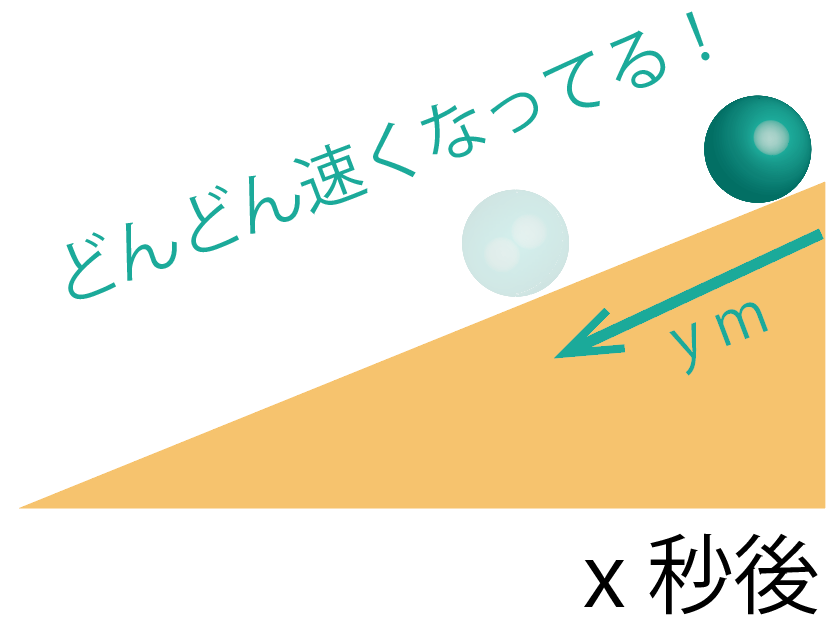
じつは、このボール。
瞬間ごとにどんどん速さが速くなってるのよ。
だから、どっからどこまでの速さ
っていう平均の速さとらないと、
速さを特定できないわけよ。
なるほど・・・
まあようは、
二次関数の変化の割合
を求めればいいってことね。
そう！
解き方もおなじ！
おしい！
答え8だと、○がつかない！！
速さだから、
秒速8ｍだ！！
あ、
あと変域がのこってた
文章題の大切なポイント！
【実際にあり得る範囲が変域になる】
この問題だと、坂が72mしかないから、
この2次関数はy=72までしかない。
じゃあ、yの最小値はどこだろう？
０が一番小さいって覚えておくといいよ！
たしかに。
－1mとか、－2mって想像できない
じゃあ、yの変域は、0≦y≦72になるね。
xの変域を求めてみよう！
代入しちゃえばいいやつだ！
y=0のとき、x=0。
y=72のとき、
72=2x²
36=x²
x= ±6
ってあれ？
マイナスも出てきた！
そう！
でも、マイナスはあり得ないよね？
だって、秒数だもんん。
だから、
y=72のとき、x=6ってこと。
0≦x≦6だ！
そう、正解！
まとめ：二次関数y=ax2の利用って簡単じゃん！
二次関数の利用って簡単かも！！
って思ってもらうのが、
今回の目的！
中学の二次関数はy=ax²しか出てこない。
基本のパターンが少ないんだ！
- 表から式を読み取る
- 式に代入する
- 変化の割合と変域を求める
うんうん
レッツチャレンジ！
