【計算公式】正四角錐の体積の求め方がわかる3ステップ
正四角錐の体積の求め方の公式って??
こんにちは!この記事をかいているKenだよ。青い空が好きだね。
正四角錐の体積の求め方には公式があるんだ。
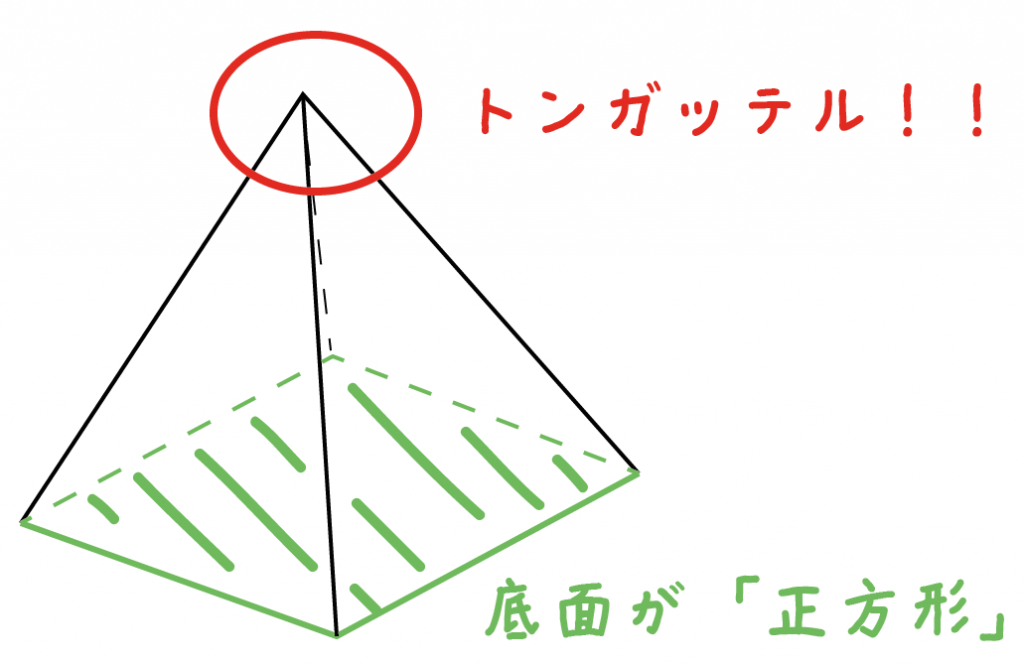
正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。
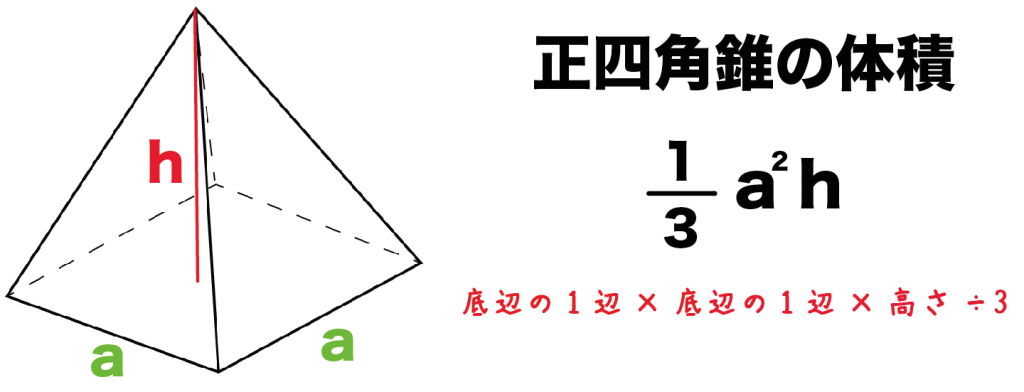
底面の1辺の長さをa、高さをhとすると、体積はつぎのようにあらわせるよ。
1/3 a²h
つまり、
(底辺の1辺)×(底辺の1辺)×(正四角錐の高さ)÷3
ってことだね。
今日は、この計算公式をどうやって使うのか??
ということをわかりやすく解説していくよ。
正四角錐の体積の求め方がわかる3つのステップ
正四角錐の体積は3つのステップで計算できちゃうんだ。
例題をときながらみていこう!
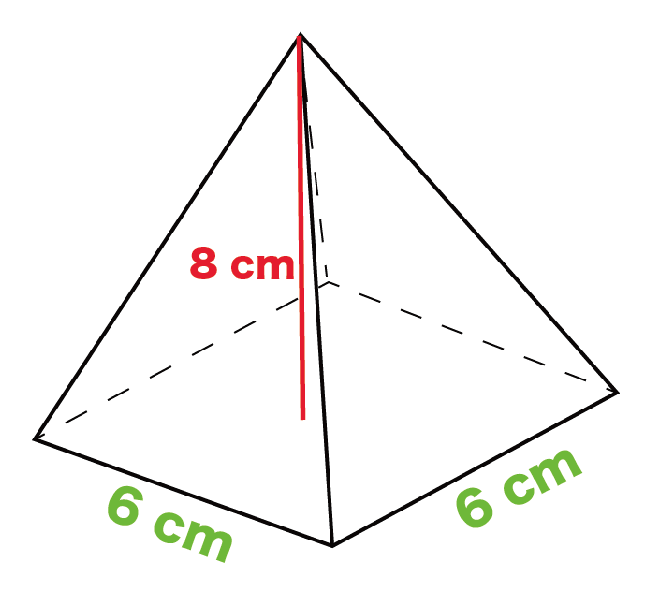
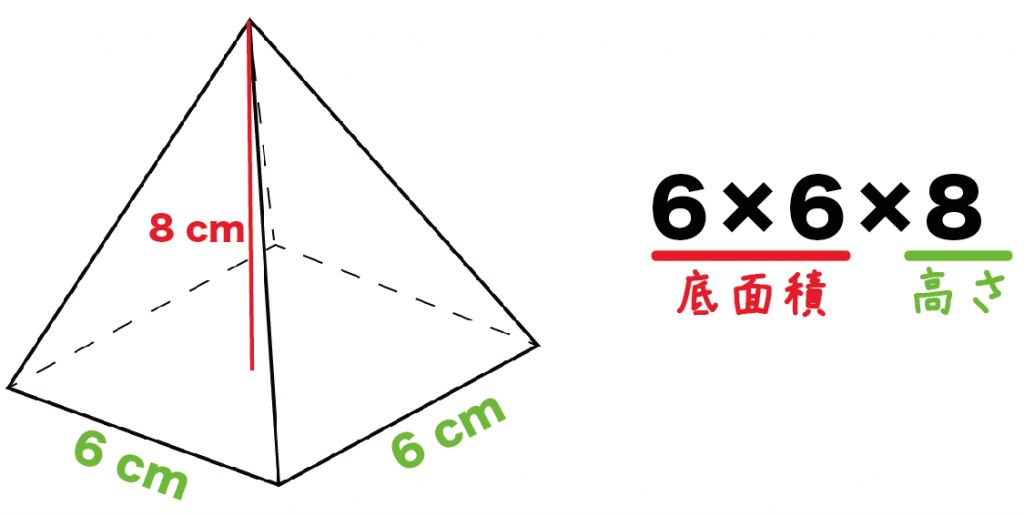
底辺の1辺の長さが6 [cm]、高さが8 [cm]の正四角錐の体積を求めてください。
Step1. 底面積を計算するっ!
まずは正四角錐の底面積を求めてみよう。
正四角錐の底面は「正方形」だよね?? 正方形の面積を「1辺×1辺」という公式をつかって計算してくれ。

例題でいうと、
底面の正方形の1辺は6[cm]だよね。だから、底面積は、
6×6 = 36[cm²]
になる。
Step2. 正四角錐の高さをかけるっ!
さっき計算した底面積に「高さ」をかけてみよう!
例題の正四角錐の高さは8 [cm]だから、
36×8
= 288[cm³]
になるね。
計算ミスに気をつけてね。
Step3. 最後に1/3をかける
底面積に高さもかけたし・・・
と安心してはダメ。
先がとんがっているタイプの「錐体」では、体積を求めるときに必ず「1/3」をかけなきゃいけないんだ。
えっ。なぜ1/3をかけるのかって??
それは円錐の体積の求め方でも触れたけど、
高校数学でならう「積分」を使わないと説明できないんだ。
だから、中学数学ではとりあえず、
先がとんがっている立体の体積の計算は「底面積×高さ×1/3」になる
って覚えておけば問題ないよ。
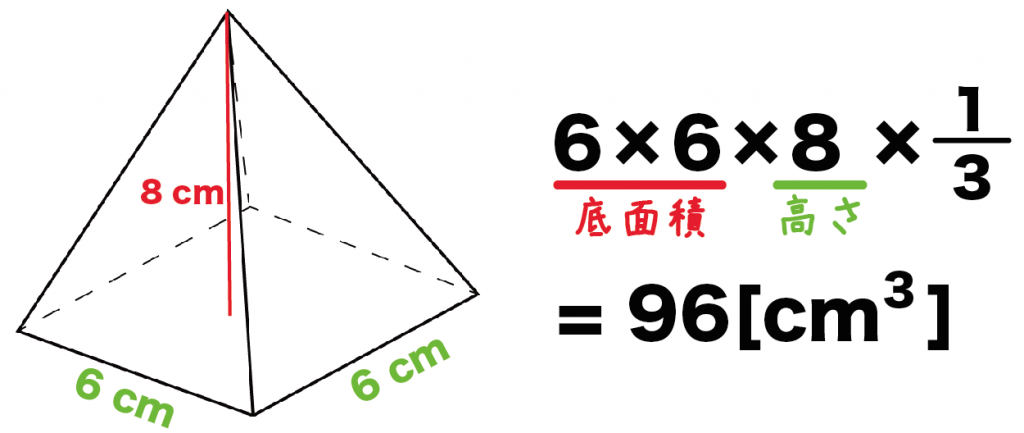
だから例題の正四角錐の体積は、
6×6×8×1/3
= 96[cm³]
になるんだ。
おめでとう!これで正四角錐の体積を計算できたね。
まとめ:正四角錐の体積の求め方も大丈夫!
正四角錐の体積の公式はどうだった??
底面積×高さ×1/3
という計算をゆっくりしてみてね。テスト前に復習しておくと心強いかも!
そんじゃねー
Ken