多角形の内角の和の公式ってあるの？？
こんにちは！この記事をかいているKenだよ。パイプユニッシュ、ほしいね。
多角形の内角の和の公式ってめちゃ便利。
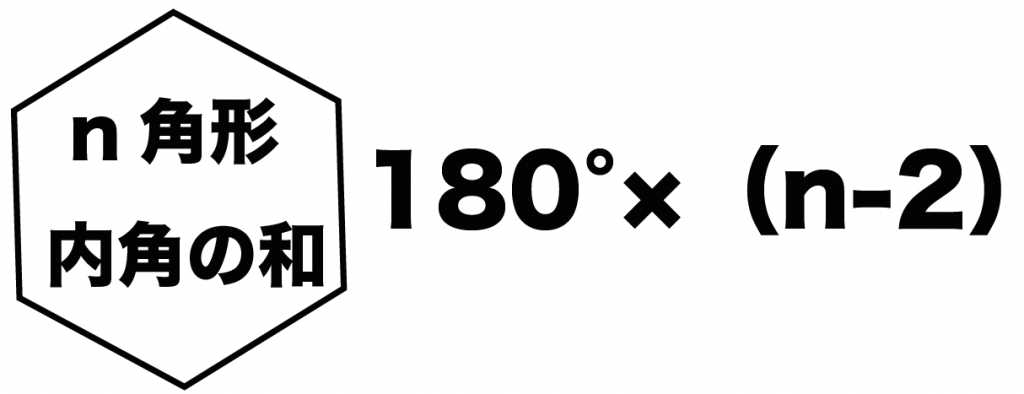
n角形の内角の和を求めたいときは、
180°× (n -2)
で計算できちゃうのさ。
たとえば、
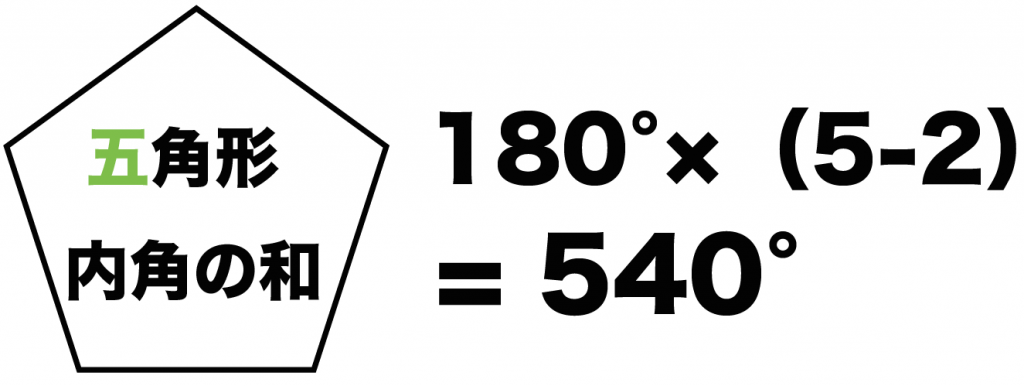
五角形の内角の和を計算したいときは、
nに「5」を代入すればいいんだ。
180°×（5-2）
= 540°
になるね。
つまり、
五角形の内角をぜーんぶたしたら540°になるってわけさ。
なぜ多角形の内角の和が公式で計算できるの？？
多角形の内角の和の公式
180°×（n-2）
では、
- 180°＝「三角形の内角の和」
- (n-2)＝「多角形にふくまれる三角形の数」
をあらわしているよ。
三角形の内角の和は「180°」ってならったから、
多角形の中に何個の三角形がひそんでいるか？？
をあばいてやればいいってわけさ。
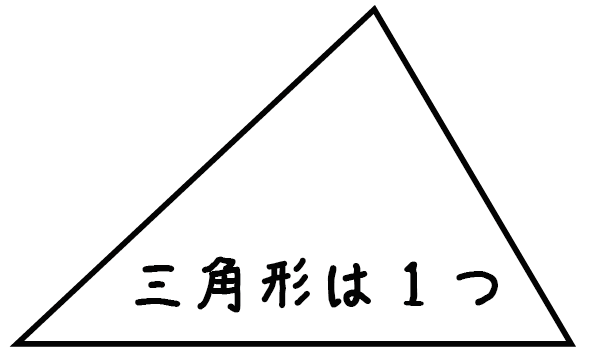
三角形の中には三角形が・・・1つ！
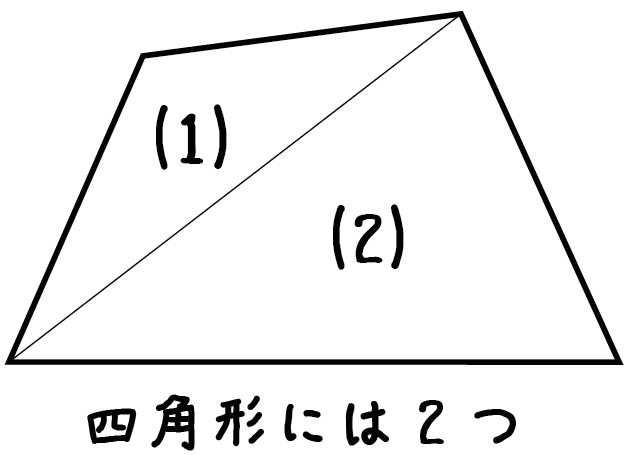
四角形の中には三角形が・・・2つ！
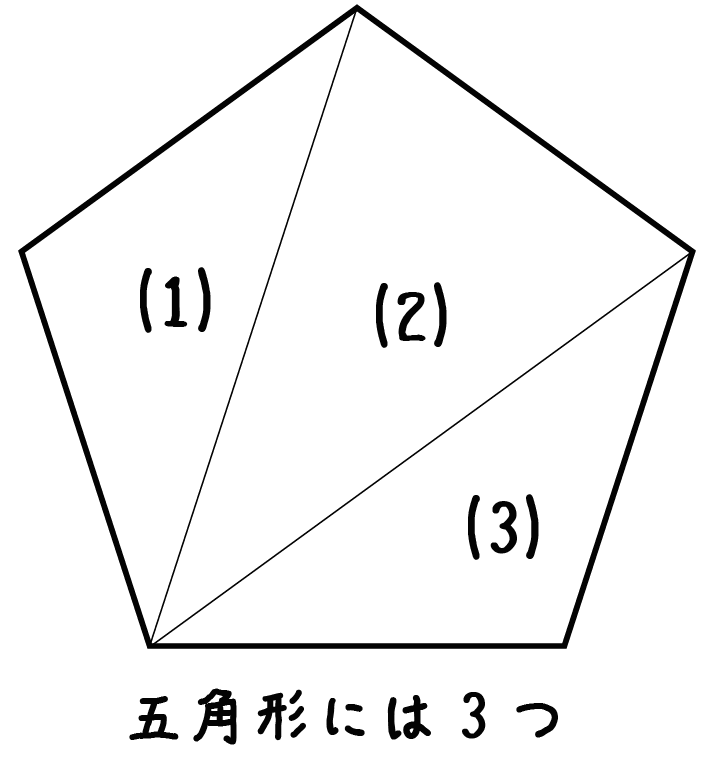
五角形の中には三角形が・・・3つ！
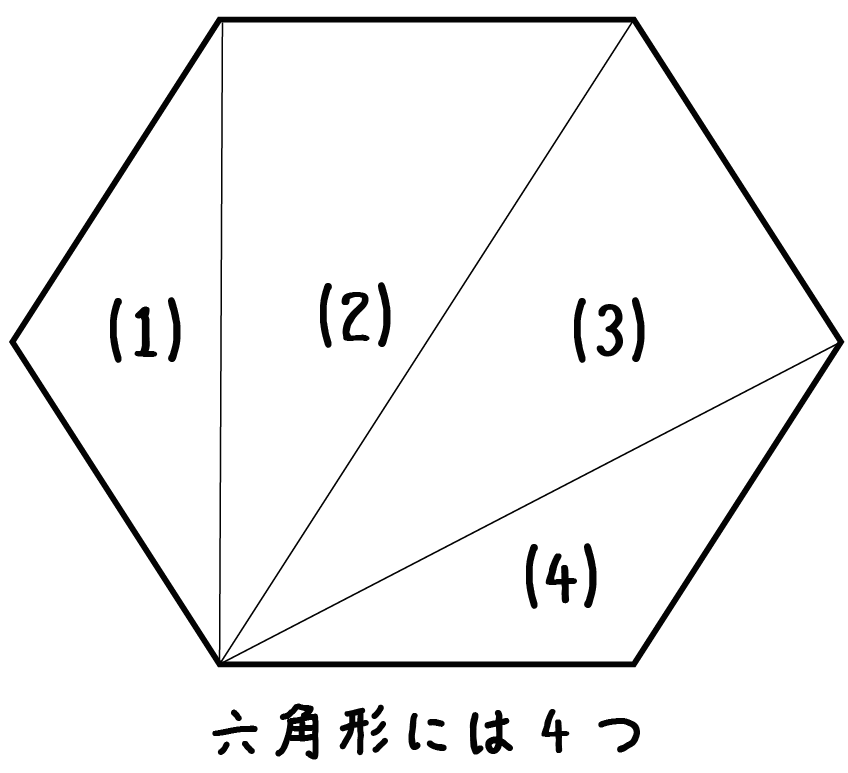
六角形の中には三角形が・・・4つ！！
七・・・・
ふう。
六角形まで確かめてみて「あること」に気づかない？？
そう、じつは、
多角形には「角の数 -2」個の三角形がひそんでいるんだ。
「五角形」だったら、
「5」から「2」をひいた「3」個の三角形がかくされているというわけさ。
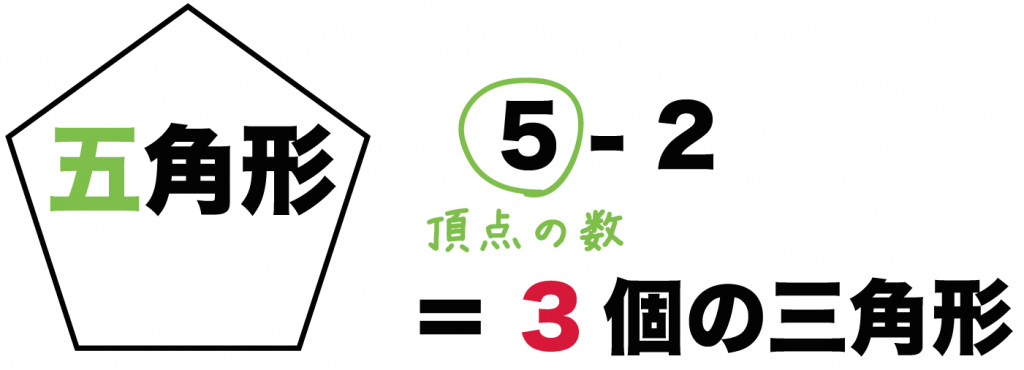
n角形のときは（n-2）個の三角形がかくれているというわけさ。
三角形の内角の和は180°だから、
(n-2)個の三角形がかくれている多角形の内角の和は、
180°× (n-2)
になるのさ。
だから、五角形の内角の和は、
180°×（5-2）
= 540°
になるんだね。
まとめ：多角形の内角の和は三角形の数できまる！
n角形の内角の和は、
180°×（n-2）
で計算できちゃうんだ。
内角の和をじゃんじゃん求めてみよう！
そんじゃねー
Ken
