平行線と線分の比の問題の解き方がわかる3ステップ
平行線と線分の比の問題の解き方がわかる3ステップ
こんにちは!ぺーたーだよ。
相似の単元では、
相似条件とか、
相似の証明とか、いろいろ勉強してきたね。
今日は ちょっと新しい、
平行線と線分の比のから辺の長さを求める問題
について解説していくよ。
たとえば、つぎのような問題ね↓
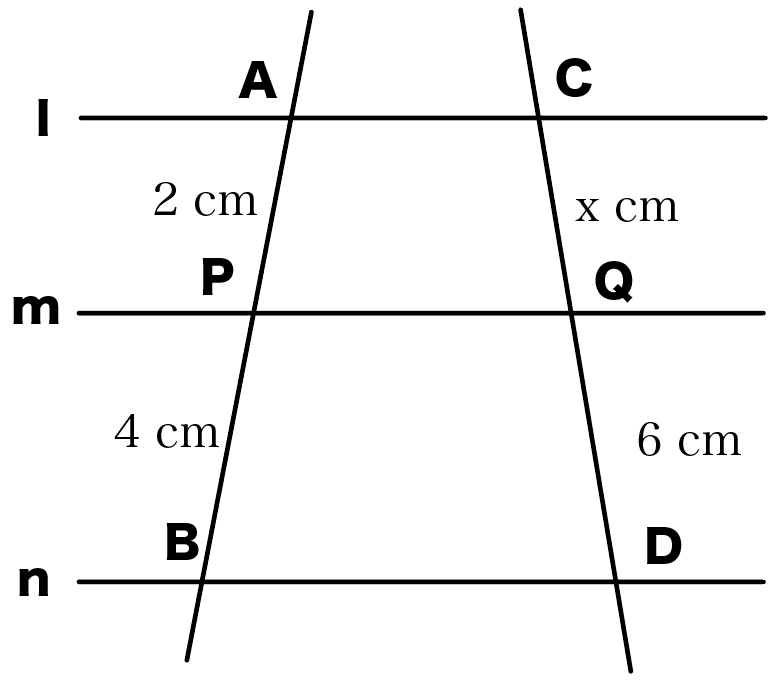
平行線とか線分がたくさんあって、ちょっと難しそうだね。
だけど、慣れちゃえば簡単。
「これはできるぜ!」っていうレベルになっておこう。
次の段階に分けて説明してくね。
目次
- 平行線と線分の比の性質
- 問題の解き方3ステップ
- 問題演習
平行線と線分の比の性質ってなんだっけ??
問題をとく前に、
平行線と線分の比の性質を思い出そう。
3つの平行な直線(l・m・n)
と
2つの直線が交わる場面をイメージしてね。
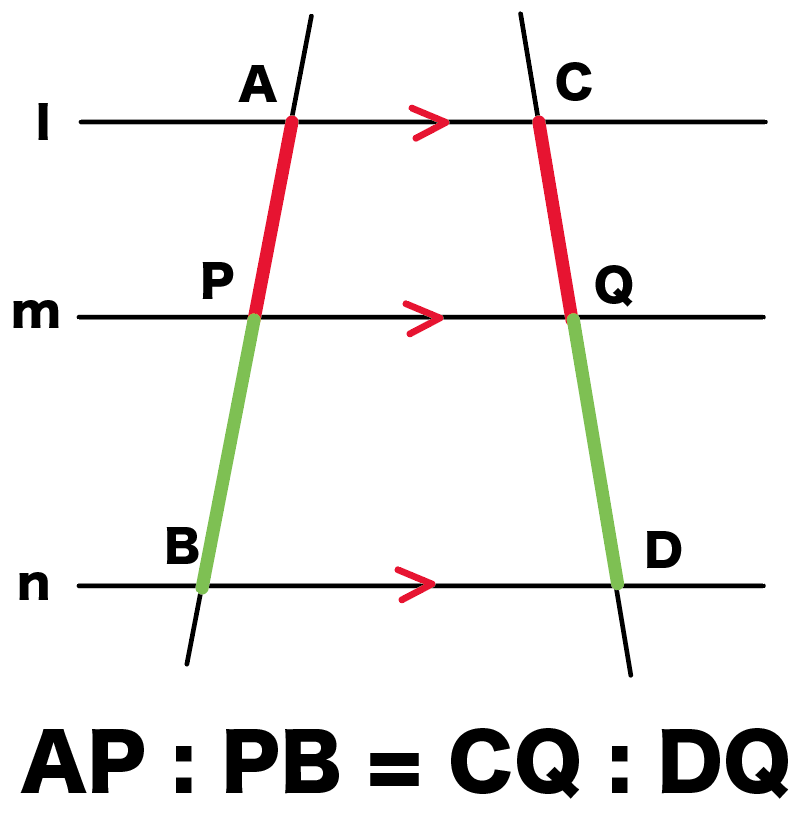
このとき、
AP:PB=CQ:QD
が成り立つんだ。
つまり、
平行線にはさまれた、
向かいあう線分の長さの比が等しい
ってわけね。
これさえおさえておけば大丈夫。
平行線と線分の比の問題もイチコロさ!
平行線と線分の比の問題の解き方3ステップ
さっそく、平行線と線分の比の問題を解いてみようか。

この手の問題は3ステップでとけちゃうよ。
- 対応する線分を見極める
- 比例式をつくる
- 比例式をとく
Step1. 対応する線分を見極める
平行線と線分の比がつかえる線分を見極めよう!
平行線にはさまれた線分のセット
をさがせばいいってわけね。
練習問題でいうと、
- AP
- PB
- CQ
- DQ
で平行線と線分の比がつかえそうだ。
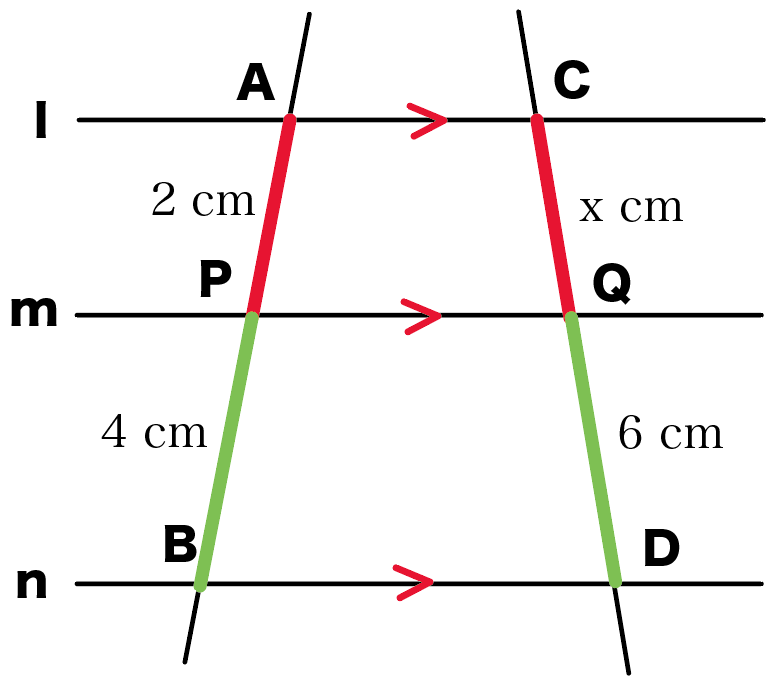
なぜなら、こいつらは、
3本の平行線(l・m・n)にはされまれてるからさ。
あきらかに3本の平行線に囲まれてる。
Step2. 比例式をつくる
平行線と線分の比の性質で比例式をつくってみよう。
平行線と線分の比の性質は、
2つの直線が、3つの平行な直線と交わるときAP:PB=CQ:QD
だったね??

だから、練習問題でいうと、
AP : PB = CQ : DQ
2 : 4 = x : 6
っていう比例式ができるはず!
Step3. 比例式をとく
つぎは、比例式をといてみよう。
練習問題でつくった比例式は、
2 : 4 = x : 6
だったよね??
比例式の解き方の「内項の積・外項の積」で解いてやると、
2 : 4 = x : 6
4x = 2×6
4x = 12
x = 3
になるね。
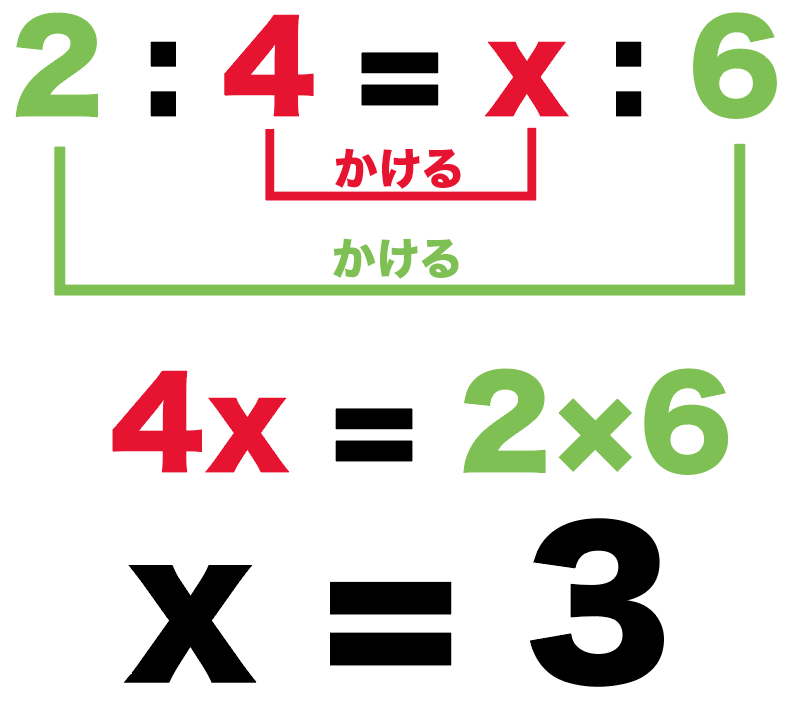
つまり、
求めたかったCQの長さは「3 cm」ってこと。
やったね!
平行線と線分の比に関する超実践的な2つの問題
平行線と線分の比の性質もだいたいわかったね。
あとは練習問題でなれてみよう。
今日はテストにでやすい問題を2つ用意したよ。
平行線と線分の比の問題になれてみようぜ。
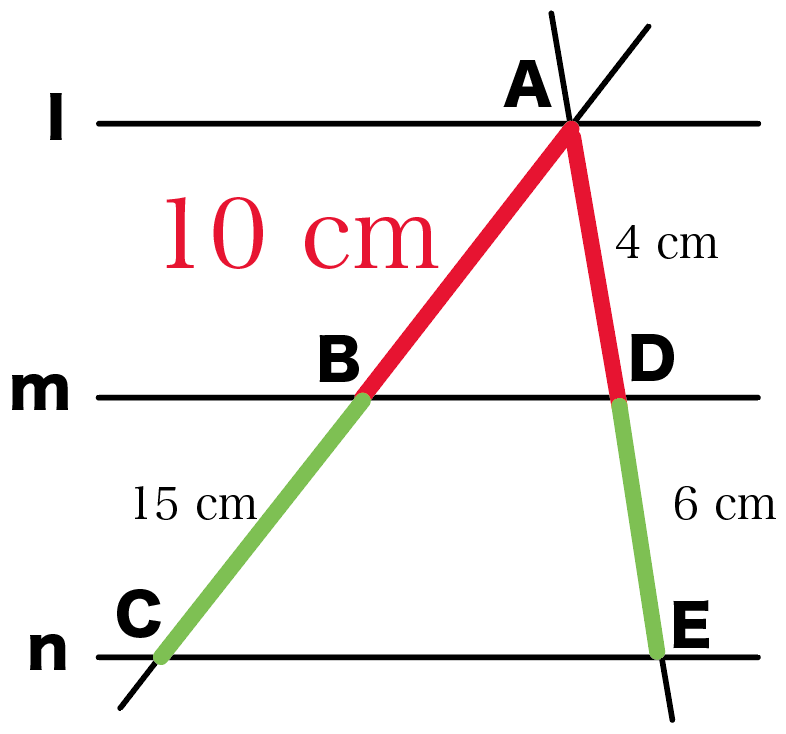
平行線と線分の比の問題1.
l//m// nのとき、xの大きさを求めなさい。
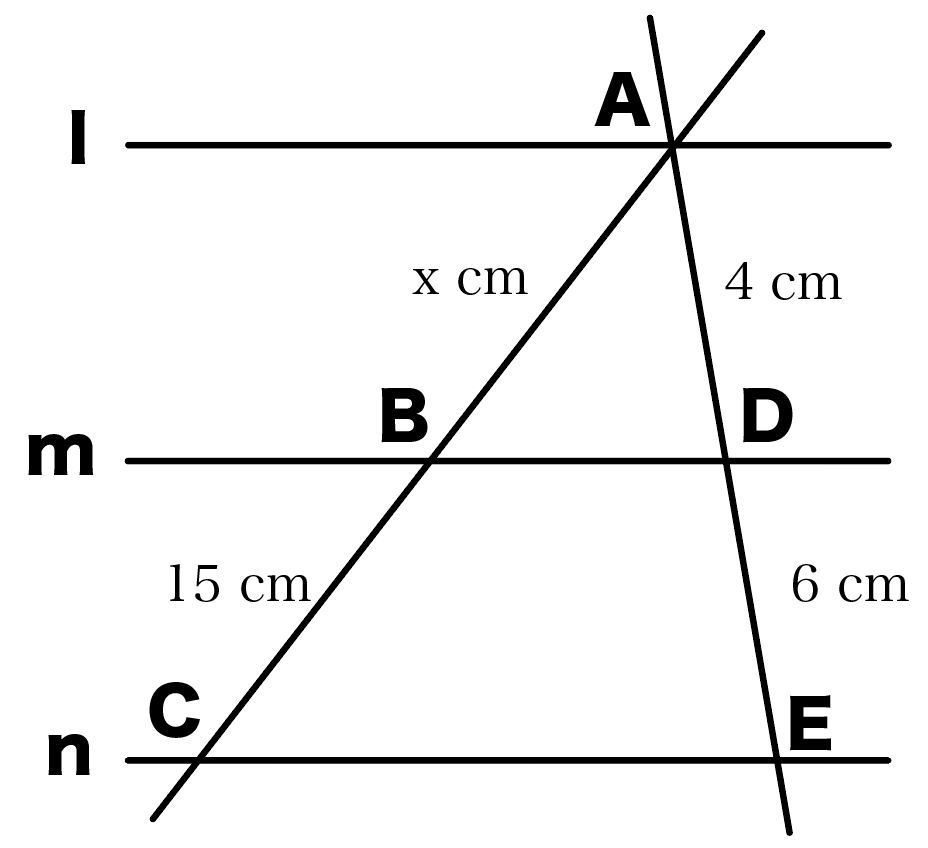
この手の問題は、
AB : BC = AD : DE
という平行線と線分の比をつかえば一発さ。
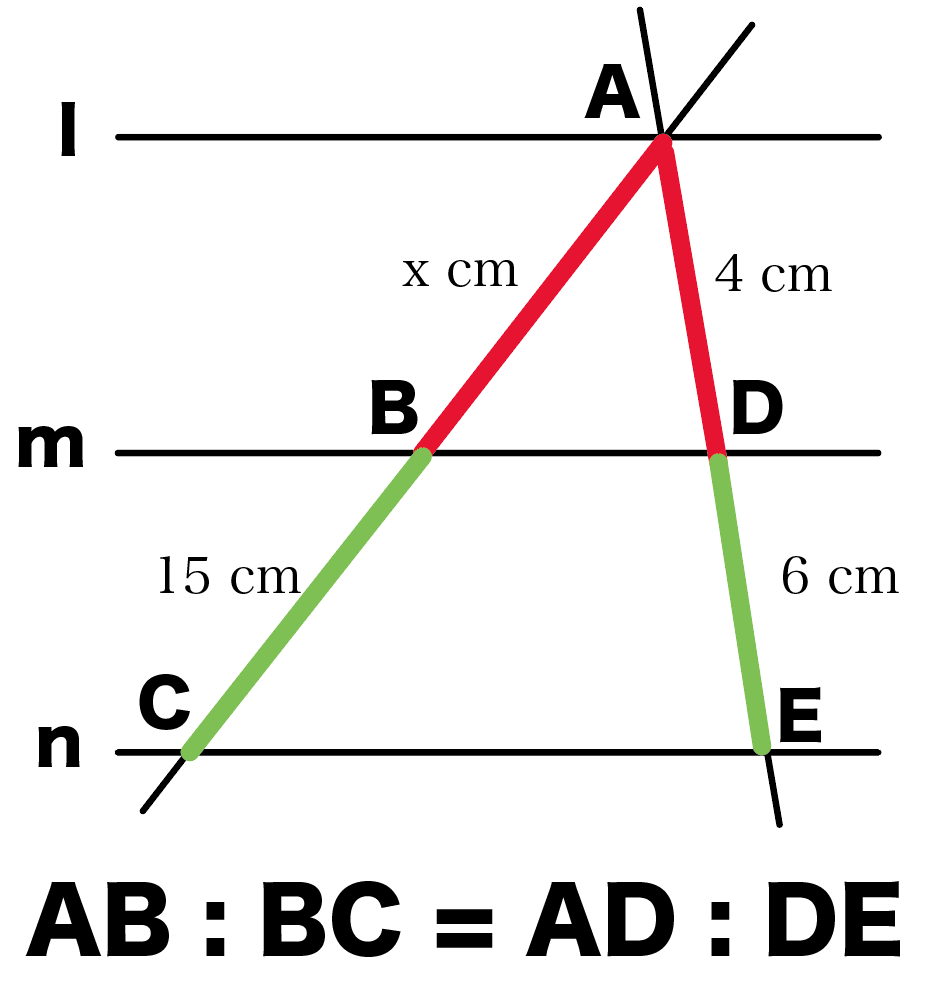
これは、△ABDと△ACEが相似だから、
対応する辺の比が等しいことをつかってるね。
えっ。
なんで相似なのかって??
それは、同位角が等しいから、
- 角ABD = 角ACE
- 角ADB = 角AEC
がいえるからなんだ。
三角形の相似条件の、
2組の角がそれぞれ等しい
がつかえるし。
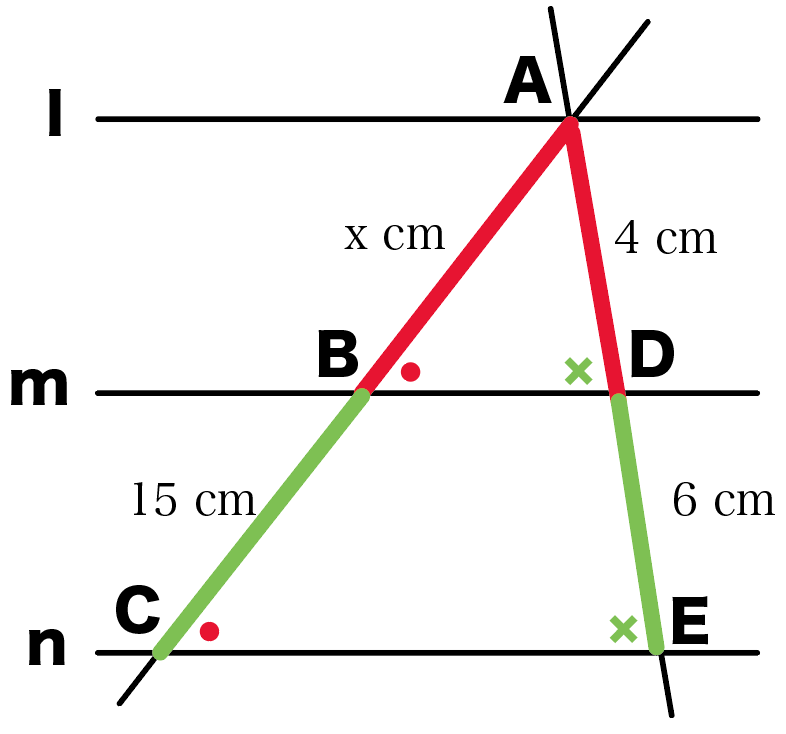
さっそく、この比例式をといてやると、
AB : BC = AD : DE
x : 15 = 4 : 6
x = 10
になるね。
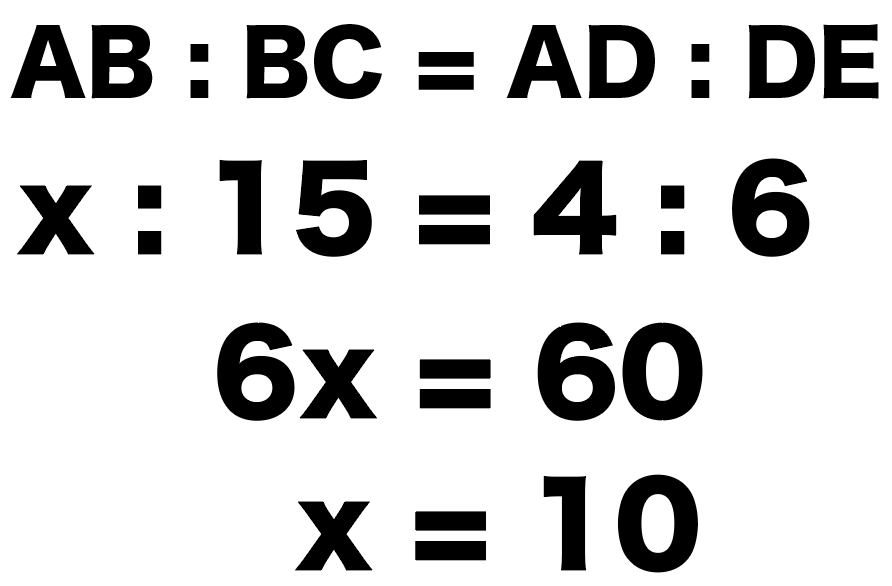
ってことは、ABの長さは、
10cm
になるってこと!
平行線と線分の比の問題2.
l//m// nのとき、xの大きさを求めなさい。
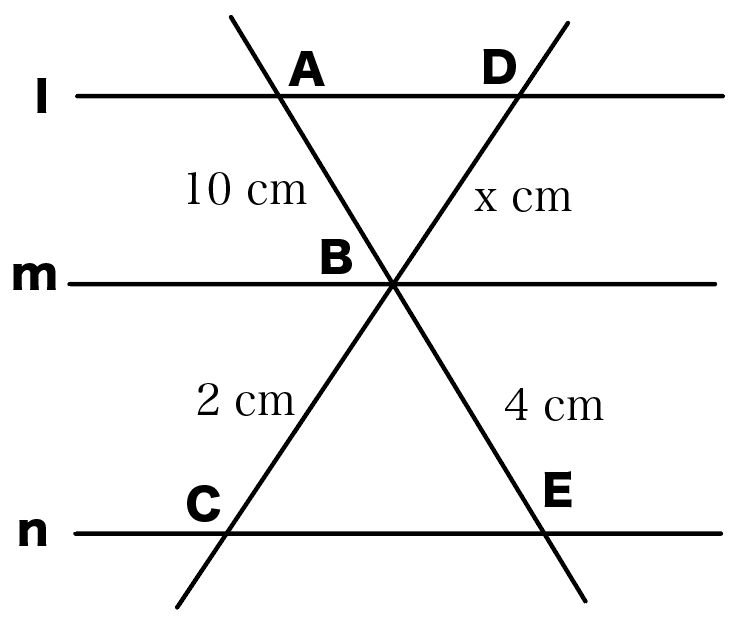
今度は直線がクロスしている問題だ。
対応する部分に色を付けるとこうなるよ。
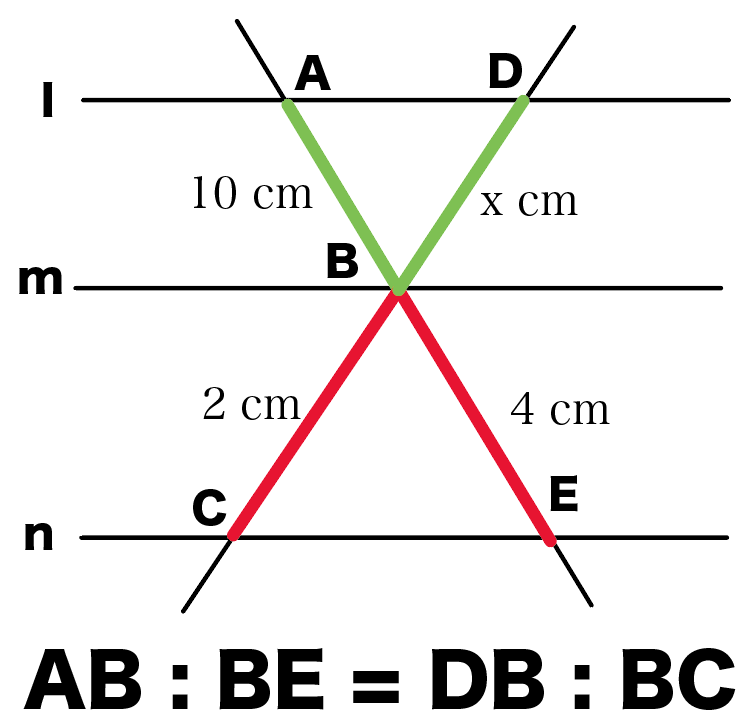
なぜなら、これもさっきと同じで、
△ABDと△EBCの相似をつかってるから使えるんだ。
l・m・nがぜーんぶ平行だから、
錯角が等しいことがつかえるね。
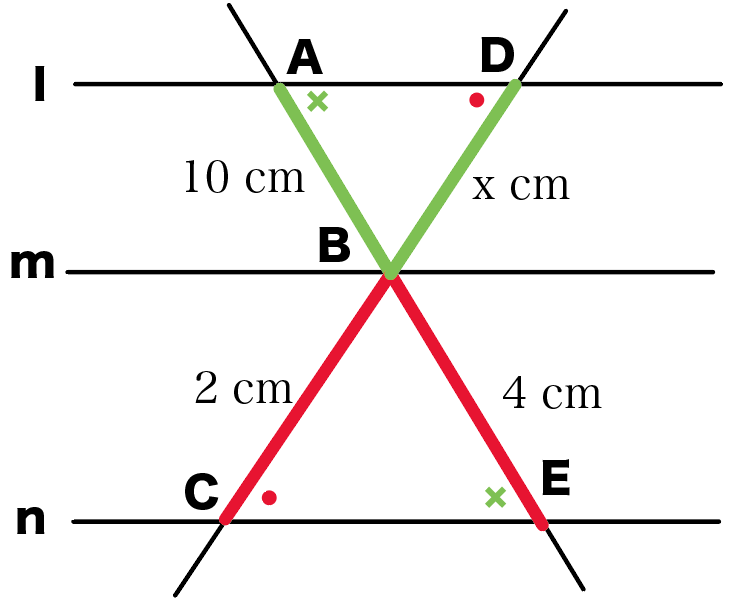
だから、
2組の角がそれぞれ等しい
っていう三角形の相似条件がつかえる。
比例式をといてやると、
AB : BE = DB : BC
10 : 4 = x : 2
4x = 20
x = 5
になるね。
まとめ:平行線と線分の比の問題は対応する辺をみつけろ!
平行線と線分の比の問題は、
対応する辺の比をいかにみつけるか
がポイント。
最後の最後に練習問題を1つ!
練習問題
l//m// nのとき、xの大きさを求めなさい。
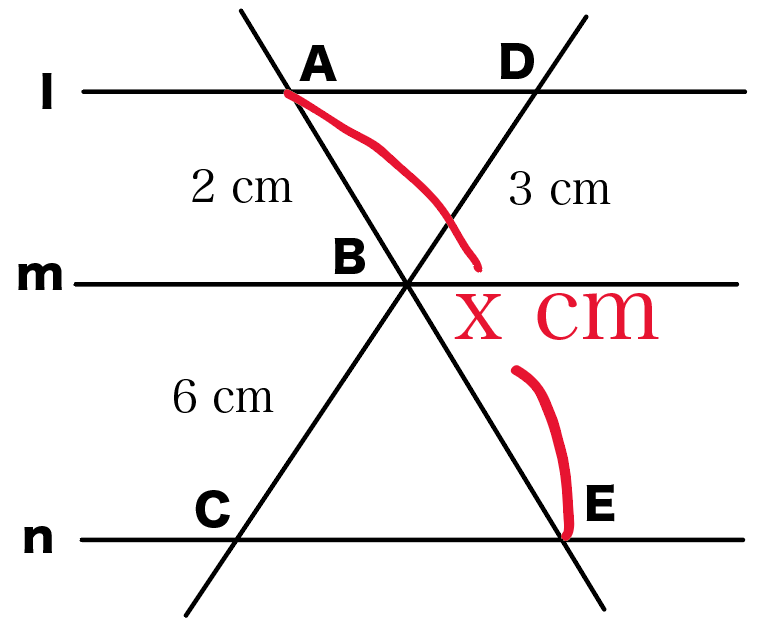
どう?とけたかな??
解答はここをみてみてね。
それじゃあ、また。
ぺーたー


