平行線にはさまれた線分の比の2つの証明
平行線と線分の比の証明ってどうやるの??
やあ、 Dr. リードだよ!!
今日は平行線にはさまれた線分の比の定理を証明するよ。
つぎの2つの定理を証明していくんだ。
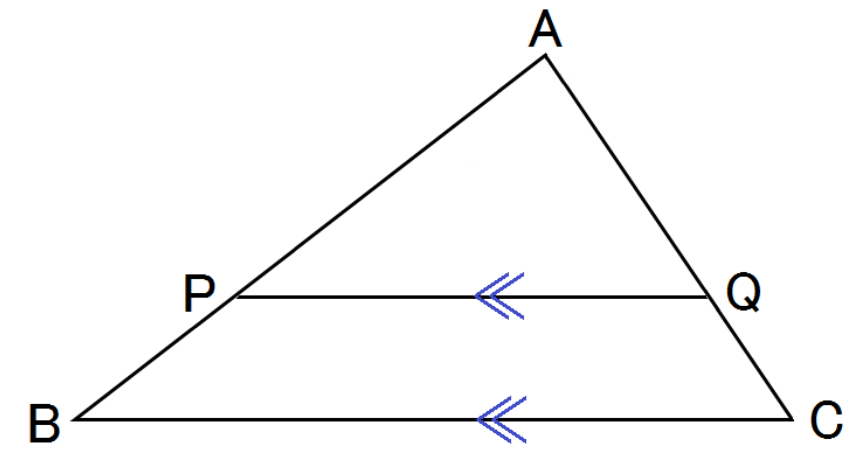
△ABCの辺AB・AC上の点をそれぞれP・Qとするとき、
- PQ//BCならば、 AP:AB = AQ : AC = PQ : BC
- PQ//BCならば、AP:PB = AQ : QC
ところで、今日はケーキを用意したぞ。
最近よく頑張ってるみたいだし。
ごほうびだ。
ちょっと注目して欲しいんだけど、
スポンジとクリームが見事な平行線をつくってるだろ。
「クリーム」と「スポンジの切り口」の長さは左側でも右側でも、
それぞれ一緒だろ?
よ~く目に焼き付けといてくれよ。
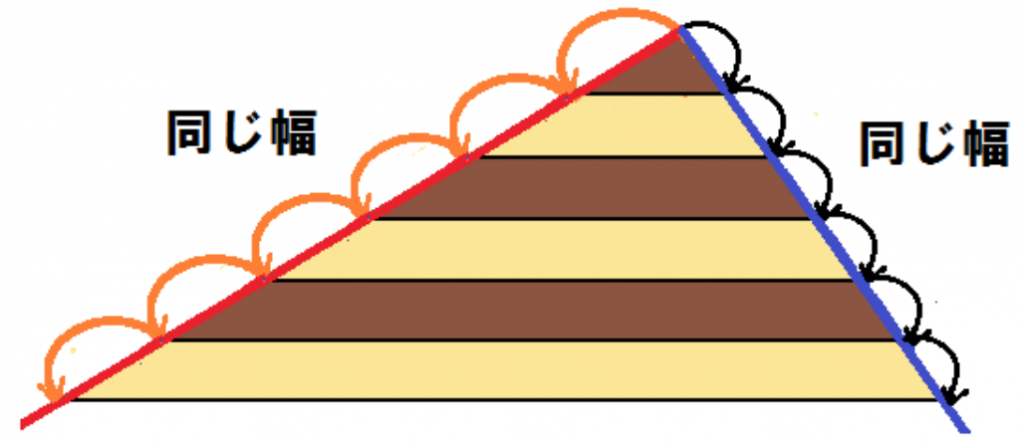
平行線と線分の比の定理を忘れそうになったときは、
カットしたケーキをイメージしてくれよな。
3分でわかる!平行線と線分の比の2つの証明
さっそく、2つの定理の証明をしていくぞ。
証明1.「PQ//BCならば、 AP:AB = AQ : AC = PQ : BC」
平行線と線分の比の証明の1つめ。

△ABCの辺AB・AC上の点をそれぞれP・Qとするとき、
PQ//BCならば、 AP:AB = AQ : AC = PQ : BC
こいつはズバリ、
で2つの三角形の相似を証明をしていけばいいのさ。
以下、証明な↓↓
△ABCと△APQにおいて、
PQ∥BCなので、
∠ABC = ∠APQ (平行線の同位角は等しい)①
∠ACB = ∠AQP (平行線の同位角は等しい)②
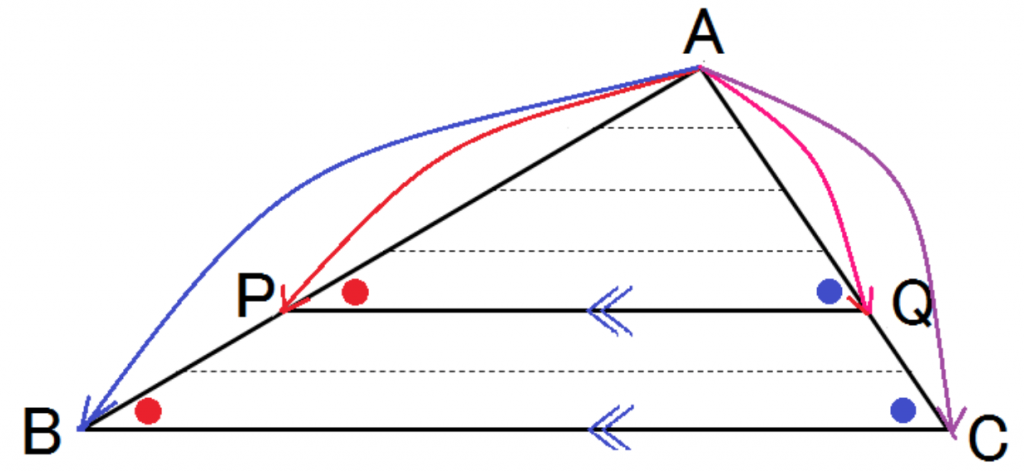
①・②より、
2つの三角形の2組の角がそれぞれ等しいので、
△ABC ∽ △APQ
よって、PQ∥BCならば、
AP:AB = AQ:AC = PQ:BC である。
2つの三角形の相似を証明するだけだから簡単だね。
証明2. 「PQ//BCならば、AP:PB = AQ : QC」
つぎは2つ目の平行線と線分の比の証明だ。

△ABCの辺 AB、AC上の点をそれぞれ点をP・Qとするとき、
PQ // BCならば、
AP : PB = AQ : QC
を証明していけばいいんだね。
まず、補助線を引くぞ。
点Pを通り辺ACに平行な直線PRを引いてみるよ。
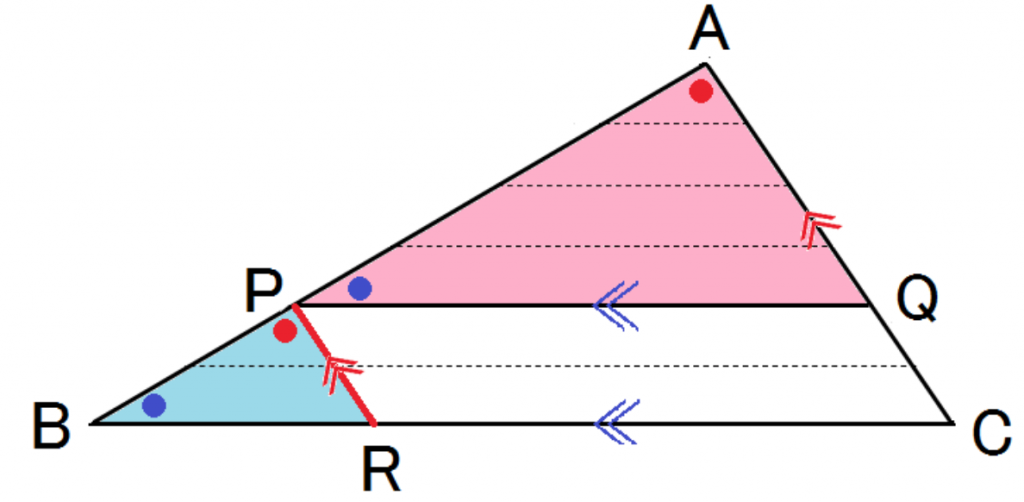
以下、証明な↓↓
△APQと△PBRについて、
PQ∥BCなので、
∠APQ=∠PBR(平行線の同位角は等しい)①
PR∥ACなので、
∠APQ=∠PBR(平行線の同位角は等しい)②
2つの三角形の2組の角がそれぞれ等しいので
△APQ ∽ △PBR
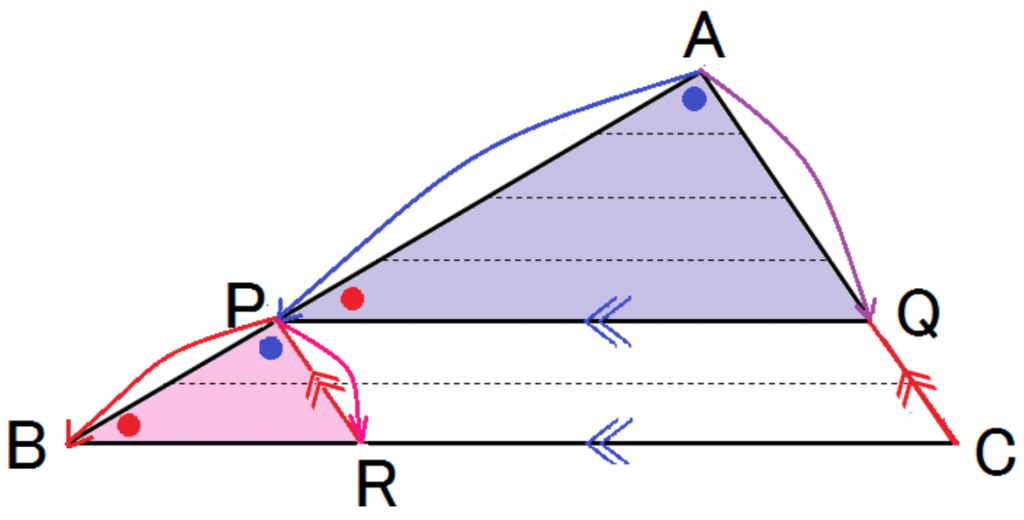
よって、AP:PB = AQ:PR・・・ ③
また,PQ∥BC,PR∥ACなので、
四角形PRCQは平行四辺形で、
PR = QC・・・④ (平行四辺形の向かい合う辺の長さは等しい)
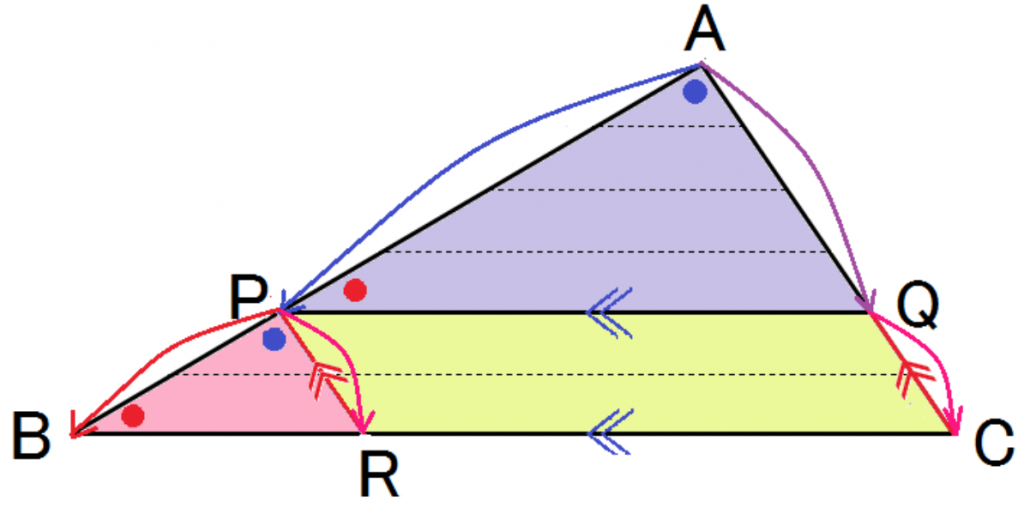
③と④より、
AP:PB = AQ:PR = AQ:QC
やった!
平行線と線分の比の証明もできるようになったね。
まとめ:平行線と線分の比の証明は2種類抑えておこう
平行線と線分の比の証明はどうだったかな?
定理①はすぐ思い浮かぶけど、定理②は忘れちゃいがち。
2つの定理に共通してるのは、
同位角をつかって三角形の相似を証明する
ってこと。
しっかり覚えてくれよ。ケーキだよ。ケーキ。
今回はここまでね。
じゃ、お茶にしよう。


Dr.リード


