【中3数学】2分でわかる!中点連結定理とは??
中点連結定理とはなんだっけ?
こんにちは!この記事を書いてる Kenだよ。ゆれた、ね。
中3数学で相似を勉強していると、
中点連結定理(ちゅうてんれんけつていり)
を習うよね??
中点連結定理とはその名前の通り、
三角形の辺の中点を連結したときに使える定理のこと
をいうんだ。
三角形の2つの辺の中点を結んであげるとね、
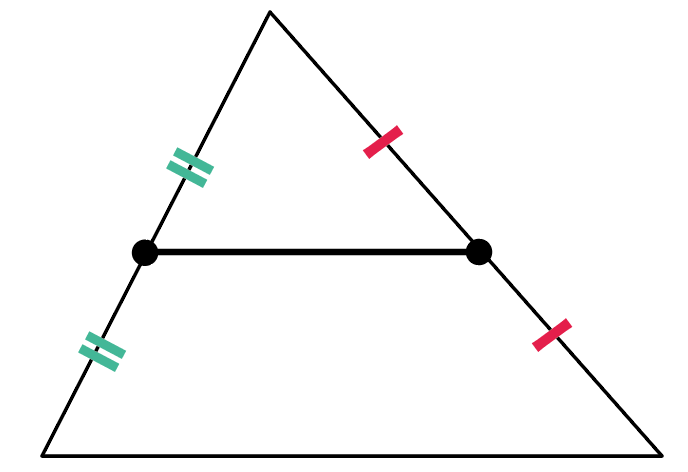
なんと、その中点を結んでできた辺の長さは、底辺の長さの半分になっていて、
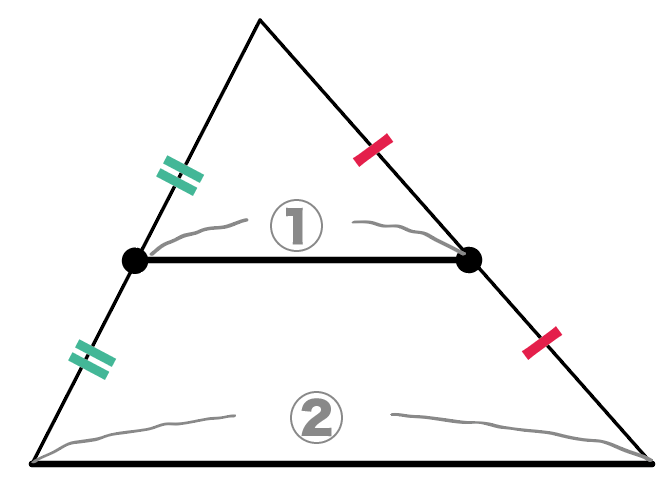
なおかつ、底辺と平行になっているんだ!
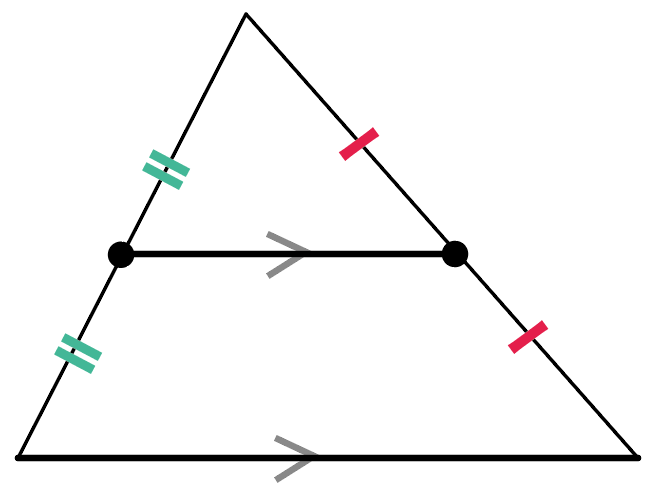
これが中点連結定理の正体。
つまり、中点連結定理の中身を開けてみると、おもに2つに分かれてるわけ。
- 長さについて
- 平行かどうかについて

三角形の中点を結ぶだけで底辺の半分の線が引けて、しかも、そいつは底辺に平行でもあるっていうんだ。
むちゃくちゃ楽チンな定理だね。
中点連結定理を使うとこうなる!
えっ。中点連結定理は役に立つのかって??
今日はそんな疑ってるみんなのために、実際に中点連結定理を使ってみよっか。
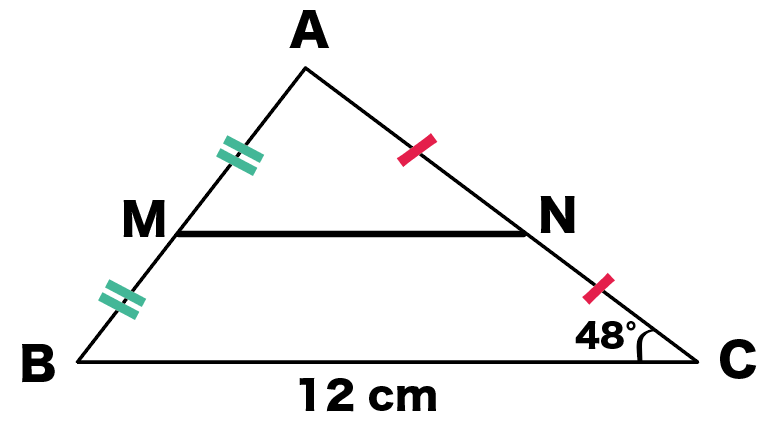
つぎの△ABCを想像してみて。
- AB = 6cm
- BC=12cm
- AC = 8cm
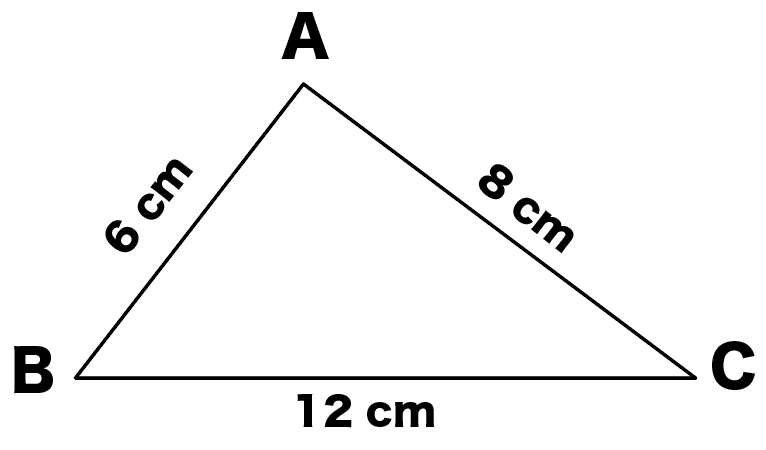
こいつの、辺 ABとACの中点 Mと Nを結んでみたんだ。
∠ACB=48°のとき、
- MNの長さ
- ∠ANMの大きさ
を求めてみよっか!
MNの長さを求める
まずはMNの長さを求めてみよう。
MとNはそれぞれ三角形の辺の中点だから、さっき勉強した中点連結定理が使えるね。
中点連結定理では、三角形の辺の中点を結ぶと、
「結んだ線分の長さ」は「底辺の半分の長さ」になる
って習ったね?
だから、MNの長さは底辺BCの半分になるはずなんだ。
よって、
MN = 1/2 BC = 12×1/2 = 6cm
になるよ。
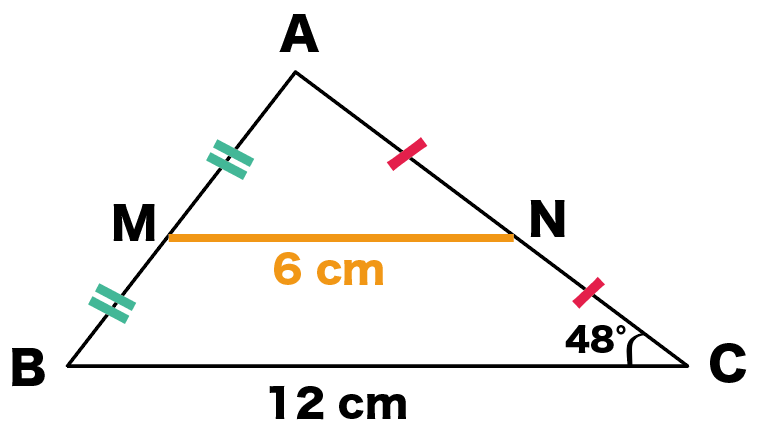
中点連結定理を使ってやると、中点を結んだ線分の長さを1秒ぐらいで計算できちゃうんだ。
ね?便利でしょ??
∠ANMの大きさを求める
つぎは、∠ANMの大きさを求めてみよっか。
中点連結定理のもう1つの性質の、
三角形の辺の中点を結んだ線分は底辺に平行になる
を使うと求めることができるよ。
MとNは△ABCの辺のそれぞれ中点になってるよね??
だから、中点連結定理を使うと、
MN//BC
ってことがわかる。
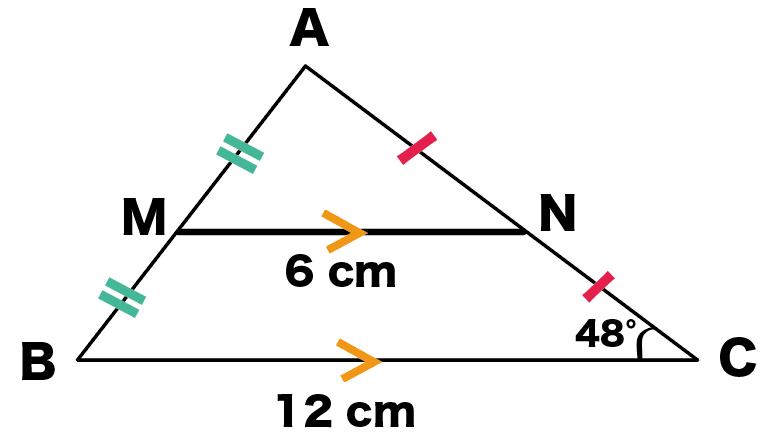
平行な線分同士の同位角は等しいから、同位角の位置にある、
- ∠ANM
- ∠ACB
は等しいはずなんだ。
問題によると、∠ACB = 48° だから、
∠ANM = ∠ACB = 48°
になるってわけ!
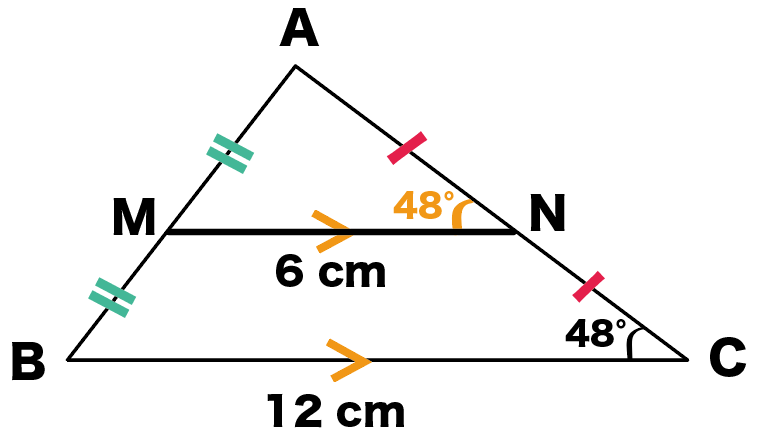
やったね!
これで中点連結定理の平行になる性質も使うことができた!
まとめ:中点連結定理を使うと中点を結んだ線分が詳しくわかる!
中点連結定理はどうだったかな?
最後にもう一回復習しておこっかー!
【中点連結定理】
三角形の2辺の中点を結ぶと、
結んでできた線分は、底辺の長さの半分になり、
しかも、底辺に平行である。

中点連結定理を使った証明問題はよく定期テストにも出てくるから、しっかりおさえておいてね。
そんじゃねー
Ken


