【中学数学】円周率π(パイ)の意味を簡単にいうと??
円周率の意味とはなんだろう!?よくわかんね。
こんにちは、この記事をかいているKenだよ。メガネ探知機がほしいね。
今日から「円とおうぎ形」を勉強していくよ。この単元でいちばん出現するのは、
そう、
円
だ。
円。まるっこい奴のことさ。
教科書によると、
中心Oと円周上の点を結ぶ線分の長さは、円周上の点をどこにとっても等しく、この円の半径になります。
って書いてあるね。
つまり、ただ丸っぽいだけじゃなくて、中心から等しい距離に線をかきまくってできる図形のことなんだ。
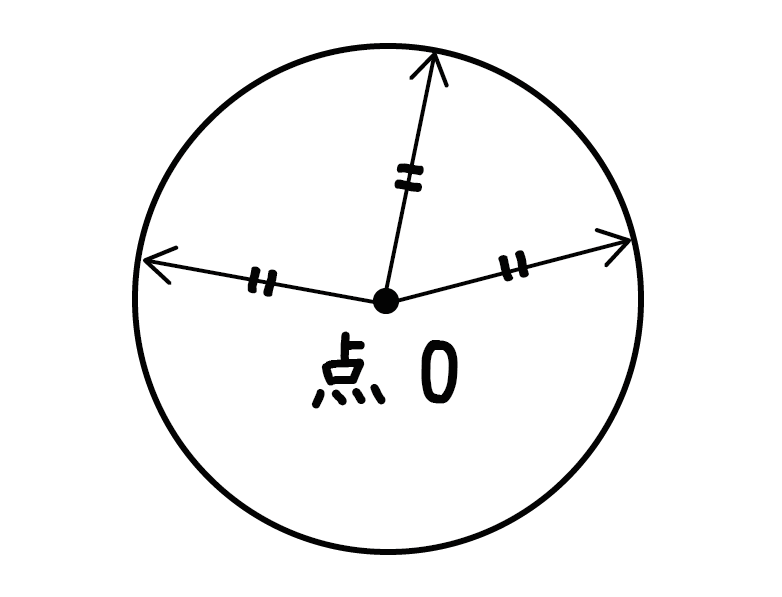
これが「円」だ。
この円について勉強していく上で、知っておくべき用語の1つに、
円周率
っていうものがある。これがむちゃくちゃ重要。円周率を知らないとテストで一問も解けないままゲームセットになっちまうんだ。

それじゃあ、円周率の意味とはなんだろう!??
円周率とは○○の意味がある。
教科書で「円周率の意味」を確認してみよう。中1数学の教科書には、
円周の直径に対する割合です
って説明があるね。円周の直径に対する割合?? えっと・・・ちょっと意味がよくわからないよね。うん、堅苦しい。
もっとわかりやすくいうと、円周率とは、
円周(円のまわりの長さ)が直径の何倍になっているか
ということを表した数字なんだ。小学校のとき、円周率は約3.14って習ったでしょ?? つまり、
円周は直径のだいたい3倍の長さになっているよ。
ってことなんだ。
たとえば、直径1cmの円があったとしよう。
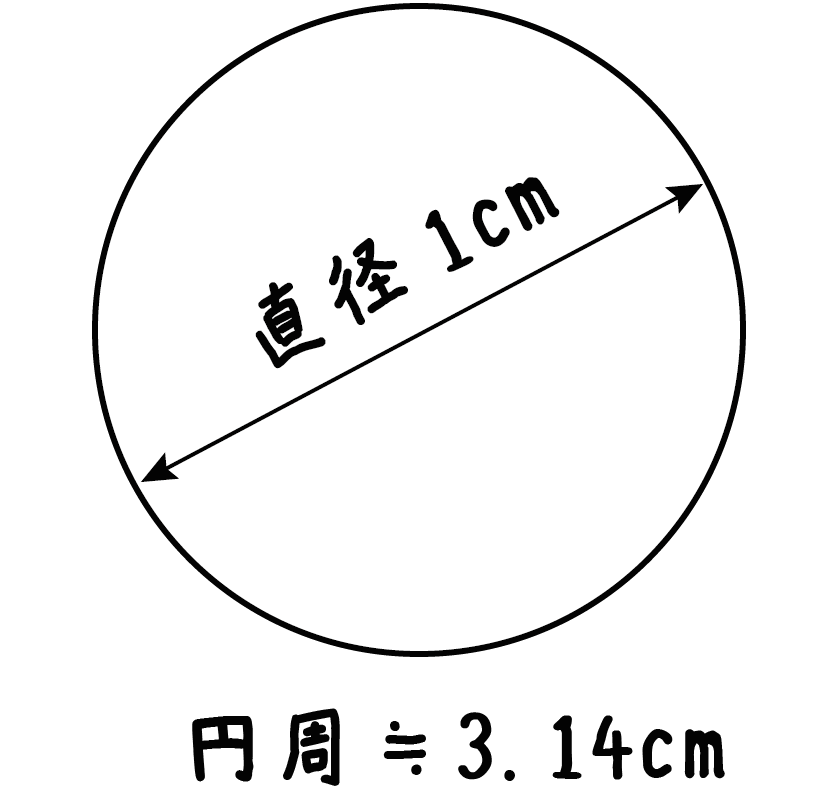
この円周の長さはだいたい3.14cmってことになるわけ。
じつは、この円周率っていうのはむちゃくちゃすごいことなんだ。
なぜかっていうと、
円の大きさを変えても円周率は変わらないからね。たとえば、「小さい円」でも「大きい円」でも決まって、直径の3.14倍が円周の長さになっているんだ。
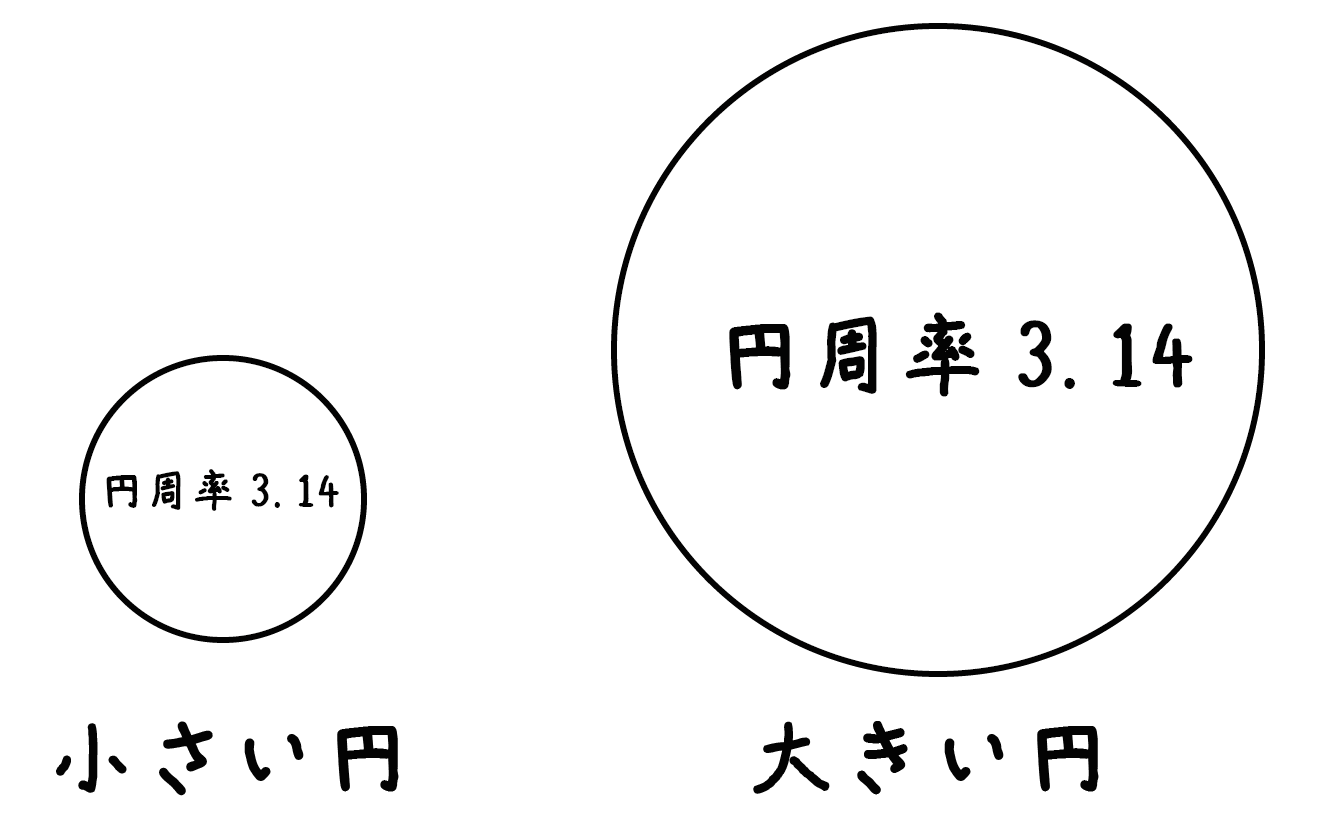
どんなに大きさを変えても「直径」と「円周の長さ」の関係が変わらない。
これってスゴイよね?? もはや地球の神秘のひとつといってもいいぐらいさ。
中学数学では円周率を「π(パイ)」とする
小学校の算数では、
円周率は3.14である
って教わってきたよね。
だけれども、超厳密にいってしまえば、円周率は3.14じゃあない。
円周率は無限につづく終わりがない数字(無理数)なんだ。
3.14のつづきをちょっと書いてみると、
3. 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502….
こんな感じで無限につづいていくんだ。
マジ、終わりがない。
円周率って3.14に近い数字だけれども、3.14ではないんだ。でも、いちいち円周率を長く書いていたらテスト用紙がいくらあっても足りない。
そこで中学数学では、
ギリシャ文字のπ(パイ)
を円周率としてあげることにしたんだ。パイって食べるお菓子のことでもないし、ドラゴンボールにでてくるタオパイパイでもない。
したがって、
円周の長さは直径のπ(パイ)倍である
ってことが言えるね。
まとめ:円周率は「円周と直径の比」である
円周率の意味についてちょっとスッキリしたかな??
次回はいよいよ円の面積・円周の長さの求め方についてみていこう。
そんじゃねー
Ken


