数学の証明問題の解き方がわかる4つのステップ
数学の証明問題の解き方がわからない!
こんにちは!この記事をかいているKenだよ。生姜焼き、食べ過ぎたね。
数学の証明問題ってむずいよね??
計算問題とはひと味ちがう。
どうやって解いたらいいのかわからない。
このままでは数学が嫌いになっちゃいそうだよ・・・・

そこで今日は、
中2数学で勉強する証明問題の解き方を4ステップで解説していくよ。
よかったら参考にしてみてね。
数学の証明問題の解き方がわかる4つのステップ
例題の証明をときながらみていこう!
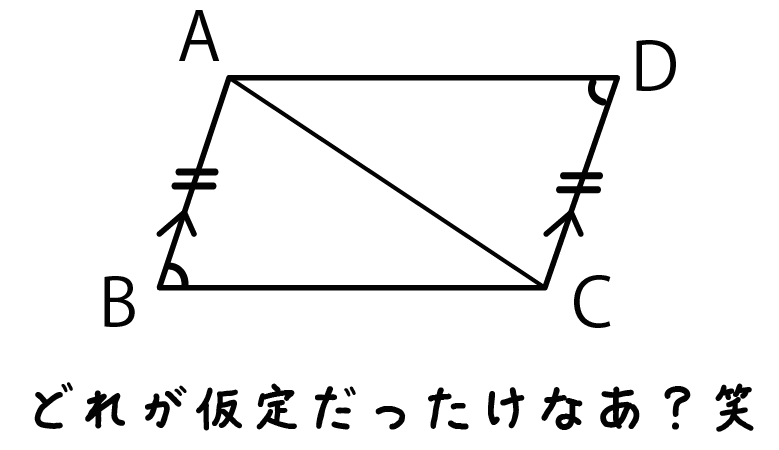
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、角ABC = 角CDAであることを証明しなさい。
Step1. 仮定と結論を整理する!
まずは仮定と結論を整理しよう。
仮定と結論って簡単にいってしまうと、
- 「仮定」=「問題文からすでにわかっていること」
- 「結論」=「証明のゴール」
だよ。
証明問題において、
なにを説明できればゲームクリアなのか??
そのために、どんな条件があたえられているのか???
を整理することはむちゃ大事なんだ。
例題で実際に、
仮定と結論を整理してみよう。
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、角ABC = 角CDAであることを証明しなさい。

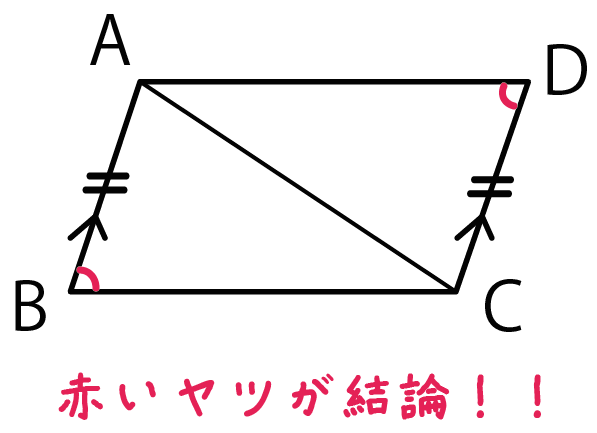
- AB = DC
- AB//DC
は問題文でわかっていることだね。
つまり、こいつらが「仮定」さ。
一方、結論は、
- 角ABC = 角CDA
だ。
証明問題の「結論」って、
○○であることを証明しなさい
の「○○」にかいてあることが多いよ。

どうしても結論がみつからないときは、
問題文を読み返してみてね。
Step2. 仮定を図にかきこむ!
仮定を図にかきこんでやろう。
かきこむだけで、
仮定と結論がわかりやすく整理できて、
解き方のイメージをしやすくなるんだ。
ただここで注意してほしいのは、
仮定と結論をごっちゃまぜにしないことだ!
同じ黒ペンで仮定と結論をかきこむのはNG。
仮定と結論がどっちなのかわからなくなるからね。
だから、
仮定と結論を色違いのペンで書き込むことをおすすめするよ。
えっ、書き込まなくてもすでに整理できてるって??
そういうヤツはこのステップをとばしてくれ。
つぎにいこう!
Step3. 結論までの道のりをイメージする
仮定・結論をみつめて、
どうやって仮定から結論までもっていくか??
をイメージするんだ。

具体的にいうと、
結論をいうために、
「根拠となることがら」は何をつかうか??
を考えることになるよ。
例題をみてみよう。
例題の結論は、
角ABC = 角CDA
だったよね?
うーん、
どうしよー、
うーん、
・・・・・
は!
これだ!
△ABCと△DACが合同であることをいえば
「角ABC = 角CDA」がいえるかも!!
合同な図形同士の対応する角の大きさが等しい
って根拠をつかえばね。

って感じで、
どの根拠をつかえばゴールの結論にたどり着けるか?
を事前にイメージしていくんだ。
Step4. 書き方にどおりにかく!
後は証明を書くだけ!
証明の書き方には型がある。
それ通りにかいていけばいいんだ。

証明の書き方はつぎのようになっているよ。
- 問題文でわかっていること(仮定)
- 仮定からわかること
- 根拠となることがら
- 結論
この4つを詰め込んでやれば大丈夫だよ。
書き方は先生によって違うから、
担当教師の書き方をマネしてみてね。
例題の答えをかいてみるよ。
ぼくだったらつぎのような感じでかくね。
△ABCと△CDAにおいて、
AB = CD (仮定)・・・(1)
AC = CA (共通)・・・(2)
AB // CDより、
平行線の錯角が等しいので、
角BAC = 角DCA・・・(3)
(1)、(2)、(3)より、
2辺とその間の角がそれぞれ等しいので、△ABC ≡ △CAD対応する角の大きさが等しいので、角ABC = 角CDA
となる。

問題でわかっていること(仮定)から、
証明問題のゴール(結論)をみちびければいいんだ。
まとめ:数学の証明問題の解き方は整理とイメージが大事!
数学の証明問題の解き方はつぎの4ステップだったね。
- 仮定と結論の整理
- 仮定を図にかきこむ
- 結論までをイメージする
- 書き方にしたがってかく!
証明問題はちょっとむずい。
だけど、解き方さえおさえておけば大丈夫さ。
問題をといて証明になれてみてね。
そんじゃねー
Ken