二等辺三角形の高さの求め方って？？
こんにちは！この記事をかいているKenだよ。ビタミンC摂取したいね。
二等辺三角形の高さを求める問題
ってたまにでる。
たとえばつぎのような問題さ。
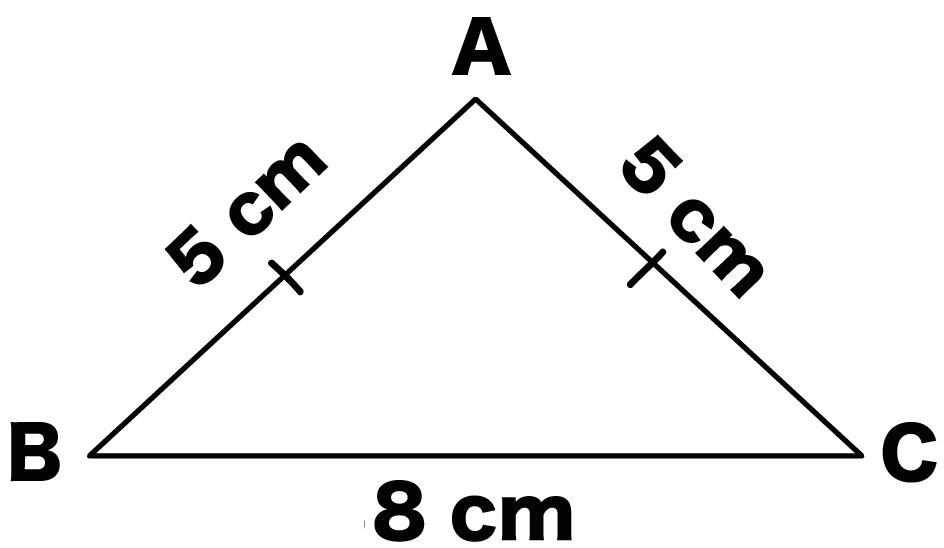
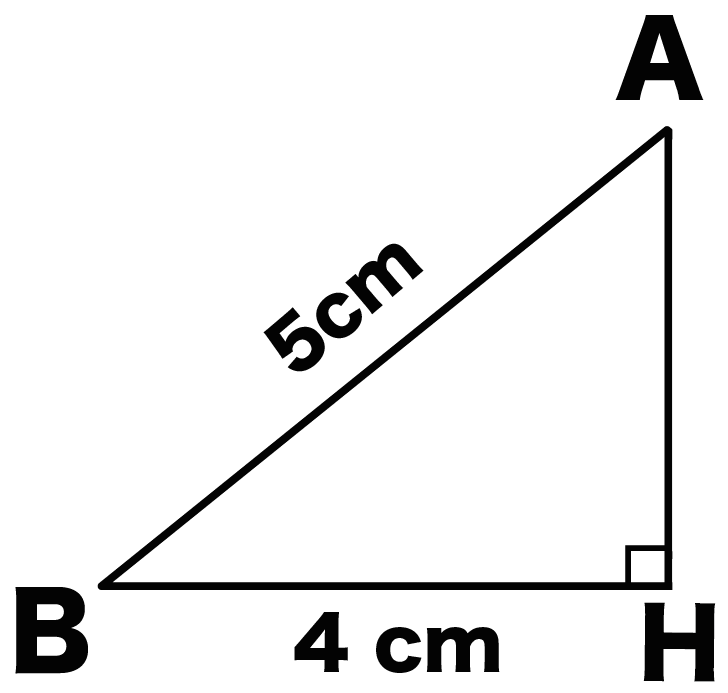
AB = AC = 5cm、BC = 8 cmの二等辺三角形ABCにおいて、
底辺をBCとしたときの高さを求めよ。
この手の問題は簡単そうだね？
だがしかし、意外にやっかいなんだ。
今日はこの問題をわかりやすく解説していくよ。
よかったら参考にしてみて。
二等辺三角形の高さの求め方がわかる3ステップ
例題をといてみよう。
AB = AC = 5cm、BC = 8 cmの二等辺三角形ABCにおいて、
底辺をBCとしたときの高さを求めよ。
つぎの3ステップで計算できるよ。
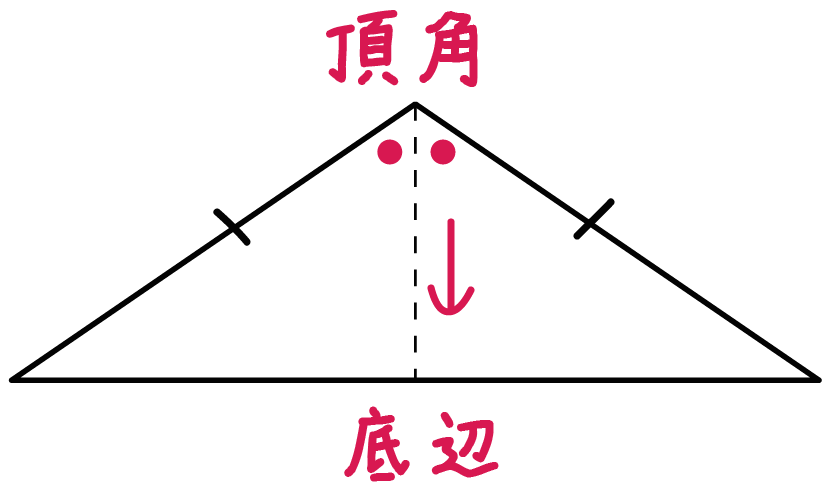
Step1. 頂角から二等分線を底辺にひく
頂角の二等分線を底辺にひいてみよう。
例題でいうと、
頂角Aを二等分する線を、
底辺BCにむかってひいてあげる。
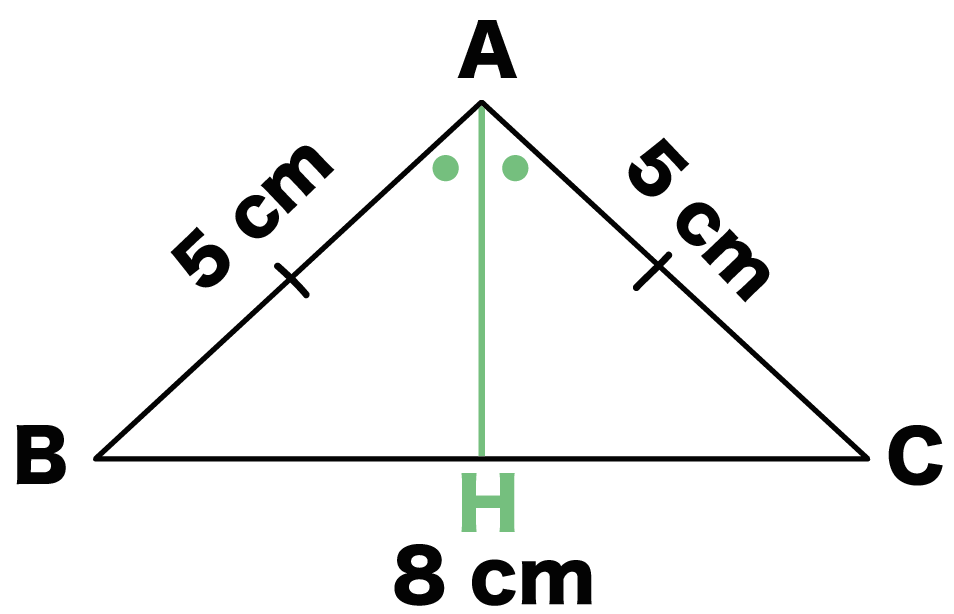
底辺との交点をHとしよう。
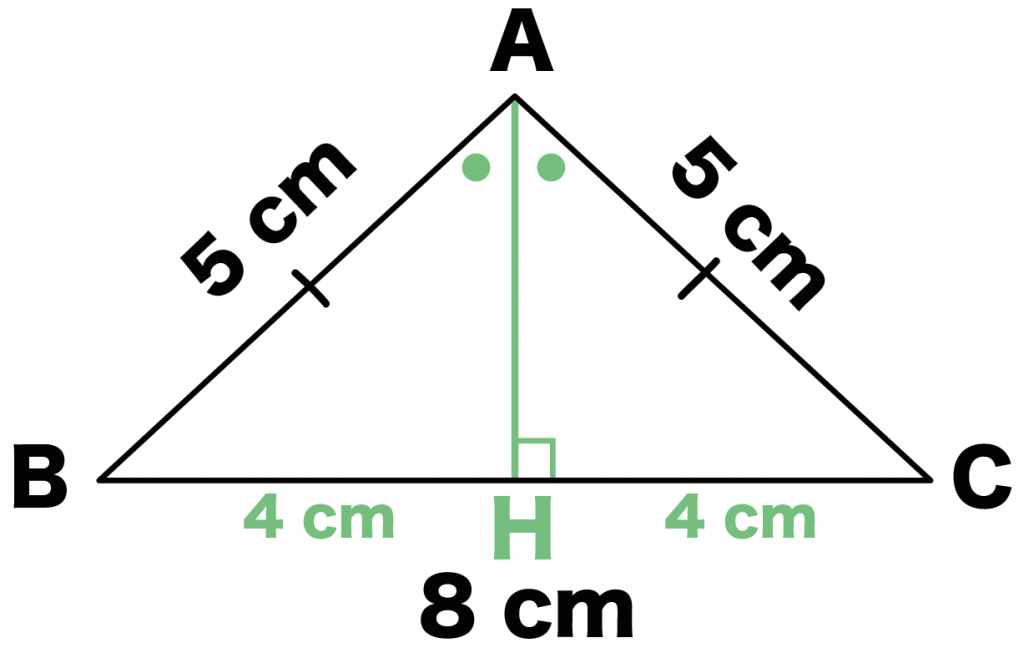
Step2. 底辺の半分の長さを求める！
つぎは底辺の半分を計算するよ！
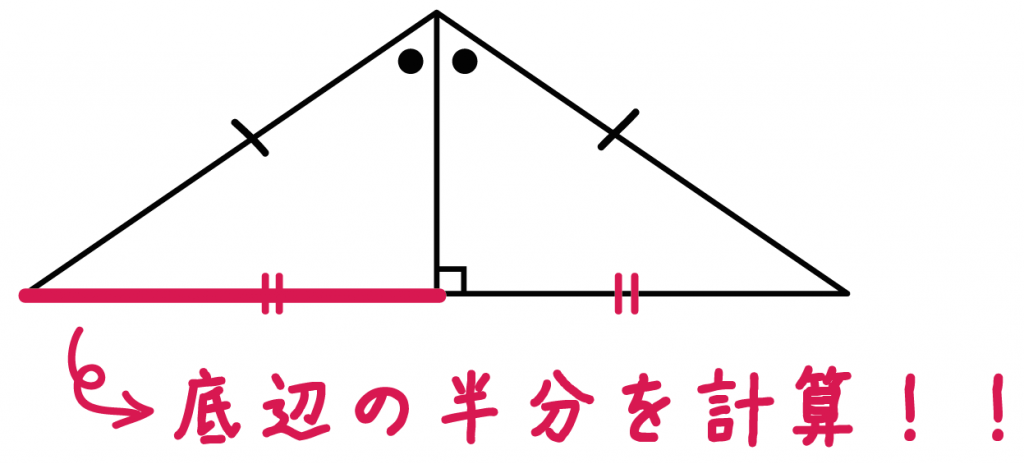
二等辺三角形の性質の中に、
二等辺三角形の頂角の二等分線は底辺を垂直に2等分する
ってやつがあったはずだ。
こいつを使ってやると、
二等分線AHはBCの垂直二等分線になっているはず。
つまり、
- AH ⊥ BC
- BH = CH
ってことさ。
底辺BC = 8cmだから、
BH = CH = 4 cm
だね。
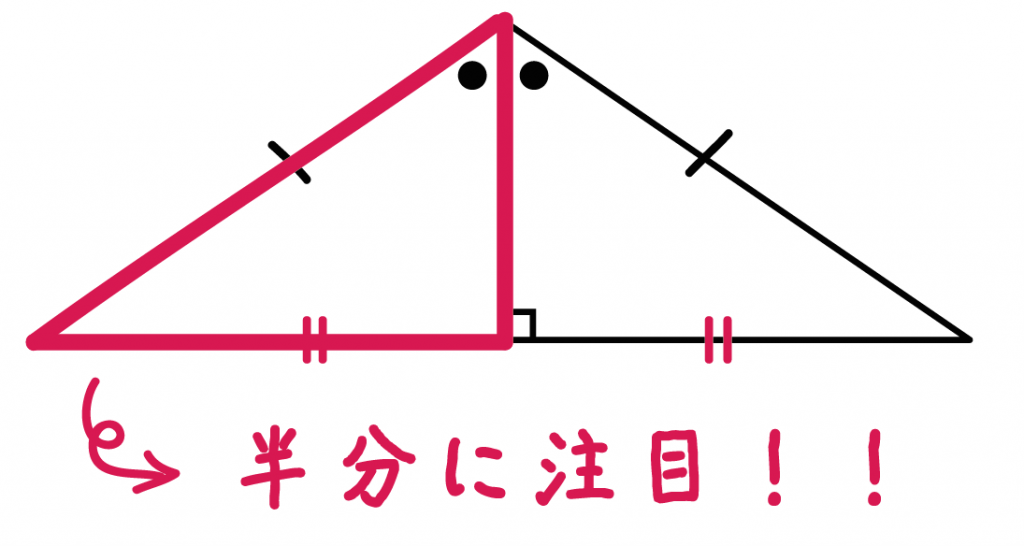
Step3. 三平方の定理で高さを計算！
最後は三平方の定理をつかおう！
半分の三角形に注目してみて。
例題でいうと、
三角形ABHだね。
こいつは、
直角三角形2辺の長さがわかってるね。
ってことは、
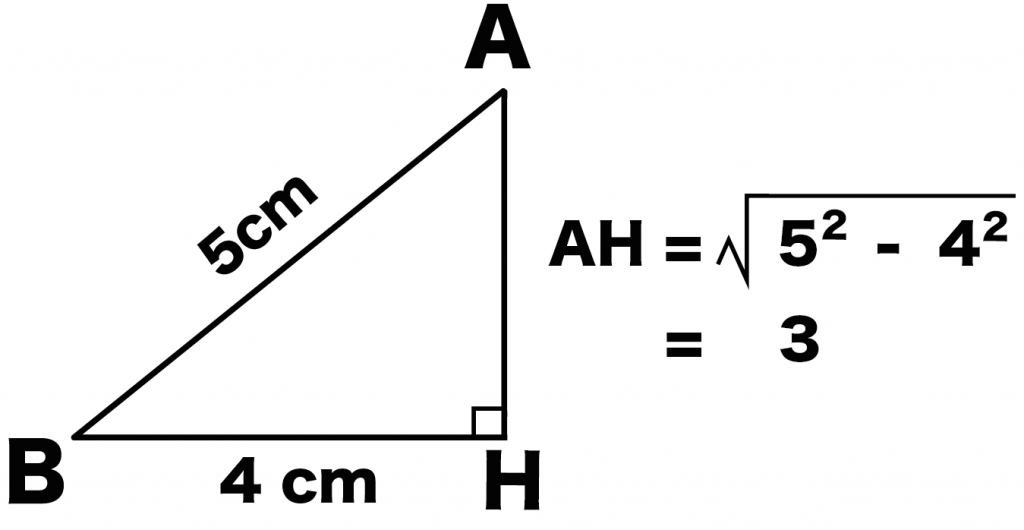
高さAHは三平方の定理をつかえば求められる。
三平方の定理より、
AH = √5^2 – 4^2
= 3
になるね。
おめでとう！
これで二等辺三角形の高さを求められたね！
まとめ：二等辺三角形の高さの求め方は三平方の定理で1発！
二等辺三角形の高さを求めたいときは、
- 頂角の二等分線をひく
- 底辺の半分の長さをだす
- 三平方の定理をつかう
の3ステップで終了さ。
あとは問題に慣れてみてね。
そんじゃねー
Ken
