二等辺三角形の底辺の長さの求め方だって？？
こんにちは！この記事をかいているKenだよ。レトルト、最高。
二等辺三角形の底辺の長さの求め方
って知ってる？？
ふつうに生きるためなら求め方知らなくても大丈夫。
パンがあれば生きていける・・・・
でもでも、
たまーにだけど、
二等辺三角形の底辺の長さを計算する問題
がでてくるんだ。
たとえばつぎのやつね。
例題
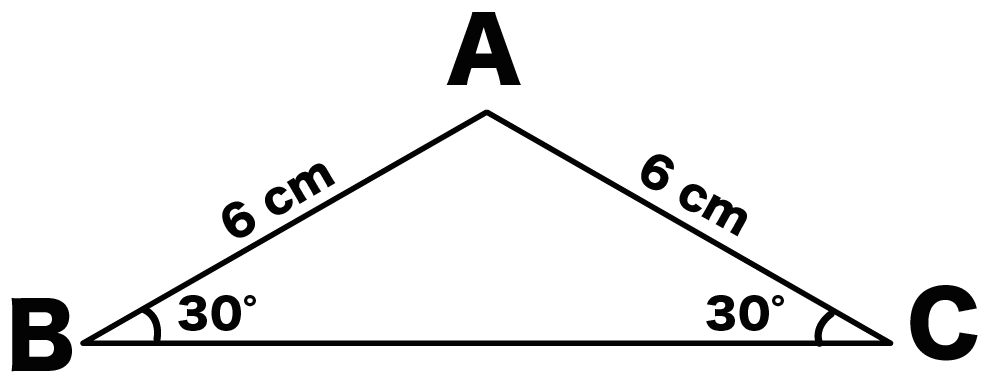
二等辺三角形ABCの底辺BCの長さを求めなさい。
なお、AB = BC = 6 cm、角B = 角C = 30°とします。
今日は、このタイプの問題を攻略するために、
二等辺三角形の底辺の長さの求め方
をわかりやすく解説していくよ。
よかったら参考にしてみて。
二等辺三角形の底辺の長さの求め方がわかる3ステップ
さっきの例題をといてみよう。
例題
つぎの二等辺三角形ABCの底辺BCの長さを求めなさい。
なお、AB = BC = 6 cm、角B = 角C = 30°とします。
つぎの3ステップで計算できちゃうよ。
Step1. 頂角の二等分線を底辺におろす
頂角から底辺に二等分線をかいてみよう。
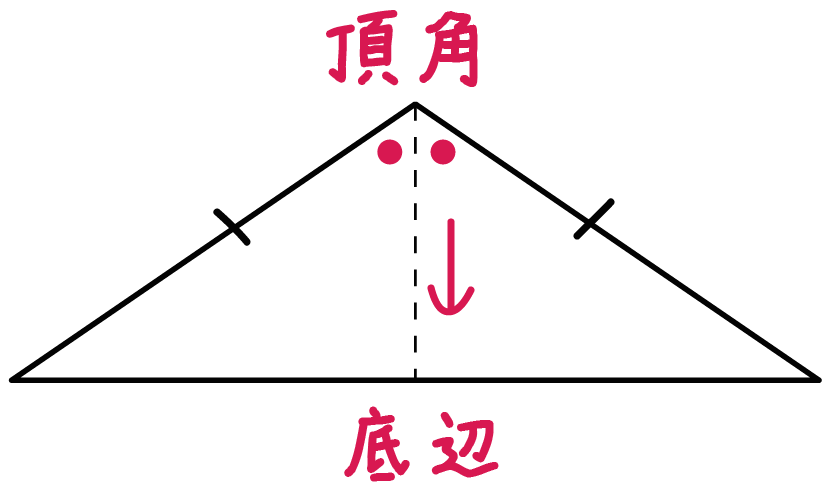
等しい辺にはさまれた角が「頂角」だったね？
そいつを二等分する線を、
底辺におろしてやればいいんだ。
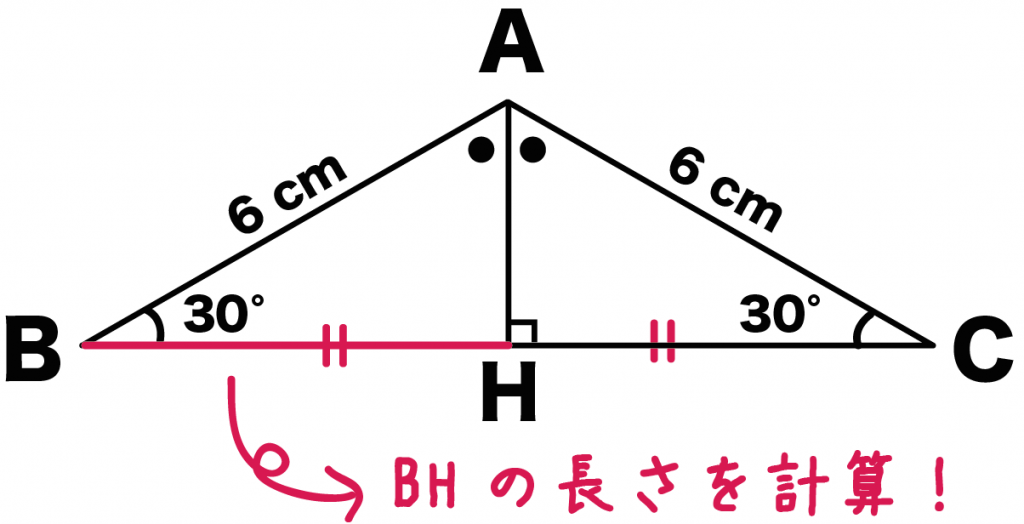
例題をみてみよう。
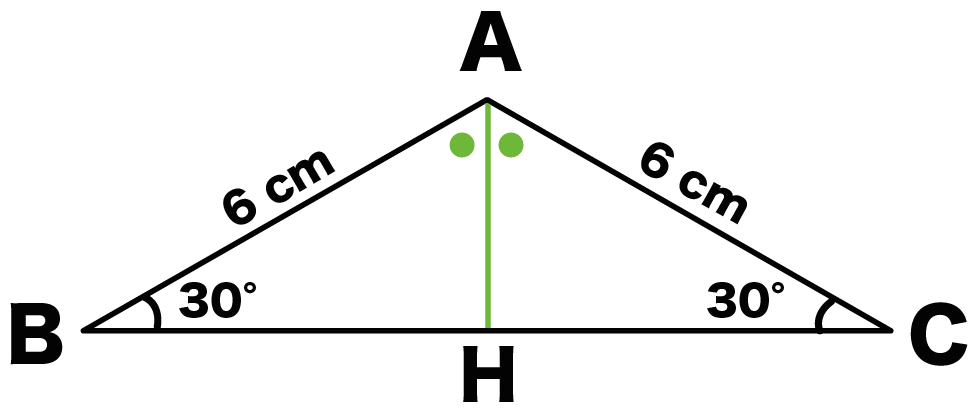
二等辺三角形ABCの頂角はA。
こいつから底辺Bに二等分線をおろそう。
底辺と二等分線の交点をHとすると、
こうなるね↑↑
ちなむと、
二等辺三角形の定理の1つに、
頂角の二等分線は、底辺を垂直に2等分する
ってやつがあるよね？
ってことは、
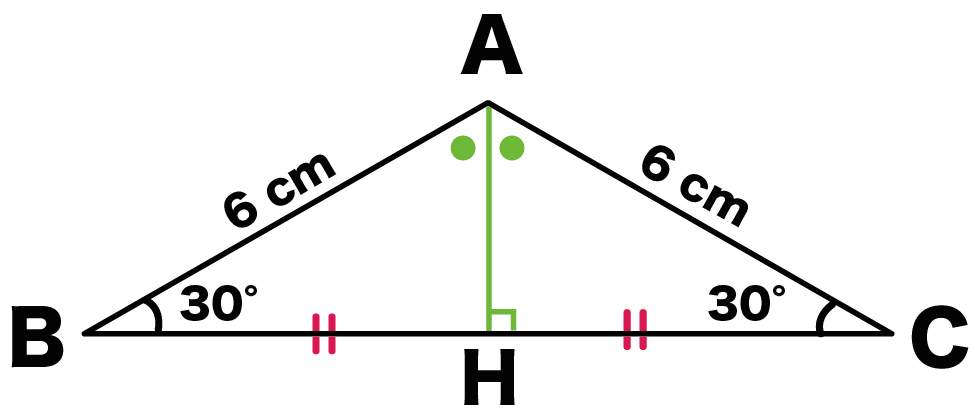
AHはBCの垂直二等分線になっているんだ。
つまり、
- AH ⊥ BC
- BH = CH
になっているのさ。
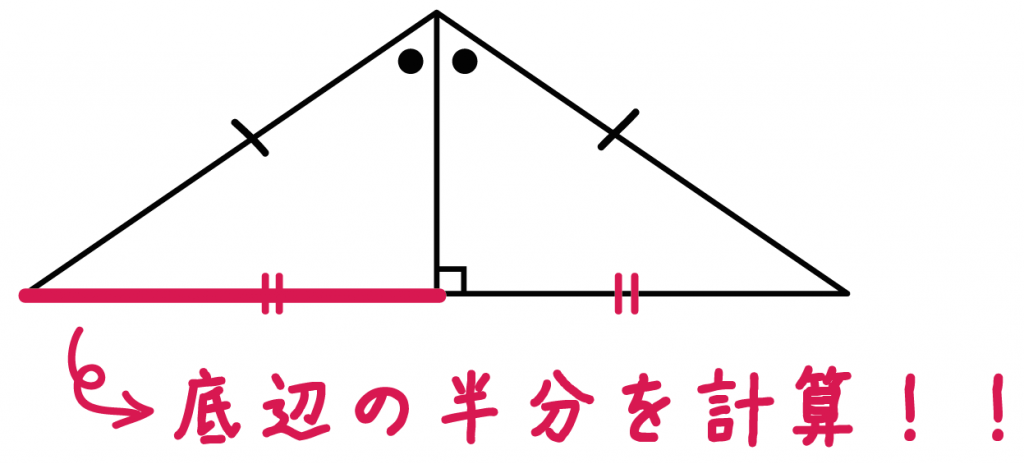
Step2. 底辺の半分の長さを計算する！
底辺の半分の長さを計算しよう。
例題では、
辺BHの長さを計算するよ。
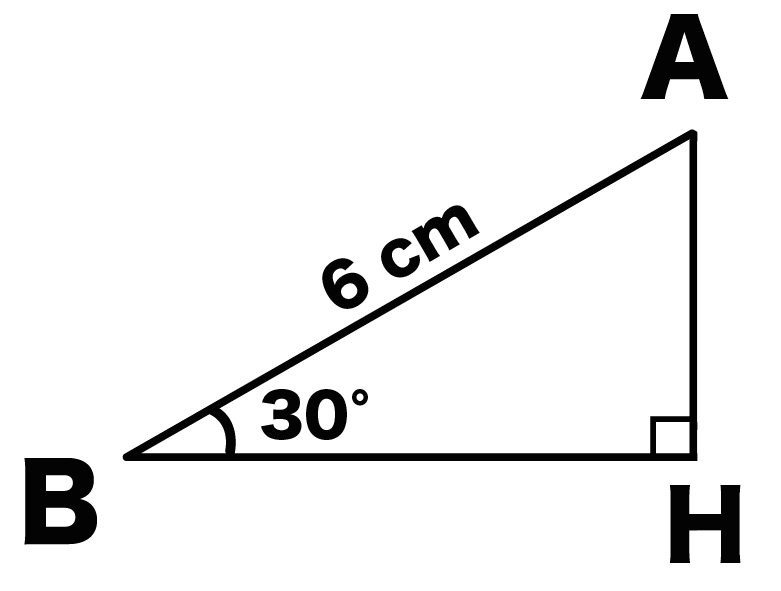
三角形ABHに注目してみると、
30°をもった直角三角形であることがわかるよね？？
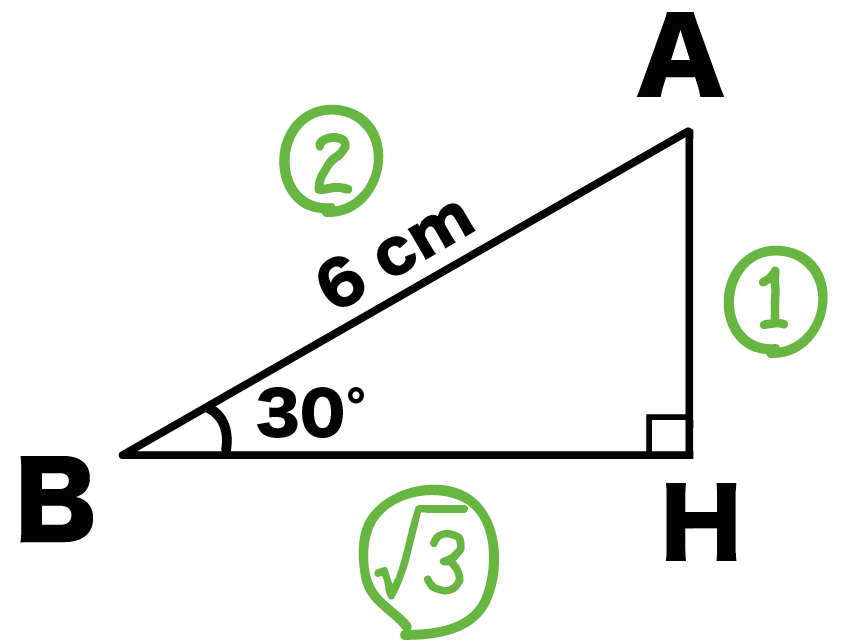
各辺の比は、
1:2: √3
になっているはずだ。
ってことは、
BHの長さを計算すると、
BH = AB × √3 /2
= 3√3
になるね。
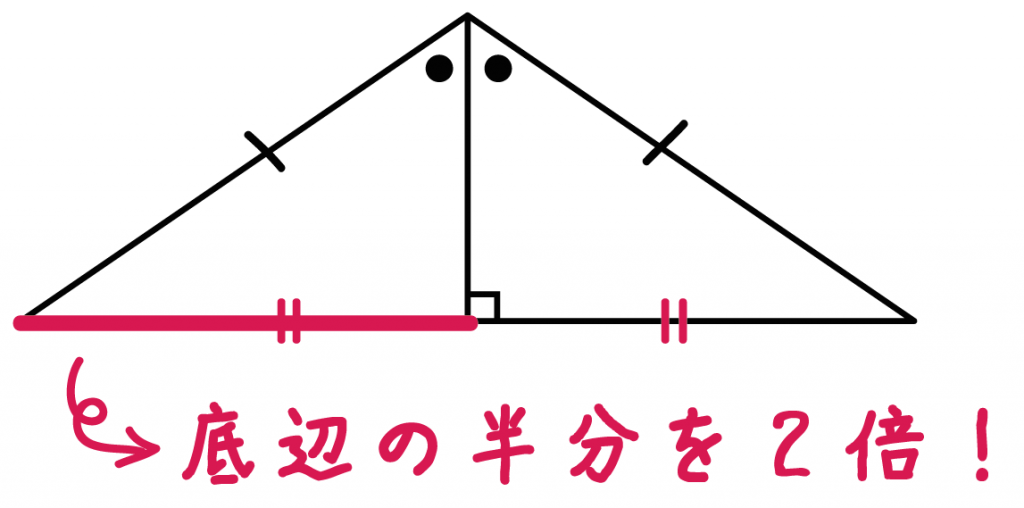
Step3. 「底辺の半分」を2倍する！
さっきもとめた、
「底辺の半分」を2倍してやろう！
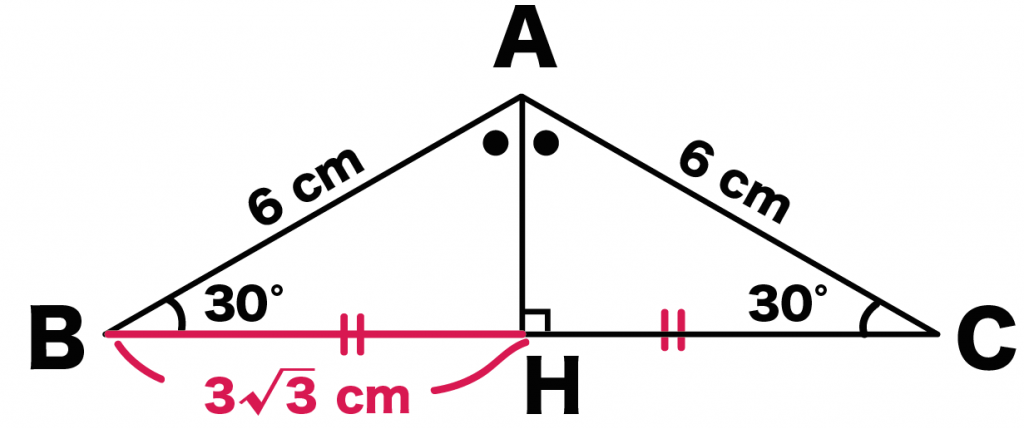
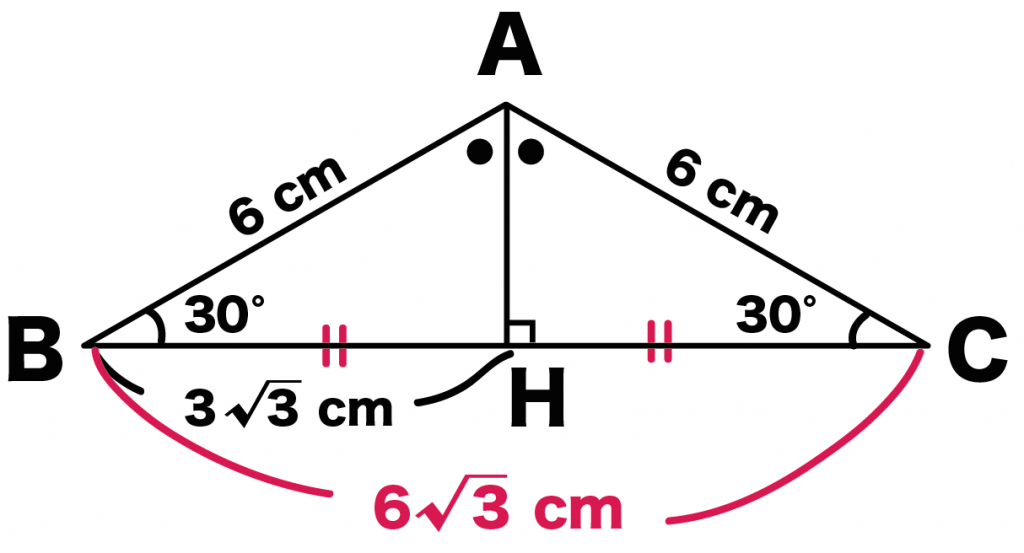
例題では、底辺の半分は「3√3」cmだったよね？
ってことは、
そいつを2倍すると、
BC = 3√3 × 2
= 6√3
になる。
おめでとう！
これで二等辺三角形の底辺の長さを計算できたね！
まとめ：二等辺三角形の底辺は二等分線からはじまる。
二等辺三角形の底辺の計算は簡単。
- 頂角の二等分線を底辺にひく
- 底辺の半分の長さを求める
- そいつを2倍する
っていう3ステップでいいんだ。
どんどん問題をといてみよう！
そんじゃねー
Ken
