これでスッキリ!円周角の定理の証明の3つのパターン
円周角の定理の証明ってどうやるの??
Dr.リードだよっ。
円周角の定理の使い方にも慣れてきたかな?
今日はな、
円周角の定理の証明
を解説していくぞ。
つまり、
なぜ、円周角の定理が使えるのか??
ってことを暴いていくわけだ。
別に知らなくてもいいけど、知っておいた方がスッキリするだろ?
今日は長い長い話になる。
ピザでも食べながら行ってみよう!


円周角の定理の証明の3パターン
「円周角の定理」を証明していくぞ。
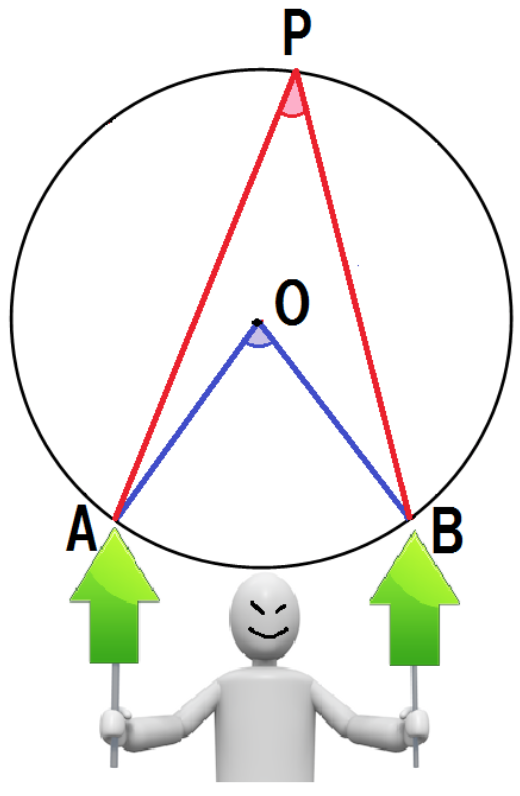
3点A・B・Pがある円Oを想像してくれよな。
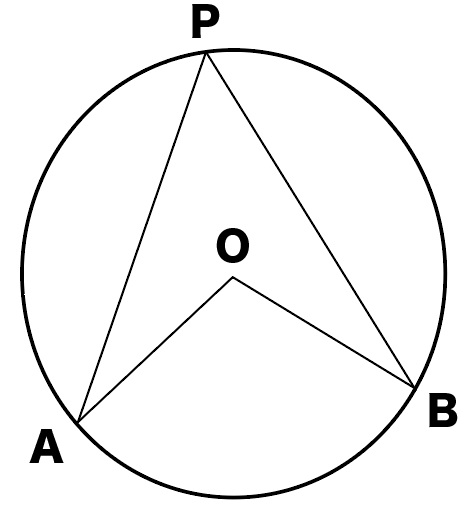
円周角と中心角の位置関係はつぎの3通りある。
- 点 PがOB上にあるとき
- 中心Oが∠APBの内側にあるとき
- 中心 Oが∠APBの外側にあるとき
それぞれの場合を証明していけばいいんだ。
証明パターン1. 「 点PがOB上にあるとき」
まずは点P がOBの延長上にきてる場合ね。
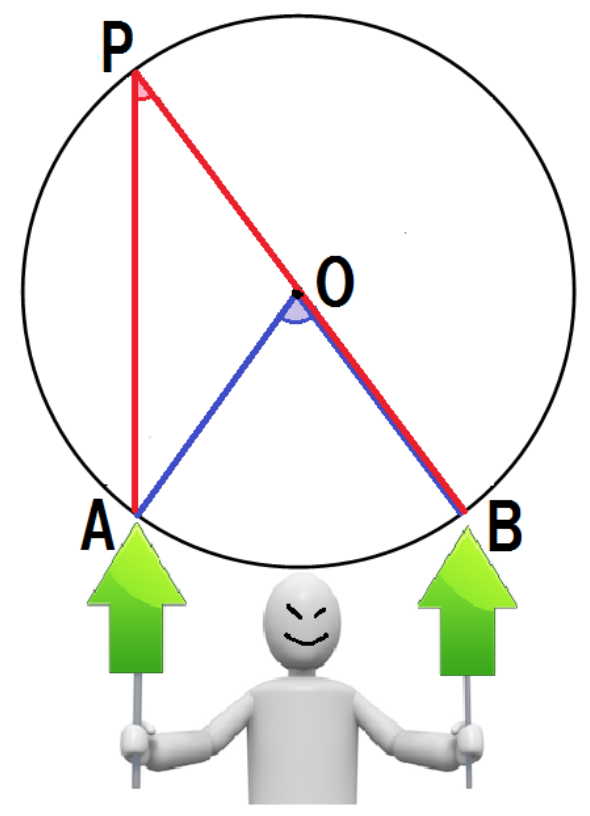
このパターンでは、
をうまく使っていくよ。
えっ。三角形の外角の定理なんて忘れた?!
三角形の1つの外角はそれと隣り合わない2つの内角の和に等しい
っていう定理だったね。
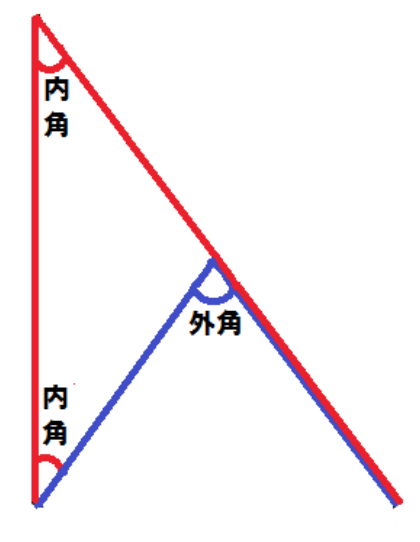
こいつをうまく使って証明してみよう。
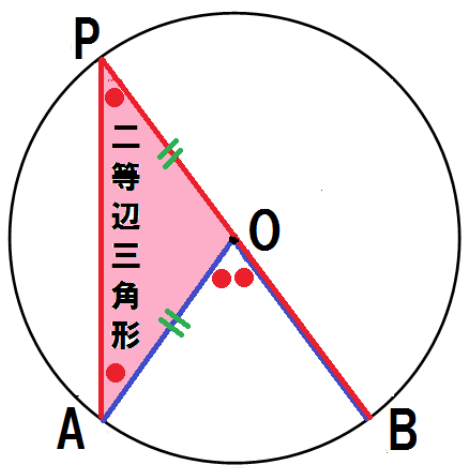
OP・OAはそれぞれ円Oの半径だから、
OP = OAよって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)三角形の外角の定理より、
∠AOB = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APB = 1/2∠AOB
「二等辺三角形の性質」と「外角の定理」を知ってれば証明できるね!
証明パターン2. 「中心Oが∠APBの内部にある」
さあ、サクサク行くぞ。
つぎは、
中心Oが円周角の内部におさまってる形だ。
補助線を緑で引いていくぞ。
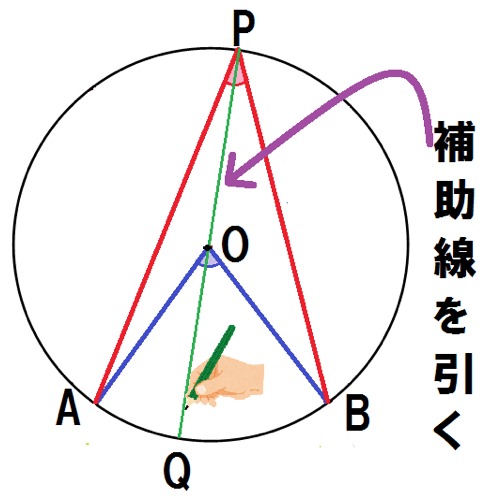
点Pと中心Oを結び延長して、交点をQとしよう。
中心を通るから、PQは円Oの直径ってことになるね。
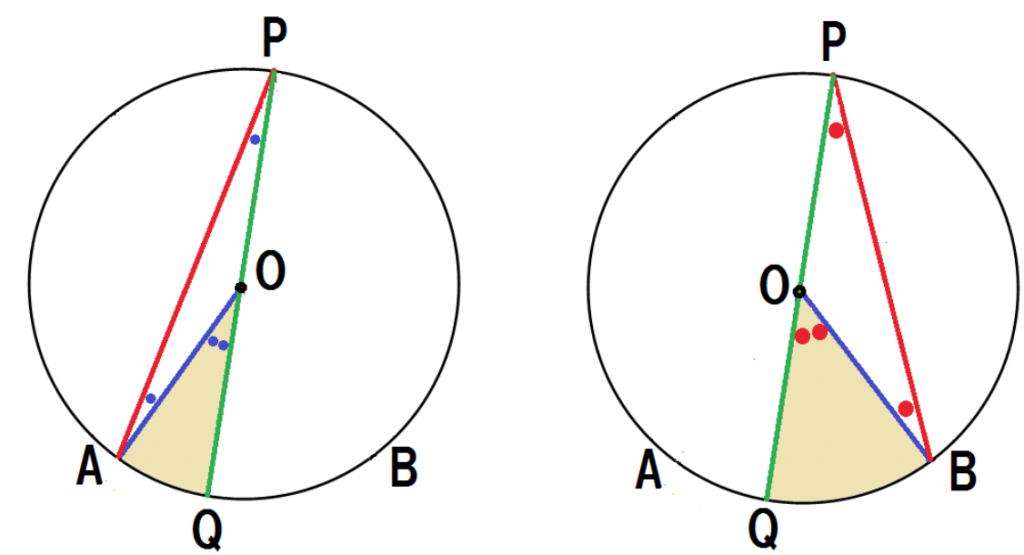
上の図みたいに補助線を中心に2つの図形に分けてみて。
- 左の図
- 右の図
- 合体したやつ
の順番で証明していくよ。
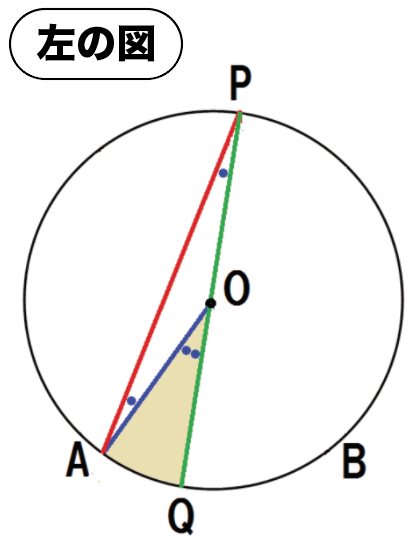
OP・OAはそれぞれ円Oの半径だから、
OP = OA
よって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)
三角形の外角の定理より、
∠AOQ = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APQ = 1/2∠AOQ・・・(3)
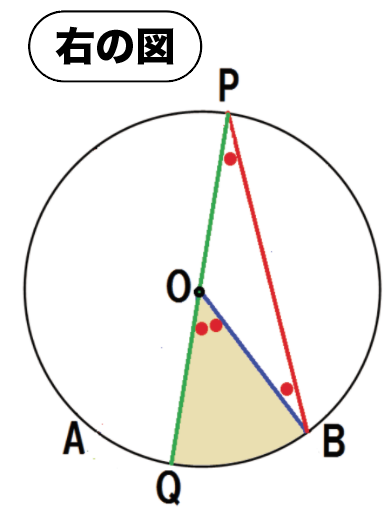
OP・OBはそれぞれ円Oの半径だから、OP = OB
よって、△OPBはOP = OBの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OBP = ∠OPB ・・・ (4)
三角形の外角の定理より、
∠BOQ = ∠OBP + ∠OPB・・・(5)
(4)、(5)より、
∠BPQ = 1/2∠BOQ・・・(6)
で,右半分の図と左半分の図を元通りに重ね合わせると,
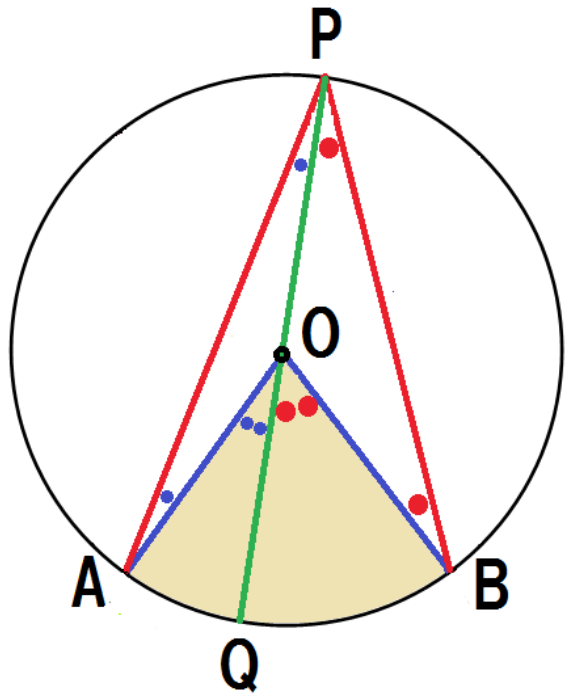
(3)+(6)より、
∠APQ +∠BPQ= 1/2∠AOQ + 1/2∠BOQ
よって、
∠APB = 1/2∠ AOB
よって、
円周角∠APBは中心角∠AOBの半分である。
証明パターン3. 「中心Oが∠APBの外部にある」
最後は、
中心Oが∠APBの外にあるパターンね。
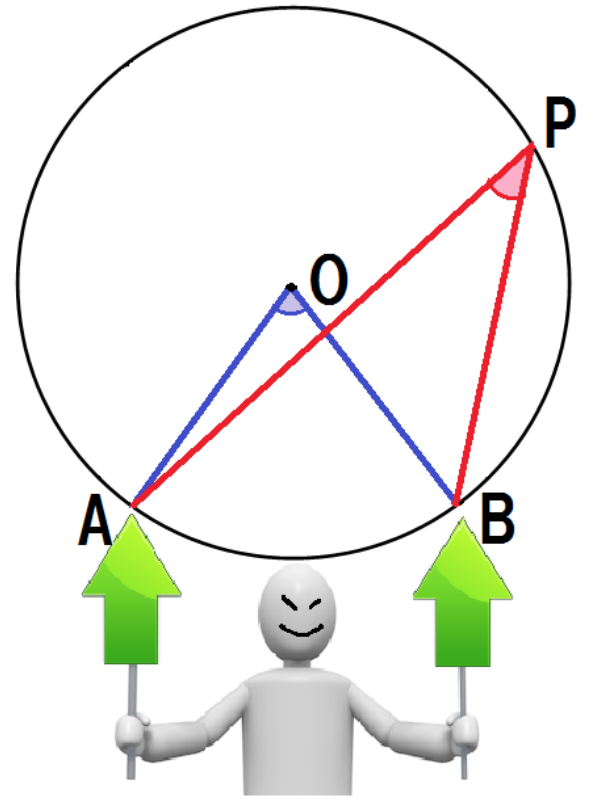
またまた補助線引くよ。
OPを延長した線分と円周の交点をQとするぞ。
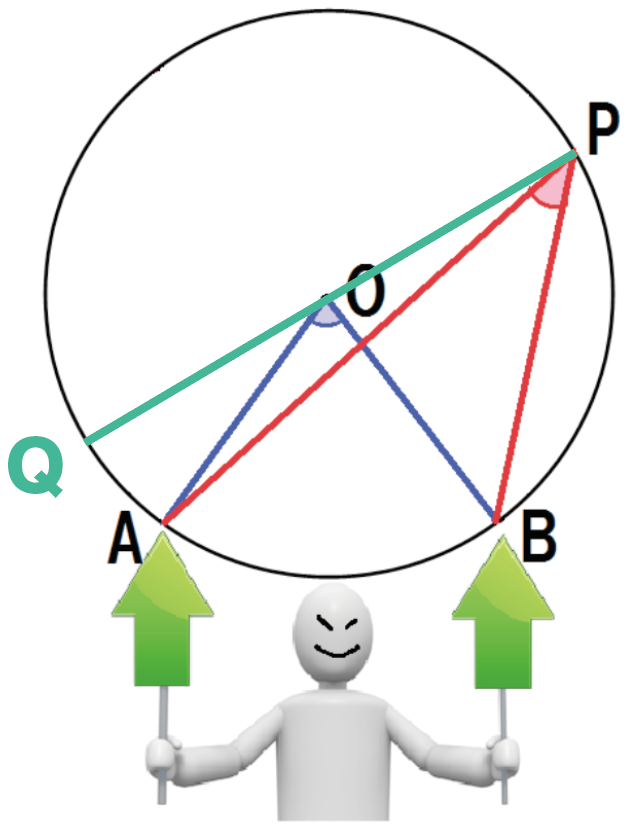
ややこしいから、目を皿のようにして見とけよ!

同じように図形を分解して、見やすくしてみるね。
重なりをバラバラにして、
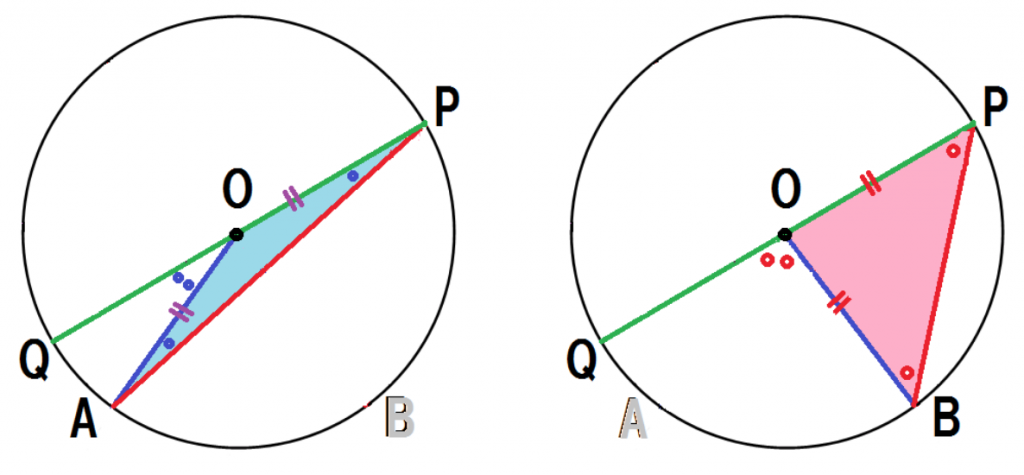
左と右でそれぞれ分けて考えてみるよ。
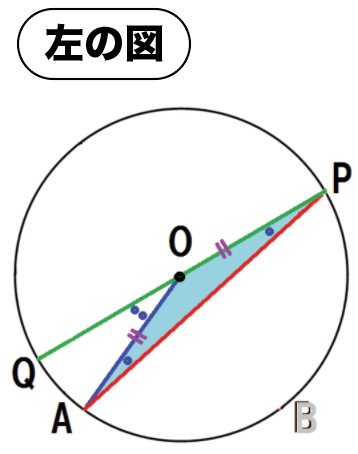
OP・OAはそれぞれ円Oの半径だから、
OP = OA
よって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)
三角形の外角の定理より、
∠AOQ = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APQ = 1/2∠AOQ・・・(3)

OP・OBはそれぞれ円Oの半径だから、
OP = OB
よって、△OPBはOP = OBの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OBP = ∠OPB ・・・ (4)
三角形の外角の定理より、
∠BOQ = ∠OBP + ∠OPB・・・(5)
(4)、(5)より、
∠BPQ = 1/2∠BOQ・・・(6)
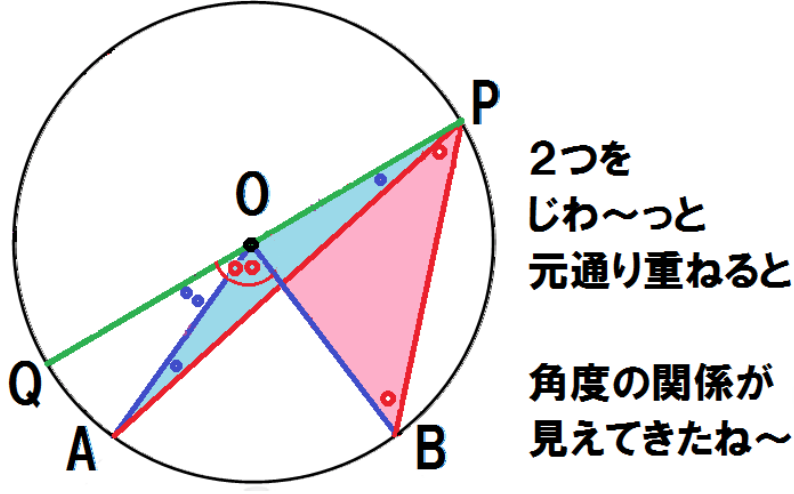
(3)・(6)より、
∠BPQ -∠APQ = 1/2∠BOQ – 1/2∠AOQ
よって、
∠APB = 1/2∠AOB
よって、
円周角∠APB は∠AOBの半分である。
円周角の定理の証明は3パターンで楽勝!!
円周角の定理の証明はどうだったかな??
つぎの3パターンの証明ができればよかったよね?
- 点 PがOB上にあるとき
- 中心Oが∠APBの内側にあるとき
- 中心 Oが∠APBの外側にあるとき
3パターンとも証明しちゃったんだから使いホーダイ。

円周角の定理を心気なくガシガシ使っていこう。
じゃあな。
Dr.リード


